面面平行的判定与性质
图片预览




文档简介
(共36张PPT)
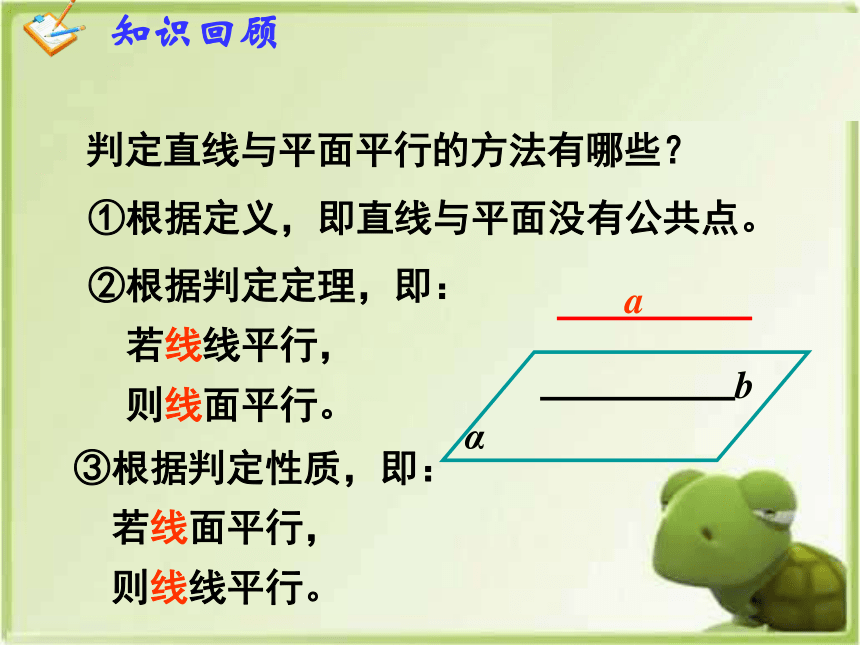
②根据判定定理,即:
若线线平行,
则线面平行。
知识回顾
判定直线与平面平行的方法有哪些?
a
b
α
①根据定义,即直线与平面没有公共点。
③根据判定性质,即:
若线面平行,
则线线平行。
知识回顾
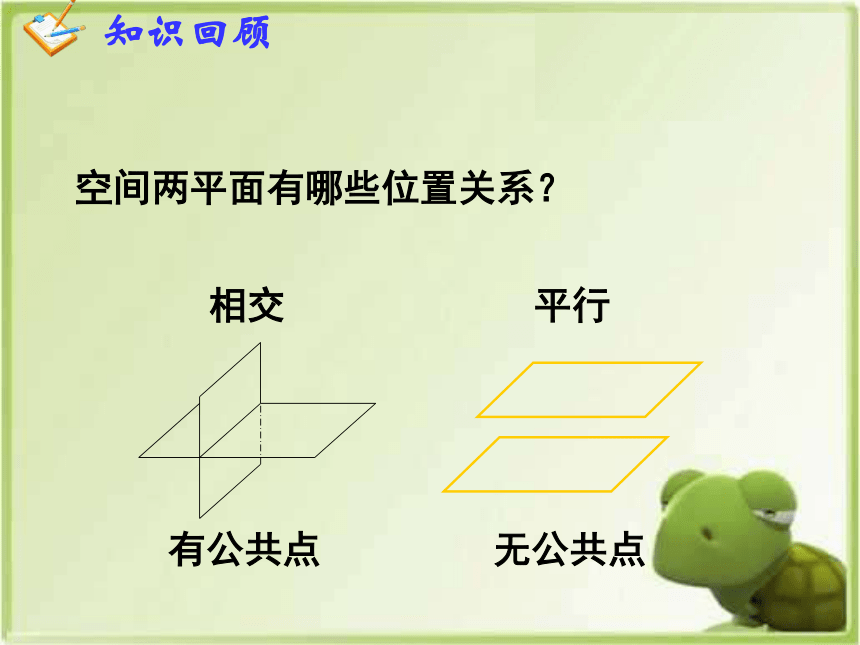
空间两平面有哪些位置关系?
相交
平行
有公共点
无公共点
平面与平面平行的判定
定义:如果两个平面没有公共点,那么这
两个平面互相平行,也叫做平行平面
平面α平行于平面β ,记作α∥β
但是,平面无限延展,用定义判定平面与平面平行的可行性不大。
思考:
反之,若α中所有直线都平行β ,则α∥β
启示
两个平面平行的问题,可以转化为一个平面内的直线与另一个平面平行的问题。
若平面α∥β,则α中所有直线都平行β
新知探究
;
!
线面平行
面面平行
转 化
无限
有限
转 化
平面α内有一条直线 a 平行平面β,
则α∥ β 吗 请举例说明。
问题1
问题2
平面α内有两条直线 a , b 平行平面
β, 则α∥ β 吗 请举例说明。
探究:
二、新知探究
模型1
α
β
a
α// β
α
α
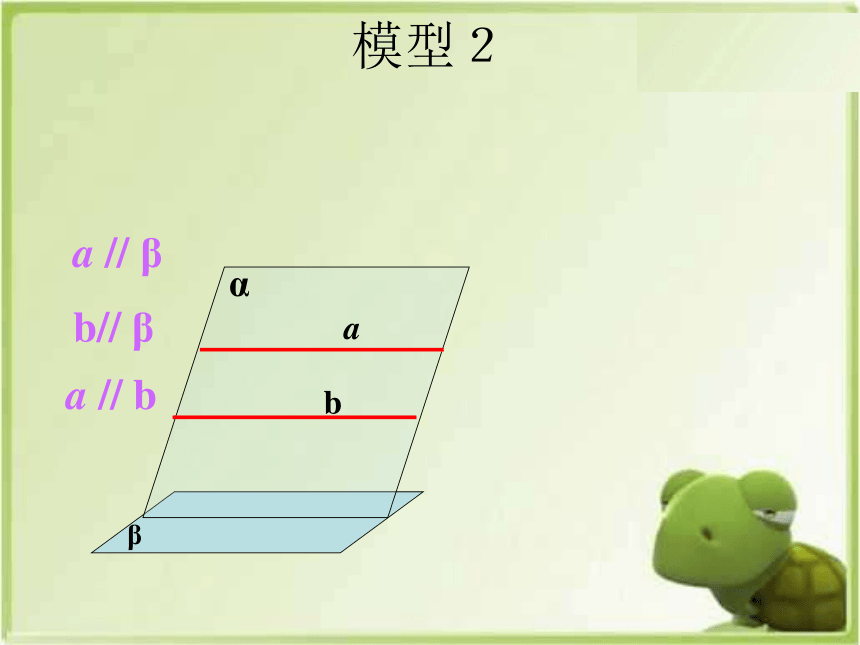
模型2
a // β
a
b
α
b// β
β
a // b
直观
感受
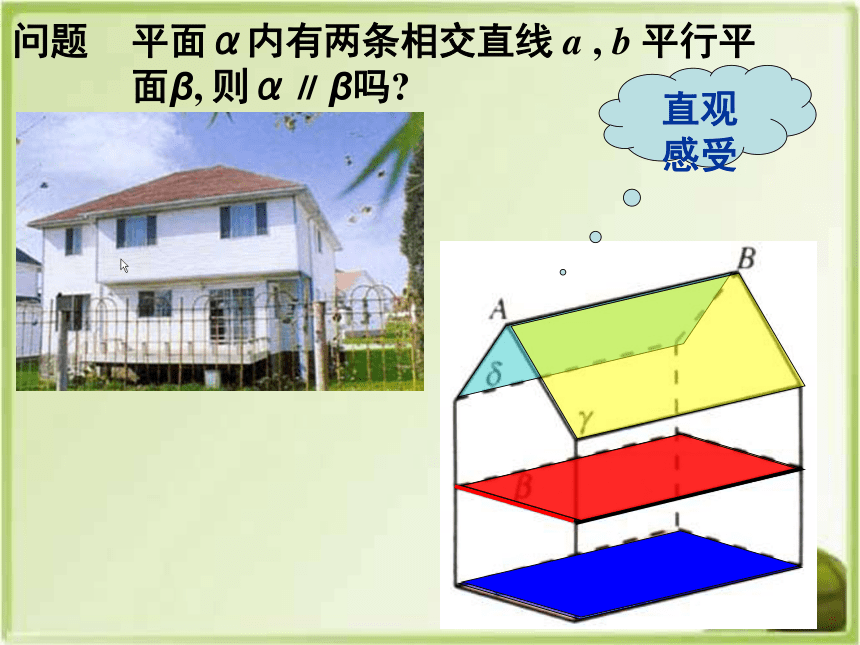
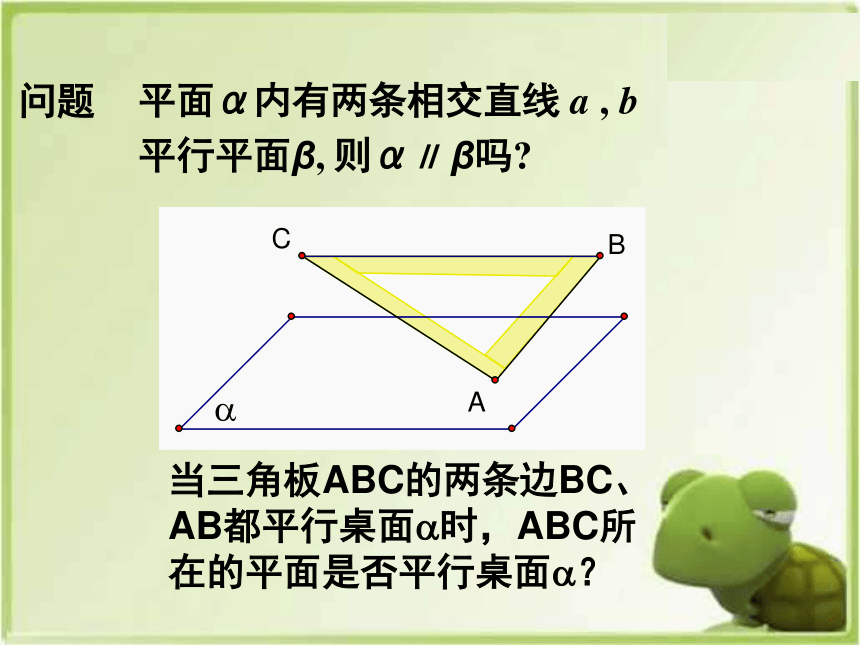
问题
平面α内有两条相交直线 a , b 平行平面β, 则α∥ β吗
当三角板ABC的两条边BC、AB都平行桌面 时,ABC所在的平面是否平行桌面 ?
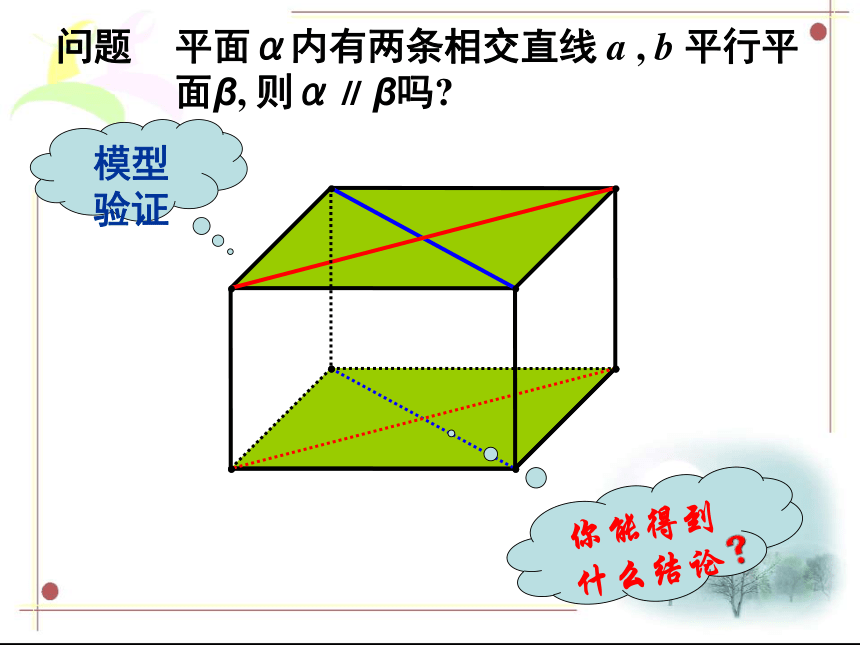
问题
平面α内有两条相交直线 a , b
平行平面β, 则α∥ β吗
模型
验证
问题
平面α内有两条相交直线 a , b 平行平面β, 则α∥ β吗
你能得到什么结论
a , b
a b=P
a //
b //
//
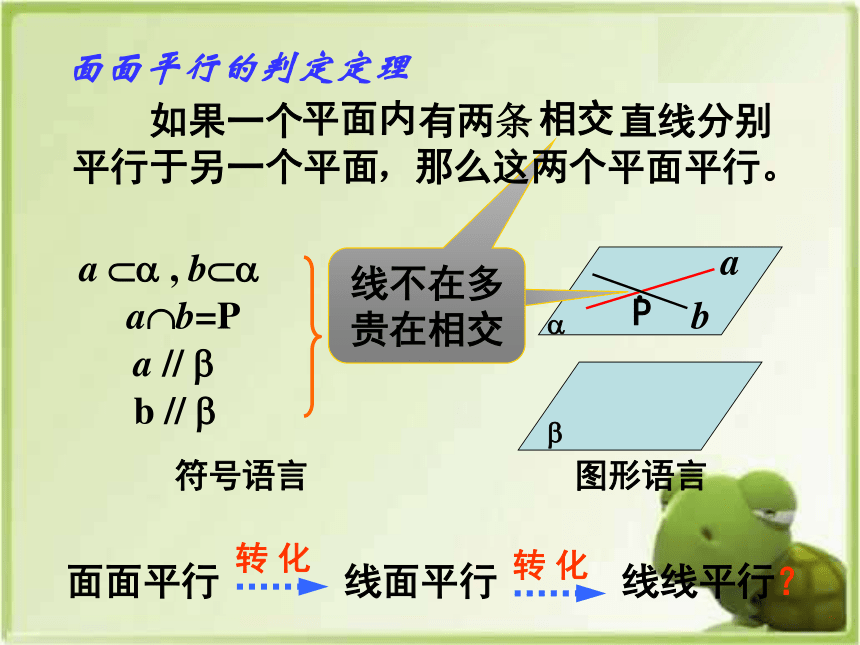
面面平行的判定定理
符号语言
线不在多
贵在相交
面面平行
线面平行
线线平行?
a
b
图形语言
如果一个 有两条 直线分别
于另一个平面
相交
,那么这两个平面平行。
P
转 化
转 化
平面内
平行
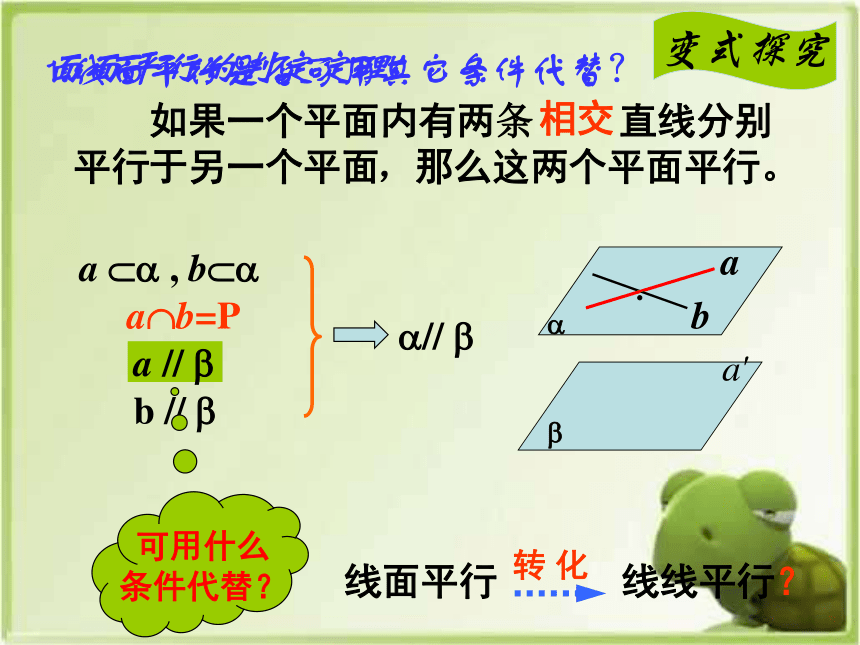
1.线面平行是否可用其它条件代替?
a , b
a b=P
a //
b //
//
面面平行的判定定理
a
b
如果一个平面内有两条 直线分别
平行于另一个平面
相交
,那么这两个平面平行。
可用什么
条件代替?
变式探究
线面平行
线线平行?
转 化
a //
a , b
a b=P
b //
//
a
b
a∥ ,
如果一个平面内有两条 直线分别
平行于另一个平面
相交
,那么这两个平面平行。
1.线面平行是否可用其它条件代替?
变式探究
线面平行
线线平行?
转 化
a , b
a b=P
b //
//
a
b
图形语言
a∥ ,
b∥ ,
如果一个平面内有两条 直线分别
平行于另一个平面
相交
,那么这两个平面平行。
1.线面平行是否可用其它条件代替?
变式探究
符号语言
线面平行
线线平行?
转 化
b∥ ,
a , b
a b=P
//
a
b
图形语言
a∥ ,
如果一个平面内有两条 直线分别
平行于另一个平面
相交
,那么这两个平面平行。
,那么这两个平面平行。
内的两直线
1.线面平行是否可用其它条件代替?
变式探究
推论
符号语言
例题解析
例 : 判断下列结论是否正确:
1.若m α, n α, m∥β, n∥β, 则α∥β
2.若α内有无数条直线平行于β, 则α∥β
3.若α内任意直线都平行于β, 则α∥β
4.若m // n,m//α,m //β,n//α,n//β,则α//β
5.若α//γ,β//γ,则α//β
例二
已知 正方体 ,求证:
1
1
1
1
D
A
B
D
C
B
C
A
分析:
在四边形ABC1D1中,AB∥C1D1且AB=C1D1故四边形ABC1D1为平行四边形。
即AD1∥BC1
证明:
∵ABCD-A1B1C1D1是正方体,
∴D1C1//A1B1,D1C1=A1B1,
AB//A1B1,AB=A1B1,
∴D1C1//AB,D1C1=AB,
∴D1C1BA为平行四边形,
∴ D1A//C1B,
又D1A 平面C1BD,
C1B 平面C1BD,
∴D1A//平面C1BD。
1
1
1
1
D
A
B
D
C
B
C
A
同理D1B1//平面C1BD,
又D1A D1B1=D1,
D1A 平面AB1D1 ,
D1B1 平面AB1D1,
∴平面AB1D1//平面C1BD。
1
1
1
1
D
A
B
D
C
B
C
A
已知正方体ABCD-A1B1C1D1,P、Q、R分别为A1A、AB、AD的中点 .求证:平面PQR∥平面CB1D1。
P
Q
R
连结A1B,BD。
因为PQ∥ A1B且A1B ∥CD1。
故PQ∥CD1。
同理可得,RQ//B1D1。
所以平面PQR∥平面CB1D1。
变式
正方体中面与面的平行关系有还有这些:
小结
平面与平面平行的判定定理
一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
定理的推论
如果一个平面内有两条相交直线分别平行于
另一个平面内的两条直线,那么这两个平面平行
平面与平面平行的性质
如果两个平面平行,那么一平面中的直线与另一平面有什么位置关系?
由于平面A'C'平行于平面AC,不可能有交点,所以直线A'C'与平面AC平行。
如果两个平面平行,那么一个平面内的直线与另一个平面的直线具有什么位置关系?
由于平面A'C'平行于平面AC,不可能有交点,所以直线A'C'与平面AC内直线的位置关系只可能是平行或异面.如A'C'与AC平行,与AB或BC异面。
如何找到在平面AC中与直线A'C'平行的直线?
只要与直线A'C'在一个平面内即可.过直线A'C'做一个平面与平面AC相交,则交线与直线A'C'平行。
例五
a
b
α
β
γ
如图,已知平面α,β,γ,满足α//β,α∩γ=a,β∩γ=b,求证:a//b。
证明:
所以a,b没有公共点
平面与平面平行的性质定理
如果两个平行平面同时和第三个平面相交,那么它们的交线平行
面面平行→线线平行
符号表示:
1. 若两个平面互相平行,则其中一个平面中的直线必平行于另一个平面;
2. 平行于同一平面的两平面平行;
3. 过平面外一点有且只有一个平面与这个平面平行;
4. 夹在两平行平面间的平行线段相等。
由两个平面平行可以得到哪些结论呢?
证明:因为AB//CD,所以过AB,CD可作平面γ,且平面γ与平面α和β分别相交AC和BD
因为α//β,
所以BD//AC
因此,四边形ABCD是平行四边形
所以AB=CD
例六
A
C
B
D
已知:如图α//β,AB//CD,且
求证:AB=CD
小结
面面平行判定定理:
如果一个平面内有两条相交直线分别平行于
另一个平面,那么这两个平面平行。
推论:
如果一个平面内有两条相交直线分别平行于
另一个平面内的两条直线,那么这两个平面平行
面面平行性质定理:
如果两个平行平面同时与第三个平面相交,那么它们的交线平行。
线面平行 面面平行
面面平行 线线平行
②根据判定定理,即:
若线线平行,
则线面平行。
知识回顾
判定直线与平面平行的方法有哪些?
a
b
α
①根据定义,即直线与平面没有公共点。
③根据判定性质,即:
若线面平行,
则线线平行。
知识回顾
空间两平面有哪些位置关系?
相交
平行
有公共点
无公共点
平面与平面平行的判定
定义:如果两个平面没有公共点,那么这
两个平面互相平行,也叫做平行平面
平面α平行于平面β ,记作α∥β
但是,平面无限延展,用定义判定平面与平面平行的可行性不大。
思考:
反之,若α中所有直线都平行β ,则α∥β
启示
两个平面平行的问题,可以转化为一个平面内的直线与另一个平面平行的问题。
若平面α∥β,则α中所有直线都平行β
新知探究
;
!
线面平行
面面平行
转 化
无限
有限
转 化
平面α内有一条直线 a 平行平面β,
则α∥ β 吗 请举例说明。
问题1
问题2
平面α内有两条直线 a , b 平行平面
β, 则α∥ β 吗 请举例说明。
探究:
二、新知探究
模型1
α
β
a
α// β
α
α
模型2
a // β
a
b
α
b// β
β
a // b
直观
感受
问题
平面α内有两条相交直线 a , b 平行平面β, 则α∥ β吗
当三角板ABC的两条边BC、AB都平行桌面 时,ABC所在的平面是否平行桌面 ?
问题
平面α内有两条相交直线 a , b
平行平面β, 则α∥ β吗
模型
验证
问题
平面α内有两条相交直线 a , b 平行平面β, 则α∥ β吗
你能得到什么结论
a , b
a b=P
a //
b //
//
面面平行的判定定理
符号语言
线不在多
贵在相交
面面平行
线面平行
线线平行?
a
b
图形语言
如果一个 有两条 直线分别
于另一个平面
相交
,那么这两个平面平行。
P
转 化
转 化
平面内
平行
1.线面平行是否可用其它条件代替?
a , b
a b=P
a //
b //
//
面面平行的判定定理
a
b
如果一个平面内有两条 直线分别
平行于另一个平面
相交
,那么这两个平面平行。
可用什么
条件代替?
变式探究
线面平行
线线平行?
转 化
a //
a , b
a b=P
b //
//
a
b
a∥ ,
如果一个平面内有两条 直线分别
平行于另一个平面
相交
,那么这两个平面平行。
1.线面平行是否可用其它条件代替?
变式探究
线面平行
线线平行?
转 化
a , b
a b=P
b //
//
a
b
图形语言
a∥ ,
b∥ ,
如果一个平面内有两条 直线分别
平行于另一个平面
相交
,那么这两个平面平行。
1.线面平行是否可用其它条件代替?
变式探究
符号语言
线面平行
线线平行?
转 化
b∥ ,
a , b
a b=P
//
a
b
图形语言
a∥ ,
如果一个平面内有两条 直线分别
平行于另一个平面
相交
,那么这两个平面平行。
,那么这两个平面平行。
内的两直线
1.线面平行是否可用其它条件代替?
变式探究
推论
符号语言
例题解析
例 : 判断下列结论是否正确:
1.若m α, n α, m∥β, n∥β, 则α∥β
2.若α内有无数条直线平行于β, 则α∥β
3.若α内任意直线都平行于β, 则α∥β
4.若m // n,m//α,m //β,n//α,n//β,则α//β
5.若α//γ,β//γ,则α//β
例二
已知 正方体 ,求证:
1
1
1
1
D
A
B
D
C
B
C
A
分析:
在四边形ABC1D1中,AB∥C1D1且AB=C1D1故四边形ABC1D1为平行四边形。
即AD1∥BC1
证明:
∵ABCD-A1B1C1D1是正方体,
∴D1C1//A1B1,D1C1=A1B1,
AB//A1B1,AB=A1B1,
∴D1C1//AB,D1C1=AB,
∴D1C1BA为平行四边形,
∴ D1A//C1B,
又D1A 平面C1BD,
C1B 平面C1BD,
∴D1A//平面C1BD。
1
1
1
1
D
A
B
D
C
B
C
A
同理D1B1//平面C1BD,
又D1A D1B1=D1,
D1A 平面AB1D1 ,
D1B1 平面AB1D1,
∴平面AB1D1//平面C1BD。
1
1
1
1
D
A
B
D
C
B
C
A
已知正方体ABCD-A1B1C1D1,P、Q、R分别为A1A、AB、AD的中点 .求证:平面PQR∥平面CB1D1。
P
Q
R
连结A1B,BD。
因为PQ∥ A1B且A1B ∥CD1。
故PQ∥CD1。
同理可得,RQ//B1D1。
所以平面PQR∥平面CB1D1。
变式
正方体中面与面的平行关系有还有这些:
小结
平面与平面平行的判定定理
一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
定理的推论
如果一个平面内有两条相交直线分别平行于
另一个平面内的两条直线,那么这两个平面平行
平面与平面平行的性质
如果两个平面平行,那么一平面中的直线与另一平面有什么位置关系?
由于平面A'C'平行于平面AC,不可能有交点,所以直线A'C'与平面AC平行。
如果两个平面平行,那么一个平面内的直线与另一个平面的直线具有什么位置关系?
由于平面A'C'平行于平面AC,不可能有交点,所以直线A'C'与平面AC内直线的位置关系只可能是平行或异面.如A'C'与AC平行,与AB或BC异面。
如何找到在平面AC中与直线A'C'平行的直线?
只要与直线A'C'在一个平面内即可.过直线A'C'做一个平面与平面AC相交,则交线与直线A'C'平行。
例五
a
b
α
β
γ
如图,已知平面α,β,γ,满足α//β,α∩γ=a,β∩γ=b,求证:a//b。
证明:
所以a,b没有公共点
平面与平面平行的性质定理
如果两个平行平面同时和第三个平面相交,那么它们的交线平行
面面平行→线线平行
符号表示:
1. 若两个平面互相平行,则其中一个平面中的直线必平行于另一个平面;
2. 平行于同一平面的两平面平行;
3. 过平面外一点有且只有一个平面与这个平面平行;
4. 夹在两平行平面间的平行线段相等。
由两个平面平行可以得到哪些结论呢?
证明:因为AB//CD,所以过AB,CD可作平面γ,且平面γ与平面α和β分别相交AC和BD
因为α//β,
所以BD//AC
因此,四边形ABCD是平行四边形
所以AB=CD
例六
A
C
B
D
已知:如图α//β,AB//CD,且
求证:AB=CD
小结
面面平行判定定理:
如果一个平面内有两条相交直线分别平行于
另一个平面,那么这两个平面平行。
推论:
如果一个平面内有两条相交直线分别平行于
另一个平面内的两条直线,那么这两个平面平行
面面平行性质定理:
如果两个平行平面同时与第三个平面相交,那么它们的交线平行。
线面平行 面面平行
面面平行 线线平行
