2021-2022学年人教版数学八年级上册11.2.2 三角形外角 课件(24张)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册11.2.2 三角形外角 课件(24张) |

|
|
| 格式 | zip | ||
| 文件大小 | 632.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 00:00:00 | ||
图片预览





文档简介
(共24张PPT)
7.2.2三角形的外角
2、在ABC中,
(1)∠C=90°,∠A=30 ° ,则∠B= ;
(2)∠A=50 ° ,∠B=∠C,则∠B= .
1、三角形三个内角的和等于多少度?
知识回顾
3、在△ABC中,
∠A:∠B:∠C=2:3:4则∠A= ,
∠B= ∠C=
40°
60°
80°
65°
60°
三角形的内角和等于180度
A
B
C
D
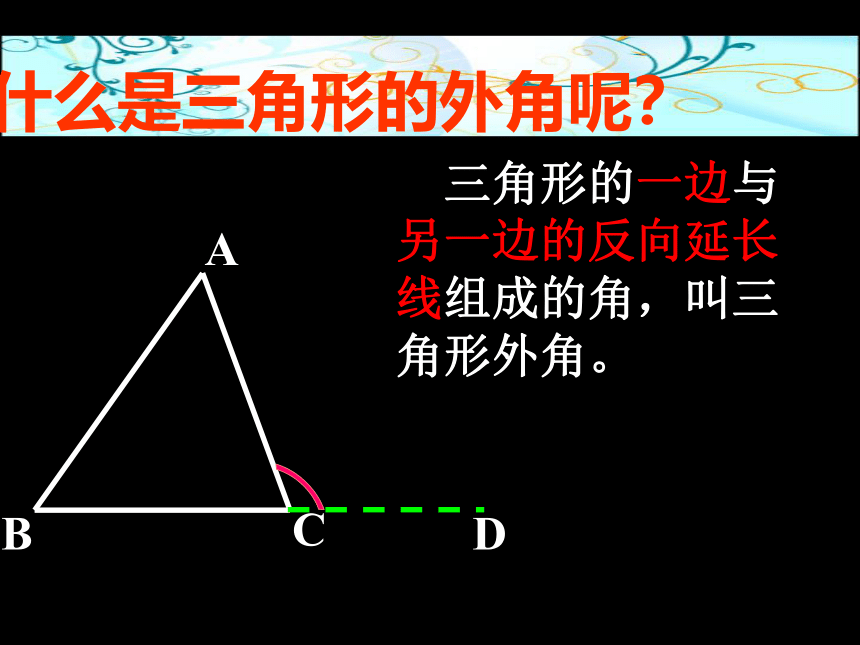
什么是三角形的外角呢?
三角形的一边与另一边的反向延长线组成的角,叫三角形外角。
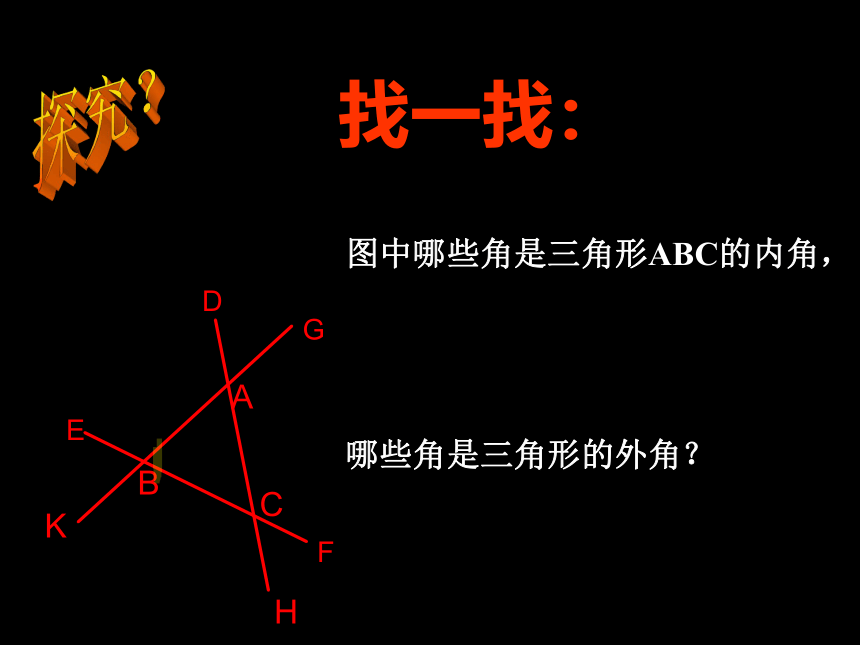
找一找:
探究?
图中哪些角是三角形ABC的内角,
哪些角是三角形的外角?
D
K
H
A
C
B
G
F
E
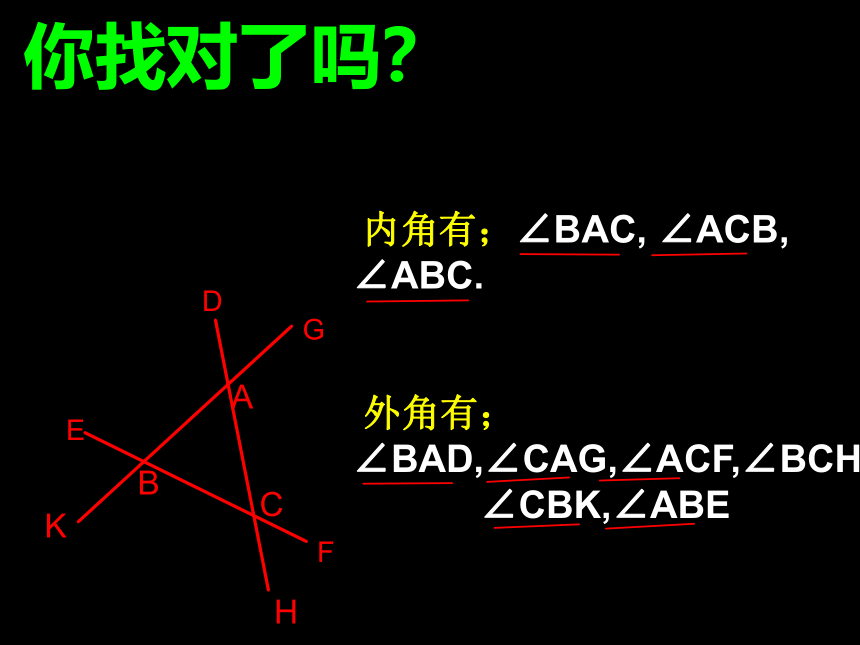
你找对了吗?
内角有;∠BAC, ∠ACB, ∠ABC.
外角有;∠BAD,∠CAG,∠ACF,∠BCH,
∠CBK,∠ABE
D
K
H
A
C
B
G
F
E
想一想:
三角形的外角在构成上有什么特点
三角形共有几个外角?
努力哦
你理解了吗?
三角形的外角有什么特点?
外角的顶点在三角形的顶点上。
外角的一边是原三角形的一边,另一边是三角形相邻那条边的延长线。
外角与相邻的内角是对邻补角。
三角形共有几个外角?
三角形同一顶点上两个外角,这两个外角互为对顶角。
三角形有三个顶点,每个顶点上有二个外角,因此共有6个外角 ,但数学上一般只研究顶点上的一个外角。
A
B
C
D
E
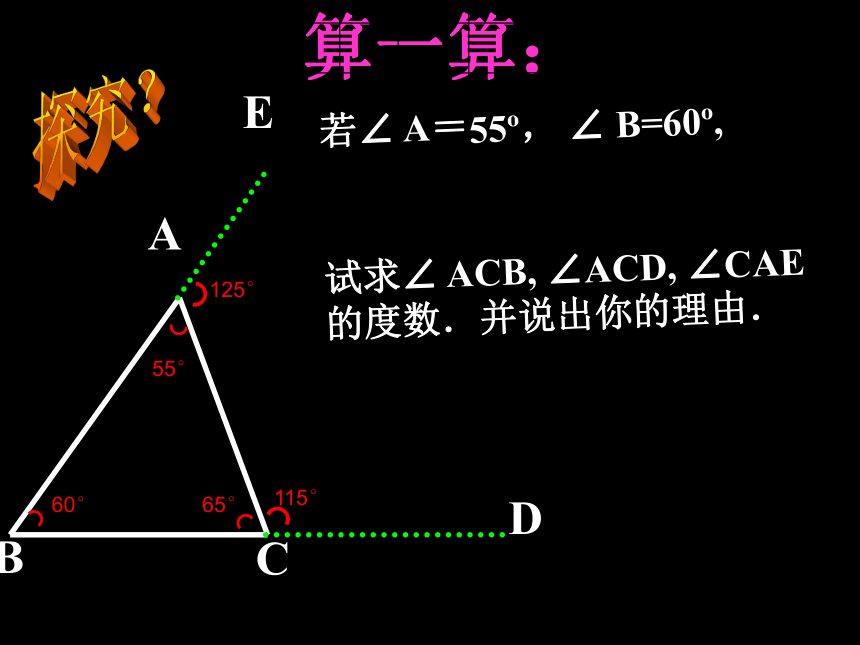
算一算:
若∠ A=
55 , ∠ B=60 ,
试求∠ ACB, ∠ACD, ∠CAE
的度数.并说出你的理由.
探究?
⌒
⌒
⌒
⌒
⌒
115°
60°
65°
55°
125°
你发现∠ACD, ∠ CAE与三角形的内角之间有怎样的数量关系呢?
∠ACD=∠BAC+∠B ∠CAE=∠B+∠ACD
想一想:
三角形的一个外角等于与它不相邻的两个内角的和。
三角形外角和定理:
求下列各图中∠1的度数。
30°
60°
1
35°
120°
1
45°
50°
1
∠1=
∠1=
∠1=
90
85
95
填一填:
∠ACD ∠A (<、>);
∠ACD ∠B (<、>)
三角形外角定理的推论:三角形的一个外角大于任何一个与它不相邻的内角。
D
A
C
B
>
>
你选什么 ?
把图中∠1、 ∠2、 ∠3按由大到小的顺序排列
B
3
2
1
A
C
D
E
∠1
∠2
∠3
>
>
A
B
C
1
2
3
∠1+∠2 +∠3 =
从哪些途径探究这个结果
议一议
探究三角形外角和有什么特点?
A
B
C
1
2
3
∠2+ ∠ABC=180°
∠3+ ∠ACB=180°
由 + + 得到:
∠1+ ∠2+ ∠3+ ∠BAC+ ∠ABC+∠ACB=540°
而∠BAC+ ∠ABC+∠ACB=180°
∠1+ ∠2+ ∠3=360°
∠1+ ∠BAC=180°
解法一:
三角形外角和定理:
三角形的外角和等于360°
解法二:过A作AD平行于BC
∴ ∠3= ∠4
B
C
1
2
3
4
A
∴ ∠2= ∠BAD
∴ ∠1+ ∠2+ ∠3= ∠1+ ∠BAD+ ∠4=360°
两直线平行,同位角相等
D
判断题:
1、三角形的外角和是指三角形所有外角的和。( )
2、三角形的外角和等于它内角和的2倍。( )
3、三角形的一个外角等于两个内角的和。( )
4、三角形的一个外角等于与它不相邻的两个内角的和。( )
5、三角形的一个外角大于任何一个内角。( )
6、三角形的一个内角小于任何一个与它不相邻的外角。( )
练一练
算一算
例1:如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
问:(1)中为什么∠ADC=∠B+∠BAD?
(2)中求∠C的度数还有其他方法吗?
A
B
C
D
80°
70°
40
40
⌒
∠A+∠B+∠C+∠D+∠E+∠F= .
A
D
E
C
F
B
1
2
3
360°
N
P
M
课堂练习:
例1:如图
A
B
C
D
E
例2: 求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数
⌒
F
G
⌒
∠B+ ∠D= ∠EGF
∠EGF + ∠EFG + ∠E = 180°
∠A+ ∠C= ∠EFG
解:因为
所以
∠A+ ∠B+ ∠C+ ∠D+ ∠E= 180°
课外练习
1.已知图中∠A、 ∠B、 ∠C分别为80°, 20° , 30° ,求∠1的度数
B
3
2
1
A
C
D
E
2.(如图)试计算∠BOC的度数.
90
30
20
A
B
C
O
D
⌒
110°
如图,在直角△ABC中,CD是斜边AB上的高,∠BCD=35°,
求∠A与∠EBC的度数.
A
B
C
D
E
∟
⌒
35°
⌒
⌒
比一比,谁最先算出来!
小结
1、三角形外角的两条性质
① 三角形的一个外角等于与它不相邻
的两个内角的和。
②三角形的一个外角大于任何一个与它
不相邻的内角。
任何三角形的外角和是360
今天你收获了什么?
祝你学习进步
7.2.2三角形的外角
2、在ABC中,
(1)∠C=90°,∠A=30 ° ,则∠B= ;
(2)∠A=50 ° ,∠B=∠C,则∠B= .
1、三角形三个内角的和等于多少度?
知识回顾
3、在△ABC中,
∠A:∠B:∠C=2:3:4则∠A= ,
∠B= ∠C=
40°
60°
80°
65°
60°
三角形的内角和等于180度
A
B
C
D
什么是三角形的外角呢?
三角形的一边与另一边的反向延长线组成的角,叫三角形外角。
找一找:
探究?
图中哪些角是三角形ABC的内角,
哪些角是三角形的外角?
D
K
H
A
C
B
G
F
E
你找对了吗?
内角有;∠BAC, ∠ACB, ∠ABC.
外角有;∠BAD,∠CAG,∠ACF,∠BCH,
∠CBK,∠ABE
D
K
H
A
C
B
G
F
E
想一想:
三角形的外角在构成上有什么特点
三角形共有几个外角?
努力哦
你理解了吗?
三角形的外角有什么特点?
外角的顶点在三角形的顶点上。
外角的一边是原三角形的一边,另一边是三角形相邻那条边的延长线。
外角与相邻的内角是对邻补角。
三角形共有几个外角?
三角形同一顶点上两个外角,这两个外角互为对顶角。
三角形有三个顶点,每个顶点上有二个外角,因此共有6个外角 ,但数学上一般只研究顶点上的一个外角。
A
B
C
D
E
算一算:
若∠ A=
55 , ∠ B=60 ,
试求∠ ACB, ∠ACD, ∠CAE
的度数.并说出你的理由.
探究?
⌒
⌒
⌒
⌒
⌒
115°
60°
65°
55°
125°
你发现∠ACD, ∠ CAE与三角形的内角之间有怎样的数量关系呢?
∠ACD=∠BAC+∠B ∠CAE=∠B+∠ACD
想一想:
三角形的一个外角等于与它不相邻的两个内角的和。
三角形外角和定理:
求下列各图中∠1的度数。
30°
60°
1
35°
120°
1
45°
50°
1
∠1=
∠1=
∠1=
90
85
95
填一填:
∠ACD ∠A (<、>);
∠ACD ∠B (<、>)
三角形外角定理的推论:三角形的一个外角大于任何一个与它不相邻的内角。
D
A
C
B
>
>
你选什么 ?
把图中∠1、 ∠2、 ∠3按由大到小的顺序排列
B
3
2
1
A
C
D
E
∠1
∠2
∠3
>
>
A
B
C
1
2
3
∠1+∠2 +∠3 =
从哪些途径探究这个结果
议一议
探究三角形外角和有什么特点?
A
B
C
1
2
3
∠2+ ∠ABC=180°
∠3+ ∠ACB=180°
由 + + 得到:
∠1+ ∠2+ ∠3+ ∠BAC+ ∠ABC+∠ACB=540°
而∠BAC+ ∠ABC+∠ACB=180°
∠1+ ∠2+ ∠3=360°
∠1+ ∠BAC=180°
解法一:
三角形外角和定理:
三角形的外角和等于360°
解法二:过A作AD平行于BC
∴ ∠3= ∠4
B
C
1
2
3
4
A
∴ ∠2= ∠BAD
∴ ∠1+ ∠2+ ∠3= ∠1+ ∠BAD+ ∠4=360°
两直线平行,同位角相等
D
判断题:
1、三角形的外角和是指三角形所有外角的和。( )
2、三角形的外角和等于它内角和的2倍。( )
3、三角形的一个外角等于两个内角的和。( )
4、三角形的一个外角等于与它不相邻的两个内角的和。( )
5、三角形的一个外角大于任何一个内角。( )
6、三角形的一个内角小于任何一个与它不相邻的外角。( )
练一练
算一算
例1:如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
问:(1)中为什么∠ADC=∠B+∠BAD?
(2)中求∠C的度数还有其他方法吗?
A
B
C
D
80°
70°
40
40
⌒
∠A+∠B+∠C+∠D+∠E+∠F= .
A
D
E
C
F
B
1
2
3
360°
N
P
M
课堂练习:
例1:如图
A
B
C
D
E
例2: 求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数
⌒
F
G
⌒
∠B+ ∠D= ∠EGF
∠EGF + ∠EFG + ∠E = 180°
∠A+ ∠C= ∠EFG
解:因为
所以
∠A+ ∠B+ ∠C+ ∠D+ ∠E= 180°
课外练习
1.已知图中∠A、 ∠B、 ∠C分别为80°, 20° , 30° ,求∠1的度数
B
3
2
1
A
C
D
E
2.(如图)试计算∠BOC的度数.
90
30
20
A
B
C
O
D
⌒
110°
如图,在直角△ABC中,CD是斜边AB上的高,∠BCD=35°,
求∠A与∠EBC的度数.
A
B
C
D
E
∟
⌒
35°
⌒
⌒
比一比,谁最先算出来!
小结
1、三角形外角的两条性质
① 三角形的一个外角等于与它不相邻
的两个内角的和。
②三角形的一个外角大于任何一个与它
不相邻的内角。
任何三角形的外角和是360
今天你收获了什么?
祝你学习进步
