2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册1.4.1 用空间向量研究直线、平面的位置关系课件(共42张PPT)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册1.4.1 用空间向量研究直线、平面的位置关系课件(共42张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 20:38:27 | ||
图片预览








文档简介
(共42张PPT)
1.4 空间向量的应用
1.4.1 用空间向量研究直线、平面的位置关系
我们已经把向量从平面推广到空间,并利用空间向量解决了一些有关空间位置关系和度量的问题。我们发现,建立空间向量与几何要素的对应关系是利用空间向量解决立体几何问题的关键.本节我们进一步运用空间向量研究立体几何中有关直线、平面的位置关系和度量问题.
立体几何问题
平面向量
推广
空间向量
研究的基本对象是点、直线、平面以及由它们组成的空间图形
研究
l
A
P
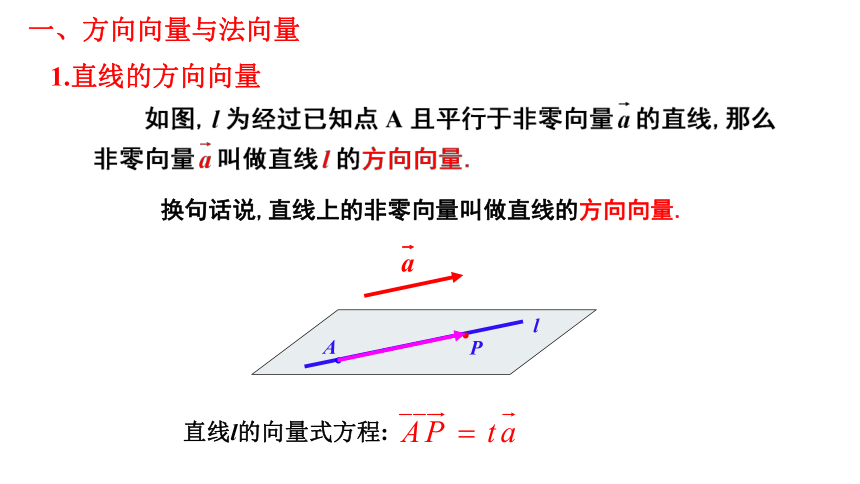
1.直线的方向向量
直线l的向量式方程:
换句话说,直线上的非零向量叫做直线的方向向量.
一、方向向量与法向量
O
我们知道,点、直线和平面是空间的基本图形,点、线段和平面图形等是组成空间几何体的基本元素,因此,为了用空间向量解决立体几何问题,首先要用向量表示空间中的点、直线和平面.
1. 空间中点、直线和平面的向量表示
思考1 如何用向量表示空间中的一个点
P
如图示,在空间中,我们取一定点O作为基点,那么空间中任意一点P就可以用向量 来表示,我们把向量 称为点P的位置向量.
直线的方向向量:
换句话说,直线上的非零向量叫做直线的方向向量.
l
A
如图,l为经过已知点A且平行于非零向量 的直线,那么非零向量 叫做直线l的方向向量.
用向量表示直线l,就是要利用点A和直线l的方向向量表示直线上的任意一点.
思考2 我们知道,空间中给定一个点A和一个方向就能唯一确定一条直线l. 如何用向量表示直线l
A
P
l
B
如图示, 是直线l的方向向量,在直线l上取 设P是直线l上的任意一点,由向量共线的条件可知,点P在直线l上的充要条件是存在实数t,使得
进一步地,如图示,取定空间中的任意一点O,可以得到点P在直线l上的充要条件是存在实数t,使
O
将 带入①式,得
①式和②式都称为空间直线的向量表示式. 由此可知,空间任意直线由直线上一点及直线的方向向量唯一确定.
思考3 一个定点和两个定方向能否确定一个平面 进一步地,一个定点和一个定方向能否确定一个平面 如果能确定,如何用向量表示这个平面
我们知道,平面α可以由α内两条相交直线确定. 如图示,设两条直线相交于点O,它们的方向向量分别为 和 ,P为平面α内任意一点,由平面向量基本定理可知,存在唯一 的有序实数对(x, y),使得
这样,点O与向量 不仅可以确定平面α,还可以具体表示出α内的任意一点. 这种表示在解决几何问题时有重要作用.
α
O
P
进一步地, 如右图示, 取定空间任意一点O, 可以得到, 空间一点P位于平面ABC内的充要条件是存在实数x, y, 使
我们把③式称为空间平面ABC的向量表示式. 由此可知,空间中任意平面由空间一点及两个不共线向量唯一确定.
α
A
P
C
B
O
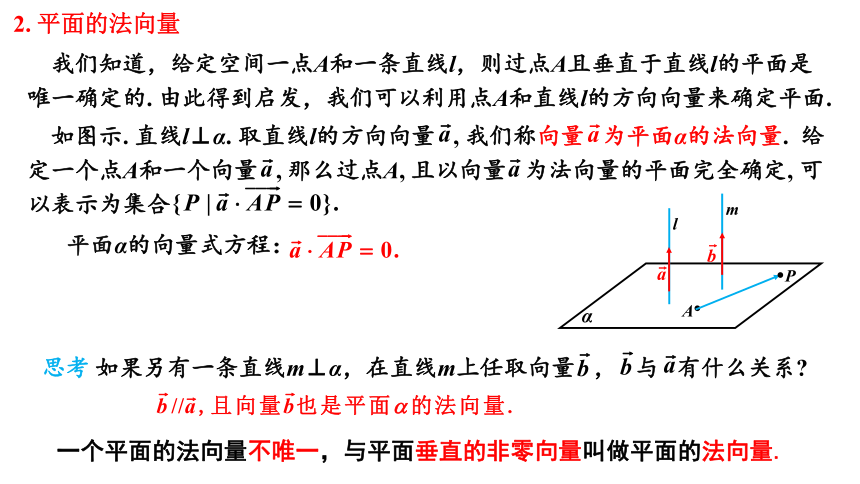
2. 平面的法向量
我们知道,给定空间一点A和一条直线l,则过点A且垂直于直线l的平面是唯一确定的. 由此得到启发,我们可以利用点A和直线l的方向向量来确定平面.
如图示. 直线l⊥α. 取直线l的方向向量 , 我们称向量 为平面α的法向量. 给定一个点A和一个向量 , 那么过点A, 且以向量 为法向量的平面完全确定, 可以表示为集合
α
A
l
思考 如果另有一条直线m⊥α,在直线m上任取向量 , 与 有什么关系
m
一个平面的法向量不唯一,与平面垂直的非零向量叫做平面的法向量.
P
平面α的向量式方程:
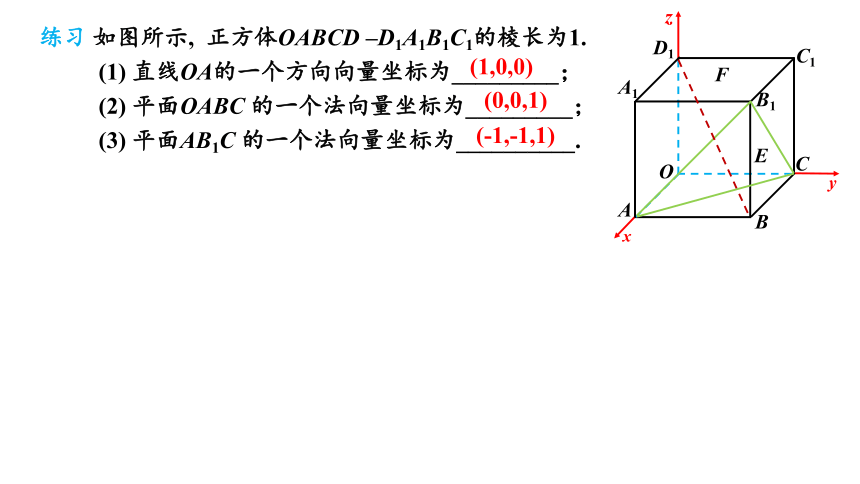
练习 如图所示, 正方体OABCD –D1A1B1C1的棱长为1.
(1) 直线OA的一个方向向量坐标为_________;
(2) 平面OABC 的一个法向量坐标为_________;
(3) 平面AB1C 的一个法向量坐标为__________.
(-1,-1,1)
(0,0,1)
(1,0,0)
A
O
C
B
A1
D1
C1
B1
E
F
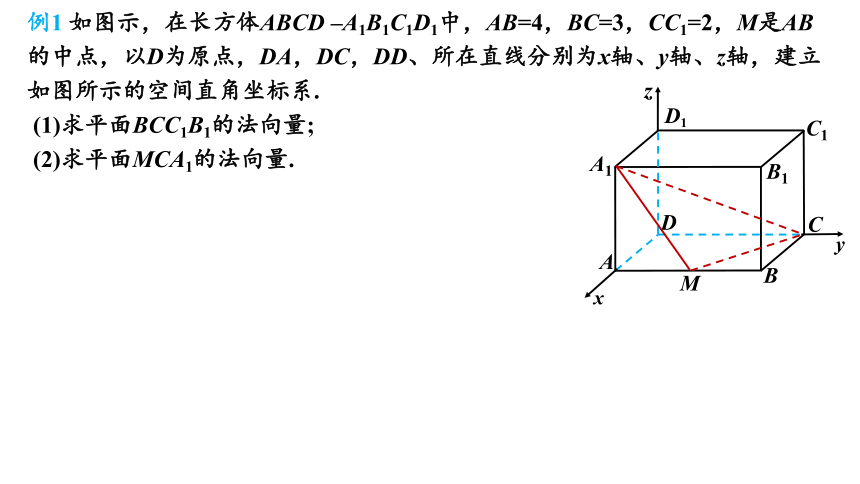
例1 如图示,在长方体ABCD –A1B1C1D1中,AB=4,BC=3,CC1=2,M是AB的中点,以D为原点,DA,DC,DD、所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系.
(1)求平面BCC1B1的法向量;
(2)求平面MCA1的法向量.
A
C
D
B
C1
D1
B1
A1
M
1. 判断下列命题是否正确,正确的在括号内打“√”,错误的打“×”.
(1) 零向量不能作为直线的方向向量和平面的法向量; ( )
(2) 若 是直线l的方向向量,则 (λ∈R)也是直线l的方向向量; ( )
(3) 在空间直角坐标系中, 是坐标平面Oxy的一个法向量. ( )
2. 在平行六面体ABCD –A1B1C1D1中, O是BD1与B1D的交点.以 为空间的一个基底,求直线OA的一个方向向量.
A
C
D
B
C1
D1
B1
A1
N
O
- - - - - - - - - - - -
练习
√
×
√
3. 在长方体ABCD –A1B1C1D1中, AB=4, BC=3, CC1=2. 以D为原点, 以
为空间的一个单位正交基底,建立空间直角坐标系Oxyz,求平面ACD1的一个法向量.
A
C
D
B
C1
D1
B1
A1
- - - - - - - - - - - -
练习
3. 在长方体ABCD –A1B1C1D1中, AB=4, BC=3, CC1=2. 以D为原点, 以
为空间的一个单位正交基底,建立空间直角坐标系Oxyz,求平面ACD1的一个法向量.
A
C
D
B
C1
D1
B1
A1
- - - - - - - - - - - -
练面法向量的方法:
(3) 根据法向量的定义建立关于x, y, z的方程组
(4) 解方程组,取其中的一个解,即得法向量.
(2) 设平面的法向量为
(1) 写出平面内的两个不共线的向量的坐标
方法一:(方程组法)
求平面法向量的方法:
(3) 根据向量叉乘计算法则可得
(4) 写出法向量坐标为
(2) 设平面的法向量为
(1) 写出平面内的两个不共线的向量的坐标
方法二:(叉乘法)
巩固训练 如图, 在四棱锥P-ABCD中, 底面ABCD是正方形, PD⊥底面ABCD, PD=DC=1, E是PC的中点, 求平面EDB的一个法向量.
A
B
C
D
P
E
x
y
z
设平面EDB的法向量为
所以平面EDB的一个法向量为
巩固训练 如图, 在四棱锥P-ABCD中, 底面ABCD是正方形, PD⊥底面ABCD, PD=DC=1, E是PC的中点, 求平面EDB的一个法向量.
A
B
C
D
P
E
x
y
z
所以平面EDB的一个法向量为
巩固训练 如图, 在四棱锥P-ABCD中, 底面ABCD是正方形, PD⊥底面ABCD, PD=DC=1, E是PC的中点, 求平面EDB的一个法向量.
A
B
C
D
P
E
x
y
z
所以平面EDB的一个法向量为
我们知道,直线的方向向量和平面的法向量是确定空间中的直线和平面的关键量,那么是否能用这些向量来刻画空间直线、平面的平行、垂直关系呢 首先来看平行的问题.
2. 空间中直线、平面的平行
思考 由直线与直线、直线与平面或平面与平面的平行关系,可以得到直线的方向向量、平面的法向量间的什么关系
如图(1)所示,设 分别是直线l1, l2的方向向量,由方向向量的定义可知,如果两条直线平行,那么它们的方向向量一定平行,反过来,如果两条直线的方向向量平行,那么这两条直线也平行,所以
(1) 直线与直线平行
l1
l2
(1)
(2) 直线与平面平行
如图(2)所示,设 是直线l的方向向量, 是平面α的法向量, 则
(3) 平面与平面平行
如图(3)所示,设 分别是平面α, β的法向量,则
α
l
(2)
m
α
(3)
β
P
m
n
例2 证明“平面与平面平行的判定定理”: 若一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
α
β
P
b
a
例3 如图示,在长方体ABCD –A1B1C1D1中,AB=4,BC=3,CC1=2. 线段B1C上是否存在点P,使得AP//平面ACD1
A
C
D
B
C1
D1
B1
A1
P
1. 用向量方法证明“直线与平面平行的判定定理”: 若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
- - - - - - - - - - - -
练习
α
b
a
2. 如图,在四面体ABCD中,E是BC的中点,直线AD上是否存在点F,使得AE//CF
A
C
D
B
E
F
- - - - - - - - - - - -
练习
3. 如图,在正方体ABCD –A1B1C1D1中,E, F分别是面AB1,面A1C1的中心.
求证: EF//平面ACD1.
A
D
C
B
A1
D1
C1
B1
F
E
- - - - - - - - - - - -
练习
∴ EF//平面ACD1.
3. 如图,在正方体ABCD –A1B1C1D1中,E, F分别是面AB1,面A1C1的中心.
求证: EF//平面ACD1.
A
D
C
B
A1
D1
C1
B1
F
E
- - - - - - - - - - - -
练习
∴ EF//平面ACD1.
x
y
z
【巩固训练1】如图所示,在正方体ABCD-A1B1C1D1中, M, N分别为D1C1, B1B的中点, 求证: DM//SN.
证法1(几何法):
A
D
D1
A1
B1
C1
B
C
F
E
N
M
又
∴
∵M, N, E, F分别为棱A1B1, A1D1, B1C1, C1D1的中点. 连接NE, 则
NE//A1 B1 ,
AB//A1 B1 ,
NE=A1B1 ,
AB=A1B1 ,
NE//AB ,
NE=AB ,
∴ ABEN为平行四边形.
∴ AN//BE.
又
AN
平面EFDB,
BE
平面EFDB,
∴ AN//平面EFDB.
同理 AM//平面EFDB.
又 AM∩AN=A,
∴ 面AMN∥面EFDB.
【巩固训练2】如图,正方体ABCD-A1B1C1D1中, M,N,E,F分别为棱A1B1, A1D1, B1C1, C1D1的中点. 求证:面AMN∥面EFDB.
A
D
D1
A1
B1
C1
B
C
F
E
N
M
证法2(向量法):
x
y
z
【巩固训练2】如图,正方体ABCD-A1B1C1D1中, M,N,E,F分别为棱A1B1, A1D1, B1C1, C1D1的中点. 求证:平面AMN∥平面EFDB.
3. 空间中直线、平面的垂直
思考 类似空间中直线、平面平行的向量表示,在直线与直线、直线与平面、平面与平面的垂直关系中,直线的方向向量、平面的法向量之间有什么关系
一般地,直线与直线垂直,就是两直线的方向向量垂直;直线与平面垂直,就是直线的方向向量与平面的法向量平行;平面与平面垂直,就是两平面的法向量垂直.
(1) 直线与直线垂直
如图(1)所示,设直线l1, l2的方向向量分别为 则
α
(1)
l1
l2
(2) 直线与平面垂直
如图(2)所示, 设直线l的方向向量为 ,平面α的法向量为 ,则
α
(2)
A
l
B
C
(3) 平面与平面垂直
如图(3)所示, 设平面α, β的法向量分别为 则
α
(3)
m
β
例4 如图示,在平行六面体ABCD-A1B1C1D1中,∠A1AB=∠A1AD=∠BAD=60°,AB=AD=AA1=1,求证: 直线A1C⊥平面BDD1B1.
A
C
D
B
C1
D1
B1
A1
例5 证明“平面与平面垂直的判定定理”: 若一个平面过另一个平面的垂线,则这两个平面垂直.
已知: 如图示, 求证: α⊥β.
α
l
β
1. 已知 是直线l的方向向量, 是平面α的法向量.
(1) 若l // α,求a, b的关系式; (2) 若l⊥α, 求a, b的值.
- - - - - - - - - - - -
练习
2.已知正方体ABCD-A1B1C1D1的棱长为1,以D为原点, 为单位正交基底建立空间直角坐标系,求证: A1C⊥BC1.
- - - - - - - - - - - -
练习
A
D
D1
A1
B1
C1
B
C
x
y
z
3.如图,在长方体ABCD-A1B1C1D1中,AB=2,BC=CC1=1,E是CD的中点,F是BC的中点,求证:平面EAD1⊥平面EFD1.
- - - - - - - - - - - -
练习
A
C
D
B
C1
D1
B1
A1
F
E
∴ 平面EAD1⊥平面EFD1.
B
C
D
A
P
E
x
y
z
【巩固训练1】如图所示, 在四棱锥P- ABCD中, PA⊥底面ABCD, 垂足为A, AB⊥AD于A, AC⊥CD于C, ∠ABC=60°, PA= AB= BC, E是PC的中点.
求证: (1) AE⊥CD; (2) PD⊥平面ABE.
证明:
【巩固训练1】如图所示, 在四棱锥P- ABCD中, PA⊥底面ABCD, 垂足为A, AB⊥AD于A, AC⊥CD于C, ∠ABC=60°, PA= AB= BC, E是PC的中点.
求证: (1) AE⊥CD; (2) PD⊥平面ABE.
B
C
D
A
P
E
x
y
z
【巩固训练1】如图所示, 在四棱锥P- ABCD中, PA⊥底面ABCD, 垂足为A, AB⊥AD于A, AC⊥CD于C, ∠ABC=60°, PA= AB= BC, E是PC的中点.
求证: (1) AE⊥CD; (2) PD⊥平面ABE.
B
C
D
A
P
E
x
y
z
A1
D1
B1
D
B
C
C1
E
F
A
x
y
z
【巩固训练2】如图所示,正方体ABCD-A1B1C1D中,E、F分别是BB1, CD的中点,求证: D1F⊥平面ADE.
x
y
z
A1
D1
B1
D
B
C
C1
A
【巩固训练3】如图,正方体ABCD-A1B1C1D. 求证: DB⊥平面ACD.
【巩固训练4】如图所示,正方体ABCD-A1B1C1D中,E是AA1的中点.
求证:平面EBD⊥平面C1BD.
B
A
A1
B1
C1
D1
C
D
E
x
y
z
课后作业:
智学网电子作业
1.4 空间向量的应用
1.4.1 用空间向量研究直线、平面的位置关系
我们已经把向量从平面推广到空间,并利用空间向量解决了一些有关空间位置关系和度量的问题。我们发现,建立空间向量与几何要素的对应关系是利用空间向量解决立体几何问题的关键.本节我们进一步运用空间向量研究立体几何中有关直线、平面的位置关系和度量问题.
立体几何问题
平面向量
推广
空间向量
研究的基本对象是点、直线、平面以及由它们组成的空间图形
研究
l
A
P
1.直线的方向向量
直线l的向量式方程:
换句话说,直线上的非零向量叫做直线的方向向量.
一、方向向量与法向量
O
我们知道,点、直线和平面是空间的基本图形,点、线段和平面图形等是组成空间几何体的基本元素,因此,为了用空间向量解决立体几何问题,首先要用向量表示空间中的点、直线和平面.
1. 空间中点、直线和平面的向量表示
思考1 如何用向量表示空间中的一个点
P
如图示,在空间中,我们取一定点O作为基点,那么空间中任意一点P就可以用向量 来表示,我们把向量 称为点P的位置向量.
直线的方向向量:
换句话说,直线上的非零向量叫做直线的方向向量.
l
A
如图,l为经过已知点A且平行于非零向量 的直线,那么非零向量 叫做直线l的方向向量.
用向量表示直线l,就是要利用点A和直线l的方向向量表示直线上的任意一点.
思考2 我们知道,空间中给定一个点A和一个方向就能唯一确定一条直线l. 如何用向量表示直线l
A
P
l
B
如图示, 是直线l的方向向量,在直线l上取 设P是直线l上的任意一点,由向量共线的条件可知,点P在直线l上的充要条件是存在实数t,使得
进一步地,如图示,取定空间中的任意一点O,可以得到点P在直线l上的充要条件是存在实数t,使
O
将 带入①式,得
①式和②式都称为空间直线的向量表示式. 由此可知,空间任意直线由直线上一点及直线的方向向量唯一确定.
思考3 一个定点和两个定方向能否确定一个平面 进一步地,一个定点和一个定方向能否确定一个平面 如果能确定,如何用向量表示这个平面
我们知道,平面α可以由α内两条相交直线确定. 如图示,设两条直线相交于点O,它们的方向向量分别为 和 ,P为平面α内任意一点,由平面向量基本定理可知,存在唯一 的有序实数对(x, y),使得
这样,点O与向量 不仅可以确定平面α,还可以具体表示出α内的任意一点. 这种表示在解决几何问题时有重要作用.
α
O
P
进一步地, 如右图示, 取定空间任意一点O, 可以得到, 空间一点P位于平面ABC内的充要条件是存在实数x, y, 使
我们把③式称为空间平面ABC的向量表示式. 由此可知,空间中任意平面由空间一点及两个不共线向量唯一确定.
α
A
P
C
B
O
2. 平面的法向量
我们知道,给定空间一点A和一条直线l,则过点A且垂直于直线l的平面是唯一确定的. 由此得到启发,我们可以利用点A和直线l的方向向量来确定平面.
如图示. 直线l⊥α. 取直线l的方向向量 , 我们称向量 为平面α的法向量. 给定一个点A和一个向量 , 那么过点A, 且以向量 为法向量的平面完全确定, 可以表示为集合
α
A
l
思考 如果另有一条直线m⊥α,在直线m上任取向量 , 与 有什么关系
m
一个平面的法向量不唯一,与平面垂直的非零向量叫做平面的法向量.
P
平面α的向量式方程:
练习 如图所示, 正方体OABCD –D1A1B1C1的棱长为1.
(1) 直线OA的一个方向向量坐标为_________;
(2) 平面OABC 的一个法向量坐标为_________;
(3) 平面AB1C 的一个法向量坐标为__________.
(-1,-1,1)
(0,0,1)
(1,0,0)
A
O
C
B
A1
D1
C1
B1
E
F
例1 如图示,在长方体ABCD –A1B1C1D1中,AB=4,BC=3,CC1=2,M是AB的中点,以D为原点,DA,DC,DD、所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系.
(1)求平面BCC1B1的法向量;
(2)求平面MCA1的法向量.
A
C
D
B
C1
D1
B1
A1
M
1. 判断下列命题是否正确,正确的在括号内打“√”,错误的打“×”.
(1) 零向量不能作为直线的方向向量和平面的法向量; ( )
(2) 若 是直线l的方向向量,则 (λ∈R)也是直线l的方向向量; ( )
(3) 在空间直角坐标系中, 是坐标平面Oxy的一个法向量. ( )
2. 在平行六面体ABCD –A1B1C1D1中, O是BD1与B1D的交点.以 为空间的一个基底,求直线OA的一个方向向量.
A
C
D
B
C1
D1
B1
A1
N
O
- - - - - - - - - - - -
练习
√
×
√
3. 在长方体ABCD –A1B1C1D1中, AB=4, BC=3, CC1=2. 以D为原点, 以
为空间的一个单位正交基底,建立空间直角坐标系Oxyz,求平面ACD1的一个法向量.
A
C
D
B
C1
D1
B1
A1
- - - - - - - - - - - -
练习
3. 在长方体ABCD –A1B1C1D1中, AB=4, BC=3, CC1=2. 以D为原点, 以
为空间的一个单位正交基底,建立空间直角坐标系Oxyz,求平面ACD1的一个法向量.
A
C
D
B
C1
D1
B1
A1
- - - - - - - - - - - -
练面法向量的方法:
(3) 根据法向量的定义建立关于x, y, z的方程组
(4) 解方程组,取其中的一个解,即得法向量.
(2) 设平面的法向量为
(1) 写出平面内的两个不共线的向量的坐标
方法一:(方程组法)
求平面法向量的方法:
(3) 根据向量叉乘计算法则可得
(4) 写出法向量坐标为
(2) 设平面的法向量为
(1) 写出平面内的两个不共线的向量的坐标
方法二:(叉乘法)
巩固训练 如图, 在四棱锥P-ABCD中, 底面ABCD是正方形, PD⊥底面ABCD, PD=DC=1, E是PC的中点, 求平面EDB的一个法向量.
A
B
C
D
P
E
x
y
z
设平面EDB的法向量为
所以平面EDB的一个法向量为
巩固训练 如图, 在四棱锥P-ABCD中, 底面ABCD是正方形, PD⊥底面ABCD, PD=DC=1, E是PC的中点, 求平面EDB的一个法向量.
A
B
C
D
P
E
x
y
z
所以平面EDB的一个法向量为
巩固训练 如图, 在四棱锥P-ABCD中, 底面ABCD是正方形, PD⊥底面ABCD, PD=DC=1, E是PC的中点, 求平面EDB的一个法向量.
A
B
C
D
P
E
x
y
z
所以平面EDB的一个法向量为
我们知道,直线的方向向量和平面的法向量是确定空间中的直线和平面的关键量,那么是否能用这些向量来刻画空间直线、平面的平行、垂直关系呢 首先来看平行的问题.
2. 空间中直线、平面的平行
思考 由直线与直线、直线与平面或平面与平面的平行关系,可以得到直线的方向向量、平面的法向量间的什么关系
如图(1)所示,设 分别是直线l1, l2的方向向量,由方向向量的定义可知,如果两条直线平行,那么它们的方向向量一定平行,反过来,如果两条直线的方向向量平行,那么这两条直线也平行,所以
(1) 直线与直线平行
l1
l2
(1)
(2) 直线与平面平行
如图(2)所示,设 是直线l的方向向量, 是平面α的法向量, 则
(3) 平面与平面平行
如图(3)所示,设 分别是平面α, β的法向量,则
α
l
(2)
m
α
(3)
β
P
m
n
例2 证明“平面与平面平行的判定定理”: 若一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
α
β
P
b
a
例3 如图示,在长方体ABCD –A1B1C1D1中,AB=4,BC=3,CC1=2. 线段B1C上是否存在点P,使得AP//平面ACD1
A
C
D
B
C1
D1
B1
A1
P
1. 用向量方法证明“直线与平面平行的判定定理”: 若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
- - - - - - - - - - - -
练习
α
b
a
2. 如图,在四面体ABCD中,E是BC的中点,直线AD上是否存在点F,使得AE//CF
A
C
D
B
E
F
- - - - - - - - - - - -
练习
3. 如图,在正方体ABCD –A1B1C1D1中,E, F分别是面AB1,面A1C1的中心.
求证: EF//平面ACD1.
A
D
C
B
A1
D1
C1
B1
F
E
- - - - - - - - - - - -
练习
∴ EF//平面ACD1.
3. 如图,在正方体ABCD –A1B1C1D1中,E, F分别是面AB1,面A1C1的中心.
求证: EF//平面ACD1.
A
D
C
B
A1
D1
C1
B1
F
E
- - - - - - - - - - - -
练习
∴ EF//平面ACD1.
x
y
z
【巩固训练1】如图所示,在正方体ABCD-A1B1C1D1中, M, N分别为D1C1, B1B的中点, 求证: DM//SN.
证法1(几何法):
A
D
D1
A1
B1
C1
B
C
F
E
N
M
又
∴
∵M, N, E, F分别为棱A1B1, A1D1, B1C1, C1D1的中点. 连接NE, 则
NE//A1 B1 ,
AB//A1 B1 ,
NE=A1B1 ,
AB=A1B1 ,
NE//AB ,
NE=AB ,
∴ ABEN为平行四边形.
∴ AN//BE.
又
AN
平面EFDB,
BE
平面EFDB,
∴ AN//平面EFDB.
同理 AM//平面EFDB.
又 AM∩AN=A,
∴ 面AMN∥面EFDB.
【巩固训练2】如图,正方体ABCD-A1B1C1D1中, M,N,E,F分别为棱A1B1, A1D1, B1C1, C1D1的中点. 求证:面AMN∥面EFDB.
A
D
D1
A1
B1
C1
B
C
F
E
N
M
证法2(向量法):
x
y
z
【巩固训练2】如图,正方体ABCD-A1B1C1D1中, M,N,E,F分别为棱A1B1, A1D1, B1C1, C1D1的中点. 求证:平面AMN∥平面EFDB.
3. 空间中直线、平面的垂直
思考 类似空间中直线、平面平行的向量表示,在直线与直线、直线与平面、平面与平面的垂直关系中,直线的方向向量、平面的法向量之间有什么关系
一般地,直线与直线垂直,就是两直线的方向向量垂直;直线与平面垂直,就是直线的方向向量与平面的法向量平行;平面与平面垂直,就是两平面的法向量垂直.
(1) 直线与直线垂直
如图(1)所示,设直线l1, l2的方向向量分别为 则
α
(1)
l1
l2
(2) 直线与平面垂直
如图(2)所示, 设直线l的方向向量为 ,平面α的法向量为 ,则
α
(2)
A
l
B
C
(3) 平面与平面垂直
如图(3)所示, 设平面α, β的法向量分别为 则
α
(3)
m
β
例4 如图示,在平行六面体ABCD-A1B1C1D1中,∠A1AB=∠A1AD=∠BAD=60°,AB=AD=AA1=1,求证: 直线A1C⊥平面BDD1B1.
A
C
D
B
C1
D1
B1
A1
例5 证明“平面与平面垂直的判定定理”: 若一个平面过另一个平面的垂线,则这两个平面垂直.
已知: 如图示, 求证: α⊥β.
α
l
β
1. 已知 是直线l的方向向量, 是平面α的法向量.
(1) 若l // α,求a, b的关系式; (2) 若l⊥α, 求a, b的值.
- - - - - - - - - - - -
练习
2.已知正方体ABCD-A1B1C1D1的棱长为1,以D为原点, 为单位正交基底建立空间直角坐标系,求证: A1C⊥BC1.
- - - - - - - - - - - -
练习
A
D
D1
A1
B1
C1
B
C
x
y
z
3.如图,在长方体ABCD-A1B1C1D1中,AB=2,BC=CC1=1,E是CD的中点,F是BC的中点,求证:平面EAD1⊥平面EFD1.
- - - - - - - - - - - -
练习
A
C
D
B
C1
D1
B1
A1
F
E
∴ 平面EAD1⊥平面EFD1.
B
C
D
A
P
E
x
y
z
【巩固训练1】如图所示, 在四棱锥P- ABCD中, PA⊥底面ABCD, 垂足为A, AB⊥AD于A, AC⊥CD于C, ∠ABC=60°, PA= AB= BC, E是PC的中点.
求证: (1) AE⊥CD; (2) PD⊥平面ABE.
证明:
【巩固训练1】如图所示, 在四棱锥P- ABCD中, PA⊥底面ABCD, 垂足为A, AB⊥AD于A, AC⊥CD于C, ∠ABC=60°, PA= AB= BC, E是PC的中点.
求证: (1) AE⊥CD; (2) PD⊥平面ABE.
B
C
D
A
P
E
x
y
z
【巩固训练1】如图所示, 在四棱锥P- ABCD中, PA⊥底面ABCD, 垂足为A, AB⊥AD于A, AC⊥CD于C, ∠ABC=60°, PA= AB= BC, E是PC的中点.
求证: (1) AE⊥CD; (2) PD⊥平面ABE.
B
C
D
A
P
E
x
y
z
A1
D1
B1
D
B
C
C1
E
F
A
x
y
z
【巩固训练2】如图所示,正方体ABCD-A1B1C1D中,E、F分别是BB1, CD的中点,求证: D1F⊥平面ADE.
x
y
z
A1
D1
B1
D
B
C
C1
A
【巩固训练3】如图,正方体ABCD-A1B1C1D. 求证: DB⊥平面ACD.
【巩固训练4】如图所示,正方体ABCD-A1B1C1D中,E是AA1的中点.
求证:平面EBD⊥平面C1BD.
B
A
A1
B1
C1
D1
C
D
E
x
y
z
课后作业:
智学网电子作业
