2021-2022学年高一上学期数学人教A版(2019)必修第一册5.5.2简单的三角恒等变换 课件(共18张PPT)
文档属性
| 名称 | 2021-2022学年高一上学期数学人教A版(2019)必修第一册5.5.2简单的三角恒等变换 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
5.5.2 简单的三角恒等变换
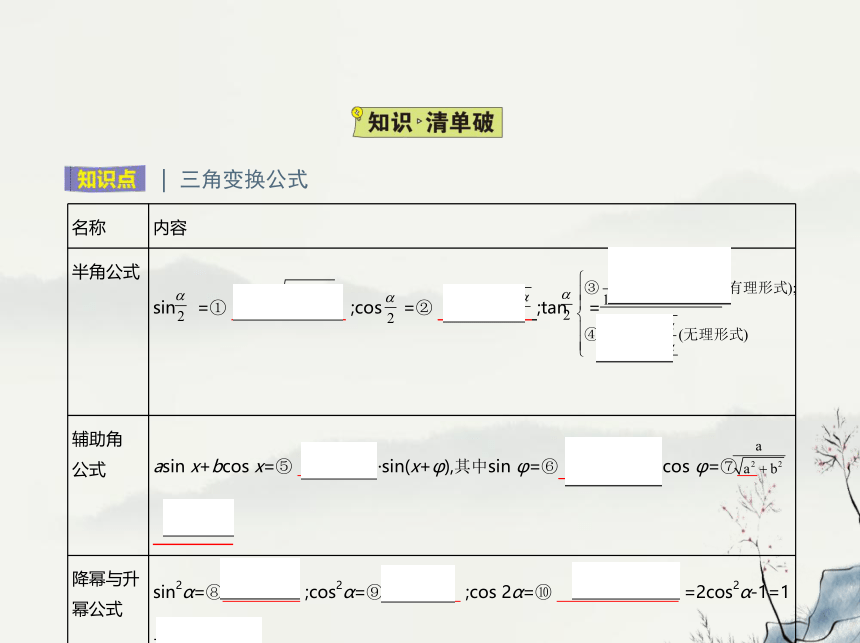
| 三角变换公式
名称 内容
半角公式 sin =① ± ;cos =② ± ;tan =
辅助角 公式 asin x+bcos x=⑤ ·sin(x+φ),其中sin φ=⑥ ,cos φ=⑦
降幂与升幂公式 sin2α=⑧ ;cos2α=⑨ ;cos 2α=⑩ cos2α-sin2α =2cos2α-1=1-2sin2α;
tan 2α=
名称 内容
积化和差公式 (1)sin α·cos β= [sin(α+β)+sin(α-β)];(2)cos α·sin β= [sin(α+β)-sin(α-β)];
(3)cos α·cos β= [cos(α+β)+cos(α-β)];(4)sin α·sin β=- [cos(α+β)-cos(α-β)]
和差化积公式 (1)sin θ+sin φ=2sin cos ;(2)sin θ-sin φ=2cos sin ;
(3)cos θ+cos φ=2cos cos ;(4)cos θ-cos φ=-2sin sin
续表
1.cos = . ( )
提示:只有当- +2kπ≤ ≤ +2kπ(k∈Z),即-π+4kπ≤α≤π+4kπ(k∈Z)时,cos =
.
2.对于任意α∈R,sin = sin α都不成立.( )
提示:当α=2kπ(k∈Z)时,等式成立,但一般情况下不成立.
3.对任意α∈R都有sin α+ cos α=2sin . ( √ )
4.若5π<θ<6π,cos =a,则cos = . ( )
提示:∵5π<θ<6π,∴ ∈ ,即 为第三象限角,∴cos =- .
判断正误,正确的画“ √” ,错误的画“ ” .
1 | 半角公式的运用
利用半角公式求值的思路
(1)看角:看已知角与待求角的二倍关系.
(2)明范围:求出相应半角的范围为定符号做准备.
(3)选公式:涉及半角公式的正切值时,常利用tan = = 计算,涉及半
角公式的正、余弦值时,常利用sin2 = ,cos2 = 计算.
(4)下结论:结合(2)求值.
已知θ∈ 且sin θ= ,求sin ,cos ,tan 的值.
解析 解法一:∵θ∈ ,且sin θ= ,
∴cos θ=- , ∈ ,
∴sin =- =- ,
cos =- =- , 从而tan = =2.
解法二:sin 与cos 的求法同解法一.
tan = = =2.
2 | 三角恒等式的证明与三角函数式的化简
1.三角恒等式证明的常用方法
(1)由因导果法:证明的方式一般是化繁为简;
(2)左右归一法:证明等号两边都等于同一个式子;
(3)拼凑法:针对题设和结论之间的差异,有针对性地变形,以消除它们之间的差异,
即化异求同;
(4)比较法:设法证明“左边-右边=0”或“ =1(右边≠0)”;
(5)分析法:即执果索因法,从被证明的等式出发,逐步地探求使等式成立的条件,直
到符合已知条件或出现明显的事实为止,就可以断定原等式成立.
2.化简三角函数式的基本思路
三角函数式的化简是三角恒等变换的一个重要方面,其基本方法是统一角,统一
三角函数的名称.常用方法:异名函数化为同名函数,异角化为同角,异次化为同次,
弦切互化,特殊角的三角函数与特殊值的互化等.在具体实施过程中,应着重抓住
“角”的统一,通过观察角、函数名、项的次数等,找到突破口,利用切化弦、升
幂、降幂、逆用公式等手段将其化简.化简的结果应满足以下几点:①能求值尽
量求值;②函数名称尽量少;③项数尽量少;④次数尽量低;⑤分母、根号下尽量不
含三角函数.
(1)求证: + = ;
(2)在△ABC中,角A,B,C的对边分别为a,b,c,已知cos A= ,求证: =
.
思路点拨
(1)等式的左边较复杂,将左边化简得到右边,可以先化简分式再通分,也可以先通
分再化简.
(2)易得tan2 = ,tan2 = ,所以所证结论等价于: =
,由条件分别计算1-cos A,1+cos A即可得到结论.
证明 (1)证法一:左边= + = + =
= =右边.
所以原等式成立.
证法二:左边=
= = = =右边.
所以原等式成立.
(2)因为cos A= ,
所以1-cos A= ,
1+cos A= ,
因此 = ,
而 = =tan2 ,
= =tan2 ,
所以tan2 = ·tan2 ,即 = .
化简: .
思路点拨
从角的角度考虑到 +x与 -x互余,从函数名称的角度考虑到切化弦,从运算的角
度考虑到降次、消项和逆用公式,综合考虑这些因素逐步运用公式,达到化简的
目的.
解析 原式=
=
= = cos 2x.
如图,制图工程师要用两个同中心的边长均为4的正方形合成一个八角形图
形,由对称性知,图中8个三角形是全等三角形,设∠AA1H1=α.
3| 辅助角公式的运用
问题
1.你能用α表示线段A1H1吗
提示:由题意可得AA1+A1H1+AH1=A1H1cos α+A1H1+A1H1sin α=4,所以A1H1=
,α∈ .
2.如何求A1H1的最值
提示:先利用辅助角公式把分母化为一个角的同一三角函数,再求解.
1.(1)公式形式:asin α+bcos α= sin(α+φ)
或asin α+bcos α= ·cos(α-φ) 其中sin φ= ,cos φ= .
(2)形式选择:化为正弦还是余弦,要看具体条件而定,一般要求变形后角α的系数
为正,这样更有利于研究函数的性质.
2.应用辅助角公式可将不同名的三角函数式的和(差)转化为一个三角函数式,从
而可结合三角函数的有关知识解决问题.在实际解题时,要注意灵活掌握该
公式,合理引入辅助角,确定各量之间的关系,实现“合二为一”.
已知函数f(x)=sin2x-sin2 ,x∈R.
(1)求f(x)的最小正周期;
(2)求f(x)在区间 上的最大值和最小值.
思路点拨
先利用三角恒等变换将函数f(x)化为f(x)=Asin(ωx+φ)+B的形式,再根据三角函数
的性质求解.
解析 (1)由已知,得f(x)= - = - cos 2x=
sin 2x- cos 2x= sin .
所以f(x)的最小正周期T= =π.
(2)因为x∈ ,
所以2x- ∈ ,
所以sin ∈ , f(x)∈ ,
所以f(x)在区间 上的最大值为 ,最小值为- .
5.5.2 简单的三角恒等变换
| 三角变换公式
名称 内容
半角公式 sin =① ± ;cos =② ± ;tan =
辅助角 公式 asin x+bcos x=⑤ ·sin(x+φ),其中sin φ=⑥ ,cos φ=⑦
降幂与升幂公式 sin2α=⑧ ;cos2α=⑨ ;cos 2α=⑩ cos2α-sin2α =2cos2α-1=1-2sin2α;
tan 2α=
名称 内容
积化和差公式 (1)sin α·cos β= [sin(α+β)+sin(α-β)];(2)cos α·sin β= [sin(α+β)-sin(α-β)];
(3)cos α·cos β= [cos(α+β)+cos(α-β)];(4)sin α·sin β=- [cos(α+β)-cos(α-β)]
和差化积公式 (1)sin θ+sin φ=2sin cos ;(2)sin θ-sin φ=2cos sin ;
(3)cos θ+cos φ=2cos cos ;(4)cos θ-cos φ=-2sin sin
续表
1.cos = . ( )
提示:只有当- +2kπ≤ ≤ +2kπ(k∈Z),即-π+4kπ≤α≤π+4kπ(k∈Z)时,cos =
.
2.对于任意α∈R,sin = sin α都不成立.( )
提示:当α=2kπ(k∈Z)时,等式成立,但一般情况下不成立.
3.对任意α∈R都有sin α+ cos α=2sin . ( √ )
4.若5π<θ<6π,cos =a,则cos = . ( )
提示:∵5π<θ<6π,∴ ∈ ,即 为第三象限角,∴cos =- .
判断正误,正确的画“ √” ,错误的画“ ” .
1 | 半角公式的运用
利用半角公式求值的思路
(1)看角:看已知角与待求角的二倍关系.
(2)明范围:求出相应半角的范围为定符号做准备.
(3)选公式:涉及半角公式的正切值时,常利用tan = = 计算,涉及半
角公式的正、余弦值时,常利用sin2 = ,cos2 = 计算.
(4)下结论:结合(2)求值.
已知θ∈ 且sin θ= ,求sin ,cos ,tan 的值.
解析 解法一:∵θ∈ ,且sin θ= ,
∴cos θ=- , ∈ ,
∴sin =- =- ,
cos =- =- , 从而tan = =2.
解法二:sin 与cos 的求法同解法一.
tan = = =2.
2 | 三角恒等式的证明与三角函数式的化简
1.三角恒等式证明的常用方法
(1)由因导果法:证明的方式一般是化繁为简;
(2)左右归一法:证明等号两边都等于同一个式子;
(3)拼凑法:针对题设和结论之间的差异,有针对性地变形,以消除它们之间的差异,
即化异求同;
(4)比较法:设法证明“左边-右边=0”或“ =1(右边≠0)”;
(5)分析法:即执果索因法,从被证明的等式出发,逐步地探求使等式成立的条件,直
到符合已知条件或出现明显的事实为止,就可以断定原等式成立.
2.化简三角函数式的基本思路
三角函数式的化简是三角恒等变换的一个重要方面,其基本方法是统一角,统一
三角函数的名称.常用方法:异名函数化为同名函数,异角化为同角,异次化为同次,
弦切互化,特殊角的三角函数与特殊值的互化等.在具体实施过程中,应着重抓住
“角”的统一,通过观察角、函数名、项的次数等,找到突破口,利用切化弦、升
幂、降幂、逆用公式等手段将其化简.化简的结果应满足以下几点:①能求值尽
量求值;②函数名称尽量少;③项数尽量少;④次数尽量低;⑤分母、根号下尽量不
含三角函数.
(1)求证: + = ;
(2)在△ABC中,角A,B,C的对边分别为a,b,c,已知cos A= ,求证: =
.
思路点拨
(1)等式的左边较复杂,将左边化简得到右边,可以先化简分式再通分,也可以先通
分再化简.
(2)易得tan2 = ,tan2 = ,所以所证结论等价于: =
,由条件分别计算1-cos A,1+cos A即可得到结论.
证明 (1)证法一:左边= + = + =
= =右边.
所以原等式成立.
证法二:左边=
= = = =右边.
所以原等式成立.
(2)因为cos A= ,
所以1-cos A= ,
1+cos A= ,
因此 = ,
而 = =tan2 ,
= =tan2 ,
所以tan2 = ·tan2 ,即 = .
化简: .
思路点拨
从角的角度考虑到 +x与 -x互余,从函数名称的角度考虑到切化弦,从运算的角
度考虑到降次、消项和逆用公式,综合考虑这些因素逐步运用公式,达到化简的
目的.
解析 原式=
=
= = cos 2x.
如图,制图工程师要用两个同中心的边长均为4的正方形合成一个八角形图
形,由对称性知,图中8个三角形是全等三角形,设∠AA1H1=α.
3| 辅助角公式的运用
问题
1.你能用α表示线段A1H1吗
提示:由题意可得AA1+A1H1+AH1=A1H1cos α+A1H1+A1H1sin α=4,所以A1H1=
,α∈ .
2.如何求A1H1的最值
提示:先利用辅助角公式把分母化为一个角的同一三角函数,再求解.
1.(1)公式形式:asin α+bcos α= sin(α+φ)
或asin α+bcos α= ·cos(α-φ) 其中sin φ= ,cos φ= .
(2)形式选择:化为正弦还是余弦,要看具体条件而定,一般要求变形后角α的系数
为正,这样更有利于研究函数的性质.
2.应用辅助角公式可将不同名的三角函数式的和(差)转化为一个三角函数式,从
而可结合三角函数的有关知识解决问题.在实际解题时,要注意灵活掌握该
公式,合理引入辅助角,确定各量之间的关系,实现“合二为一”.
已知函数f(x)=sin2x-sin2 ,x∈R.
(1)求f(x)的最小正周期;
(2)求f(x)在区间 上的最大值和最小值.
思路点拨
先利用三角恒等变换将函数f(x)化为f(x)=Asin(ωx+φ)+B的形式,再根据三角函数
的性质求解.
解析 (1)由已知,得f(x)= - = - cos 2x=
sin 2x- cos 2x= sin .
所以f(x)的最小正周期T= =π.
(2)因为x∈ ,
所以2x- ∈ ,
所以sin ∈ , f(x)∈ ,
所以f(x)在区间 上的最大值为 ,最小值为- .
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
