沪科版2021-2022学年度八年级数学上册 12.3一次函数与二元一次方程课件(共23张PPT)
文档属性
| 名称 | 沪科版2021-2022学年度八年级数学上册 12.3一次函数与二元一次方程课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
一次函数
二元一次方程
2x-y-3=0
y=2x-3
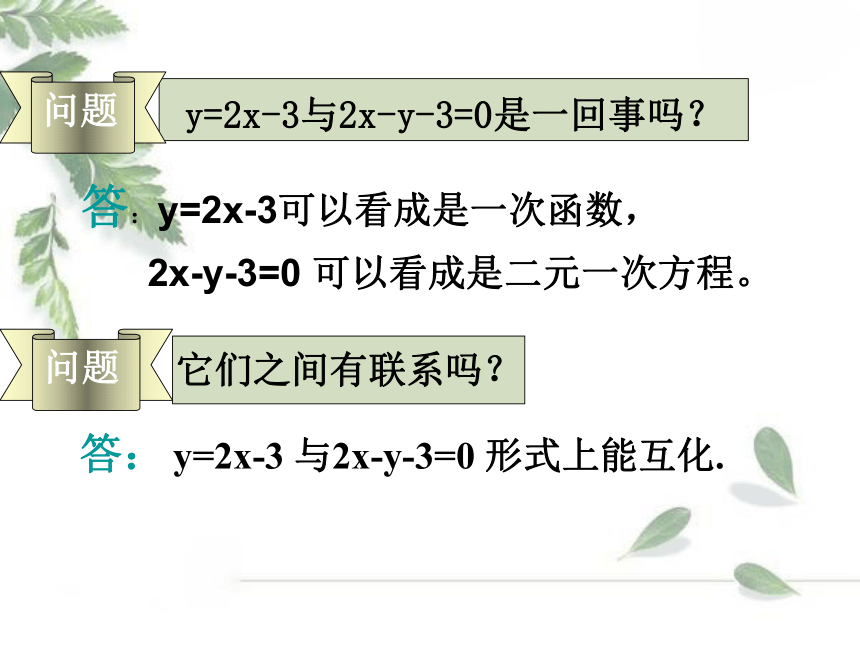
y=2x-3这是什么?
它们之间有联系吗?
y=2x-3与2x-y-3=0是一回事吗?
答:y=2x-3可以看成是一次函数,
2x-y-3=0 可以看成是二元一次方程。
问题
答: y=2x-3 与2x-y-3=0 形式上能互化.
问题
方程2x-y-3=0的解有多少个?能写出其中的几组解来吗?
(-1,-5) 、(0,-3)、(1,-1)、(3/2,0)、(2,1) ……
活动一
把这些解能写成坐标的形式吗?
这些点在y=2x-3的图象上吗?
……
(-1,-5) 、(0,-3)、(1,-1)、(3/2,0)、(2,1) ……
活动二
这些点在y=2x-3的图象上吗?
y=2x-3
问题一:在一次函数y=2x-3的图象上再取几个点,它的坐标适合方程2x-y-3=0吗?
问题二:以方程2x-y-3=0的解为坐标的所有点组成的图象与一次函数y=2x-3的图象相同吗?
(3,3)
(4,5)
(-2,-7)
结论:一次函数y=kx+b图象上任意一点的坐标都是二元一次方程kx-y+b=0的解;
结论
问题:一次函数y=kx+b图象与二元一次方程kx-y+b=0的解有何关系?
以二元一次方程 kx-y+b=0的解为坐标的点都在一次函数y=kx+b图象上。
一次函数与二元一次方程可以相互转化的,从形式到内容它们都是统一的。
二元一次方程kx-y+b=0的图象就是一次函数的y=kx+b的图象,它是一条直线。
在平面直角坐标系内画出下列二元一次方程的图象:
(1)x-y=0; (2)x+y=0;
(3)3x+y=6; (4)4x-5y+10=0.
练习
活动三
问题1:在同一直角坐标系内分别作出一次函数y=2x-3和y=x+1的图象,这两个图象有交点吗?交点坐标是多少?
问题2:
这两个问题之间有关系吗?
活动四
一次函数y=2x-3和y=x+1的图象交点坐标是(4,5)
y=2x-3
y=x+1
(4,5)
是巧合吗?
能解释吗?
结论
如果两个一次函数的图象有一个交点,那么交点的坐标就是相应的二元一次方程组的解。
问题:两个一次函数的图象的交点与相应的二元一次方程组的解有关系吗?
图象法解二元一次方程组:
先在同一平面坐标系内画出每一个二元一次方程的直线。这两条直线若相交,其交点的坐标,就是方程组的解。
归纳总结:
从函数的观点看解
二元一次方程组
从“形”的角度看:解方程组相当于确定两条
直线的 交点坐标 。
从“数”的角度看:解方程组相当于考虑
当 自变量 为何值时,两个 函数值相等
以及这个函数值是何值。
1、利用一次函数图象解二元一次方程组
练一练
(2,2)
解:由x-2y=-2得y= x+1;
由2x-y=2得y=2x-2.
在同一坐标系中作出一次函数y=+1和y=2x-2的图象。
观察图象得,两直线交于点(2,2).
所以原方程组的解为
2、求y=x+3与y=-2x+3的交点坐标。
做一做
y=-2x+3
(0,3)
y=x+3
x-y=-1,①
2x+y=1。②
1、利用图象法解方程组:
观察图象得,交点(0,-1)
所以方程组的解为
x=0
y=-1
y=-2x+4
解:由①得y=x+1;
由②得y=-2x+1.
作出图象:
y
O
x
问题:这两条直线有怎样的位置关系?有多少个交点?
答:因为两直线相交,所以方程组有一组解。
y=x+1
y
x
o
5x-2y=4
10x-4y=8
2、利用图象解方程组
(2)画图.
y=5/2x-2
y=10/4x-2
问题:这两条直线有怎样的位置关系?有多少个交点?
答:因为两直线重合,所以方程组有无数组解。
x+y=-2
2x+2y=5
3、利用图象解方程组
(1)转化
y= -x-2
y= -x+2.5
y
x
0
(2)画图.
y= -x-2
y= -x+2.5
问题:两条直线有什么位置关系 方程组解的情况怎样
答:两直线平行,无交点,故方程组无解。
通过以上各例及练习,你能说说二元一次
方程组的解的情况吗?有什么样的规律吗?
二元一次方程组
a1x+b1y=c1,
a2x+b2y=c2
的解的情况有三种:
当 a1:a2 ≠b1:b2 时 ,方程组有唯一解;
当 a1:a2=b1:b2 =c1 :c2时,方程组有无穷多解;
当a1:a2=b1:b2 ≠c1 :c2时,方程组无解。
两个一次函数的图象相交(有一个交点)
两个一次函数的图象平行(无交点)
两个一次函数的图象重合(有无数个交点)
归一归
二元一次方程组有一解
二元一次方程组无解
二元一次方程组有无数个解
二元一次方程组与一次函数的关系:
请同学们谈本节课的收获!
小结
请同学们谈本节课的收获!
小结
学而不思则罔,思而不学则殆。
——孔子
一次函数
二元一次方程
2x-y-3=0
y=2x-3
y=2x-3这是什么?
它们之间有联系吗?
y=2x-3与2x-y-3=0是一回事吗?
答:y=2x-3可以看成是一次函数,
2x-y-3=0 可以看成是二元一次方程。
问题
答: y=2x-3 与2x-y-3=0 形式上能互化.
问题
方程2x-y-3=0的解有多少个?能写出其中的几组解来吗?
(-1,-5) 、(0,-3)、(1,-1)、(3/2,0)、(2,1) ……
活动一
把这些解能写成坐标的形式吗?
这些点在y=2x-3的图象上吗?
……
(-1,-5) 、(0,-3)、(1,-1)、(3/2,0)、(2,1) ……
活动二
这些点在y=2x-3的图象上吗?
y=2x-3
问题一:在一次函数y=2x-3的图象上再取几个点,它的坐标适合方程2x-y-3=0吗?
问题二:以方程2x-y-3=0的解为坐标的所有点组成的图象与一次函数y=2x-3的图象相同吗?
(3,3)
(4,5)
(-2,-7)
结论:一次函数y=kx+b图象上任意一点的坐标都是二元一次方程kx-y+b=0的解;
结论
问题:一次函数y=kx+b图象与二元一次方程kx-y+b=0的解有何关系?
以二元一次方程 kx-y+b=0的解为坐标的点都在一次函数y=kx+b图象上。
一次函数与二元一次方程可以相互转化的,从形式到内容它们都是统一的。
二元一次方程kx-y+b=0的图象就是一次函数的y=kx+b的图象,它是一条直线。
在平面直角坐标系内画出下列二元一次方程的图象:
(1)x-y=0; (2)x+y=0;
(3)3x+y=6; (4)4x-5y+10=0.
练习
活动三
问题1:在同一直角坐标系内分别作出一次函数y=2x-3和y=x+1的图象,这两个图象有交点吗?交点坐标是多少?
问题2:
这两个问题之间有关系吗?
活动四
一次函数y=2x-3和y=x+1的图象交点坐标是(4,5)
y=2x-3
y=x+1
(4,5)
是巧合吗?
能解释吗?
结论
如果两个一次函数的图象有一个交点,那么交点的坐标就是相应的二元一次方程组的解。
问题:两个一次函数的图象的交点与相应的二元一次方程组的解有关系吗?
图象法解二元一次方程组:
先在同一平面坐标系内画出每一个二元一次方程的直线。这两条直线若相交,其交点的坐标,就是方程组的解。
归纳总结:
从函数的观点看解
二元一次方程组
从“形”的角度看:解方程组相当于确定两条
直线的 交点坐标 。
从“数”的角度看:解方程组相当于考虑
当 自变量 为何值时,两个 函数值相等
以及这个函数值是何值。
1、利用一次函数图象解二元一次方程组
练一练
(2,2)
解:由x-2y=-2得y= x+1;
由2x-y=2得y=2x-2.
在同一坐标系中作出一次函数y=+1和y=2x-2的图象。
观察图象得,两直线交于点(2,2).
所以原方程组的解为
2、求y=x+3与y=-2x+3的交点坐标。
做一做
y=-2x+3
(0,3)
y=x+3
x-y=-1,①
2x+y=1。②
1、利用图象法解方程组:
观察图象得,交点(0,-1)
所以方程组的解为
x=0
y=-1
y=-2x+4
解:由①得y=x+1;
由②得y=-2x+1.
作出图象:
y
O
x
问题:这两条直线有怎样的位置关系?有多少个交点?
答:因为两直线相交,所以方程组有一组解。
y=x+1
y
x
o
5x-2y=4
10x-4y=8
2、利用图象解方程组
(2)画图.
y=5/2x-2
y=10/4x-2
问题:这两条直线有怎样的位置关系?有多少个交点?
答:因为两直线重合,所以方程组有无数组解。
x+y=-2
2x+2y=5
3、利用图象解方程组
(1)转化
y= -x-2
y= -x+2.5
y
x
0
(2)画图.
y= -x-2
y= -x+2.5
问题:两条直线有什么位置关系 方程组解的情况怎样
答:两直线平行,无交点,故方程组无解。
通过以上各例及练习,你能说说二元一次
方程组的解的情况吗?有什么样的规律吗?
二元一次方程组
a1x+b1y=c1,
a2x+b2y=c2
的解的情况有三种:
当 a1:a2 ≠b1:b2 时 ,方程组有唯一解;
当 a1:a2=b1:b2 =c1 :c2时,方程组有无穷多解;
当a1:a2=b1:b2 ≠c1 :c2时,方程组无解。
两个一次函数的图象相交(有一个交点)
两个一次函数的图象平行(无交点)
两个一次函数的图象重合(有无数个交点)
归一归
二元一次方程组有一解
二元一次方程组无解
二元一次方程组有无数个解
二元一次方程组与一次函数的关系:
请同学们谈本节课的收获!
小结
请同学们谈本节课的收获!
小结
学而不思则罔,思而不学则殆。
——孔子
