沪科版2021-2022学年度八年级数学上册 12.4综合与实践课件(共16张PPT)
文档属性
| 名称 | 沪科版2021-2022学年度八年级数学上册 12.4综合与实践课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 727.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 21:06:22 | ||
图片预览





文档简介
(共16张PPT)
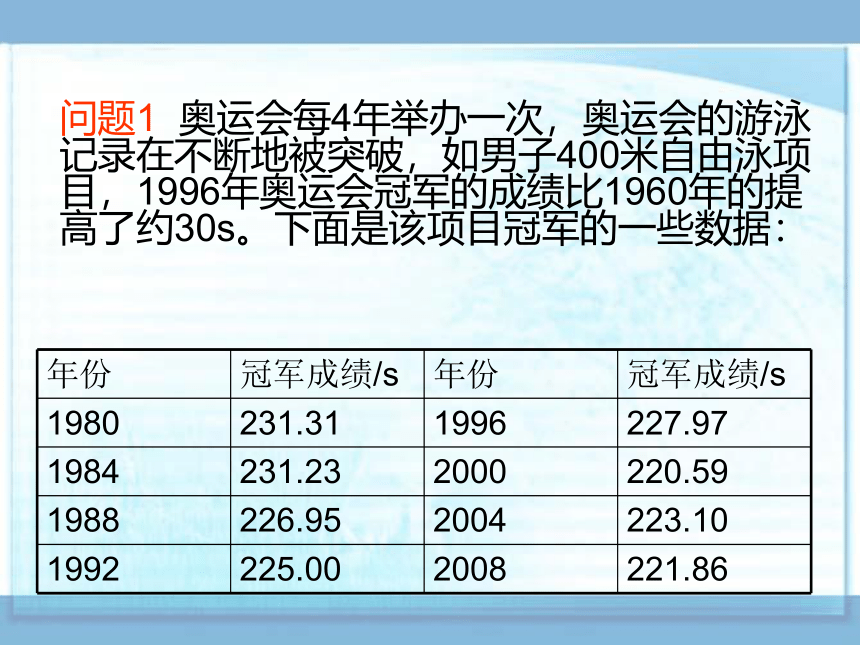
年份 冠军成绩/s 年份 冠军成绩/s
1980 231.31 1996 227.97
1984 231.23 2000 220.59
1988 226.95 2004 223.10
1992 225.00 2008 221.86
问题1 奥运会每4年举办一次,奥运会的游泳记录在不断地被突破,如男子400米自由泳项目,1996年奥运会冠军的成绩比1960年的提高了约30s。下面是该项目冠军的一些数据:
根据上面资料,你能否估计2012年伦敦奥运会时该项目的奥运会冠军成绩?
按照下面的步骤做,看能否预测出结果?
1、将数据在直角坐标系中描出。 2、观察这些点的特征,确定选用的函数形式,根据已知数据确定函数表达式。 3、检验。 4、应用此函数模型解题。
2012年伦敦奥运会中国选手孙杨以220.14s
的成绩打破男子400米自由泳项目的奥运会
纪录获得冠军,你预测的程度如何?
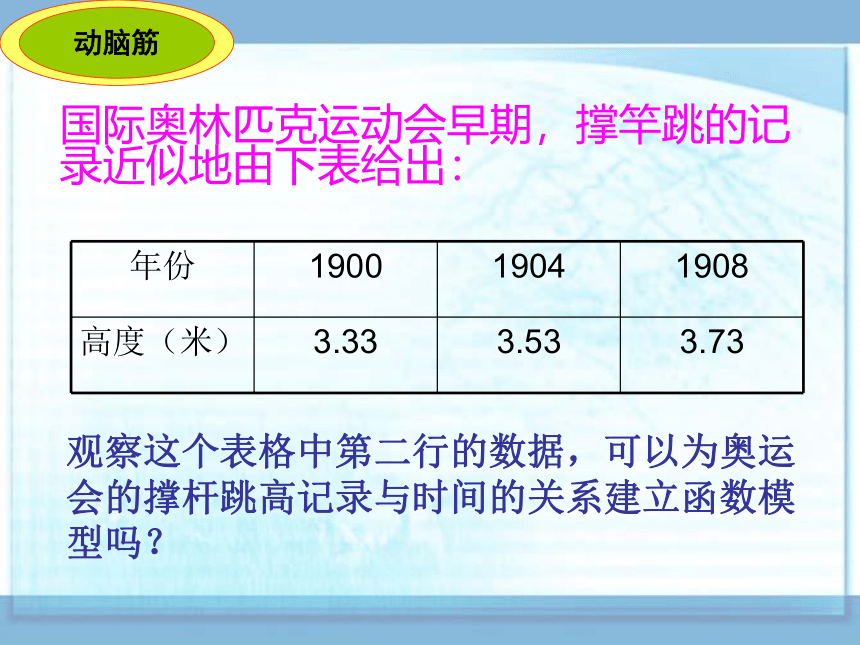
国际奥林匹克运动会早期,撑竿跳的记录近似地由下表给出:
动脑筋
年份 1900 1904 1908
高度(米) 3.33 3.53 3.73
观察这个表格中第二行的数据,可以为奥运会的撑杆跳高记录与时间的关系建立函数模型吗?
上表中每一届比上一届的记录提高了0.2米,可以试着建立一次函数的模型。
用t表示从1900年期增加的年份,则在奥与那会早期,撑杆跳高的记录y(米)与t的函数关系式为
y = kt + b
由于t=0(即1900年)时,长杆调高的记录为3.33米,t=4(即1904年)时,记录为3.53米,因此
b=3.33 ①
4k+b=3.35 ②
b=3.33 ①
4k+b=3.35 ②
把①代入②,得 4k+3.33=3.35
解得 k=0.05.
于是 y=0.05t+3.33. (D)
所以奥运会早期撑杆跳高记录y与时间t的函数关系式为:
y=0.05t+3.33.
你能利用公式(D)预测1912年奥运会的撑杆跳高记录吗?
做一做
y=0.05×12+3.33=3.93(米)
1912年奥运会撑杆跳高记录的却约为3.93米。这说明用所建立的函数模型,在已知数据邻近做预测,是与实际事实比较吻合的。
能够用公式(D)预测20世纪80年代,譬如1988年的奥运会撑杆跳高记录吗?
y=0.05×88+3.33=7.73(米)
实际上,1988年奥运会的撑杆跳高记录是6.06米,远低于7.73米。这表明用所建立的函数模型,原理已知数据作预测是不可靠的。
实验次数 第1次 第2次 第3次 第4次 第5次 第6次
下落高度/cm
反弹高度/cm
问题2 球从高处下落再反弹起来,可以直观地看出球的下落高度越高,反弹高度也就越高,那么球下落高度与反弹高度具有怎样的关系呢?请你进行实验,将实验数据填入下表,并根据实验数据建立球下落高度和反弹高度之间关系的函数模型。
1. 与同桌同学讨论,为什么用公式(D)预测1988年奥运会撑杆跳高记录高于实际记录?
练习
小明在练习100米短跑,今年1月至4月份的100米短跑成绩入校表所示:
练习
月份 1 2 3 4
成绩(秒)
1.56
1.54
1.52
15
(1)你能为小明的100米短跑成绩与时间的关系建立函数关系模型吗?
(2)用所求出的函数解析式预测小明今年6月份的100米短跑成绩。
(3)能用所求出的解析式预测小明明年12月份的100米短跑成绩吗?
同学们这节课有哪些收获?
建立函数模型的步骤: 1、将数据在直角坐标系中描出。 2、观察这些点的特征,确定选用的函数形式,根据已知数据确定函数表达式。 3、检验。 4、应用此函数模型解题。
年份 冠军成绩/s 年份 冠军成绩/s
1980 231.31 1996 227.97
1984 231.23 2000 220.59
1988 226.95 2004 223.10
1992 225.00 2008 221.86
问题1 奥运会每4年举办一次,奥运会的游泳记录在不断地被突破,如男子400米自由泳项目,1996年奥运会冠军的成绩比1960年的提高了约30s。下面是该项目冠军的一些数据:
根据上面资料,你能否估计2012年伦敦奥运会时该项目的奥运会冠军成绩?
按照下面的步骤做,看能否预测出结果?
1、将数据在直角坐标系中描出。 2、观察这些点的特征,确定选用的函数形式,根据已知数据确定函数表达式。 3、检验。 4、应用此函数模型解题。
2012年伦敦奥运会中国选手孙杨以220.14s
的成绩打破男子400米自由泳项目的奥运会
纪录获得冠军,你预测的程度如何?
国际奥林匹克运动会早期,撑竿跳的记录近似地由下表给出:
动脑筋
年份 1900 1904 1908
高度(米) 3.33 3.53 3.73
观察这个表格中第二行的数据,可以为奥运会的撑杆跳高记录与时间的关系建立函数模型吗?
上表中每一届比上一届的记录提高了0.2米,可以试着建立一次函数的模型。
用t表示从1900年期增加的年份,则在奥与那会早期,撑杆跳高的记录y(米)与t的函数关系式为
y = kt + b
由于t=0(即1900年)时,长杆调高的记录为3.33米,t=4(即1904年)时,记录为3.53米,因此
b=3.33 ①
4k+b=3.35 ②
b=3.33 ①
4k+b=3.35 ②
把①代入②,得 4k+3.33=3.35
解得 k=0.05.
于是 y=0.05t+3.33. (D)
所以奥运会早期撑杆跳高记录y与时间t的函数关系式为:
y=0.05t+3.33.
你能利用公式(D)预测1912年奥运会的撑杆跳高记录吗?
做一做
y=0.05×12+3.33=3.93(米)
1912年奥运会撑杆跳高记录的却约为3.93米。这说明用所建立的函数模型,在已知数据邻近做预测,是与实际事实比较吻合的。
能够用公式(D)预测20世纪80年代,譬如1988年的奥运会撑杆跳高记录吗?
y=0.05×88+3.33=7.73(米)
实际上,1988年奥运会的撑杆跳高记录是6.06米,远低于7.73米。这表明用所建立的函数模型,原理已知数据作预测是不可靠的。
实验次数 第1次 第2次 第3次 第4次 第5次 第6次
下落高度/cm
反弹高度/cm
问题2 球从高处下落再反弹起来,可以直观地看出球的下落高度越高,反弹高度也就越高,那么球下落高度与反弹高度具有怎样的关系呢?请你进行实验,将实验数据填入下表,并根据实验数据建立球下落高度和反弹高度之间关系的函数模型。
1. 与同桌同学讨论,为什么用公式(D)预测1988年奥运会撑杆跳高记录高于实际记录?
练习
小明在练习100米短跑,今年1月至4月份的100米短跑成绩入校表所示:
练习
月份 1 2 3 4
成绩(秒)
1.56
1.54
1.52
15
(1)你能为小明的100米短跑成绩与时间的关系建立函数关系模型吗?
(2)用所求出的函数解析式预测小明今年6月份的100米短跑成绩。
(3)能用所求出的解析式预测小明明年12月份的100米短跑成绩吗?
同学们这节课有哪些收获?
建立函数模型的步骤: 1、将数据在直角坐标系中描出。 2、观察这些点的特征,确定选用的函数形式,根据已知数据确定函数表达式。 3、检验。 4、应用此函数模型解题。
