沪科版2021-2022学年度八年级数学上册 13.2.3命题与证明课件(共16张PPT)
文档属性
| 名称 | 沪科版2021-2022学年度八年级数学上册 13.2.3命题与证明课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 00:00:00 | ||
图片预览


文档简介
(共16张PPT)
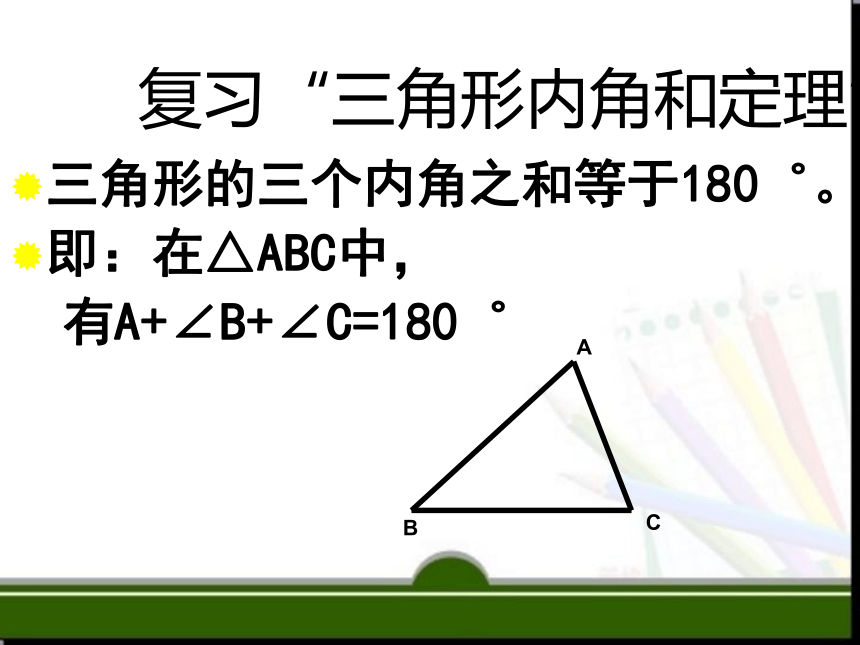
三角形的三个内角之和等于180゜。
即:在△ABC中,
有A+∠B+∠C=180゜
一、复习“三角形内角和定理”
A
B
C
二、论证“三角形内角和定理”
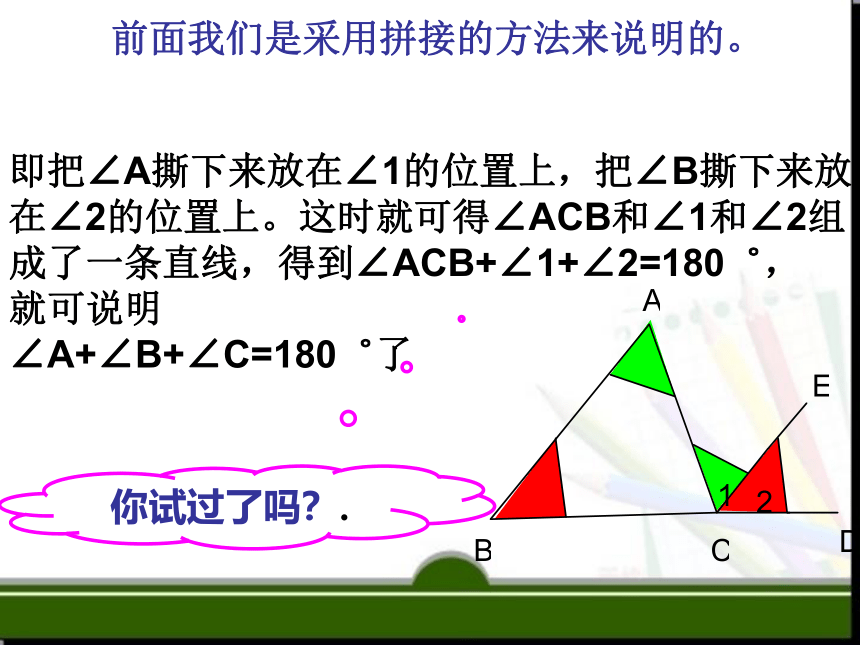
怎样验证三角形
的三个角的和等于180°呢??
即把∠A撕下来放在∠1的位置上,把∠B撕下来放在∠2的位置上。这时就可得∠ACB和∠1和∠2组成了一条直线,得到∠ACB+∠1+∠2=180゜,
就可说明
∠A+∠B+∠C=180゜了
你试过了吗?.
前面我们是采用拼接的方法来说明的。
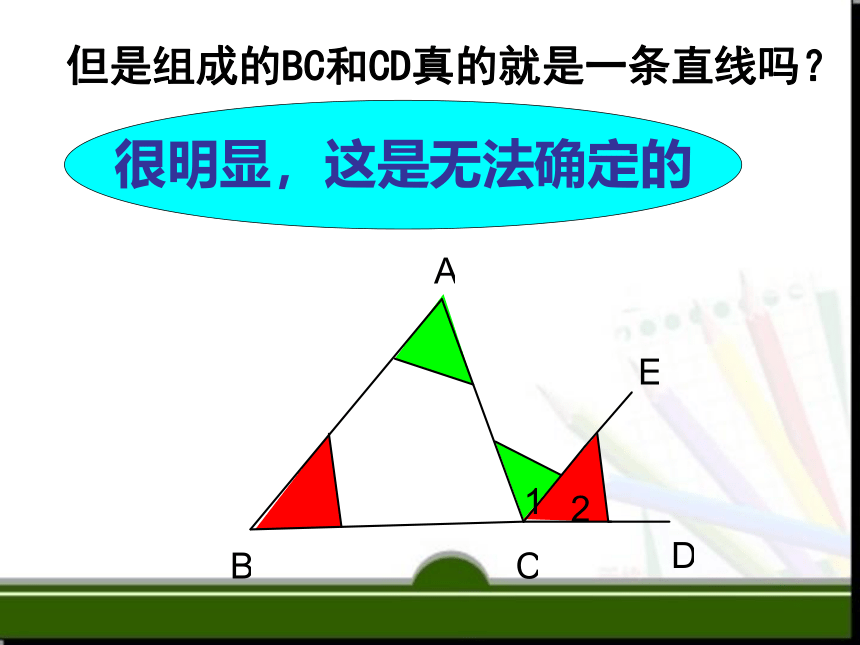
但是组成的BC和CD真的就是一条直线吗?
很明显,这是无法确定的
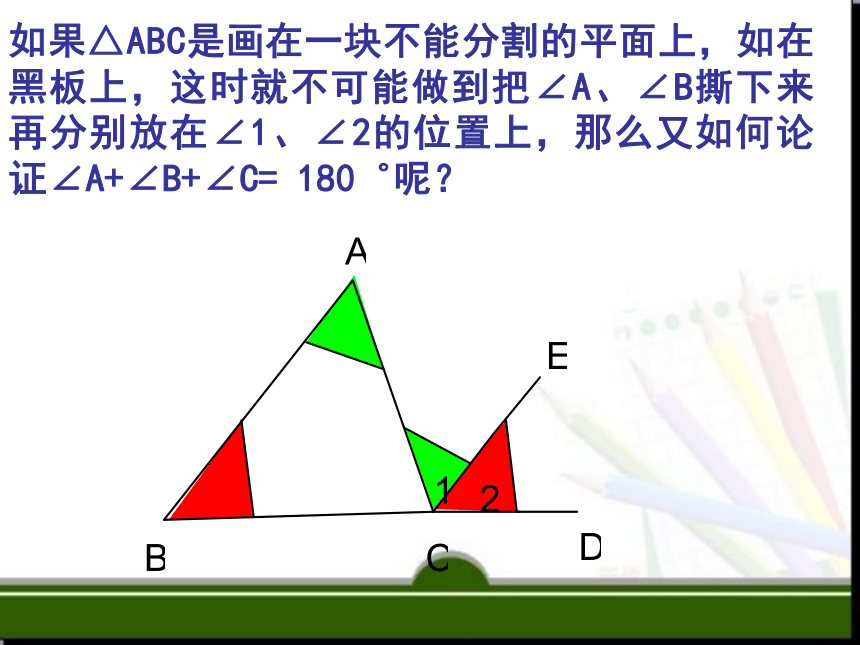
如果△ABC是画在一块不能分割的平面上,如在黑板上,这时就不可能做到把∠A、∠B撕下来再分别放在∠1、∠2的位置上,那么又如何论证∠A+∠B+∠C= 180゜呢?
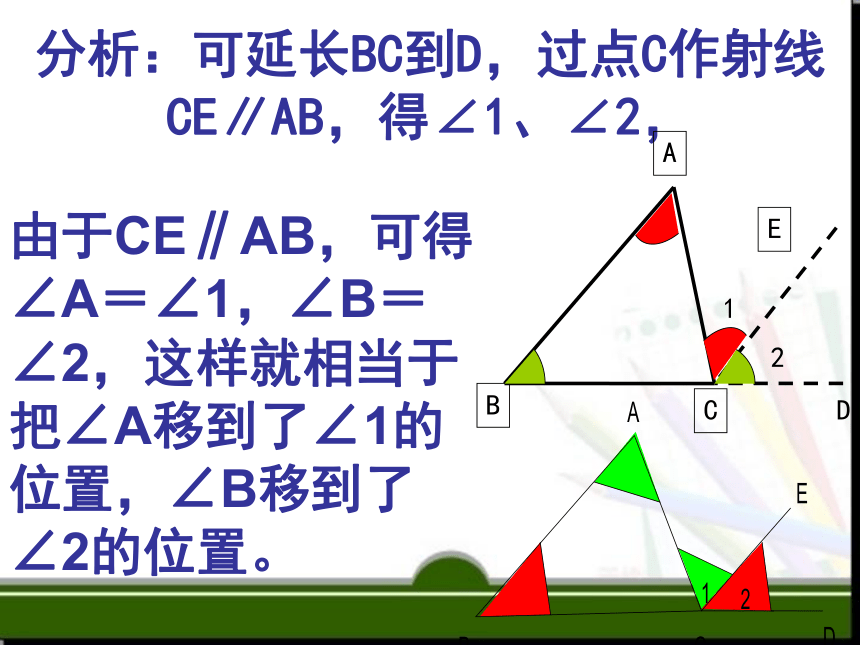
分析:可延长BC到D,过点C作射线CE∥AB,得∠1、∠2,
B
A
C
D
E
1
2
由于CE∥AB,可得∠A=∠1,∠B=∠2,这样就相当于把∠A移到了∠1的位置,∠B移到了∠2的位置。
∠2=∠B(两直线平行, )
∴ (两直线平行,内错角相等)
又∵∠ACB+∠1+∠2=180゜( )
证明:延长BC到D,过点C作射线CE∥AB,
∵CE∥AB(作图)
这里的CD,CE称为辅助线,通常辅助线画成虚线
B
A
C
D
E
1
2
∠1=∠A
同位角相等
平角定义
∴∠A+∠B+∠C=180゜(等量代换)
A
B
C
A
B
C
E
D
A
B
C
E
E
D
F
关于辅助线
1.辅助线是为了证明的需要,在原来图形上添画的线.(辅助线通常画成虚线)
2.它的作用是把分散的条件集中,把隐含
的条件显现出来,起到牵线搭桥的作用.
3.添加辅助线,可构造新图形,形成新关系,找到联系已知与未知的桥梁,把问题
转化,但辅助线的添法没有一定的规律,
要根据需要而定,平时做题时要注意总结.
证明:直角三角形两个锐角互余。
求证:∠A+∠B=90°.
已知:如图,△ABC中,∠C=90°.
证明:∵∠A+∠B+∠C=180°,(三角形的
内角和定理)
∴ ∠A+∠B=180°-∠C.
又∵ ∠C=90°,
∴ ∠A+∠B=180°- 90°= 90°.
课堂练习
如果一个三角形中一个角为90°, 根据三角形内角和定理,另两个角的和应为90°,于是得
推论1 直角三角形的两锐角互余.
在这里,我们通过三角形内角和定理直接推导出两个新定理.像这样,由基本事实或定理直接推出的真命题,叫做推论.
推论2 有两个角互余的三角形是直角三角形.
四边形的内角和等于多少度?证明你的结论.
已知:四边形ABCD
求证:∠A+∠B+∠C+∠D=360°.
证明:
连接AC
∵∠1+∠2+∠D=180°,
∠ 3+∠4+∠B=180°,(三角形的内角和定理)
A
B
C
D
⌒
⌒
⌒
2
⌒
1
3
4
∴∠1+∠2+∠D+∠3+∠4+∠B=360°.
又∵ ∠DAB=∠1+∠3,∠DCB=∠2+∠4 ,
∴ ∠DAB+ ∠B+ ∠DCB+∠D= 360°.(等量代换)
即四边形的内角和等于360°.
课堂练习
作业:请同学们回去想想证明三角形内角和为180°的证明方法,越多越好!看谁想的方法最多!
三角形的三个内角之和等于180゜。
即:在△ABC中,
有A+∠B+∠C=180゜
一、复习“三角形内角和定理”
A
B
C
二、论证“三角形内角和定理”
怎样验证三角形
的三个角的和等于180°呢??
即把∠A撕下来放在∠1的位置上,把∠B撕下来放在∠2的位置上。这时就可得∠ACB和∠1和∠2组成了一条直线,得到∠ACB+∠1+∠2=180゜,
就可说明
∠A+∠B+∠C=180゜了
你试过了吗?.
前面我们是采用拼接的方法来说明的。
但是组成的BC和CD真的就是一条直线吗?
很明显,这是无法确定的
如果△ABC是画在一块不能分割的平面上,如在黑板上,这时就不可能做到把∠A、∠B撕下来再分别放在∠1、∠2的位置上,那么又如何论证∠A+∠B+∠C= 180゜呢?
分析:可延长BC到D,过点C作射线CE∥AB,得∠1、∠2,
B
A
C
D
E
1
2
由于CE∥AB,可得∠A=∠1,∠B=∠2,这样就相当于把∠A移到了∠1的位置,∠B移到了∠2的位置。
∠2=∠B(两直线平行, )
∴ (两直线平行,内错角相等)
又∵∠ACB+∠1+∠2=180゜( )
证明:延长BC到D,过点C作射线CE∥AB,
∵CE∥AB(作图)
这里的CD,CE称为辅助线,通常辅助线画成虚线
B
A
C
D
E
1
2
∠1=∠A
同位角相等
平角定义
∴∠A+∠B+∠C=180゜(等量代换)
A
B
C
A
B
C
E
D
A
B
C
E
E
D
F
关于辅助线
1.辅助线是为了证明的需要,在原来图形上添画的线.(辅助线通常画成虚线)
2.它的作用是把分散的条件集中,把隐含
的条件显现出来,起到牵线搭桥的作用.
3.添加辅助线,可构造新图形,形成新关系,找到联系已知与未知的桥梁,把问题
转化,但辅助线的添法没有一定的规律,
要根据需要而定,平时做题时要注意总结.
证明:直角三角形两个锐角互余。
求证:∠A+∠B=90°.
已知:如图,△ABC中,∠C=90°.
证明:∵∠A+∠B+∠C=180°,(三角形的
内角和定理)
∴ ∠A+∠B=180°-∠C.
又∵ ∠C=90°,
∴ ∠A+∠B=180°- 90°= 90°.
课堂练习
如果一个三角形中一个角为90°, 根据三角形内角和定理,另两个角的和应为90°,于是得
推论1 直角三角形的两锐角互余.
在这里,我们通过三角形内角和定理直接推导出两个新定理.像这样,由基本事实或定理直接推出的真命题,叫做推论.
推论2 有两个角互余的三角形是直角三角形.
四边形的内角和等于多少度?证明你的结论.
已知:四边形ABCD
求证:∠A+∠B+∠C+∠D=360°.
证明:
连接AC
∵∠1+∠2+∠D=180°,
∠ 3+∠4+∠B=180°,(三角形的内角和定理)
A
B
C
D
⌒
⌒
⌒
2
⌒
1
3
4
∴∠1+∠2+∠D+∠3+∠4+∠B=360°.
又∵ ∠DAB=∠1+∠3,∠DCB=∠2+∠4 ,
∴ ∠DAB+ ∠B+ ∠DCB+∠D= 360°.(等量代换)
即四边形的内角和等于360°.
课堂练习
作业:请同学们回去想想证明三角形内角和为180°的证明方法,越多越好!看谁想的方法最多!
