2021-2022学年度沪科版八年级数学上册课件 14.2.三角形全等的判定(第4课时)(共15张PPT)
文档属性
| 名称 | 2021-2022学年度沪科版八年级数学上册课件 14.2.三角形全等的判定(第4课时)(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 795.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
Page *
Page *我们知道,SAS、ASA、SSS都可以作为判定两个三角形全等的条件.其实,在三角形的六个基本元素中选择三个元素对应相等,出了可以配成SAS、ASA、SSS外,还可以配成:AAA、SSA、AAS.
想一想: AAA、SSA、AAS能判定这两个三角形全等吗?
AAA、SSA是不能判定这两个三角形全等的。下面就让我们来探究一下AAS。
A
B
C
A ′
B ′
C ′
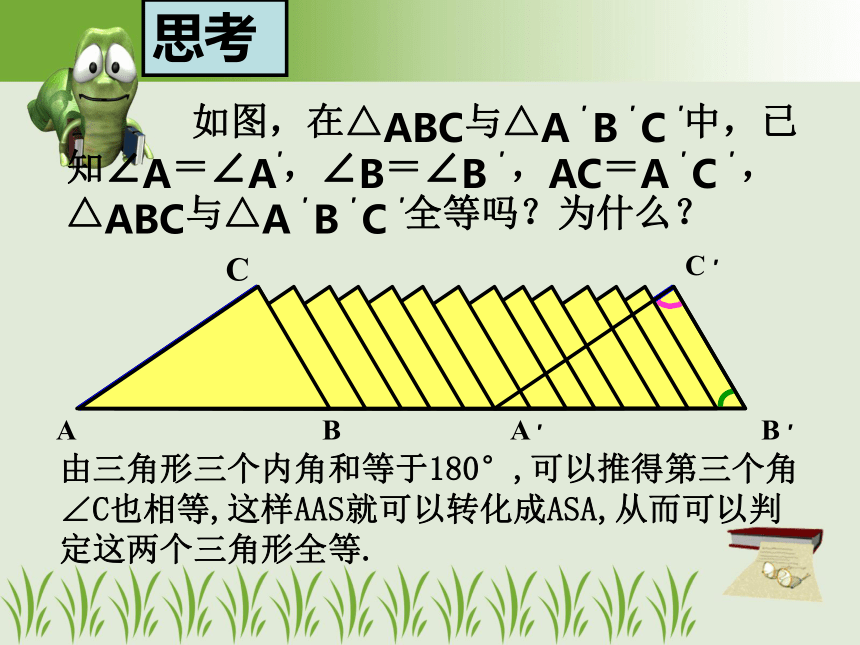
思考
如图,在△ABC与△A ′ B ′ C ′中,已知∠A=∠A′,∠B=∠B ′ ,AC=A ′ C ′ , △ABC与△A ′ B ′ C ′全等吗?为什么?
由三角形三个内角和等于180°,可以推得第三个角∠C也相等,这样AAS就可以转化成ASA,从而可以判定这两个三角形全等.
Page *
两个角及其中一个角的对边对应相等的两个三角形全等.简记为 “角角边”或AAS.
Page *
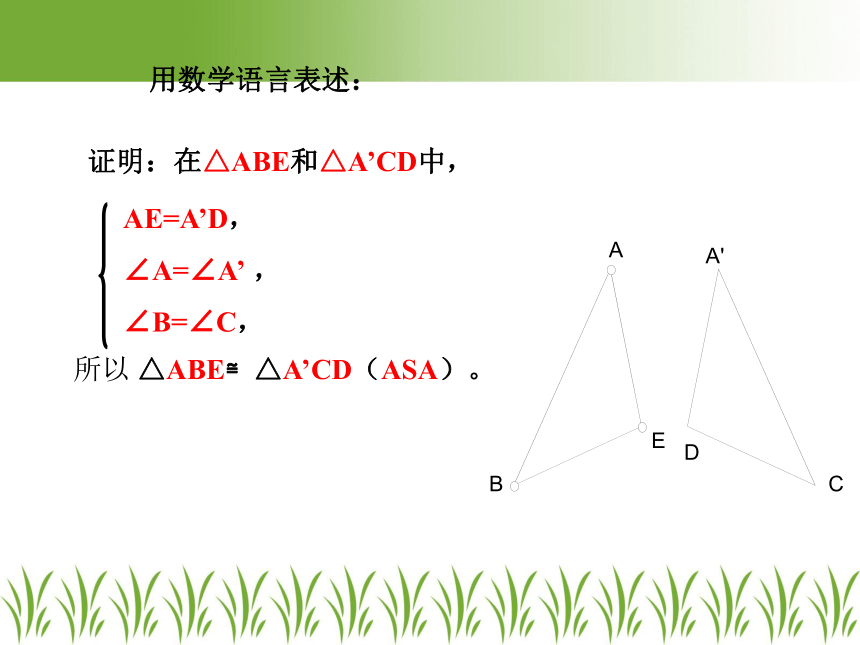
AE=A’D,
∠A=∠A’ ,
∠B=∠C,
证明:在△ABE和△A’CD中,
所以 △ABE≌△A’CD(ASA)。
用数学语言表述:
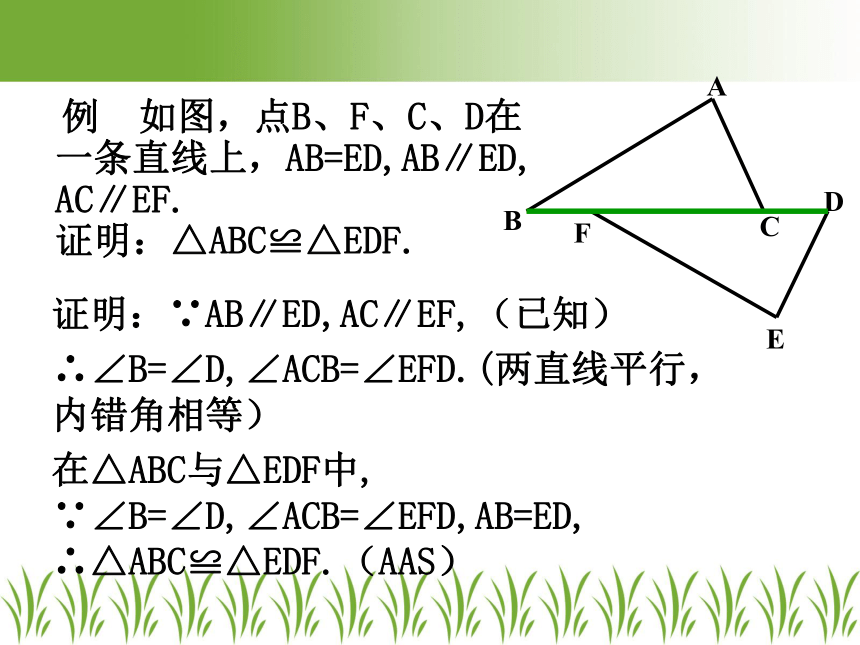
例 如图,点B、F、C、D在 一条直线上,AB=ED,AB∥ED, AC∥EF. 求证:△ABC≌△EDF.
D
A
B
C
E
F
例 如图,点B、F、C、D在 一条直线上,AB=ED,AB∥ED, AC∥EF. 证明:△ABC≌△EDF.
证明:∵AB∥ED,AC∥EF,(已知)
∴∠B=∠D,∠ACB=∠EFD.(两直线平行,内错角相等)
在△ABC与△EDF中,
∵∠B=∠D,∠ACB=∠EFD,AB=ED,
∴△ABC≌△EDF.(AAS)
D
A
B
C
E
F
例2 证明:全等三角形对应边上的高相等.
已知:如图, △ABC≌△ A′B′C′.AD、A′D′分别是△ABC和△ A′B′C′的高.求证:AD=A′D′.
证明:∵ △ABC≌△ A′B′C′,(已知)
∴ AB=A′B′,∠B=∠B′.(全等三角形的对应边、对应角相等)
∵ ∠ADB=∠A′D′B′=90°.(垂直定义)
在△ABD和△ A′B′D′中,
∵ ∠B=∠B′, ∠ADB=∠A′D′B′, AB=A′B′,
∴ △ABD≌△ A′B′D′.(AAS)
∴ AD=A′D′.(全等三角形的对应边相等)
A
B
C
D
A′
B′
C′
D′
例2 证明:全等三角形对应边上的高相等.
已知:如图, △ABC≌△ A′B′C′.AD、A′D′分别是△ABC和△ A′B′C′的高.求证:AD=A′D′.
A
B
C
D
A′
B′
C′
D′
2
1
如图,已知∠1=∠2,∠A=∠D,
试说明△ABC与△DBC全等的理由.
D
A
B
C
1
解:在△ABC和△DBC中,
∠1=∠2,(已知)
∠A=∠D,(已知)
BC=BC,(公共边)
∴△ABC≌△DBC . (AAS)
2
练习1
如图,已知AB与CD相交于O,∠A=∠D,CO=BO,试说明△AOC与△DOB全等的理由.
D
解:在△AOC和△DOB中,
∠1=∠2,(对顶角相等)
∠A=∠D,(已知)
CO=BO,(已知)
∴△AOC≌△DOB . ( AAS)
练习2
A
C
B
O
1
2
如图,∠1=∠2,∠C=∠D
求证:AC=AD
在△ABD和△ABC中,
∠1=∠2 (已知),
∠D=∠C(已知),
AB=AB(公共边),
所以△ABD≌△ABC (AAS)。
所以AC=AD(全等三角形对应边相等)。
证明:
1
2
练习3
试比较ASA与AAS两个判定之间的区别与联系。
思考
ASA与AAS都要求有两个角一条边对应相等。
ASA是两角一夹边而AAS是两角一对边。
联系:
区别:
小结
1
2
两个角及其中一个角的对边对应相等的两个三角形全等.简记为“角角边”或“AAS”.
三角形全等判定的两个方法ASA与AAS有哪些区别和联系。
Page *
再见!
课后要好好总结哦!
学而不思则罔,思而不学则殆。
——孔子
Page *
Page *
Page *我们知道,SAS、ASA、SSS都可以作为判定两个三角形全等的条件.其实,在三角形的六个基本元素中选择三个元素对应相等,出了可以配成SAS、ASA、SSS外,还可以配成:AAA、SSA、AAS.
想一想: AAA、SSA、AAS能判定这两个三角形全等吗?
AAA、SSA是不能判定这两个三角形全等的。下面就让我们来探究一下AAS。
A
B
C
A ′
B ′
C ′
思考
如图,在△ABC与△A ′ B ′ C ′中,已知∠A=∠A′,∠B=∠B ′ ,AC=A ′ C ′ , △ABC与△A ′ B ′ C ′全等吗?为什么?
由三角形三个内角和等于180°,可以推得第三个角∠C也相等,这样AAS就可以转化成ASA,从而可以判定这两个三角形全等.
Page *
两个角及其中一个角的对边对应相等的两个三角形全等.简记为 “角角边”或AAS.
Page *
AE=A’D,
∠A=∠A’ ,
∠B=∠C,
证明:在△ABE和△A’CD中,
所以 △ABE≌△A’CD(ASA)。
用数学语言表述:
例 如图,点B、F、C、D在 一条直线上,AB=ED,AB∥ED, AC∥EF. 求证:△ABC≌△EDF.
D
A
B
C
E
F
例 如图,点B、F、C、D在 一条直线上,AB=ED,AB∥ED, AC∥EF. 证明:△ABC≌△EDF.
证明:∵AB∥ED,AC∥EF,(已知)
∴∠B=∠D,∠ACB=∠EFD.(两直线平行,内错角相等)
在△ABC与△EDF中,
∵∠B=∠D,∠ACB=∠EFD,AB=ED,
∴△ABC≌△EDF.(AAS)
D
A
B
C
E
F
例2 证明:全等三角形对应边上的高相等.
已知:如图, △ABC≌△ A′B′C′.AD、A′D′分别是△ABC和△ A′B′C′的高.求证:AD=A′D′.
证明:∵ △ABC≌△ A′B′C′,(已知)
∴ AB=A′B′,∠B=∠B′.(全等三角形的对应边、对应角相等)
∵ ∠ADB=∠A′D′B′=90°.(垂直定义)
在△ABD和△ A′B′D′中,
∵ ∠B=∠B′, ∠ADB=∠A′D′B′, AB=A′B′,
∴ △ABD≌△ A′B′D′.(AAS)
∴ AD=A′D′.(全等三角形的对应边相等)
A
B
C
D
A′
B′
C′
D′
例2 证明:全等三角形对应边上的高相等.
已知:如图, △ABC≌△ A′B′C′.AD、A′D′分别是△ABC和△ A′B′C′的高.求证:AD=A′D′.
A
B
C
D
A′
B′
C′
D′
2
1
如图,已知∠1=∠2,∠A=∠D,
试说明△ABC与△DBC全等的理由.
D
A
B
C
1
解:在△ABC和△DBC中,
∠1=∠2,(已知)
∠A=∠D,(已知)
BC=BC,(公共边)
∴△ABC≌△DBC . (AAS)
2
练习1
如图,已知AB与CD相交于O,∠A=∠D,CO=BO,试说明△AOC与△DOB全等的理由.
D
解:在△AOC和△DOB中,
∠1=∠2,(对顶角相等)
∠A=∠D,(已知)
CO=BO,(已知)
∴△AOC≌△DOB . ( AAS)
练习2
A
C
B
O
1
2
如图,∠1=∠2,∠C=∠D
求证:AC=AD
在△ABD和△ABC中,
∠1=∠2 (已知),
∠D=∠C(已知),
AB=AB(公共边),
所以△ABD≌△ABC (AAS)。
所以AC=AD(全等三角形对应边相等)。
证明:
1
2
练习3
试比较ASA与AAS两个判定之间的区别与联系。
思考
ASA与AAS都要求有两个角一条边对应相等。
ASA是两角一夹边而AAS是两角一对边。
联系:
区别:
小结
1
2
两个角及其中一个角的对边对应相等的两个三角形全等.简记为“角角边”或“AAS”.
三角形全等判定的两个方法ASA与AAS有哪些区别和联系。
Page *
再见!
课后要好好总结哦!
学而不思则罔,思而不学则殆。
——孔子
Page *
