2021-2022学年度沪科版八年级数学上册课件 14.2三角形全等的判定(第3课时)(共17张PPT)
文档属性
| 名称 | 2021-2022学年度沪科版八年级数学上册课件 14.2三角形全等的判定(第3课时)(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 864.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
14.2 三角形全等的判定
(第3课时)
回顾与思考:
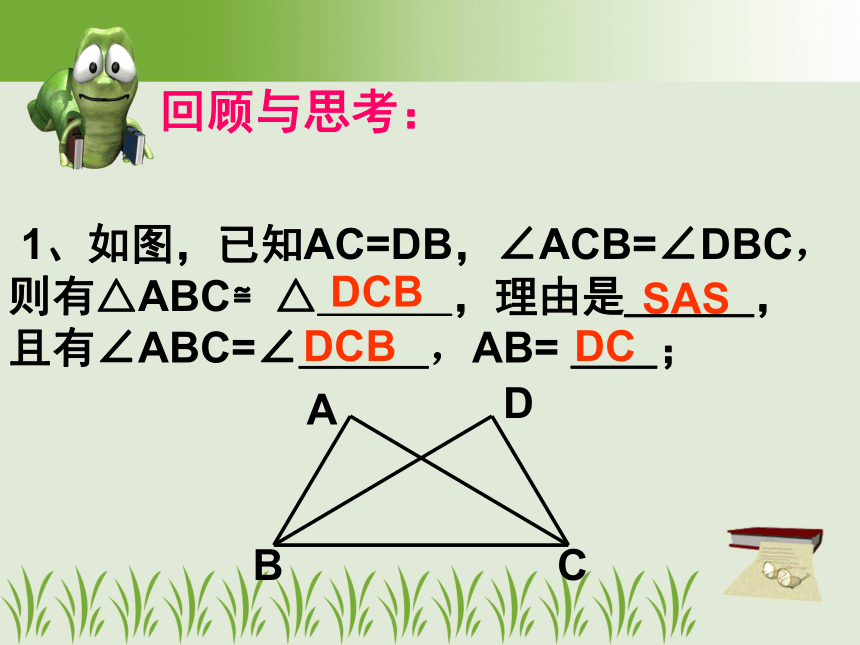
1、如图,已知AC=DB,∠ACB=∠DBC,则有△ABC≌△____,理由是___,
且有∠ABC=∠___,AB= __;
DCB
SAS
DCB
DC
A
B
C
D
2、如图,已知AD平分∠BAC,
要使△ABD≌△ACD,
根据“SAS”需要添加条件_______;
根据“ASA”需要添加条件_______。
A
B
C
D
AB=AC
∠BDA=∠CDA
⒈用长度分别为5cm、6cm、7cm小棒搭一个三角形,与周围同学比较一下,你们所搭的三角形是否都全等。
⒉用一根长20cm的铁丝,围成一个三角形,怎样才能使你和同学围成的三角形全等?
⒊按下列画法,用圆规和刻度尺画一个三角形: (1)画线段AB=5cm; (2)分别以点A、B为圆心,4cm、7cm的长为半径画弧,两弧相交于点C; (3)连接AC、BC。
你所画的三角形与同学画的三角形全等吗?
做一做
三边对应相等的两个三角形全等,简记为“边边边”或“SSS”。
A
B
C
〃
\
≡
D
E
F
〃
\
≡
在△ABC和△DEF中,
AB=DE,
BC=EF,
AC=DF,
△ABC≌△DEF.(SSS)
上面的结论告诉我们,如果一个三角形三边的长度确定,那么这个三角形的形状和大小就完全确定。如左图是用3根木条钉成的框架,它的形状和大小完全确定。
三角形的这种性质叫做:三角形的稳定性
如右图四边形是否具有稳定性?
四边形和其它多边形都不具有稳定性
四边形不具有稳定性,你能想出什么方法让它们的形状不发生改变吗
试一试
例 已知:如图,点B、E、C、F在同一直线上,AB=DE,AC=DF,BE=CF.求证:AB∥DE,AC∥DF.
A
B
C
D
E
F
证明:∵BE=CF,(已知)
∴BE+EC=CF+CE,(等式的性质)
即BC=EF.
在△ABC和△DEF中,
∵AB=DE,AC=DF,BC=EF,
∴△ABC≌△DEF.(SSS)
∴∠B=∠DEF, ∠ACB=∠F.(全等三角形的对应角相等)
∴AB∥DE,AC∥DF.(同位角相等,两直线平行)
例 已知:如图,点B、E、C、F在同一直线上,AB=DE,AC=DF,BE=CF.求证:AB∥DE,AC∥DF.
A
B
C
D
E
F
1、如图,AB=DC,AC=DB,△ABC与△DCB全等吗?为什么?
A
B
C
D
O
解:△ABC≌△DCB, 因为AB=DC,AC=DB,BC=CB, 根据“SSS”,可以得到△ABC≌△DCB
那么△ABO与△DCO全等吗?
2、如图,△ABC中,AB=AC,AD是BC边上的中线,则∠BDA=__度,为什么?
A
D
C
B
解:因为AD是BC边上的中线, 所以BD=CD.
所以∠BDA=∠CDA. 因为∠BDA+∠CDA=180O , 所以∠BDA=∠CDA=180O÷2=900.
90
BD=CD,
AB=AC,
AD=AD,
所以△ABD≌△ACD.(SSS)
在△ABD和△ACD中,因为
3、如图,方格纸中△DEF的三个顶点分别在小正方形的顶点(格点)上,请你在图中再画一个顶点都在格点上的△ABC,且使△ABC≌△DEF。
D
E
F
D
E
F
D
E
F
A
B
C
A
B
C
B
A
C
4、如图,△ABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形,使所作三角形,与△ABC全等,这样的三角形最多可以画出几个?
5、如图,AB=AC,AE=AD,BD=CE,求证:△AEB ≌ △ ADC。
证明:∵BD=CE
∴ BD-ED=CE-ED,即BE=CD。
在AEB和ADC中,
AB=AC
AE=AD
BE=CD
∴ △AEB ≌ △ ADC
C
A
B
D
E
小结:
1.已知三边长,会用直尺和圆规作三角形。
2.了解了三角形的稳定性,及其在生产和生活中的广泛应用。
3 .善于从题意中找出条件,要注意充分利用隐含条件.如公共边,公共角,对顶角等.
14.2 三角形全等的判定
(第3课时)
回顾与思考:
1、如图,已知AC=DB,∠ACB=∠DBC,则有△ABC≌△____,理由是___,
且有∠ABC=∠___,AB= __;
DCB
SAS
DCB
DC
A
B
C
D
2、如图,已知AD平分∠BAC,
要使△ABD≌△ACD,
根据“SAS”需要添加条件_______;
根据“ASA”需要添加条件_______。
A
B
C
D
AB=AC
∠BDA=∠CDA
⒈用长度分别为5cm、6cm、7cm小棒搭一个三角形,与周围同学比较一下,你们所搭的三角形是否都全等。
⒉用一根长20cm的铁丝,围成一个三角形,怎样才能使你和同学围成的三角形全等?
⒊按下列画法,用圆规和刻度尺画一个三角形: (1)画线段AB=5cm; (2)分别以点A、B为圆心,4cm、7cm的长为半径画弧,两弧相交于点C; (3)连接AC、BC。
你所画的三角形与同学画的三角形全等吗?
做一做
三边对应相等的两个三角形全等,简记为“边边边”或“SSS”。
A
B
C
〃
\
≡
D
E
F
〃
\
≡
在△ABC和△DEF中,
AB=DE,
BC=EF,
AC=DF,
△ABC≌△DEF.(SSS)
上面的结论告诉我们,如果一个三角形三边的长度确定,那么这个三角形的形状和大小就完全确定。如左图是用3根木条钉成的框架,它的形状和大小完全确定。
三角形的这种性质叫做:三角形的稳定性
如右图四边形是否具有稳定性?
四边形和其它多边形都不具有稳定性
四边形不具有稳定性,你能想出什么方法让它们的形状不发生改变吗
试一试
例 已知:如图,点B、E、C、F在同一直线上,AB=DE,AC=DF,BE=CF.求证:AB∥DE,AC∥DF.
A
B
C
D
E
F
证明:∵BE=CF,(已知)
∴BE+EC=CF+CE,(等式的性质)
即BC=EF.
在△ABC和△DEF中,
∵AB=DE,AC=DF,BC=EF,
∴△ABC≌△DEF.(SSS)
∴∠B=∠DEF, ∠ACB=∠F.(全等三角形的对应角相等)
∴AB∥DE,AC∥DF.(同位角相等,两直线平行)
例 已知:如图,点B、E、C、F在同一直线上,AB=DE,AC=DF,BE=CF.求证:AB∥DE,AC∥DF.
A
B
C
D
E
F
1、如图,AB=DC,AC=DB,△ABC与△DCB全等吗?为什么?
A
B
C
D
O
解:△ABC≌△DCB, 因为AB=DC,AC=DB,BC=CB, 根据“SSS”,可以得到△ABC≌△DCB
那么△ABO与△DCO全等吗?
2、如图,△ABC中,AB=AC,AD是BC边上的中线,则∠BDA=__度,为什么?
A
D
C
B
解:因为AD是BC边上的中线, 所以BD=CD.
所以∠BDA=∠CDA. 因为∠BDA+∠CDA=180O , 所以∠BDA=∠CDA=180O÷2=900.
90
BD=CD,
AB=AC,
AD=AD,
所以△ABD≌△ACD.(SSS)
在△ABD和△ACD中,因为
3、如图,方格纸中△DEF的三个顶点分别在小正方形的顶点(格点)上,请你在图中再画一个顶点都在格点上的△ABC,且使△ABC≌△DEF。
D
E
F
D
E
F
D
E
F
A
B
C
A
B
C
B
A
C
4、如图,△ABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形,使所作三角形,与△ABC全等,这样的三角形最多可以画出几个?
5、如图,AB=AC,AE=AD,BD=CE,求证:△AEB ≌ △ ADC。
证明:∵BD=CE
∴ BD-ED=CE-ED,即BE=CD。
在AEB和ADC中,
AB=AC
AE=AD
BE=CD
∴ △AEB ≌ △ ADC
C
A
B
D
E
小结:
1.已知三边长,会用直尺和圆规作三角形。
2.了解了三角形的稳定性,及其在生产和生活中的广泛应用。
3 .善于从题意中找出条件,要注意充分利用隐含条件.如公共边,公共角,对顶角等.
