人教新课标A版选修2-1 第三章 空间向量与立体几何 单元练习(Word含答案解析)
文档属性
| 名称 | 人教新课标A版选修2-1 第三章 空间向量与立体几何 单元练习(Word含答案解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 412.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览


文档简介
人教新课标A版选修2-1
第三章 空间向量与立体几何
一、单选题
1.已知 , ,向量 在 方向上的投影是4,则 =( )
A. 8 B. 12 C. -8 D. 2
2.如图,在四面体VABC中,已知VA⊥平面VBC,VA与平面ABC所成的角为45°,D是BC上一动点,设直线VD与平面ABC所成的角为θ,则( )
A. θ≤60° B. θ≥30° C. θ≤45° D. θ≤75°
3.已知向量 , ,则以 , 为邻边的三角形 的面积( )
A. B. C. 2 D. 4
4.如图,在长方体 中,M,N分别是棱BB1 , B1C1的中点,若∠CMN=90°,则异面直线AD1和DM所成角为( )
A. 30° B. 45° C. 60° D. 90°
5.已知 , , 与 的夹角为 , 是与向量 方向相同的单位向量,则 在向量 上的投影向量为( )
A. B. C. D.
6.三棱锥 中, 底面ABC, , ,D为AB的中点, ,则点D到面 的距离等于( )
A. B. C. D.
7.如图所示,平面 平面 ,二面角 ,已知 , ,直线 与平面 ,平面 所成角均为 ,与 所成角为 ,若 ,则 的最大值是( )
A. B. C. D.
8.在矩形ABCD中,AB=2BC=2,点P在CD边上运动(如图甲),现以AP为折痕将 折起,使得点D在平面ABCP内的射影 恰好落在AB边上(如图乙).设 二面角D-AP-B的余弦值为 ,则函数 的图象大致是( )
B.
C. D.
9.设A为平面 上一点,过点A的直线AO在 平面上的射影为AB,AC为 平面内的一条直线,令 , , ,则这三个角存在一个余弦关系: (其中 和 只能是锐角),称为最小张角定理.直线l与平面 所成的角是 ,若直线l在 内的射影与 内的直线m所成角为 ,则直线l与直线m所成的角是( )
A. B. C. D.
10.正四面体 中, 在平面 内,点 是线段 的中点,在该四面体绕 旋转的过程中,直线 与平面 所成角的余弦值不可能是( )
A. B. C. D. 1
二、填空题
11.向量 =(1,2,-1), =(2,1,a),若 ,则a=________.
12.在空间直角坐标系 中,已知 , ,则向量 与平面 的法向量的夹角的正弦值为________.
13.已知矩形 , ,沿 翻折,使面 ⊥面 ,则二面角 的余弦值为________.
14.若点M在平面 外,过点M作面 的垂线,则称垂足N为点M在平面 内的正投影,记为 .如图,在棱长为 的正方体 中,记平面 为 ,平面 为 ,点 是棱 上一动点(与 不重合), , .给出下列三个结论:①线段 长度的取值范围是 ;②存在点 使得 平面 ;③存在点 使得 .其中正确结论的序号是________.
15.《九章算术》中的“邪田”意为直角梯形,上、下底称为畔,高称为正广,非高腰边称为邪.在四棱锥 中,底面 为邪田,两畔 分别为 ,正广 为 , 平面 ,邪所在直线与平面 所成角的大小为 .
16.在平面五边形 中, , , , ,且 .将五边形 沿对角线 折起,使平面 与平面 所成的二面角为 ,则沿对角线 折起后所得几何体的外接球的表面积是________.
17.斜线 与平面 成15°角,斜足为 , 为 在 内的射影, 为 的中点, 是 内过点 的动直线,若 上存在点 , 使 ,则 则的最大值是________,此时二面角 平面角的正弦值是________
18.设三棱锥 的底面是正三角形,侧棱长均相等, 是棱 上的点(不含端点),记直线 与直线 所成的角为 ,直线 与平面 所成的角为 ,二面角 的平面角为 ,则三个角 、 、 中最小的角是________.
三、解答题
19.四棱锥 中, , , ,平面 平面 ,点 为 的中点.
(1)求证:向量 、 、 共面;
(2)若 ,求二面角 的余弦值.
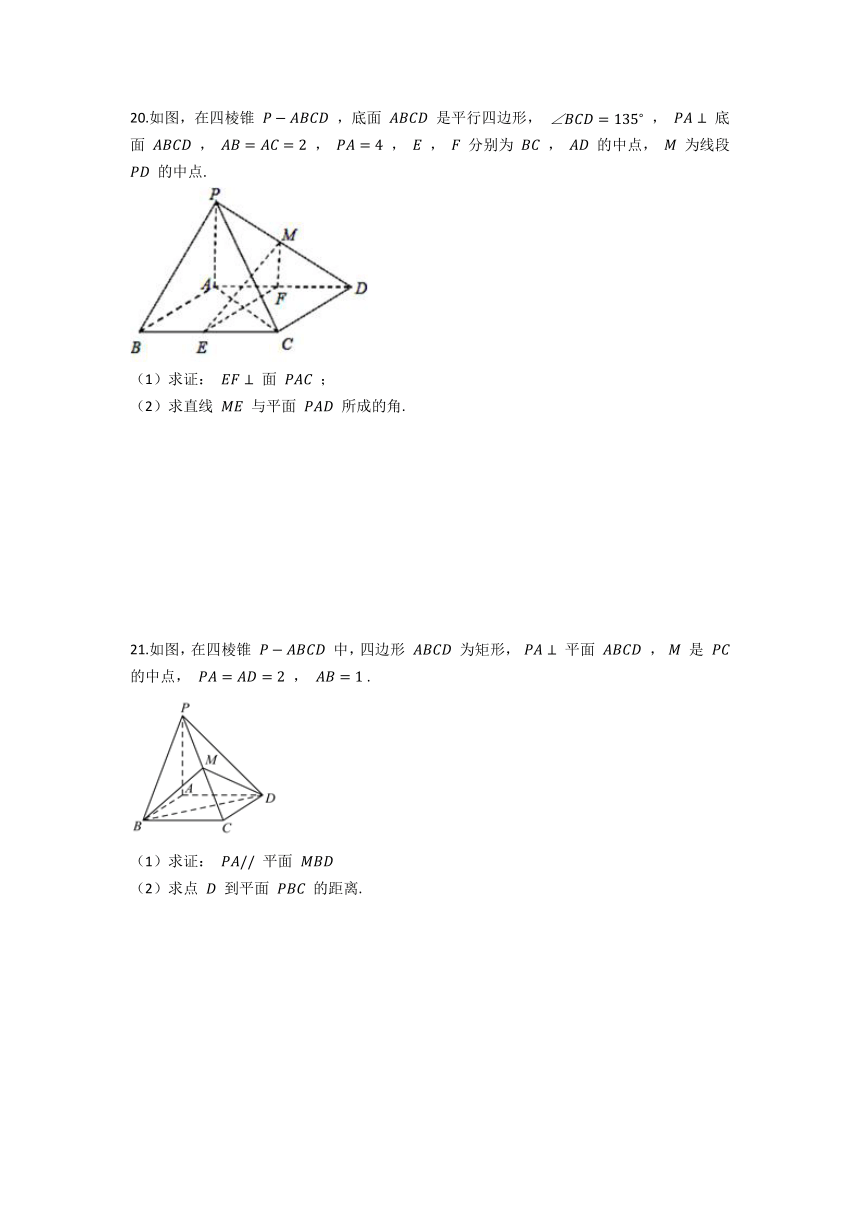
20.如图,在四棱锥 ,底面 是平行四边形, , 底面 , , , , 分别为 , 的中点, 为线段 的中点.
(1)求证: 面 ;
(2)求直线 与平面 所成的角.
21.如图,在四棱锥 中,四边形 为矩形, 平面 , 是 的中点, , .
(1)求证: 平面
(2)求点 到平面 的距离.
22.如图,在四棱锥 中, 底面 , , , , ,点 为棱 的中点.
(1)证明: ;
(2)求直线 与平面 所成角的正弦值;
(3)若 为棱 上一点,满足 ,求二面角 的余弦值.
答案解析部分
一、单选题
1.【答案】 B
【解析】解: 由题意知向量 在 方向上的投影是4,即 ,
则
故答案为:B
【分析】根据向量的投影,结合向量的数量积,直接求解即可.
2.【答案】 C
【解析】如图,作 底面 于点 , 于 ,由几何关系可得, , ,当 固定时, 也固定, 最小时应为 时,此时 与 重合,又因为VA⊥平面VBC,所以 ,所以 平面 ,易知 三点共线,因为VA与平面ABC所成的角为45°,故 , VA⊥平面VBC,所以 ,所以 ,此时 最大, 最大,故 .
故答案为:C
【分析】先分析出线面角取得最大值的条件,再求出线面角的最大值,即可得出答案。
3.【答案】 B
【解析】因为向量 , ,
所以 , ,
,
因此 ,
所以,以 , 为邻边的三角形 的面积为 .
故答案为:B.
【分析】根据向量夹角的坐标表示,向量模的坐标表示,先求出 ,以及向量的模,再得出 ,根据三角形面积公式,即可得出结果.
4.【答案】 D
【解析】以 为坐标原点, 所在直线分别为 轴,建立空间直角坐标系,如图,
设 ,则 , ,
,
因为 ,所以 ,即有 .
因为 ,所以 ,即异面直线 和 所成角为 .
故答案为:D.
【分析】建立空间直角坐标系,结合 ,求出 的坐标,利用向量夹角公式可求.
5.【答案】 A
【解析】 , , 与 的夹角为 ,
则 ,
,
所以,向量 在向量 方向上的投影为 ,
是与向量 方向相同的单位向量,因此, 在向量 上的投影向量为 .
故答案为:A.
【分析】计算出向量 在向量 方向上的投影 的值,进而可得出 在向量 上的投影向量.
6.【答案】 C
【解析】如图,
在三角形 中,过A作AE⊥SB交SB于E,
因为 面 ,所以 ,又 , ,所以 面 ,因为 面 ,所以 ,而AE⊥SB,且 ,所以AE⊥面SBC.
在三角形SAB中,由勾股定理易得 ,则由等面积法可得: ,因为D为AB的中点,所以D到平面SBC的距离为: 。
故答案为:C.
【分析】在三角形 中,过A作AE⊥SB交SB于E,再利用线面垂直的定义推出线线垂直,再结合线线垂直证出线面垂直,在三角形SAB中,由勾股定理易得 的长 ,则由等面积法可得 的长,再利用D为AB的中点,从而求出D到平面SBC的距离。
7.【答案】 B
【解析】直线 与平面 ,平面 所成角均为 ,与 所成角为 ,而 , ,又 ,可知: ,
若令二面角 为 ,作 于 , 于 ;过 作 ,过 作 与 交于 点;
∴ 面 ,又 , ,故面 ,面 ,即 ;
过 作 ,过 作 与 交于 点;
∴ 面 ,又 , ,故面 ,面 ,即 ;
作 于 , 于 ,连接 、 ,
即有 ,且 ;
∵ ,即 ,作 有四边形 为正方形,即 ,
∴ ,有 ,故 为等腰三角形且 ,
令 , ,则 ,有 ,而 ,
∴ , ,又 ,
∴ 当 时等号成立
故答案为:B
【分析】由题意知 ,作辅助线找到 , 及二面角 ,四边形 为正方形进而得到 为等腰三角形,利用所得直角三角形用边表示 、 ,即有它们的等量关系,利用 结合二面角 ,即可求 的最大值;
8.【答案】 D
【解析】当 时,
作 于 ,连结 ,
因为 平面 ,
所以 是二面角D-AP-B的平面角,
可以求得 , ,所以 ,
所以排除A、B;
当 时,
作 于 ,连结 ,
因为 平面 ,
所以 是二面角D-AP-B的平面角,
可以求得 , ,
,排除C,
故答案为:D.
【分析】分别取 和 ,计算出二面角D-AP-B的余弦值为 和 ,对比图象得到结果.
9.【答案】 C
【解析】因为直线l与平面 所成的角是 ,直线l在 内的射影与 内的直线m所成角为 ,
所以由最小张角定理可得, , ,
求直线l与直线m所成的角,即是求角 ,且 ,
由题意, ,所以 ,
因此 ,即直线l与直线m所成的角是 ,
故答案为:C.
【分析】利用线面角的求解方法结合射影的定义,从而结合已知条件求出直线l在 内的射影与 内的直线m所成角为 ,再利用最小张角定理可得, , ,求直线l与直线m所成的角,即是求角 ,且 , 由题意, ,所以 ,从而求出的值,进而求出直线l与直线m所成的角。
10.【答案】 A
【解析】解:考虑相对运动,让四面体 保持静止,平面 绕着 旋转, 其垂线也绕着 旋转,如右图,取 中点 ,连结 ,则 ,等价于平面 绕着 旋转,设正四面体 中棱长为2,在 中, , , ,
如下图示,
将问题抽象为如下几何模型,平面 的垂线可视为圆锥的底面半径 ,绕着圆锥的轴 旋转,显然 ,则 ,设 与平面 所成的角为 ,则可得 .
故答案为:A
【分析】考虑相对运动,让四面体 保持静止,平面 绕着 旋转,其垂线也绕着 旋转,取 中点 ,连结 ,则 ,等价于平面 绕着 旋转,推导出 ,将问题抽象为几何模型,平面 的垂线可视为圆锥的底面半径 ,绕着圆锥的轴 旋转,则 ,由此能求出结果.
二、填空题
11.【答案】 4
【解析】 , =(1,2,-1), =(2,1,a),
,解得 .
故答案为:4
【分析】利用向量垂直的性质直接求解即可。
12.【答案】
【解析】平面 的一个法向量为 , ,
所以 ,
∵ ,
∴ 。
故答案为: 。
【分析】 在空间直角坐标系 中,已知 , , 再利用向量的坐标表示求出向量的坐标,再结合空间向量的方法结合数量积求向量夹角公式,从而求出向量 与平面 的法向量的夹角的余弦值,再利用向量 与平面 的法向量的夹角的取值范围,进而结合同角三角函数基本关系式,从而求出向量 与平面 的法向量的夹角的正弦值。
13.【答案】
【解析】因为 面 , ,所以 面 , , ,所以 ,又 ,所以 为 的二面角平面角,所以 .
故答案为: .
【分析】分析翻折前后的变量与不变量,利用面面垂直的性质定理可得 ,求得 ,再利用二面角平面角的定义结合题中已知条件判断 为 的二面角平面角,最后在直角三角形BCD中由 即可求出答案.
14.【答案】 ①②
【解析】过 作 ,垂足为 ;
过 作 ,交 于M;
连接 ,交 于 ,如下图所示:
平面 , 平面 , ,
又 , 平面 , ,
平面 ,
, 平面 ,
平面 , ,
即为 ;
四边形 为正方形, ,
平面 , 平面 , ,
又 平面 , , 平面 ,
, 即为 .
以 为坐标原点,可建立如下图所示的空间直角坐标系,
设 ,
则 , , , , ,
对于①, ,
, ,
,①正确;
对于②, 平面 ,
平面 的一个法向量 ,
又 ,令 ,即 ,
解得: , 存在点 ,使得 平面 ,②正确;
对于③, , ,
令 ,方程无解,
不存在点 ,使得 ,③错误.
故答案为:①②.
【分析】建立空间直角坐标系,求出各个点的坐标,利用向量法验证各个结论,即可得到结果.
15.【答案】
【解析】过点 作 ,垂足为 ,延长 ,使得 (如图),
由题意可得 ,则 ,
由题意知 ,
所以 ,
所以 .
因为 平面 , 平面 ,
所以 又 , , 平面
所以 平面
则 是直线 与平面 所成角的平面角,
,
所以 。
故答案为: 。
【分析】利用 《九章算术》中的“邪田”意为直角梯形,上、下底称为畔,高称为正广,非高腰边称为邪,再利用已知条件结合线面角的求解方法,进而求出邪所在直线与平面 所成角的大小。
16.【答案】
【解析】由题意知, 是正三角形, 是矩形,
设 的中心为 ,矩形 的中心为 ,过 作垂直于平面 的直线 ,过 作垂直于平面 的直线 ,
由球的性质可知,直线 与 的交点 为几何体 的外接球的球心.取 的中点F,连接 ,易得 , , ,
连接 ,显然 与 全等,从而 , ,连接 ,则 为所求几何体外接球的半径,又 ,则 ,故所得几何体外接球的表面积为 .
故答案为: .
【分析】作出图形,取 的外心 ,矩形 的外心 ,分别过 、 作平面 和 的垂线,两垂线的交点即为几何体的外接球的球心,然后求出半径即可求出答案.
17.【答案】 2;
【解析】 , 点 , 在以 为弦长的圆上,
其中 为圆心,则 ,如图:
不妨设 ,当直线 过圆心 时,
最大,此时 , ,
的最大值为2,
而此时, 为等腰三角形, ,
此时,过点 作 ,
,
平面 ,
是二面角 的平面角,
斜线 与平面 成15°角,即
在 中, ,
,
如图:
, ,
在 中, ,可求得 ,
在 中, ,
故答案为:2; 。
【分析】 , 点 , 在以 为弦长的圆上,
其中 为圆心,则 ,不妨设 ,当直线 过圆心 时,
最大,此时 , ,从而求出 的最大值;而此时, 为等腰三角形, ,此时,过点 作 , ,再利用线线垂直证出线面垂直,
平面 再利用线面垂直的定义推出线线垂直,即 , 是二面角 的平面角,再利用已知条件结合直角三角形中的正弦函数定义,从而求出此时二面角 平面角的正弦值 。
18.【答案】
【解析】作 交 于 ,
由于 , ,所以 为正三棱锥,由对称性知 .取 中点 ,连接 ,作 平面 ,交平面 于 ,连接 .作 平面 ,交平面 于 ,连接 .作 ,交 于 ,连接 ,所以 .由于 ,所以 .由于 平面 ,所以 .由于 , 平面 ,所以 .
.因为 , 在 上, 平面 于 , 平面 于 ,所以 .所以 .所以 .由于 都是锐角,所以 .
由于 在 上,由对称性 ,而 ,则 ,由于 也是锐角,所以 .
综上所述,三个角中的最小角是 .
故答案为: .
【分析】作出线线角 ,线面角 ,二面角 ,根据它们的正弦值,比较出它们的大小关系.
三、解答题
19.【答案】 (1)证明:取 的中点 ,连接 、 .
∵点 为 的中点,∴ ,且 ,
又 , ,
∴ ,且 ,
∴四形边 为平行四边形,则 .
而 平面 , 平面
∴ 平面 .
故向量 、 、 共面
(2)解:∵ ,∴ ,
而 , ,
∴ 平面 ,∴ .
又平面 平面 ,平面 平面 ,
∴ 平面 .
如图,以 为坐标原点,分别以 、 、 为 、 、 轴的正方向建立空间直角坐标系
则 , , , .
设平面 的一个法向量为 ,
则 ,即 ,
不妨令 ,可得: .
设平面 的一个法向量为 ,同理可求得 ,
∴ .
∵二面角 为钝二面角,
∴二面角 的余弦值为
【解析】【分析】(1)由已知条件结合中点的性质,即可得出线线平行由此得到 四形边 为平行四边形 ,再由线面平行的判定定理即可得证出结论。
(2)利用线面垂直的性质定理以及判定定理即可得出线面垂直,即可得出线线垂直由此建立空间直角坐标系,求出点以及向量的坐标并设出平面的法向量,结合数量积的坐标公式计算出法向量的坐标,再由向量夹角的公式代入计算出夹角的余弦值,由此得出二面角 的余弦值即可。
20.【答案】 (1)证明:∵PA⊥面ABCD,EF 面ABCD,∴EF⊥AP,在△ABC中,AB=AC, ,
在平行四边形 中,得∠ABC=∠ACB=45°,∴AB⊥AC,且 , 分别为 , 的中点,
∴四边形ABEF为平行四边形,∴AB∥EF,∴AC⊥EF,
∵AP∩AC=C,AP 面PAC,AC 面PAC,∴EF⊥面PAC
(2)解:连接AE,AM,△ABC中,∵AB=AC,E为BC的中点,∴AE⊥BC,平行四边形ABCD中,AD∥BC,∴AE⊥AD,
∵PA⊥平面ABCD,AE 平面ABCD,∴AE⊥PA,∵PA∩AD=A,∴AE⊥平面PAD,
∴AM是EM在平面PAD中的射影,∴∠EMA是EM与平面PAD所成的角,
等腰直角三角形ABC,AB=AC=2,∴BC= AB=2 ,∴AD=2 , ,
∵PA⊥平面ABCD,∴PA⊥AD,∵PA=4,∴PD= ,
又M为PD的中点,故 ,在Rt△MAE中,tan∠EMA= = ,
∴直线ME与平面PAD所成角的正切值为 ,所以直线 与平面 所成的角
【解析】【分析】(1)由题意得EF⊥AP,AB⊥AC, , 分别为 , 的中点,从而四边形ABEF为平行四边形,AB∥EF,进而AC⊥EF,由此能证明EF⊥面PAC.(2)连接AE,AM,推导出AE⊥BC,AE⊥AD,AE⊥PA,从而AE⊥平面PAD,进而∠EMA是EM与平面PAD所成的角,由此能求出直线ME与平面PAD所成角.
21.【答案】 (1)在矩形 中,连接 交 于点 ,则 为 的中点,连接 .
为 的中点
又 平面 , 平面
平面
(2)方法一:
, 平面 , 平面
平面
到平面 的距离等于 到平面 的距离
平面 , 平面
,又 ,
平面
又 平面
平面 平面
过 作 ,则 平面 即为所求.
在 中, , ,解得 .
方法二:(等体积法)
设 到平面 的距离为
平面 , 平面
,又 ,
平面
又
.
【解析】【分析】 (1 )连接AC交BD于点O,则O为AC的中点,连接MO,由OM// PA,即可证明PA//平面MBD;
(2) 方法一: 可得D到平面P BC的距离等于A到平面PBC的距离,过A作AH⊥PB,则AH⊥平面PBC,AH即为所求;
方法二: 设 到平面 的距离为 ,根据等体积法即可求出。
22.【答案】 (1)依据题意,以点 为原点建立空间直角坐标系(如图),
可得 .
由 为棱 的中点,得 .
证明:向量 ,
故 .所以
(2)向量 .
设 为平面 的法向量,
则 即
不妨令 ,可得 为平面 的一个法向量.
于是有 .
所以直线 与平面 所成角的正弦值为 .
(3)向量 .
由点 在棱 上,设 .
故 .
由 ,得 ,因此,
,解得 ,
则 .设 为平面 的法向量,
则 即
不妨令 ,可得 为平面 的一个法向量.
取平面 的一个法向量 ,则
.
易知,二面角 是锐角,所以其余弦值为 .
【解析】【分析】(1)利用空间向量的垂直关系即可判断线线垂直;
(2)利用空间向量直接求解线面角;
(3)利用空间向量直接求解二面角的平面角.
第三章 空间向量与立体几何
一、单选题
1.已知 , ,向量 在 方向上的投影是4,则 =( )
A. 8 B. 12 C. -8 D. 2
2.如图,在四面体VABC中,已知VA⊥平面VBC,VA与平面ABC所成的角为45°,D是BC上一动点,设直线VD与平面ABC所成的角为θ,则( )
A. θ≤60° B. θ≥30° C. θ≤45° D. θ≤75°
3.已知向量 , ,则以 , 为邻边的三角形 的面积( )
A. B. C. 2 D. 4
4.如图,在长方体 中,M,N分别是棱BB1 , B1C1的中点,若∠CMN=90°,则异面直线AD1和DM所成角为( )
A. 30° B. 45° C. 60° D. 90°
5.已知 , , 与 的夹角为 , 是与向量 方向相同的单位向量,则 在向量 上的投影向量为( )
A. B. C. D.
6.三棱锥 中, 底面ABC, , ,D为AB的中点, ,则点D到面 的距离等于( )
A. B. C. D.
7.如图所示,平面 平面 ,二面角 ,已知 , ,直线 与平面 ,平面 所成角均为 ,与 所成角为 ,若 ,则 的最大值是( )
A. B. C. D.
8.在矩形ABCD中,AB=2BC=2,点P在CD边上运动(如图甲),现以AP为折痕将 折起,使得点D在平面ABCP内的射影 恰好落在AB边上(如图乙).设 二面角D-AP-B的余弦值为 ,则函数 的图象大致是( )
B.
C. D.
9.设A为平面 上一点,过点A的直线AO在 平面上的射影为AB,AC为 平面内的一条直线,令 , , ,则这三个角存在一个余弦关系: (其中 和 只能是锐角),称为最小张角定理.直线l与平面 所成的角是 ,若直线l在 内的射影与 内的直线m所成角为 ,则直线l与直线m所成的角是( )
A. B. C. D.
10.正四面体 中, 在平面 内,点 是线段 的中点,在该四面体绕 旋转的过程中,直线 与平面 所成角的余弦值不可能是( )
A. B. C. D. 1
二、填空题
11.向量 =(1,2,-1), =(2,1,a),若 ,则a=________.
12.在空间直角坐标系 中,已知 , ,则向量 与平面 的法向量的夹角的正弦值为________.
13.已知矩形 , ,沿 翻折,使面 ⊥面 ,则二面角 的余弦值为________.
14.若点M在平面 外,过点M作面 的垂线,则称垂足N为点M在平面 内的正投影,记为 .如图,在棱长为 的正方体 中,记平面 为 ,平面 为 ,点 是棱 上一动点(与 不重合), , .给出下列三个结论:①线段 长度的取值范围是 ;②存在点 使得 平面 ;③存在点 使得 .其中正确结论的序号是________.
15.《九章算术》中的“邪田”意为直角梯形,上、下底称为畔,高称为正广,非高腰边称为邪.在四棱锥 中,底面 为邪田,两畔 分别为 ,正广 为 , 平面 ,邪所在直线与平面 所成角的大小为 .
16.在平面五边形 中, , , , ,且 .将五边形 沿对角线 折起,使平面 与平面 所成的二面角为 ,则沿对角线 折起后所得几何体的外接球的表面积是________.
17.斜线 与平面 成15°角,斜足为 , 为 在 内的射影, 为 的中点, 是 内过点 的动直线,若 上存在点 , 使 ,则 则的最大值是________,此时二面角 平面角的正弦值是________
18.设三棱锥 的底面是正三角形,侧棱长均相等, 是棱 上的点(不含端点),记直线 与直线 所成的角为 ,直线 与平面 所成的角为 ,二面角 的平面角为 ,则三个角 、 、 中最小的角是________.
三、解答题
19.四棱锥 中, , , ,平面 平面 ,点 为 的中点.
(1)求证:向量 、 、 共面;
(2)若 ,求二面角 的余弦值.
20.如图,在四棱锥 ,底面 是平行四边形, , 底面 , , , , 分别为 , 的中点, 为线段 的中点.
(1)求证: 面 ;
(2)求直线 与平面 所成的角.
21.如图,在四棱锥 中,四边形 为矩形, 平面 , 是 的中点, , .
(1)求证: 平面
(2)求点 到平面 的距离.
22.如图,在四棱锥 中, 底面 , , , , ,点 为棱 的中点.
(1)证明: ;
(2)求直线 与平面 所成角的正弦值;
(3)若 为棱 上一点,满足 ,求二面角 的余弦值.
答案解析部分
一、单选题
1.【答案】 B
【解析】解: 由题意知向量 在 方向上的投影是4,即 ,
则
故答案为:B
【分析】根据向量的投影,结合向量的数量积,直接求解即可.
2.【答案】 C
【解析】如图,作 底面 于点 , 于 ,由几何关系可得, , ,当 固定时, 也固定, 最小时应为 时,此时 与 重合,又因为VA⊥平面VBC,所以 ,所以 平面 ,易知 三点共线,因为VA与平面ABC所成的角为45°,故 , VA⊥平面VBC,所以 ,所以 ,此时 最大, 最大,故 .
故答案为:C
【分析】先分析出线面角取得最大值的条件,再求出线面角的最大值,即可得出答案。
3.【答案】 B
【解析】因为向量 , ,
所以 , ,
,
因此 ,
所以,以 , 为邻边的三角形 的面积为 .
故答案为:B.
【分析】根据向量夹角的坐标表示,向量模的坐标表示,先求出 ,以及向量的模,再得出 ,根据三角形面积公式,即可得出结果.
4.【答案】 D
【解析】以 为坐标原点, 所在直线分别为 轴,建立空间直角坐标系,如图,
设 ,则 , ,
,
因为 ,所以 ,即有 .
因为 ,所以 ,即异面直线 和 所成角为 .
故答案为:D.
【分析】建立空间直角坐标系,结合 ,求出 的坐标,利用向量夹角公式可求.
5.【答案】 A
【解析】 , , 与 的夹角为 ,
则 ,
,
所以,向量 在向量 方向上的投影为 ,
是与向量 方向相同的单位向量,因此, 在向量 上的投影向量为 .
故答案为:A.
【分析】计算出向量 在向量 方向上的投影 的值,进而可得出 在向量 上的投影向量.
6.【答案】 C
【解析】如图,
在三角形 中,过A作AE⊥SB交SB于E,
因为 面 ,所以 ,又 , ,所以 面 ,因为 面 ,所以 ,而AE⊥SB,且 ,所以AE⊥面SBC.
在三角形SAB中,由勾股定理易得 ,则由等面积法可得: ,因为D为AB的中点,所以D到平面SBC的距离为: 。
故答案为:C.
【分析】在三角形 中,过A作AE⊥SB交SB于E,再利用线面垂直的定义推出线线垂直,再结合线线垂直证出线面垂直,在三角形SAB中,由勾股定理易得 的长 ,则由等面积法可得 的长,再利用D为AB的中点,从而求出D到平面SBC的距离。
7.【答案】 B
【解析】直线 与平面 ,平面 所成角均为 ,与 所成角为 ,而 , ,又 ,可知: ,
若令二面角 为 ,作 于 , 于 ;过 作 ,过 作 与 交于 点;
∴ 面 ,又 , ,故面 ,面 ,即 ;
过 作 ,过 作 与 交于 点;
∴ 面 ,又 , ,故面 ,面 ,即 ;
作 于 , 于 ,连接 、 ,
即有 ,且 ;
∵ ,即 ,作 有四边形 为正方形,即 ,
∴ ,有 ,故 为等腰三角形且 ,
令 , ,则 ,有 ,而 ,
∴ , ,又 ,
∴ 当 时等号成立
故答案为:B
【分析】由题意知 ,作辅助线找到 , 及二面角 ,四边形 为正方形进而得到 为等腰三角形,利用所得直角三角形用边表示 、 ,即有它们的等量关系,利用 结合二面角 ,即可求 的最大值;
8.【答案】 D
【解析】当 时,
作 于 ,连结 ,
因为 平面 ,
所以 是二面角D-AP-B的平面角,
可以求得 , ,所以 ,
所以排除A、B;
当 时,
作 于 ,连结 ,
因为 平面 ,
所以 是二面角D-AP-B的平面角,
可以求得 , ,
,排除C,
故答案为:D.
【分析】分别取 和 ,计算出二面角D-AP-B的余弦值为 和 ,对比图象得到结果.
9.【答案】 C
【解析】因为直线l与平面 所成的角是 ,直线l在 内的射影与 内的直线m所成角为 ,
所以由最小张角定理可得, , ,
求直线l与直线m所成的角,即是求角 ,且 ,
由题意, ,所以 ,
因此 ,即直线l与直线m所成的角是 ,
故答案为:C.
【分析】利用线面角的求解方法结合射影的定义,从而结合已知条件求出直线l在 内的射影与 内的直线m所成角为 ,再利用最小张角定理可得, , ,求直线l与直线m所成的角,即是求角 ,且 , 由题意, ,所以 ,从而求出的值,进而求出直线l与直线m所成的角。
10.【答案】 A
【解析】解:考虑相对运动,让四面体 保持静止,平面 绕着 旋转, 其垂线也绕着 旋转,如右图,取 中点 ,连结 ,则 ,等价于平面 绕着 旋转,设正四面体 中棱长为2,在 中, , , ,
如下图示,
将问题抽象为如下几何模型,平面 的垂线可视为圆锥的底面半径 ,绕着圆锥的轴 旋转,显然 ,则 ,设 与平面 所成的角为 ,则可得 .
故答案为:A
【分析】考虑相对运动,让四面体 保持静止,平面 绕着 旋转,其垂线也绕着 旋转,取 中点 ,连结 ,则 ,等价于平面 绕着 旋转,推导出 ,将问题抽象为几何模型,平面 的垂线可视为圆锥的底面半径 ,绕着圆锥的轴 旋转,则 ,由此能求出结果.
二、填空题
11.【答案】 4
【解析】 , =(1,2,-1), =(2,1,a),
,解得 .
故答案为:4
【分析】利用向量垂直的性质直接求解即可。
12.【答案】
【解析】平面 的一个法向量为 , ,
所以 ,
∵ ,
∴ 。
故答案为: 。
【分析】 在空间直角坐标系 中,已知 , , 再利用向量的坐标表示求出向量的坐标,再结合空间向量的方法结合数量积求向量夹角公式,从而求出向量 与平面 的法向量的夹角的余弦值,再利用向量 与平面 的法向量的夹角的取值范围,进而结合同角三角函数基本关系式,从而求出向量 与平面 的法向量的夹角的正弦值。
13.【答案】
【解析】因为 面 , ,所以 面 , , ,所以 ,又 ,所以 为 的二面角平面角,所以 .
故答案为: .
【分析】分析翻折前后的变量与不变量,利用面面垂直的性质定理可得 ,求得 ,再利用二面角平面角的定义结合题中已知条件判断 为 的二面角平面角,最后在直角三角形BCD中由 即可求出答案.
14.【答案】 ①②
【解析】过 作 ,垂足为 ;
过 作 ,交 于M;
连接 ,交 于 ,如下图所示:
平面 , 平面 , ,
又 , 平面 , ,
平面 ,
, 平面 ,
平面 , ,
即为 ;
四边形 为正方形, ,
平面 , 平面 , ,
又 平面 , , 平面 ,
, 即为 .
以 为坐标原点,可建立如下图所示的空间直角坐标系,
设 ,
则 , , , , ,
对于①, ,
, ,
,①正确;
对于②, 平面 ,
平面 的一个法向量 ,
又 ,令 ,即 ,
解得: , 存在点 ,使得 平面 ,②正确;
对于③, , ,
令 ,方程无解,
不存在点 ,使得 ,③错误.
故答案为:①②.
【分析】建立空间直角坐标系,求出各个点的坐标,利用向量法验证各个结论,即可得到结果.
15.【答案】
【解析】过点 作 ,垂足为 ,延长 ,使得 (如图),
由题意可得 ,则 ,
由题意知 ,
所以 ,
所以 .
因为 平面 , 平面 ,
所以 又 , , 平面
所以 平面
则 是直线 与平面 所成角的平面角,
,
所以 。
故答案为: 。
【分析】利用 《九章算术》中的“邪田”意为直角梯形,上、下底称为畔,高称为正广,非高腰边称为邪,再利用已知条件结合线面角的求解方法,进而求出邪所在直线与平面 所成角的大小。
16.【答案】
【解析】由题意知, 是正三角形, 是矩形,
设 的中心为 ,矩形 的中心为 ,过 作垂直于平面 的直线 ,过 作垂直于平面 的直线 ,
由球的性质可知,直线 与 的交点 为几何体 的外接球的球心.取 的中点F,连接 ,易得 , , ,
连接 ,显然 与 全等,从而 , ,连接 ,则 为所求几何体外接球的半径,又 ,则 ,故所得几何体外接球的表面积为 .
故答案为: .
【分析】作出图形,取 的外心 ,矩形 的外心 ,分别过 、 作平面 和 的垂线,两垂线的交点即为几何体的外接球的球心,然后求出半径即可求出答案.
17.【答案】 2;
【解析】 , 点 , 在以 为弦长的圆上,
其中 为圆心,则 ,如图:
不妨设 ,当直线 过圆心 时,
最大,此时 , ,
的最大值为2,
而此时, 为等腰三角形, ,
此时,过点 作 ,
,
平面 ,
是二面角 的平面角,
斜线 与平面 成15°角,即
在 中, ,
,
如图:
, ,
在 中, ,可求得 ,
在 中, ,
故答案为:2; 。
【分析】 , 点 , 在以 为弦长的圆上,
其中 为圆心,则 ,不妨设 ,当直线 过圆心 时,
最大,此时 , ,从而求出 的最大值;而此时, 为等腰三角形, ,此时,过点 作 , ,再利用线线垂直证出线面垂直,
平面 再利用线面垂直的定义推出线线垂直,即 , 是二面角 的平面角,再利用已知条件结合直角三角形中的正弦函数定义,从而求出此时二面角 平面角的正弦值 。
18.【答案】
【解析】作 交 于 ,
由于 , ,所以 为正三棱锥,由对称性知 .取 中点 ,连接 ,作 平面 ,交平面 于 ,连接 .作 平面 ,交平面 于 ,连接 .作 ,交 于 ,连接 ,所以 .由于 ,所以 .由于 平面 ,所以 .由于 , 平面 ,所以 .
.因为 , 在 上, 平面 于 , 平面 于 ,所以 .所以 .所以 .由于 都是锐角,所以 .
由于 在 上,由对称性 ,而 ,则 ,由于 也是锐角,所以 .
综上所述,三个角中的最小角是 .
故答案为: .
【分析】作出线线角 ,线面角 ,二面角 ,根据它们的正弦值,比较出它们的大小关系.
三、解答题
19.【答案】 (1)证明:取 的中点 ,连接 、 .
∵点 为 的中点,∴ ,且 ,
又 , ,
∴ ,且 ,
∴四形边 为平行四边形,则 .
而 平面 , 平面
∴ 平面 .
故向量 、 、 共面
(2)解:∵ ,∴ ,
而 , ,
∴ 平面 ,∴ .
又平面 平面 ,平面 平面 ,
∴ 平面 .
如图,以 为坐标原点,分别以 、 、 为 、 、 轴的正方向建立空间直角坐标系
则 , , , .
设平面 的一个法向量为 ,
则 ,即 ,
不妨令 ,可得: .
设平面 的一个法向量为 ,同理可求得 ,
∴ .
∵二面角 为钝二面角,
∴二面角 的余弦值为
【解析】【分析】(1)由已知条件结合中点的性质,即可得出线线平行由此得到 四形边 为平行四边形 ,再由线面平行的判定定理即可得证出结论。
(2)利用线面垂直的性质定理以及判定定理即可得出线面垂直,即可得出线线垂直由此建立空间直角坐标系,求出点以及向量的坐标并设出平面的法向量,结合数量积的坐标公式计算出法向量的坐标,再由向量夹角的公式代入计算出夹角的余弦值,由此得出二面角 的余弦值即可。
20.【答案】 (1)证明:∵PA⊥面ABCD,EF 面ABCD,∴EF⊥AP,在△ABC中,AB=AC, ,
在平行四边形 中,得∠ABC=∠ACB=45°,∴AB⊥AC,且 , 分别为 , 的中点,
∴四边形ABEF为平行四边形,∴AB∥EF,∴AC⊥EF,
∵AP∩AC=C,AP 面PAC,AC 面PAC,∴EF⊥面PAC
(2)解:连接AE,AM,△ABC中,∵AB=AC,E为BC的中点,∴AE⊥BC,平行四边形ABCD中,AD∥BC,∴AE⊥AD,
∵PA⊥平面ABCD,AE 平面ABCD,∴AE⊥PA,∵PA∩AD=A,∴AE⊥平面PAD,
∴AM是EM在平面PAD中的射影,∴∠EMA是EM与平面PAD所成的角,
等腰直角三角形ABC,AB=AC=2,∴BC= AB=2 ,∴AD=2 , ,
∵PA⊥平面ABCD,∴PA⊥AD,∵PA=4,∴PD= ,
又M为PD的中点,故 ,在Rt△MAE中,tan∠EMA= = ,
∴直线ME与平面PAD所成角的正切值为 ,所以直线 与平面 所成的角
【解析】【分析】(1)由题意得EF⊥AP,AB⊥AC, , 分别为 , 的中点,从而四边形ABEF为平行四边形,AB∥EF,进而AC⊥EF,由此能证明EF⊥面PAC.(2)连接AE,AM,推导出AE⊥BC,AE⊥AD,AE⊥PA,从而AE⊥平面PAD,进而∠EMA是EM与平面PAD所成的角,由此能求出直线ME与平面PAD所成角.
21.【答案】 (1)在矩形 中,连接 交 于点 ,则 为 的中点,连接 .
为 的中点
又 平面 , 平面
平面
(2)方法一:
, 平面 , 平面
平面
到平面 的距离等于 到平面 的距离
平面 , 平面
,又 ,
平面
又 平面
平面 平面
过 作 ,则 平面 即为所求.
在 中, , ,解得 .
方法二:(等体积法)
设 到平面 的距离为
平面 , 平面
,又 ,
平面
又
.
【解析】【分析】 (1 )连接AC交BD于点O,则O为AC的中点,连接MO,由OM// PA,即可证明PA//平面MBD;
(2) 方法一: 可得D到平面P BC的距离等于A到平面PBC的距离,过A作AH⊥PB,则AH⊥平面PBC,AH即为所求;
方法二: 设 到平面 的距离为 ,根据等体积法即可求出。
22.【答案】 (1)依据题意,以点 为原点建立空间直角坐标系(如图),
可得 .
由 为棱 的中点,得 .
证明:向量 ,
故 .所以
(2)向量 .
设 为平面 的法向量,
则 即
不妨令 ,可得 为平面 的一个法向量.
于是有 .
所以直线 与平面 所成角的正弦值为 .
(3)向量 .
由点 在棱 上,设 .
故 .
由 ,得 ,因此,
,解得 ,
则 .设 为平面 的法向量,
则 即
不妨令 ,可得 为平面 的一个法向量.
取平面 的一个法向量 ,则
.
易知,二面角 是锐角,所以其余弦值为 .
【解析】【分析】(1)利用空间向量的垂直关系即可判断线线垂直;
(2)利用空间向量直接求解线面角;
(3)利用空间向量直接求解二面角的平面角.
