人教新课标A版选修2-2 第二章 推理与证明 单元练习(Word含答案解析)
文档属性
| 名称 | 人教新课标A版选修2-2 第二章 推理与证明 单元练习(Word含答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 145.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览




文档简介
人教新课标A版选修2-2
第二章 推理与证明
一、单选题
1.(2020高二下·宣城期末)学校艺术节对同一类的甲、乙、丙、丁四件参赛作品,只评一个一等奖,在评奖揭晓前, 、 、 、 四位同学对这四件参赛作品预测如下:
说:“乙或丁作品获得一等奖”; 说:“丙作品获得一等奖”; 说:“甲、丁两件作品未获得一等奖”; 说:“乙作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品为( )
A. 甲作品 B. 乙作品 C. 丙作品 D. 丁作品
2.(2020高二下·吉林期末)甲、乙、丙三个学生中有一人申请了去新疆支教,当他们被问到谁申请了去新疆支教时,乙说:甲没有申请;丙说:乙申请了;甲说:乙说对了.如果这三人中有两人说的是真话,一人说了假话,那么申请去新疆支教的学生是( )
A. 甲 B. 乙 C. 丙 D. 不确定
3.(2021·镇江模拟)甲,乙,丙,丁四人参加完某项比赛,当问到四人谁得第一时,回答如下:甲:“我得第一名”;乙:“丁没得第一名”;丙:“乙没得第一名”;丁:“我得第一名”.已知他们四人中只有一个说真话,且只有一人得第一.根据以上信息可以判断得第一名的人是
A. 甲 B. 乙 C. 丙 D. 丁
4.(2020·新高考Ⅰ)基本再生数R0与世代间隔T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型: 描述累计感染病例数I(t)随时间t(单位:天)的变化规律,指数增长率r与R0 , T近似满足R0 =1+rT.有学者基于已有数据估计出R0=3.28,T=6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间约为(ln2≈0.69) ( )
A. 1.2天 B. 1.8天 C. 2.5天 D. 3.5天
5.(2021高二下·宾县月考)用数学归纳法明: 当 时,等式左边应在 的基础上加上( )
A. B. C. D.
6.(2019高二下·来宾期末)如图,有一种游戏画板,要求参与者用六种颜色给画板涂色,这六种颜色分别为红色、黄色1、黄色2、黄色3、金色1、金色2,其中黄色1、黄色2、黄色3是三种不同的颜色,金色1、金色2是两种不同的颜色,要求红色不在两端,黄色1、黄色2、黄色3有且仅有两种相邻,则不同的涂色方案有( )
A. 120种 B. 240种 C. 144种 D. 288种
7.(2021高二下·河南月考)在等差数列 中,若 ,则有等式 ( 且 )成立,类比上述性质,在等比数列 中,若 ,则有( )
A. ( 且 )
B. ( 且 )
C. ( 且 )
D. ( 且 )
8.(2019高二下·珠海期中)如图所示,面积为 的平面凸四边形的第 条边的边长记为 ,此四边形内任一点 到第 条边的距离记为 ,若 ,则 .类比以上性质,体积为 的三棱锥的第 个面的面积记为 ,此三棱锥内任一点 到第 个面的距离记为 ,若 ,则 等于( )
A. B. C. D.
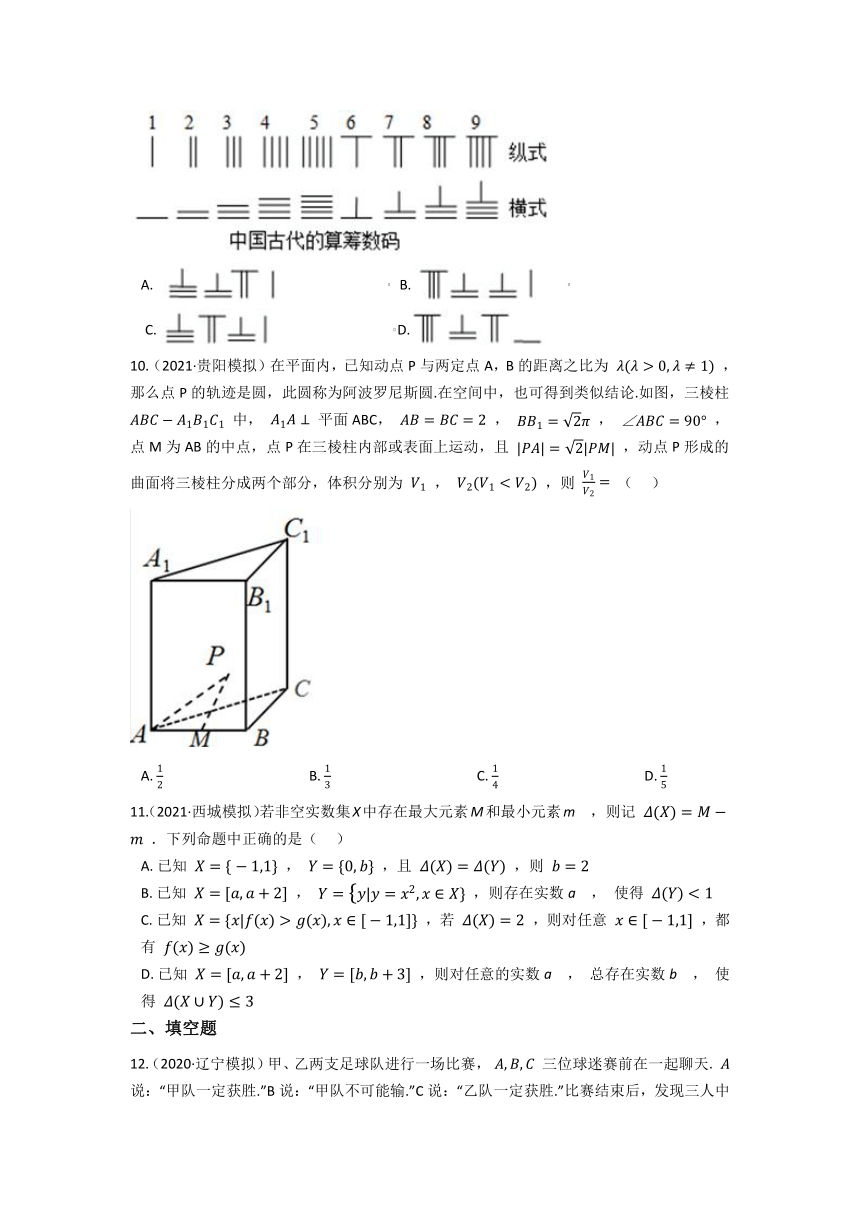
9.(2019高二下·宁夏月考)中国有个名句“运筹帷幄之中,决胜千里之外”,其中的“筹”原意是指《孙子算经》中记载的算筹.古代用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行计算,算筹的摆放形式有横纵两种形式(如图所示),表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位、百位、万位数用纵式表示,十位、千位、十万位用横式表示,以此类推.例如4266用算筹表示就是 ,则8771用算筹可表示为( )
B.
C. D.
10.(2021·贵阳模拟)在平面内,已知动点P与两定点A,B的距离之比为 ,那么点P的轨迹是圆,此圆称为阿波罗尼斯圆.在空间中,也可得到类似结论.如图,三棱柱 中, 平面ABC, , , ,点M为AB的中点,点P在三棱柱内部或表面上运动,且 ,动点P形成的曲面将三棱柱分成两个部分,体积分别为 , ,则 ( )
A. B. C. D.
11.(2021·西城模拟)若非空实数集X中存在最大元素M和最小元素m , 则记 .下列命题中正确的是( )
A. 已知 , ,且 ,则
B. 已知 , ,则存在实数a , 使得
C. 已知 ,若 ,则对任意 ,都有
D. 已知 , ,则对任意的实数a , 总存在实数b , 使得
二、填空题
12.(2020·辽宁模拟)甲、乙两支足球队进行一场比赛, 三位球迷赛前在一起聊天. 说:“甲队一定获胜.”B说:“甲队不可能输.”C说:“乙队一定获胜.”比赛结束后,发现三人中只有一人的判断是正确的,则比赛的结果不可能是________.(填“甲胜”“乙胜”“平局”中的一个)
13.(2019·齐齐哈尔模拟)甲、乙、丙三个同学同时做标号为 、 、 的三个题,甲做对了两个题,乙做对了两个题,丙做对了两个题,则下列说法正确的是________(填所有正确说法的编号).
①三个题都有人做对;②至少有一个题三个人都做对;③至少有两个题有两个人都做对.
14.(2021·葫芦岛模拟)迎春杯数学竞赛后,甲 乙 丙 丁四名同学猜测他们之中谁能获奖.甲说:“如果我能获奖,那么乙也能获奖.”乙说:“如果我能获奖,那么丙也能获奖.”丙说:“如果丁没获奖,那么我也不能获奖.”实际上,他们之中只有一个人没有获奖,并且甲 乙 丙说的话都是正确的.那么没能获奖的同学是 .
15.(2019·奉贤模拟)天干地支纪年法,源于中国,中国自古便有十天干与十二地支.十天干:甲、乙、丙、丁、戊、己、庚、辛、壬、癸.十二地支:子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.天干地支纪年法是按顺序以一个天干和一个地支相配,排列起来,天干在前,地支在后,天干由“甲”起,地支由“子”起,比如第一年为“甲子”,第二年为“乙丑”,第三年为“丙寅”,…,以此类推,排列到“癸酉”后,天干回到“甲”重新开始,即“甲戌”,“乙亥”,之后地支回到“子”重新开始,即“丙子”,…,以此类推,已知2016年为丙申年,那么到改革开放100年时,即2078年为________年
16.(2020高二下·河南月考)甲、乙、丙三位同学被问到是否去过A,B,C三个城市时,
甲说:我去过的城市比乙多,但没去过B城市;
乙说:我没去过C城市.
丙说:我们三个去过同一城市.
由此可判断乙去过的城市为________
17.(2019高三上·广东月考)在我国南宋数学家杨辉所著的《详解九章算法》(1261年)一书中,用如图 所示的三角形,解释二项和的乘方规律.在欧洲直到1623年以后,法国数学家布莱士 帕斯卡的著作(1655年)介绍了这个三角形,近年来,国外也逐渐承认这项成果属于中国,所以有些书上称这是“中国三角形” ,如图 .17世纪德国数学家莱布尼茨发现了“莱布尼茨三角形”,如图 .在杨辉三角中,相邻两行满足关系式: ,其 中 是行数, .请类比上式,在莱布尼茨三角形中相邻两行满足的关系式是________.
18.(2019高二下·宁夏月考)已知 的周长为 ,面积为 ,则 的内切圆半径为 .将此结论类比到空间,已知四面体 的表面积为 ,体积为 ,则四面体 的内切球的半径 ________.
19.(2021高二上·砀山月考)如图,正方体 的棱长为2,E , F分别为 , 的中点,则以下说法错误的是 (写序号)
①N为 上一点,则平面 与平面 所成二面角的大小与点N位置无关
② 存在上一点P , 使得 平面
③ 三棱锥 和 体积相等
④ 上存在一点M , 使得
20.(2019高一上·上海月考)已知有限集 . 如果A中元素 满足 ,就称A为“复活集”,给出下列结论:
①集合 是“复活集”;
②若 ,且 是“复活集”,则 ;
③若 ,则 不可能是“复活集”;
④若 ,则“复活集”A有且只有一个,且 .
其中正确的结论是________.(填上你认为所有正确的结论序号)
三、解答题
21.(2020高二上·保定期末)已知函数 .
(1) 恒成立,求a的取值范围;
(2)当 时,求 在区间 的最小值;
(3)证明:当 时, .
22.(2019高二下·上海期中)平面图形很多可以推广到空间中去,例如正三角形可以推广到正四面体,圆可以推广到球,平行四边形可以推广到平行六面体,直角三角形也可以推广到直角四面体,如果四面体 中棱 两两垂直,那么称四面体 为直角四面体. 请类比直角三角形中的性质给出2个直角四面体中的性质,并给出证明.(请在结论 中选择1个,结论4,5中选择1个,写出它们在直角四面体中的类似结论,并给出证明,多选不得分,其中 表示斜边上的高, 分别表示内切圆与外接圆的半径)
直角三角形 直角四面体
条件
结论1
结论2
结论3
结论4
结论5
答案解析部分
一、单选题
1.【答案】 C
【解析】若甲作品为一等奖,则 、 、 、 的说法均错误,故不满足题意;
若乙作品为一等奖,则 、 、 的说法正确, 的说法错误,故不满足题意;
若丙作品为一等奖,则 、 的说法均正确, 、 的说法均错误,故满足题意;
若丁作品为一等奖,则 的说法正确, 、 、 的说法均错误,故不满足题意;
若这四位同学中只有两位说的话是对的,则获得等奖的作品是丙作品,
故答案为:C.
【分析】 根据题意由简单的合情推理即可得出若丙作品为等奖,则B、C的说法均正确,A、D的说法均错误,故丙获得一等奖满足题意.
2.【答案】 C
【解析】若乙说了假话,则甲、丙说了真话,那么甲、乙都申请了,与题意只有一人申请矛盾;
若丙说了假话,则甲、乙说的话为真,甲、乙都没有申请,申请的人是丙,满足题意,
故答案为:C.
【分析】利用已知条件结合演绎推理的方法,进而找出申请去新疆支教的学生。
3.【答案】 B
【解析】解:若甲得第一名,则甲、乙、丙说了真话,丁说了假话,不符合题意;
若乙得第一名,则乙说了真话,甲、丙、丁说了假话,符合题意;
若丙得第一名,则乙、丙说了真话,甲、丁说了假话,不符合题意;
若丁得第一名,则丙、丁说了真话,甲、乙说了假话,不符合题意
故答案为:B
【分析】 分别假设第一名是甲、乙、丙、丁,分析四个人说的话,由此能求出结果.
4.【答案】 B
【解析】因为 , , ,所以 ,所以 ,
设在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间为 天,
则 ,所以 ,所以 ,
所以 天.
故答案为:B.
【分析】根据题意可得 ,设在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间为 天,根据 ,解得 即可得结果.
5.【答案】 C
【解析】用数学归纳法证明:
当 时,则
当 ,左式= ,
当 时,等式左边应在 的基础上应该加上 。
故答案为:C
【分析】利用已知条件结合数学归纳法证明步骤,从而得出等式左边应在 的基础上应该加上 。
6.【答案】 D
【解析】不考虑红色的位置,黄色1、黄色2、黄色3有且仅有两个相邻的涂色方案有 种. 这种情况下,红色在左右两端的涂色方案有 种;从而所求的结果为 种.
故答案为:D.
【分析】首先计算出“黄色1、黄色2、黄色3有且仅有两个相邻的涂色方案”数,然后计算出“红色在左右两端,黄色1、黄色2、黄色3有且仅有两个相邻的涂色方案”数,用前者减去后者,求得题目所求不同的涂色方案总数.
7.【答案】 A
【解析】在等差数列 中,有
所以有
在等比数列 中,若 ,则
当 时,则 ,
则
当 时,则 ,
则
所以
故答案为:A
【分析】利用已知条件结合类比推理的方法,进而选出正确的答案。
8.【答案】 D
【解析】解:面积为 的平面凸四边形的第 条边的边长记为 ,
此四边形内任一点 到第 条边的距离记为 ,
所以由等面积法得, ,
因为 ,
,
所以 ,
即 ,
故在平面凸四边形中,求解此结论的过程中运用了等面积法求解,
类比上述性质,在三棱锥中,则应使用等体积法求解,
三棱锥的体积为 ,
因为体积为 的三棱锥的第 个面的面积记为 ,此三棱锥内任一点 到第 个面的距离记为 ,
由等体积法有, ,
,
因为 ,
所以 ,
所以 ,
即 ,
故选D.
【分析】平面凸四边形中的结论是根据等面积法得到,类比以上性质,在三棱锥中根据等体积法求解 的值.
9.【答案】 C
【解析】解:由算筹含义得到8771用算筹可表示为 .
故答案为:C.
【分析】由算筹含义直接求解.
10.【答案】 D
【解析】如图,在平面PAB中,作 ,交AB于点N,则 ,
又因 ,所以 ,
所以 ,所以 ,
所以 .
因为 ,所以 ,
所以B、N重合且 ,
所以点P落在以B为球心, 为半径的球面上.
作 于H,则 ,
因为 面ABC,所以 BH,
又因为 ,所以 面 ,
所以B到面 的距离为 ,
所以球面与面 相切,而 ,
所以球面不会与面 相交,
则 ,
,
所以 ,
所以 。
故答案为:D.
【分析】在平面PAB中,作 ,交AB于点N,则 ,又因 ,再利用两三角形相似的判断方法,所以 ,再利用两三角形相似对应边成比例,所以 ,所以 ,所以 , 因为 ,所以 ,所以B、N重合且 ,所以点P落在以B为球心, 为半径的球面上,作 于H,则 ,因为 面ABC,再利用线面垂直的定义证出线线垂直,所以 BH,再利用线线垂直证出线面垂直,所以 面 ,所以B到面 的距离为 ,所以球面与面 相切,而 ,所以球面不会与面 相交,进而求出则的值 ,再利用三棱柱的体积公式求出三棱柱的体积,再利用作差法求出 的值 ,进而求出 。
11.【答案】 D
【解析】对于A:由 ,则 ; ,则 ,解得: ,A不符合题意;
对于B:由 ,则 ;
,则 ,
①当 时, 在 上单减,所以 ,解得: ,又 ,所以a不存在;
②当 时, 在 上单减,在 上单增,且 所以 ,解得: ,又 ,所以a不存在;
③当 时, 在 上单减,在 上单增,且 所以 ,解得: ,又 ,所以a不存在;
④当 时, 在 上单增,所以 ,解得: ,又 ,所以a不存在;
综上所述:不存在实数a , 使得 .
B不符合题意;
对于C:∵ ,而 ,则M=1,N=-1,但对任意 ,都有 ,不一定成立;
对于D:∵ ,∴ ,由 得 ,所以则对任意的实数a , 总存在实数b , 使得 ,D成立.
故答案为:D
【分析】根据题意对选项 A举反例判断;选项B用反证法,分类讨论判断;选项C举反例判断; 选项D对任意的实数a,求出b满足条件即可.
二、填空题
12.【答案】 甲胜
【解析】若甲队获胜,则A,B判断都正确,与三人中只有一人的判断是正确的矛盾,故甲不可能获胜.
故答案为:甲胜
【分析】分析若甲队获胜,可得出矛盾,即得解.
13.【答案】 ③
【解析】若甲做对 、 ,乙做对 、 ,丙做对 、 ,则 题无人做对,所以①错误;
若甲做对 、 , 乙做对 、 ,丙做对 、 ,则没有一个题被三个人都做对,所以②错误.
做对的情况可分为这三种:三个人做对的都相同;三个人中有两个人做对的相同;三个人每个人做对的都不完全相同,分类可知三种情况都满足③的说法.
故答案是:③.
【分析】根据题意结合所给的条件进行合理的推理,即可得出结论。
14.【答案】 甲
【解析】首先根据丙说的话可以推知,丁必能获奖,否则,假设丁没有获奖,那么丙也没有获奖,这与“他们之中只有一个人没有获奖”矛盾;
其次考虑甲是否获奖,假设甲能获奖,那么根据甲说的话可以推知,乙也可获奖;再根据乙说的话又可以推知丙也能获奖,这样得出4个人全都能获奖,不可能;
因此,只有甲没有获奖.
故答案为:甲
【分析】根据题意丙说的话进行分析可得丁获奖,进而分析甲的情况假设甲获奖进行推导得矛盾,即可得答案。
15.【答案】 戊戌
【解析】由题意,可得数列天干是以10为公差的等差数列,地支是以12为公差的等差数列,
从2017年到2078年经过了61年,且2017年为丁茜年,以2017年的天干和地支分别为首项,则 余 ,则2078年的天干为戊, 余 ,则2078年的天干为戌,
所以2078年为戊戌年。
【分析】首先根据题意得出数列天干是以10为公差的等差数列,地支是以12为公差的等差数列,以2017年的天干和地支分别为首项,由此得出结果。
16.【答案】 A
【解析】由乙说:我没去过C城市,则乙可能去过A城市或B城市,但甲说:我去过的城市比乙多,但没去过B城市,则乙只能是去过A,B中的任一个,再由丙说:我们三人去过同一城市,则由此可判断乙去过的城市为A
【分析】由已知进行简单的推理,即可判断乙去过的城市为A.
17.【答案】
【解析】解:类比观察得,将莱布尼茨三角形的每一行都能提出倍数 ,
而相邻两项之和是上一行的两者相拱之数,所以类比式子 ,有 .
故答案为: .
【分析】这是一个考查类比推理的题目,解题的关键是仔细观察图中给出的莱布尼茨三角形,并从三解数阵中,找出行与行之间数的关系,探究规律并其表示出来.
18.【答案】
【解析】在平面中,设内切圆的圆心为 ,半径为 ,连结 ,则有
所以 ,类比到空间可得,设内切球的球心为 ,半径为 ,则有
所以四面体 的内切球的半径为 .
【分析】利用已知条件结合类比推理的方法,从而得出四面体 的内切球的半径。
19.【答案】 ②
【解析】解:对于①,因为N为 上一点,所以平面 与平面 所成二面角α即为平面 与平面 BCC1B1所成二面角β,显然β是固定角,故①正确;
对于②,假设BB上存在点P,使得C1P⊥平面EFB1C,则C1P⊥FB1 , 而FB1⊥B1C1 , 所以FB1⊥平面BB1C1C,显然错误,故②错误;
对于③, , 又 ,
所以 , 而 ,
连接DA1 , 则F到平面DB1C的距离即为F到A1D的距离,所以,
所以
所以 , 故③正确;
对于④,以D1为原点,分别以D1A1 , D1D,D1C1为x,y,z轴建立空间直角坐标系,
则C(0,2,2),F(2,0,1),M(x,0,0),
则
当 , 即 , 即时, ,
此时 , 故④正确
故答案为:②
【分析】根据二面角的平面角的定义可判断①,运用反证法结合直线与平面垂直的判定定理可判断②,根据棱锥的体积公式,结合点到平面的距离,运用等体积法可判断③,利用向量法结合向量数量积运算的坐标表示可判断④.
20.【答案】 ①③④
【解析】对于①, ,故①正确;
对于②,不妨设 ,
则由韦达定理知 是一元二次方程 的两个根,
由 ,可得 或 ,故②错;
对于③,不妨设 中 ,
由 得 ,
当 时,即有 ,
,于是 , 无解,即不存在满足条件的“复活集”A,故③正确;
对于④,当 时, ,故只能 , ,求得 ,
于是“复活集” A只有一个,为 ,
当 时,由 ,
即有 ,
也就是说“复活集”A存在的必要条件是 ,
事实上 ,矛盾,
当 时不存在“复活集”A,故④正确.
故答案为:①③④
【分析】根据已知中“复活集”的定义,结合韦达定理以及反证法,依次判断四个结论的正误,进而可得答案.
三、解答题
21.【答案】 (1)解: , 恒成立,即为 ,也就是 在 上恒成立.
令 , , ,
当 时, , 单调递减,当 时, , 单调递增,
在 时, 取到极小值也是最小值, ,
所以
(2)解:当 时, ,
当 时, 时, , 单调递减,当 时, , 单调递增,
∴ 时 取到极小值也是最小值,即 ,
当 时, , , 单调递增,
(3)证明:要证当 时, .即证当 时, .
由(2)知当 时,函数 在 处的最小值为 ,
令 .∴ ,由 得 ,
所以在 得函数,在 为减函数,所以 ,
当 时, .
即当 时,
【解析】【分析】(1) , 恒成立,即为 恒成立,可化为. 在 上恒成立, 令 , , 利用导数研究其单调性极值
与最值即可得出 a的取值范围;
(2) 当 时, , 求导,根据导数的符号可得出 的单调性,进而求得 在区间 的最小值;
(3)要证当 时, , 即证当 时, , 令 , , 由 得 , 在 为减函数,所以 , 进而证得 .
22.【答案】 解:记 的面积依次为 ,
平面 与 所成角依次为 ,
点 到平面 的距离为 分别表示内切球与外接球的半径,内切球的球心为 ,
直角三角形 直角四面体
条件
结论1
结论2
结论3
结论4
结论5
证明:设 ,
过 作 ,垂足为 ,联结 ,过 作 ,垂足为 ,
易证: , 平面 ,则 ,
结论1: ,
在 中, ,
s
;
结论2: ,
∴ 。
同理, ,
∴ ;
结论3:∵ ,∴ ,
又 ,
∴
结论4: ,
∴ .
从而 ,即 ;
结论5:将直角四面体 补形成为以 为长、宽、高的长方体,
则长方体的体对角线即为直角四面体ABCD的外接球的直径,即 .
第二章 推理与证明
一、单选题
1.(2020高二下·宣城期末)学校艺术节对同一类的甲、乙、丙、丁四件参赛作品,只评一个一等奖,在评奖揭晓前, 、 、 、 四位同学对这四件参赛作品预测如下:
说:“乙或丁作品获得一等奖”; 说:“丙作品获得一等奖”; 说:“甲、丁两件作品未获得一等奖”; 说:“乙作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品为( )
A. 甲作品 B. 乙作品 C. 丙作品 D. 丁作品
2.(2020高二下·吉林期末)甲、乙、丙三个学生中有一人申请了去新疆支教,当他们被问到谁申请了去新疆支教时,乙说:甲没有申请;丙说:乙申请了;甲说:乙说对了.如果这三人中有两人说的是真话,一人说了假话,那么申请去新疆支教的学生是( )
A. 甲 B. 乙 C. 丙 D. 不确定
3.(2021·镇江模拟)甲,乙,丙,丁四人参加完某项比赛,当问到四人谁得第一时,回答如下:甲:“我得第一名”;乙:“丁没得第一名”;丙:“乙没得第一名”;丁:“我得第一名”.已知他们四人中只有一个说真话,且只有一人得第一.根据以上信息可以判断得第一名的人是
A. 甲 B. 乙 C. 丙 D. 丁
4.(2020·新高考Ⅰ)基本再生数R0与世代间隔T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型: 描述累计感染病例数I(t)随时间t(单位:天)的变化规律,指数增长率r与R0 , T近似满足R0 =1+rT.有学者基于已有数据估计出R0=3.28,T=6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间约为(ln2≈0.69) ( )
A. 1.2天 B. 1.8天 C. 2.5天 D. 3.5天
5.(2021高二下·宾县月考)用数学归纳法明: 当 时,等式左边应在 的基础上加上( )
A. B. C. D.
6.(2019高二下·来宾期末)如图,有一种游戏画板,要求参与者用六种颜色给画板涂色,这六种颜色分别为红色、黄色1、黄色2、黄色3、金色1、金色2,其中黄色1、黄色2、黄色3是三种不同的颜色,金色1、金色2是两种不同的颜色,要求红色不在两端,黄色1、黄色2、黄色3有且仅有两种相邻,则不同的涂色方案有( )
A. 120种 B. 240种 C. 144种 D. 288种
7.(2021高二下·河南月考)在等差数列 中,若 ,则有等式 ( 且 )成立,类比上述性质,在等比数列 中,若 ,则有( )
A. ( 且 )
B. ( 且 )
C. ( 且 )
D. ( 且 )
8.(2019高二下·珠海期中)如图所示,面积为 的平面凸四边形的第 条边的边长记为 ,此四边形内任一点 到第 条边的距离记为 ,若 ,则 .类比以上性质,体积为 的三棱锥的第 个面的面积记为 ,此三棱锥内任一点 到第 个面的距离记为 ,若 ,则 等于( )
A. B. C. D.
9.(2019高二下·宁夏月考)中国有个名句“运筹帷幄之中,决胜千里之外”,其中的“筹”原意是指《孙子算经》中记载的算筹.古代用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行计算,算筹的摆放形式有横纵两种形式(如图所示),表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位、百位、万位数用纵式表示,十位、千位、十万位用横式表示,以此类推.例如4266用算筹表示就是 ,则8771用算筹可表示为( )
B.
C. D.
10.(2021·贵阳模拟)在平面内,已知动点P与两定点A,B的距离之比为 ,那么点P的轨迹是圆,此圆称为阿波罗尼斯圆.在空间中,也可得到类似结论.如图,三棱柱 中, 平面ABC, , , ,点M为AB的中点,点P在三棱柱内部或表面上运动,且 ,动点P形成的曲面将三棱柱分成两个部分,体积分别为 , ,则 ( )
A. B. C. D.
11.(2021·西城模拟)若非空实数集X中存在最大元素M和最小元素m , 则记 .下列命题中正确的是( )
A. 已知 , ,且 ,则
B. 已知 , ,则存在实数a , 使得
C. 已知 ,若 ,则对任意 ,都有
D. 已知 , ,则对任意的实数a , 总存在实数b , 使得
二、填空题
12.(2020·辽宁模拟)甲、乙两支足球队进行一场比赛, 三位球迷赛前在一起聊天. 说:“甲队一定获胜.”B说:“甲队不可能输.”C说:“乙队一定获胜.”比赛结束后,发现三人中只有一人的判断是正确的,则比赛的结果不可能是________.(填“甲胜”“乙胜”“平局”中的一个)
13.(2019·齐齐哈尔模拟)甲、乙、丙三个同学同时做标号为 、 、 的三个题,甲做对了两个题,乙做对了两个题,丙做对了两个题,则下列说法正确的是________(填所有正确说法的编号).
①三个题都有人做对;②至少有一个题三个人都做对;③至少有两个题有两个人都做对.
14.(2021·葫芦岛模拟)迎春杯数学竞赛后,甲 乙 丙 丁四名同学猜测他们之中谁能获奖.甲说:“如果我能获奖,那么乙也能获奖.”乙说:“如果我能获奖,那么丙也能获奖.”丙说:“如果丁没获奖,那么我也不能获奖.”实际上,他们之中只有一个人没有获奖,并且甲 乙 丙说的话都是正确的.那么没能获奖的同学是 .
15.(2019·奉贤模拟)天干地支纪年法,源于中国,中国自古便有十天干与十二地支.十天干:甲、乙、丙、丁、戊、己、庚、辛、壬、癸.十二地支:子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.天干地支纪年法是按顺序以一个天干和一个地支相配,排列起来,天干在前,地支在后,天干由“甲”起,地支由“子”起,比如第一年为“甲子”,第二年为“乙丑”,第三年为“丙寅”,…,以此类推,排列到“癸酉”后,天干回到“甲”重新开始,即“甲戌”,“乙亥”,之后地支回到“子”重新开始,即“丙子”,…,以此类推,已知2016年为丙申年,那么到改革开放100年时,即2078年为________年
16.(2020高二下·河南月考)甲、乙、丙三位同学被问到是否去过A,B,C三个城市时,
甲说:我去过的城市比乙多,但没去过B城市;
乙说:我没去过C城市.
丙说:我们三个去过同一城市.
由此可判断乙去过的城市为________
17.(2019高三上·广东月考)在我国南宋数学家杨辉所著的《详解九章算法》(1261年)一书中,用如图 所示的三角形,解释二项和的乘方规律.在欧洲直到1623年以后,法国数学家布莱士 帕斯卡的著作(1655年)介绍了这个三角形,近年来,国外也逐渐承认这项成果属于中国,所以有些书上称这是“中国三角形” ,如图 .17世纪德国数学家莱布尼茨发现了“莱布尼茨三角形”,如图 .在杨辉三角中,相邻两行满足关系式: ,其 中 是行数, .请类比上式,在莱布尼茨三角形中相邻两行满足的关系式是________.
18.(2019高二下·宁夏月考)已知 的周长为 ,面积为 ,则 的内切圆半径为 .将此结论类比到空间,已知四面体 的表面积为 ,体积为 ,则四面体 的内切球的半径 ________.
19.(2021高二上·砀山月考)如图,正方体 的棱长为2,E , F分别为 , 的中点,则以下说法错误的是 (写序号)
①N为 上一点,则平面 与平面 所成二面角的大小与点N位置无关
② 存在上一点P , 使得 平面
③ 三棱锥 和 体积相等
④ 上存在一点M , 使得
20.(2019高一上·上海月考)已知有限集 . 如果A中元素 满足 ,就称A为“复活集”,给出下列结论:
①集合 是“复活集”;
②若 ,且 是“复活集”,则 ;
③若 ,则 不可能是“复活集”;
④若 ,则“复活集”A有且只有一个,且 .
其中正确的结论是________.(填上你认为所有正确的结论序号)
三、解答题
21.(2020高二上·保定期末)已知函数 .
(1) 恒成立,求a的取值范围;
(2)当 时,求 在区间 的最小值;
(3)证明:当 时, .
22.(2019高二下·上海期中)平面图形很多可以推广到空间中去,例如正三角形可以推广到正四面体,圆可以推广到球,平行四边形可以推广到平行六面体,直角三角形也可以推广到直角四面体,如果四面体 中棱 两两垂直,那么称四面体 为直角四面体. 请类比直角三角形中的性质给出2个直角四面体中的性质,并给出证明.(请在结论 中选择1个,结论4,5中选择1个,写出它们在直角四面体中的类似结论,并给出证明,多选不得分,其中 表示斜边上的高, 分别表示内切圆与外接圆的半径)
直角三角形 直角四面体
条件
结论1
结论2
结论3
结论4
结论5
答案解析部分
一、单选题
1.【答案】 C
【解析】若甲作品为一等奖,则 、 、 、 的说法均错误,故不满足题意;
若乙作品为一等奖,则 、 、 的说法正确, 的说法错误,故不满足题意;
若丙作品为一等奖,则 、 的说法均正确, 、 的说法均错误,故满足题意;
若丁作品为一等奖,则 的说法正确, 、 、 的说法均错误,故不满足题意;
若这四位同学中只有两位说的话是对的,则获得等奖的作品是丙作品,
故答案为:C.
【分析】 根据题意由简单的合情推理即可得出若丙作品为等奖,则B、C的说法均正确,A、D的说法均错误,故丙获得一等奖满足题意.
2.【答案】 C
【解析】若乙说了假话,则甲、丙说了真话,那么甲、乙都申请了,与题意只有一人申请矛盾;
若丙说了假话,则甲、乙说的话为真,甲、乙都没有申请,申请的人是丙,满足题意,
故答案为:C.
【分析】利用已知条件结合演绎推理的方法,进而找出申请去新疆支教的学生。
3.【答案】 B
【解析】解:若甲得第一名,则甲、乙、丙说了真话,丁说了假话,不符合题意;
若乙得第一名,则乙说了真话,甲、丙、丁说了假话,符合题意;
若丙得第一名,则乙、丙说了真话,甲、丁说了假话,不符合题意;
若丁得第一名,则丙、丁说了真话,甲、乙说了假话,不符合题意
故答案为:B
【分析】 分别假设第一名是甲、乙、丙、丁,分析四个人说的话,由此能求出结果.
4.【答案】 B
【解析】因为 , , ,所以 ,所以 ,
设在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间为 天,
则 ,所以 ,所以 ,
所以 天.
故答案为:B.
【分析】根据题意可得 ,设在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间为 天,根据 ,解得 即可得结果.
5.【答案】 C
【解析】用数学归纳法证明:
当 时,则
当 ,左式= ,
当 时,等式左边应在 的基础上应该加上 。
故答案为:C
【分析】利用已知条件结合数学归纳法证明步骤,从而得出等式左边应在 的基础上应该加上 。
6.【答案】 D
【解析】不考虑红色的位置,黄色1、黄色2、黄色3有且仅有两个相邻的涂色方案有 种. 这种情况下,红色在左右两端的涂色方案有 种;从而所求的结果为 种.
故答案为:D.
【分析】首先计算出“黄色1、黄色2、黄色3有且仅有两个相邻的涂色方案”数,然后计算出“红色在左右两端,黄色1、黄色2、黄色3有且仅有两个相邻的涂色方案”数,用前者减去后者,求得题目所求不同的涂色方案总数.
7.【答案】 A
【解析】在等差数列 中,有
所以有
在等比数列 中,若 ,则
当 时,则 ,
则
当 时,则 ,
则
所以
故答案为:A
【分析】利用已知条件结合类比推理的方法,进而选出正确的答案。
8.【答案】 D
【解析】解:面积为 的平面凸四边形的第 条边的边长记为 ,
此四边形内任一点 到第 条边的距离记为 ,
所以由等面积法得, ,
因为 ,
,
所以 ,
即 ,
故在平面凸四边形中,求解此结论的过程中运用了等面积法求解,
类比上述性质,在三棱锥中,则应使用等体积法求解,
三棱锥的体积为 ,
因为体积为 的三棱锥的第 个面的面积记为 ,此三棱锥内任一点 到第 个面的距离记为 ,
由等体积法有, ,
,
因为 ,
所以 ,
所以 ,
即 ,
故选D.
【分析】平面凸四边形中的结论是根据等面积法得到,类比以上性质,在三棱锥中根据等体积法求解 的值.
9.【答案】 C
【解析】解:由算筹含义得到8771用算筹可表示为 .
故答案为:C.
【分析】由算筹含义直接求解.
10.【答案】 D
【解析】如图,在平面PAB中,作 ,交AB于点N,则 ,
又因 ,所以 ,
所以 ,所以 ,
所以 .
因为 ,所以 ,
所以B、N重合且 ,
所以点P落在以B为球心, 为半径的球面上.
作 于H,则 ,
因为 面ABC,所以 BH,
又因为 ,所以 面 ,
所以B到面 的距离为 ,
所以球面与面 相切,而 ,
所以球面不会与面 相交,
则 ,
,
所以 ,
所以 。
故答案为:D.
【分析】在平面PAB中,作 ,交AB于点N,则 ,又因 ,再利用两三角形相似的判断方法,所以 ,再利用两三角形相似对应边成比例,所以 ,所以 ,所以 , 因为 ,所以 ,所以B、N重合且 ,所以点P落在以B为球心, 为半径的球面上,作 于H,则 ,因为 面ABC,再利用线面垂直的定义证出线线垂直,所以 BH,再利用线线垂直证出线面垂直,所以 面 ,所以B到面 的距离为 ,所以球面与面 相切,而 ,所以球面不会与面 相交,进而求出则的值 ,再利用三棱柱的体积公式求出三棱柱的体积,再利用作差法求出 的值 ,进而求出 。
11.【答案】 D
【解析】对于A:由 ,则 ; ,则 ,解得: ,A不符合题意;
对于B:由 ,则 ;
,则 ,
①当 时, 在 上单减,所以 ,解得: ,又 ,所以a不存在;
②当 时, 在 上单减,在 上单增,且 所以 ,解得: ,又 ,所以a不存在;
③当 时, 在 上单减,在 上单增,且 所以 ,解得: ,又 ,所以a不存在;
④当 时, 在 上单增,所以 ,解得: ,又 ,所以a不存在;
综上所述:不存在实数a , 使得 .
B不符合题意;
对于C:∵ ,而 ,则M=1,N=-1,但对任意 ,都有 ,不一定成立;
对于D:∵ ,∴ ,由 得 ,所以则对任意的实数a , 总存在实数b , 使得 ,D成立.
故答案为:D
【分析】根据题意对选项 A举反例判断;选项B用反证法,分类讨论判断;选项C举反例判断; 选项D对任意的实数a,求出b满足条件即可.
二、填空题
12.【答案】 甲胜
【解析】若甲队获胜,则A,B判断都正确,与三人中只有一人的判断是正确的矛盾,故甲不可能获胜.
故答案为:甲胜
【分析】分析若甲队获胜,可得出矛盾,即得解.
13.【答案】 ③
【解析】若甲做对 、 ,乙做对 、 ,丙做对 、 ,则 题无人做对,所以①错误;
若甲做对 、 , 乙做对 、 ,丙做对 、 ,则没有一个题被三个人都做对,所以②错误.
做对的情况可分为这三种:三个人做对的都相同;三个人中有两个人做对的相同;三个人每个人做对的都不完全相同,分类可知三种情况都满足③的说法.
故答案是:③.
【分析】根据题意结合所给的条件进行合理的推理,即可得出结论。
14.【答案】 甲
【解析】首先根据丙说的话可以推知,丁必能获奖,否则,假设丁没有获奖,那么丙也没有获奖,这与“他们之中只有一个人没有获奖”矛盾;
其次考虑甲是否获奖,假设甲能获奖,那么根据甲说的话可以推知,乙也可获奖;再根据乙说的话又可以推知丙也能获奖,这样得出4个人全都能获奖,不可能;
因此,只有甲没有获奖.
故答案为:甲
【分析】根据题意丙说的话进行分析可得丁获奖,进而分析甲的情况假设甲获奖进行推导得矛盾,即可得答案。
15.【答案】 戊戌
【解析】由题意,可得数列天干是以10为公差的等差数列,地支是以12为公差的等差数列,
从2017年到2078年经过了61年,且2017年为丁茜年,以2017年的天干和地支分别为首项,则 余 ,则2078年的天干为戊, 余 ,则2078年的天干为戌,
所以2078年为戊戌年。
【分析】首先根据题意得出数列天干是以10为公差的等差数列,地支是以12为公差的等差数列,以2017年的天干和地支分别为首项,由此得出结果。
16.【答案】 A
【解析】由乙说:我没去过C城市,则乙可能去过A城市或B城市,但甲说:我去过的城市比乙多,但没去过B城市,则乙只能是去过A,B中的任一个,再由丙说:我们三人去过同一城市,则由此可判断乙去过的城市为A
【分析】由已知进行简单的推理,即可判断乙去过的城市为A.
17.【答案】
【解析】解:类比观察得,将莱布尼茨三角形的每一行都能提出倍数 ,
而相邻两项之和是上一行的两者相拱之数,所以类比式子 ,有 .
故答案为: .
【分析】这是一个考查类比推理的题目,解题的关键是仔细观察图中给出的莱布尼茨三角形,并从三解数阵中,找出行与行之间数的关系,探究规律并其表示出来.
18.【答案】
【解析】在平面中,设内切圆的圆心为 ,半径为 ,连结 ,则有
所以 ,类比到空间可得,设内切球的球心为 ,半径为 ,则有
所以四面体 的内切球的半径为 .
【分析】利用已知条件结合类比推理的方法,从而得出四面体 的内切球的半径。
19.【答案】 ②
【解析】解:对于①,因为N为 上一点,所以平面 与平面 所成二面角α即为平面 与平面 BCC1B1所成二面角β,显然β是固定角,故①正确;
对于②,假设BB上存在点P,使得C1P⊥平面EFB1C,则C1P⊥FB1 , 而FB1⊥B1C1 , 所以FB1⊥平面BB1C1C,显然错误,故②错误;
对于③, , 又 ,
所以 , 而 ,
连接DA1 , 则F到平面DB1C的距离即为F到A1D的距离,所以,
所以
所以 , 故③正确;
对于④,以D1为原点,分别以D1A1 , D1D,D1C1为x,y,z轴建立空间直角坐标系,
则C(0,2,2),F(2,0,1),M(x,0,0),
则
当 , 即 , 即时, ,
此时 , 故④正确
故答案为:②
【分析】根据二面角的平面角的定义可判断①,运用反证法结合直线与平面垂直的判定定理可判断②,根据棱锥的体积公式,结合点到平面的距离,运用等体积法可判断③,利用向量法结合向量数量积运算的坐标表示可判断④.
20.【答案】 ①③④
【解析】对于①, ,故①正确;
对于②,不妨设 ,
则由韦达定理知 是一元二次方程 的两个根,
由 ,可得 或 ,故②错;
对于③,不妨设 中 ,
由 得 ,
当 时,即有 ,
,于是 , 无解,即不存在满足条件的“复活集”A,故③正确;
对于④,当 时, ,故只能 , ,求得 ,
于是“复活集” A只有一个,为 ,
当 时,由 ,
即有 ,
也就是说“复活集”A存在的必要条件是 ,
事实上 ,矛盾,
当 时不存在“复活集”A,故④正确.
故答案为:①③④
【分析】根据已知中“复活集”的定义,结合韦达定理以及反证法,依次判断四个结论的正误,进而可得答案.
三、解答题
21.【答案】 (1)解: , 恒成立,即为 ,也就是 在 上恒成立.
令 , , ,
当 时, , 单调递减,当 时, , 单调递增,
在 时, 取到极小值也是最小值, ,
所以
(2)解:当 时, ,
当 时, 时, , 单调递减,当 时, , 单调递增,
∴ 时 取到极小值也是最小值,即 ,
当 时, , , 单调递增,
(3)证明:要证当 时, .即证当 时, .
由(2)知当 时,函数 在 处的最小值为 ,
令 .∴ ,由 得 ,
所以在 得函数,在 为减函数,所以 ,
当 时, .
即当 时,
【解析】【分析】(1) , 恒成立,即为 恒成立,可化为. 在 上恒成立, 令 , , 利用导数研究其单调性极值
与最值即可得出 a的取值范围;
(2) 当 时, , 求导,根据导数的符号可得出 的单调性,进而求得 在区间 的最小值;
(3)要证当 时, , 即证当 时, , 令 , , 由 得 , 在 为减函数,所以 , 进而证得 .
22.【答案】 解:记 的面积依次为 ,
平面 与 所成角依次为 ,
点 到平面 的距离为 分别表示内切球与外接球的半径,内切球的球心为 ,
直角三角形 直角四面体
条件
结论1
结论2
结论3
结论4
结论5
证明:设 ,
过 作 ,垂足为 ,联结 ,过 作 ,垂足为 ,
易证: , 平面 ,则 ,
结论1: ,
在 中, ,
s
;
结论2: ,
∴ 。
同理, ,
∴ ;
结论3:∵ ,∴ ,
又 ,
∴
结论4: ,
∴ .
从而 ,即 ;
结论5:将直角四面体 补形成为以 为长、宽、高的长方体,
则长方体的体对角线即为直角四面体ABCD的外接球的直径,即 .
