黑龙江省绥化一高2021-2022学年高一上学期期中考试数学试卷(Word版含答案)
文档属性
| 名称 | 黑龙江省绥化一高2021-2022学年高一上学期期中考试数学试卷(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 622.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-25 00:00:00 | ||
图片预览


文档简介
绥化一高2021-2022学年度第一学期期中考试高一年级
数学试题
时间:120分钟 总分:150分
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。
第Ⅰ卷
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知全集,集合,,则 =( )
A. B. C. D.
2.命题“,”的否定是( )
A., B.,
C., D.,
3.设,则( )
A. B. C. D.
4.下列四组函数中表示同一个函数的是( )
A. B.
C. D.
5.函数的单调递增区间是( )
A. B. C. D.
6.已知函数满足.若,则( )
A.2 B.1 C. D.0
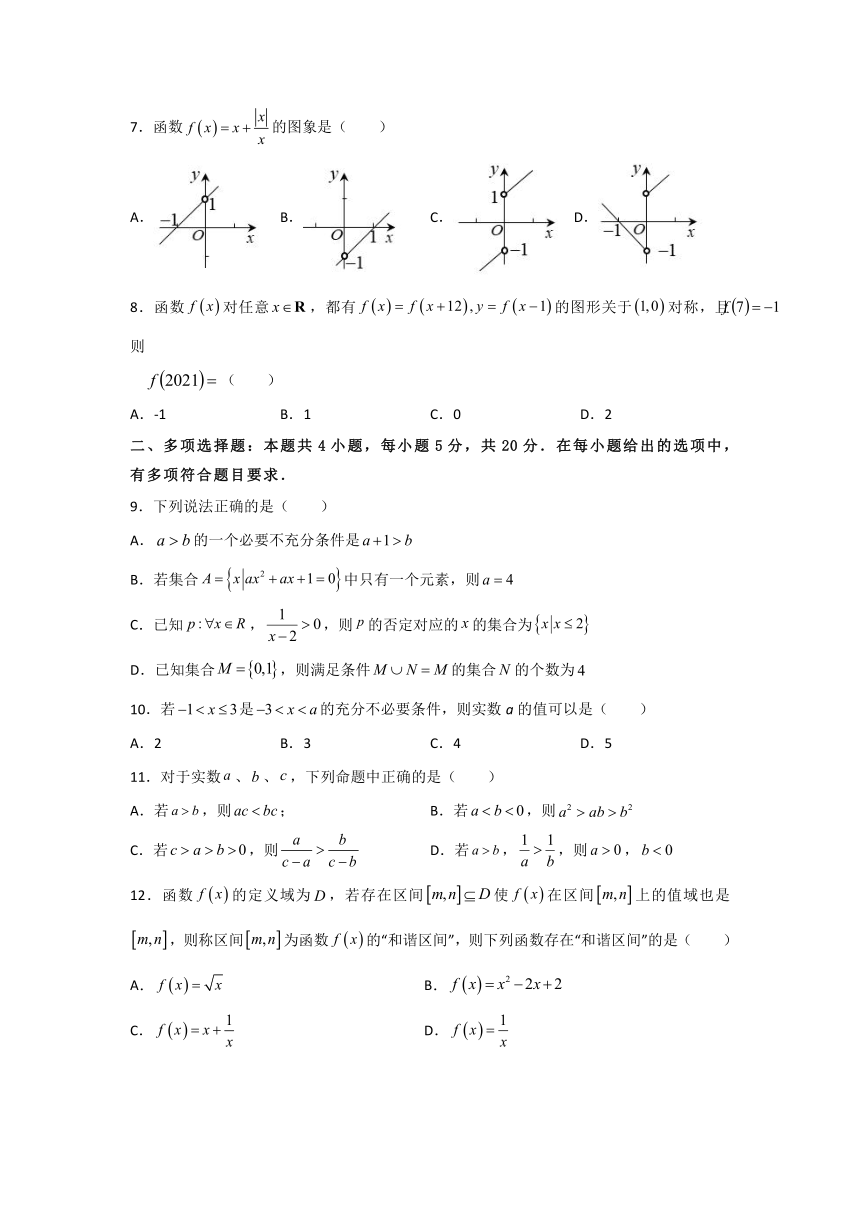
7.函数的图象是( )
A. B. C. D.
8.函数对任意,都有的图形关于对称,且 则
( )
A.-1 B.1 C.0 D.2
2、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.
9.下列说法正确的是( )
A.的一个必要不充分条件是
B.若集合中只有一个元素,则
C.已知,,则的否定对应的的集合为
D.已知集合,则满足条件的集合的个数为
10.若是的充分不必要条件,则实数a的值可以是( )
A.2 B.3 C.4 D.5
11.对于实数、、,下列命题中正确的是( )
A.若,则; B.若,则
C.若,则 D.若,,则,
12.函数的定义域为,若存在区间使在区间上的值域也是,则称区间为函数的“和谐区间”,则下列函数存在“和谐区间”的是( )
A. B.
C. D.
第Ⅱ卷
3、填空题:本大题共4小题,每小题5分.
13.已知,,且,则的最小值是___________
14.给出以下命题:
①若集合A={x,y},B={0,x2},A=B,则x=1,y=0;
②若函数f(x)的定义域为(-1,1),则函数f(2x+1)的定义域为(-1,0)
③函数f(x)=的单调递减区间是(-∞,0)∪(0,+∞)
其中正确的命题有___________.(写出所有正确命题的序号)
15.已知函数是定义在区间上的减函数,若 ,则实数的取值范围是
16.若不等式对任意恒成立,则实数的取值范围是
四、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(10分)
(1)求解不等式组
(2)已知,,求的取值范围.
18.(12分)
已知集合,或.
(1)当时,求; (2)是的充分不必要条件,求实数的取值范围.
19. (12分)某养殖公司欲将一批冷鲜肉用冷藏汽车从甲地运往相距120千米的乙地,运费为每小时60元,装卸费为1000元,冷鲜肉在运输途中的损耗费(单位:元)是汽车速度值的2倍.(说明:运输的总费用=运费+装卸费+损耗费)
(1)写出运输的总费用元与汽车速度的函数关系,并求汽车速度为每小时50千米,运输的总费用;
(2)求汽车行驶速度为何值时,使运输的总费用最小,最小值为多少?
20.(12分)
已知定义在区间上的函数为奇函数.
(1)求实数的值; (2)判断并证明函数在区间上的单调性.
21.(12分)
已知是二次函数,且满足
(1)求函数的解析式
(2)设,当时,求函数的最小值.
22.(12分)
已知函数的定义域为,且对任意 ,都有,且当时,恒成立.
(1)证明:函数是奇函数;
(2)在定义域上单调递减;
(3),求的取值范围.
高一年级数学试题答案:
1.C 2.C 3.B 4.D 5.B 6. C 7.C 8.B
9.ABCD 10.CD 11.BCD 12.ABD
13.12 14.①② 15. 16.
17.(1)或(2)
18.(1)或;(2)
(1)当时, 因为或,
所以或;
(2)因为或,所以.
因为“”是的充分不必要条件,所以是的真子集
当时,符合题意,此时有,解得:a<0.
当时,要使是的真子集,只需,解得:
综上:a<1.即实数的取值范围.
19.(1)(元);(2).
(1)依题意可得,
当汽车的速度为每小时50千米时,运输的总费用为:(元);
(2)设汽车行驶的速度为,
由题意可得:
故汽车行驶速度为时,,使运输的总费用最小。
20.(1);(2)在区间上是增函数,见解析;(3)
(1)由题意,函数是在区间上的奇函数,所以,
即函数,经检验符合题意,所以实数的值.
(2)设,则,
因为, 则,
所以,即,
所以函数在区间上是增函数.
20.(1)(2)
(1)设,∵,
∴,
即,所以,
解得,∴.
(2)由题意得,对称轴为直线,
①当即时,函数在单调递增;
②当即时,函数在单调递减,在单调递增,
,
综上:
22.(1)见解析;(2)见解析;(3)
(1)证明: ,
令,,则.
令,,,
即,而,
,即函数是奇函数;
(2)设,则,
当时,恒成立,则,
,
函数是上的减函数;
(3)由,
可得,又函数是奇函数,
∴,
∵在定义域上单调递减
∴ ,解得,∴,
解得,,故的取值范围.
数学试题
时间:120分钟 总分:150分
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。
第Ⅰ卷
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知全集,集合,,则 =( )
A. B. C. D.
2.命题“,”的否定是( )
A., B.,
C., D.,
3.设,则( )
A. B. C. D.
4.下列四组函数中表示同一个函数的是( )
A. B.
C. D.
5.函数的单调递增区间是( )
A. B. C. D.
6.已知函数满足.若,则( )
A.2 B.1 C. D.0
7.函数的图象是( )
A. B. C. D.
8.函数对任意,都有的图形关于对称,且 则
( )
A.-1 B.1 C.0 D.2
2、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.
9.下列说法正确的是( )
A.的一个必要不充分条件是
B.若集合中只有一个元素,则
C.已知,,则的否定对应的的集合为
D.已知集合,则满足条件的集合的个数为
10.若是的充分不必要条件,则实数a的值可以是( )
A.2 B.3 C.4 D.5
11.对于实数、、,下列命题中正确的是( )
A.若,则; B.若,则
C.若,则 D.若,,则,
12.函数的定义域为,若存在区间使在区间上的值域也是,则称区间为函数的“和谐区间”,则下列函数存在“和谐区间”的是( )
A. B.
C. D.
第Ⅱ卷
3、填空题:本大题共4小题,每小题5分.
13.已知,,且,则的最小值是___________
14.给出以下命题:
①若集合A={x,y},B={0,x2},A=B,则x=1,y=0;
②若函数f(x)的定义域为(-1,1),则函数f(2x+1)的定义域为(-1,0)
③函数f(x)=的单调递减区间是(-∞,0)∪(0,+∞)
其中正确的命题有___________.(写出所有正确命题的序号)
15.已知函数是定义在区间上的减函数,若 ,则实数的取值范围是
16.若不等式对任意恒成立,则实数的取值范围是
四、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(10分)
(1)求解不等式组
(2)已知,,求的取值范围.
18.(12分)
已知集合,或.
(1)当时,求; (2)是的充分不必要条件,求实数的取值范围.
19. (12分)某养殖公司欲将一批冷鲜肉用冷藏汽车从甲地运往相距120千米的乙地,运费为每小时60元,装卸费为1000元,冷鲜肉在运输途中的损耗费(单位:元)是汽车速度值的2倍.(说明:运输的总费用=运费+装卸费+损耗费)
(1)写出运输的总费用元与汽车速度的函数关系,并求汽车速度为每小时50千米,运输的总费用;
(2)求汽车行驶速度为何值时,使运输的总费用最小,最小值为多少?
20.(12分)
已知定义在区间上的函数为奇函数.
(1)求实数的值; (2)判断并证明函数在区间上的单调性.
21.(12分)
已知是二次函数,且满足
(1)求函数的解析式
(2)设,当时,求函数的最小值.
22.(12分)
已知函数的定义域为,且对任意 ,都有,且当时,恒成立.
(1)证明:函数是奇函数;
(2)在定义域上单调递减;
(3),求的取值范围.
高一年级数学试题答案:
1.C 2.C 3.B 4.D 5.B 6. C 7.C 8.B
9.ABCD 10.CD 11.BCD 12.ABD
13.12 14.①② 15. 16.
17.(1)或(2)
18.(1)或;(2)
(1)当时, 因为或,
所以或;
(2)因为或,所以.
因为“”是的充分不必要条件,所以是的真子集
当时,符合题意,此时有,解得:a<0.
当时,要使是的真子集,只需,解得:
综上:a<1.即实数的取值范围.
19.(1)(元);(2).
(1)依题意可得,
当汽车的速度为每小时50千米时,运输的总费用为:(元);
(2)设汽车行驶的速度为,
由题意可得:
故汽车行驶速度为时,,使运输的总费用最小。
20.(1);(2)在区间上是增函数,见解析;(3)
(1)由题意,函数是在区间上的奇函数,所以,
即函数,经检验符合题意,所以实数的值.
(2)设,则,
因为, 则,
所以,即,
所以函数在区间上是增函数.
20.(1)(2)
(1)设,∵,
∴,
即,所以,
解得,∴.
(2)由题意得,对称轴为直线,
①当即时,函数在单调递增;
②当即时,函数在单调递减,在单调递增,
,
综上:
22.(1)见解析;(2)见解析;(3)
(1)证明: ,
令,,则.
令,,,
即,而,
,即函数是奇函数;
(2)设,则,
当时,恒成立,则,
,
函数是上的减函数;
(3)由,
可得,又函数是奇函数,
∴,
∵在定义域上单调递减
∴ ,解得,∴,
解得,,故的取值范围.
同课章节目录
