2021-2022学年度沪科版八年级数学下册课件 17.1 一元二次方程(共15张PPT)
文档属性
| 名称 | 2021-2022学年度沪科版八年级数学下册课件 17.1 一元二次方程(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
数学与生活
回顾与思考
你能为一个矩形花园提供多种设计方案吗
一块四周镶有宽度相等的花边的地毯如下图,它的长为8m,宽为5m.如果地毯中央长方形图案的面积为18m2 ,则花边多宽
你怎么解决这个问题?
做一做
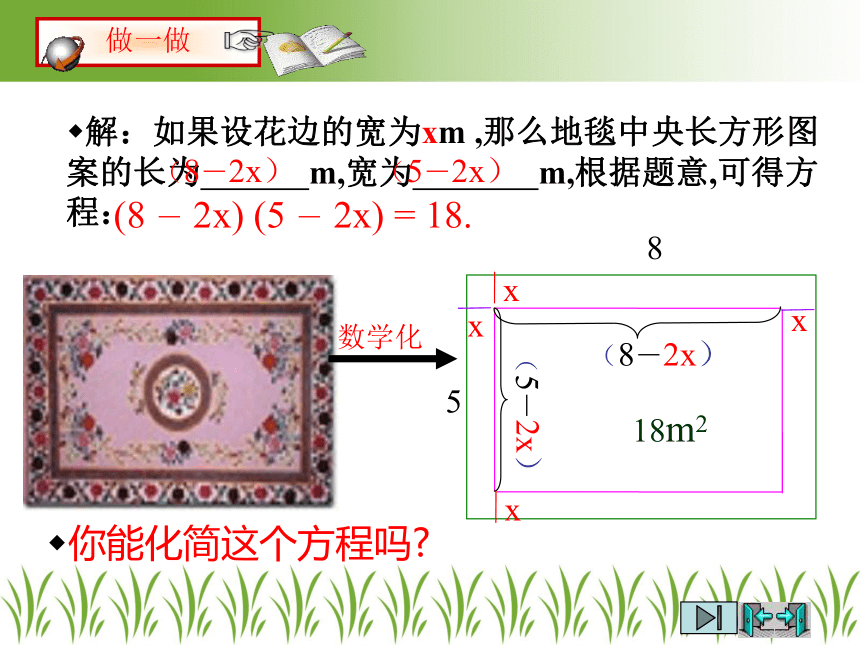
解:如果设花边的宽为xm ,那么地毯中央长方形图案的长为 m,宽为 m,根据题意,可得方程:
你能化简这个方程吗
(8-2x)
(5-2x)
(8 - 2x) (5 - 2x) = 18.
5
x
x
x
x
(8-2x)
(5-2x)
8
18m2
做一做
数学化
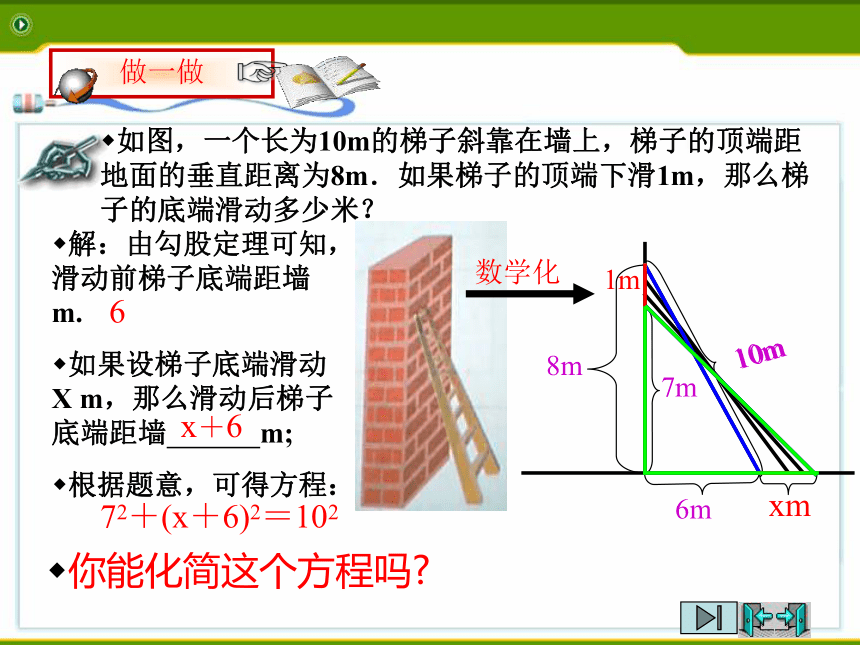
如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么梯子的底端滑动多少米?
解:由勾股定理可知,滑动前梯子底端距墙 m.
如果设梯子底端滑动X m,那么滑动后梯子底端距墙 m;
根据题意,可得方程:
你能化简这个方程吗
做一做
6
x+6
72+(x+6)2=102
xm
8m
10m
7m
6m
10m
数学化
1m
上面的方程都是只含有一个未知数x,并且未知数的最高次数是2的整式方程,叫做一元二次方程.
一元二次方程的概念
由上面两个问题,我们可以得到两个方程:
一元二次方程的一般形式:
ax2+bx+c=0(a≠0).
其中ax2叫做二次项, a是二次项系数;bx叫做一次项, b是一次项系数; c是常数项.除a≠0的限制外,a、b、c可以是任意实数.
(8-2x)(5-2x)=18;
即 2x2 - 13x + 11 = 0 .
( x+6)2+72=102
即 x2 +12 x -15 =0.
上述两个方程有什么共同特点?
“行家”看“门道”
下列方程哪些是一元二次方程
(2)2x2-5xy+6y=0
(5)x2+2x-3=1+x2
(1)7x2-6x=0
解: (1)、 (4)
(3)2x2- -1 =0
-
1
3x
(4) =0
-
y2
2
内涵与外延
1.关于x的方程(k-3)x2 + 2x-1=0,当k 时,是一元二次方程.
2.关于x的方程(k2-1)x2 + 2 (k-1) x + 2k + 2=0,当k 时,是一元二次方程.当k 时,是一元一次方程.
想一想:
≠3
≠±1
=-1
解:设竹竿的长为x尺,则门的宽 度为 尺,长为 尺,依题意得方程:
培养能力之源泉
1.从前有一天,一个醉汉拿着竹竿进屋,横拿竖拿都进不去,横着比门框宽4尺,竖着比门框高2尺,另一个醉汉教他沿着门的两个对角斜着拿竿,这个醉汉一试,不多不少刚好进去了.你知道竹竿有多长吗?请根据这一问题列出方程.
(x-4)2+ (x-2)2= x2
即
x2-12 x +20 = 0
4尺
2尺
x
x-4
x-2
数学化
(x-4)
(x-2)
2.把方程(3x+2)2=4(x-3)2化成一元二次方程的一般形式,并写出它的二次项系数、一次项系数和常数项.
解:将原方程化简为:
9x2+12x+4=4(x2-6x+9)
9x2+12x+4=
9x2
5x2 + 36 x - 32=0
二次项系数为 ,
5
+ 36
- 32
一次项系数为 ,
常数项为 .
5
36
- 32
4 x2 -24x +36
- 4 x2
+ 24x
- 36
+ 12x
+ 4
=0
本节课你又学会了哪些新知识呢?
1.学习了什么是一元二次方程,以及它的一般形式ax2+bx+c=0(a≠0)和有关概念,如二次项、一次项、常数项、二次项系数、一次项系数.
2.会用一元二次方程表示实际生活中的数量关系
你准备如何去求方程中的未知数呢
小结 拓展
独立
作业
1.根据题意,列出方程:
(1)有一面积为54m2的长方形,将它的一边剪短5m,另一边剪短2m,恰好变成一个正方形,这个正方形的边长是多少?
解:设正方形的边长为xm,则原长方形的长为(x+5) m,宽为(x+2) m,依题意得方程:
(x+5) (x+2) =54
即
x2 + 7x-44 =0
2
5
x
x
X+5
X+2
54m2
(2)三个连续整数两两相乘,再求和,结果为242,这三个数分别是多少?
x (x+1) + x(x+2) + (x+1) (x+2) =242.
x2 +2x-8 0=0.
即
解:设第一个数为x,则另两个数分别为x+1, x+2,依题意得方程:
2.把下列方程化为一元二次方程的形式,并写出它的二次项系数、一次项系数和常数项:
方 程 一般形式 二次项
系 数 一次项
系 数 常数项
3x2=5x-1
(x+2)(x -1)=6
4-7x2=0
3x2-5x+1=0
x2 + x-8=0
-7x2 +0 x+4=0
3
-5
+1
1
+1
-8
-7
0
4
3
-5
1
1
1
-8
-7
0
4
或7x2 - 4=0
7
0
- 4
-7x2 +4=0或
学而不思则罔,思而不学则殆。
——孔子
数学与生活
回顾与思考
你能为一个矩形花园提供多种设计方案吗
一块四周镶有宽度相等的花边的地毯如下图,它的长为8m,宽为5m.如果地毯中央长方形图案的面积为18m2 ,则花边多宽
你怎么解决这个问题?
做一做
解:如果设花边的宽为xm ,那么地毯中央长方形图案的长为 m,宽为 m,根据题意,可得方程:
你能化简这个方程吗
(8-2x)
(5-2x)
(8 - 2x) (5 - 2x) = 18.
5
x
x
x
x
(8-2x)
(5-2x)
8
18m2
做一做
数学化
如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么梯子的底端滑动多少米?
解:由勾股定理可知,滑动前梯子底端距墙 m.
如果设梯子底端滑动X m,那么滑动后梯子底端距墙 m;
根据题意,可得方程:
你能化简这个方程吗
做一做
6
x+6
72+(x+6)2=102
xm
8m
10m
7m
6m
10m
数学化
1m
上面的方程都是只含有一个未知数x,并且未知数的最高次数是2的整式方程,叫做一元二次方程.
一元二次方程的概念
由上面两个问题,我们可以得到两个方程:
一元二次方程的一般形式:
ax2+bx+c=0(a≠0).
其中ax2叫做二次项, a是二次项系数;bx叫做一次项, b是一次项系数; c是常数项.除a≠0的限制外,a、b、c可以是任意实数.
(8-2x)(5-2x)=18;
即 2x2 - 13x + 11 = 0 .
( x+6)2+72=102
即 x2 +12 x -15 =0.
上述两个方程有什么共同特点?
“行家”看“门道”
下列方程哪些是一元二次方程
(2)2x2-5xy+6y=0
(5)x2+2x-3=1+x2
(1)7x2-6x=0
解: (1)、 (4)
(3)2x2- -1 =0
-
1
3x
(4) =0
-
y2
2
内涵与外延
1.关于x的方程(k-3)x2 + 2x-1=0,当k 时,是一元二次方程.
2.关于x的方程(k2-1)x2 + 2 (k-1) x + 2k + 2=0,当k 时,是一元二次方程.当k 时,是一元一次方程.
想一想:
≠3
≠±1
=-1
解:设竹竿的长为x尺,则门的宽 度为 尺,长为 尺,依题意得方程:
培养能力之源泉
1.从前有一天,一个醉汉拿着竹竿进屋,横拿竖拿都进不去,横着比门框宽4尺,竖着比门框高2尺,另一个醉汉教他沿着门的两个对角斜着拿竿,这个醉汉一试,不多不少刚好进去了.你知道竹竿有多长吗?请根据这一问题列出方程.
(x-4)2+ (x-2)2= x2
即
x2-12 x +20 = 0
4尺
2尺
x
x-4
x-2
数学化
(x-4)
(x-2)
2.把方程(3x+2)2=4(x-3)2化成一元二次方程的一般形式,并写出它的二次项系数、一次项系数和常数项.
解:将原方程化简为:
9x2+12x+4=4(x2-6x+9)
9x2+12x+4=
9x2
5x2 + 36 x - 32=0
二次项系数为 ,
5
+ 36
- 32
一次项系数为 ,
常数项为 .
5
36
- 32
4 x2 -24x +36
- 4 x2
+ 24x
- 36
+ 12x
+ 4
=0
本节课你又学会了哪些新知识呢?
1.学习了什么是一元二次方程,以及它的一般形式ax2+bx+c=0(a≠0)和有关概念,如二次项、一次项、常数项、二次项系数、一次项系数.
2.会用一元二次方程表示实际生活中的数量关系
你准备如何去求方程中的未知数呢
小结 拓展
独立
作业
1.根据题意,列出方程:
(1)有一面积为54m2的长方形,将它的一边剪短5m,另一边剪短2m,恰好变成一个正方形,这个正方形的边长是多少?
解:设正方形的边长为xm,则原长方形的长为(x+5) m,宽为(x+2) m,依题意得方程:
(x+5) (x+2) =54
即
x2 + 7x-44 =0
2
5
x
x
X+5
X+2
54m2
(2)三个连续整数两两相乘,再求和,结果为242,这三个数分别是多少?
x (x+1) + x(x+2) + (x+1) (x+2) =242.
x2 +2x-8 0=0.
即
解:设第一个数为x,则另两个数分别为x+1, x+2,依题意得方程:
2.把下列方程化为一元二次方程的形式,并写出它的二次项系数、一次项系数和常数项:
方 程 一般形式 二次项
系 数 一次项
系 数 常数项
3x2=5x-1
(x+2)(x -1)=6
4-7x2=0
3x2-5x+1=0
x2 + x-8=0
-7x2 +0 x+4=0
3
-5
+1
1
+1
-8
-7
0
4
3
-5
1
1
1
-8
-7
0
4
或7x2 - 4=0
7
0
- 4
-7x2 +4=0或
学而不思则罔,思而不学则殆。
——孔子
