2021-2022学年度沪科版八年级数学下册课件 17.5 一元二次方程的应用(共14张PPT)
文档属性
| 名称 | 2021-2022学年度沪科版八年级数学下册课件 17.5 一元二次方程的应用(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 817.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 09:39:43 | ||
图片预览




文档简介
(共14张PPT)
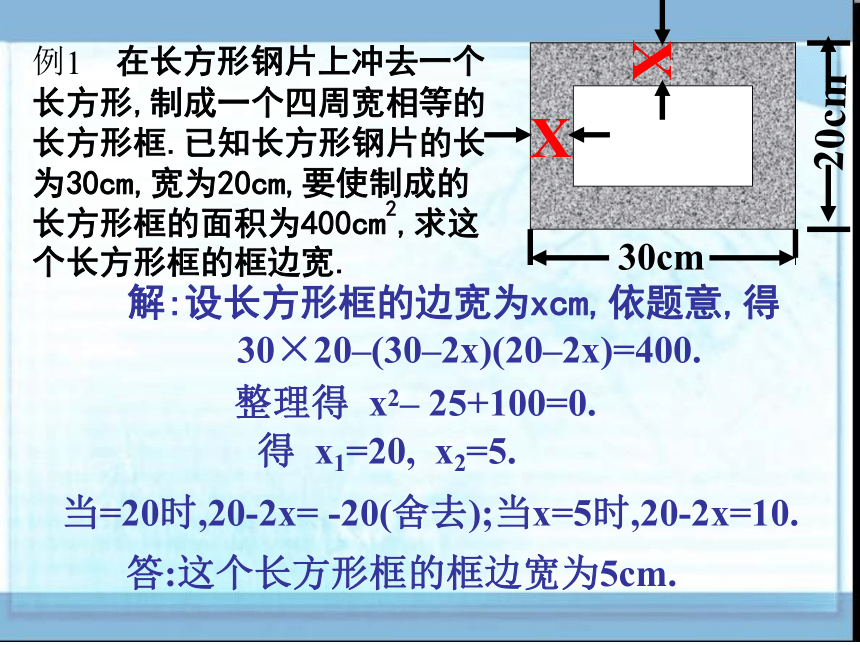
例1 在长方形钢片上冲去一个长方形,制成一个四周宽相等的长方形框.已知长方形钢片的长为30cm,宽为20cm,要使制成的长方形框的面积为400cm2,求这个长方形框的框边宽.
X
X
30cm
20cm
解:设长方形框的边宽为xcm,依题意,得
30×20–(30–2x)(20–2x)=400.
整理得 x2– 25+100=0.
得 x1=20, x2=5.
当=20时,20-2x= -20(舍去);当x=5时,20-2x=10.
答:这个长方形框的框边宽为5cm.
列方程解应用题的一般步骤是:
1.审:审清题意:已知什么,求什么
2.设:设未知数,语句要完整,
有单位(同一)的要注明单位;
3.列:列代数式,找出相等关系列方程;
4.解:解所列的方程;
5.验:是否是所列方程的根;是否符合题意;
6.答:答案也必需是完整的语句,
注明单位且要贴近生活.
列方程解应用题的关键是:找出相等关系.
归纳 总结
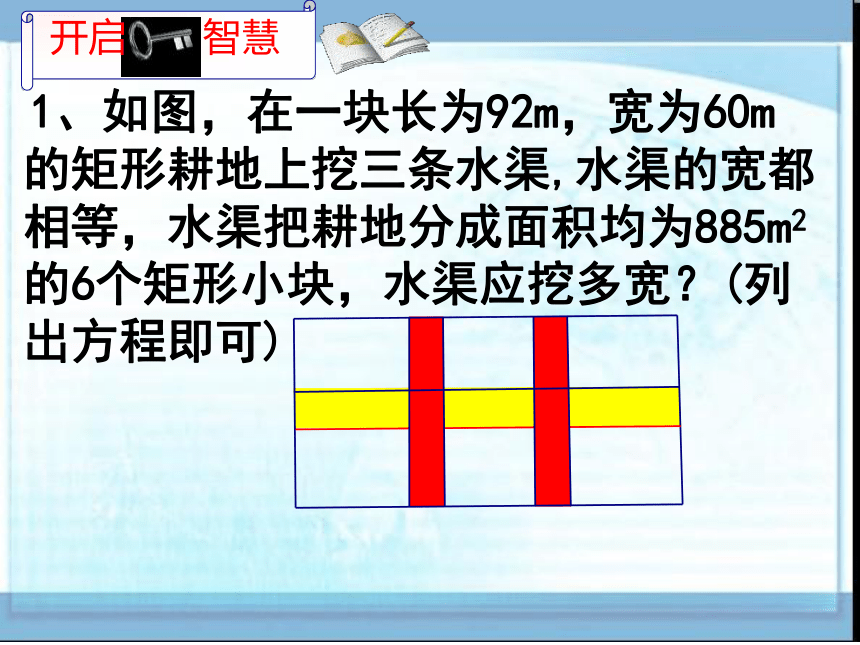
1、如图,在一块长为92m,宽为60m的矩形耕地上挖三条水渠,水渠的宽都相等,水渠把耕地分成面积均为885m2的6个矩形小块,水渠应挖多宽?(列出方程即可)
开启 智慧
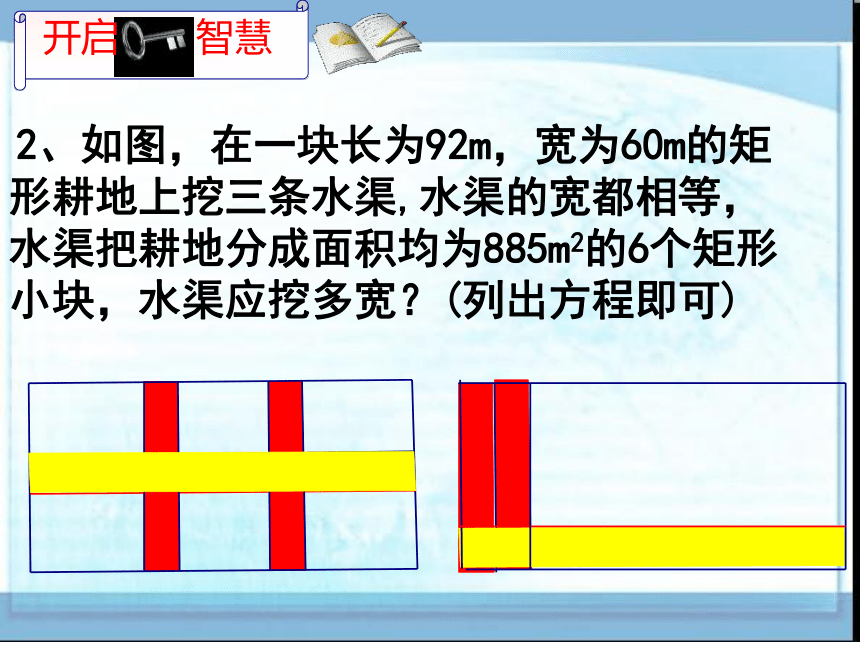
2、如图,在一块长为92m,宽为60m的矩形耕地上挖三条水渠,水渠的宽都相等,水渠把耕地分成面积均为885m2的6个矩形小块,水渠应挖多宽?(列出方程即可)
开启 智慧
例2 某工厂一月份的产值是5万元, 三月份的产值是7.2万元, 求月平均增长率是多少
解:设月平均增长率为X,依题意,得
5(1+X)2=7.2,
(1+X)2=1.44,即1+X=±1.2,
所以X1=0.2,X2=-2.2
答:月平均增长率为20%.
由于增长率不可能为负.所以X2=-2.2不符合题意,舍去.因此符合本题的X为X=0.2=20%.
例3 北京市政府为迎接2008年奥运会,决定改善城市容貌,绿化环境,计划经过两年时间,将城市绿地面积增加44 %,求这两年平均每年绿地面积增长率.
2011年的数量为A,2012年的数量为B,经过两个时间单位,求平均增长率x。
某季度数量为B,头一个月数量为A,求后两个月的增长率x.
2011年的数量A,经过两个时间单位后数量增加m%,求平均增长率x.
比较
A
2011年
A(1+x)
2012年
A(1+x)2
2013年
A
A(1+m%)
增加m%
=
=
A
+
A(1+x)
+
A(1+x)2
=
B
1、党的十六大提出全面建设小康社会,加快推进社会主义现代化建设,力争国民生产总值到2020年比2000年翻两番,在本世纪的头二十年(2001年至2020年),要实现这一目标,以十年为单位计算,设每个十年的国民生产总值的平均增长率为x,那么x满足的方程为_____________.
(1+x)2=4
2、某经济开发区今年一月份工业产值达50亿元,第一季度总产值达175亿元,问二、三月份平均每月的增长率为多少?设平均每月增长率为x,根据题意得方程:________________________
50+50(1+x)+50(1+x) 2=175
3、新亚商场销售某种冰箱,每台进价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销价每降低50元时,平均每天能多售4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元
回味无穷
小结 拓展
列方程解应用题的一般步骤是:
1.审:审清题意:已知什么,求什么
2.设:设未知数,语句要完整,有单位(同一)的要注明单位;
3.列:列代数式,找出相等关系列方程;
4.解:解所列的方程;
5.验:是否是所列方程的根;是否符合题意;
6.答:答案也必需是完整的语句,注明单位且要贴近生活.
列方程解应用题的关键是: 找出相等关系.
关于两次平均增长(降低)率问题的一般关系:
A(1±x)2=B(其中A表示基数,x表表示增长(或降低)率,B表示新数)
思考:如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC向点C以2cm/s,的速度移动,如果P、Q分别从A、B同时出发,那么几秒后五边形APQCD的面积为64cm2?
学而不思则罔,思而不学则殆。
——孔子
例1 在长方形钢片上冲去一个长方形,制成一个四周宽相等的长方形框.已知长方形钢片的长为30cm,宽为20cm,要使制成的长方形框的面积为400cm2,求这个长方形框的框边宽.
X
X
30cm
20cm
解:设长方形框的边宽为xcm,依题意,得
30×20–(30–2x)(20–2x)=400.
整理得 x2– 25+100=0.
得 x1=20, x2=5.
当=20时,20-2x= -20(舍去);当x=5时,20-2x=10.
答:这个长方形框的框边宽为5cm.
列方程解应用题的一般步骤是:
1.审:审清题意:已知什么,求什么
2.设:设未知数,语句要完整,
有单位(同一)的要注明单位;
3.列:列代数式,找出相等关系列方程;
4.解:解所列的方程;
5.验:是否是所列方程的根;是否符合题意;
6.答:答案也必需是完整的语句,
注明单位且要贴近生活.
列方程解应用题的关键是:找出相等关系.
归纳 总结
1、如图,在一块长为92m,宽为60m的矩形耕地上挖三条水渠,水渠的宽都相等,水渠把耕地分成面积均为885m2的6个矩形小块,水渠应挖多宽?(列出方程即可)
开启 智慧
2、如图,在一块长为92m,宽为60m的矩形耕地上挖三条水渠,水渠的宽都相等,水渠把耕地分成面积均为885m2的6个矩形小块,水渠应挖多宽?(列出方程即可)
开启 智慧
例2 某工厂一月份的产值是5万元, 三月份的产值是7.2万元, 求月平均增长率是多少
解:设月平均增长率为X,依题意,得
5(1+X)2=7.2,
(1+X)2=1.44,即1+X=±1.2,
所以X1=0.2,X2=-2.2
答:月平均增长率为20%.
由于增长率不可能为负.所以X2=-2.2不符合题意,舍去.因此符合本题的X为X=0.2=20%.
例3 北京市政府为迎接2008年奥运会,决定改善城市容貌,绿化环境,计划经过两年时间,将城市绿地面积增加44 %,求这两年平均每年绿地面积增长率.
2011年的数量为A,2012年的数量为B,经过两个时间单位,求平均增长率x。
某季度数量为B,头一个月数量为A,求后两个月的增长率x.
2011年的数量A,经过两个时间单位后数量增加m%,求平均增长率x.
比较
A
2011年
A(1+x)
2012年
A(1+x)2
2013年
A
A(1+m%)
增加m%
=
=
A
+
A(1+x)
+
A(1+x)2
=
B
1、党的十六大提出全面建设小康社会,加快推进社会主义现代化建设,力争国民生产总值到2020年比2000年翻两番,在本世纪的头二十年(2001年至2020年),要实现这一目标,以十年为单位计算,设每个十年的国民生产总值的平均增长率为x,那么x满足的方程为_____________.
(1+x)2=4
2、某经济开发区今年一月份工业产值达50亿元,第一季度总产值达175亿元,问二、三月份平均每月的增长率为多少?设平均每月增长率为x,根据题意得方程:________________________
50+50(1+x)+50(1+x) 2=175
3、新亚商场销售某种冰箱,每台进价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销价每降低50元时,平均每天能多售4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元
回味无穷
小结 拓展
列方程解应用题的一般步骤是:
1.审:审清题意:已知什么,求什么
2.设:设未知数,语句要完整,有单位(同一)的要注明单位;
3.列:列代数式,找出相等关系列方程;
4.解:解所列的方程;
5.验:是否是所列方程的根;是否符合题意;
6.答:答案也必需是完整的语句,注明单位且要贴近生活.
列方程解应用题的关键是: 找出相等关系.
关于两次平均增长(降低)率问题的一般关系:
A(1±x)2=B(其中A表示基数,x表表示增长(或降低)率,B表示新数)
思考:如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC向点C以2cm/s,的速度移动,如果P、Q分别从A、B同时出发,那么几秒后五边形APQCD的面积为64cm2?
学而不思则罔,思而不学则殆。
——孔子
