2021-2022学年度沪科版八年级数学下册课件 18.1 勾股定理(第1课时)(共15张PPT)
文档属性
| 名称 | 2021-2022学年度沪科版八年级数学下册课件 18.1 勾股定理(第1课时)(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览



文档简介
(共15张PPT)
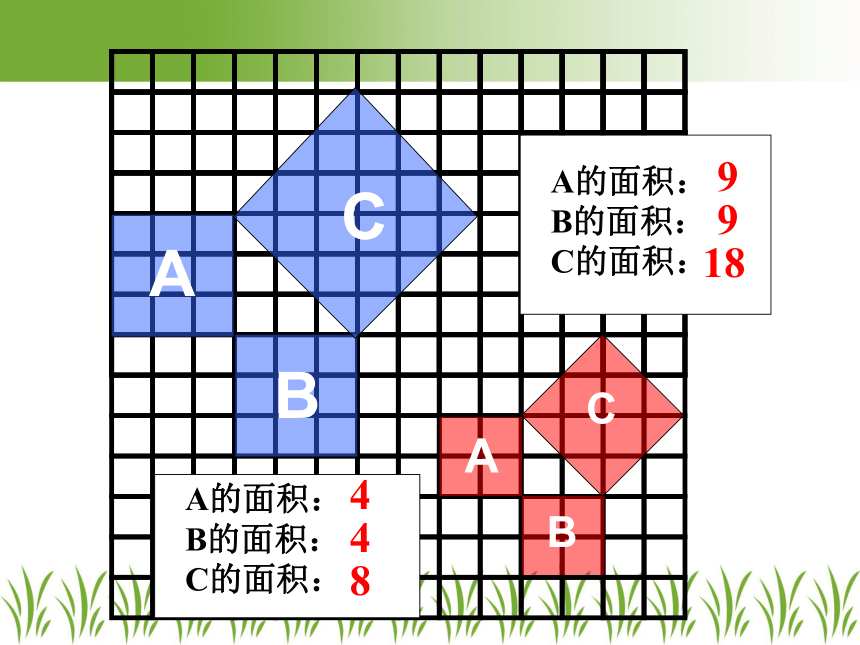
探索勾股定理
A
B
C
A
B
C
A的面积: B的面积: C的面积:
A的面积: B的面积: C的面积:
9
9
18
4
4
8
A
B
C
B
A
C
组图1
组图2
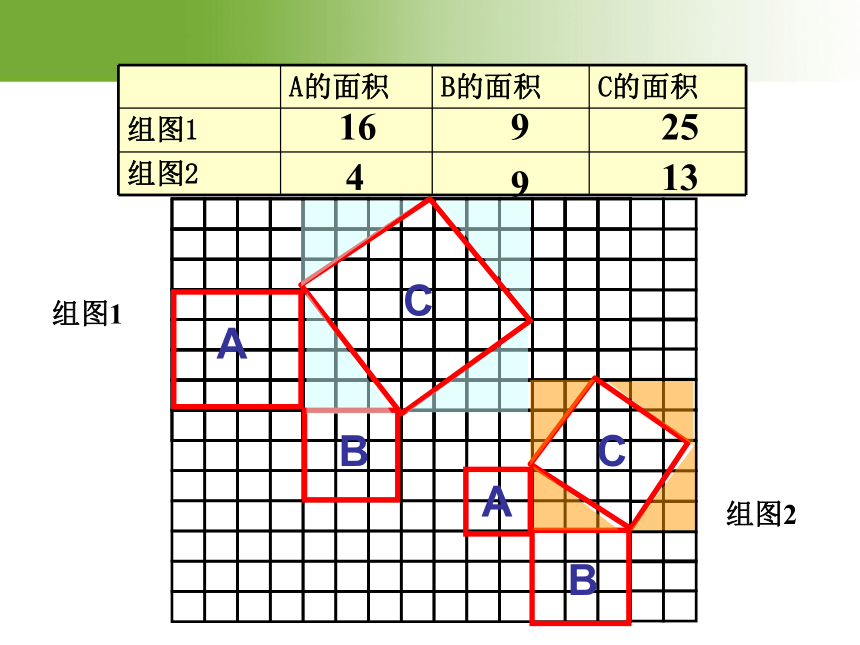
A的面积 B的面积 C的面积
组图1
组图2
16
9
25
4
9
13
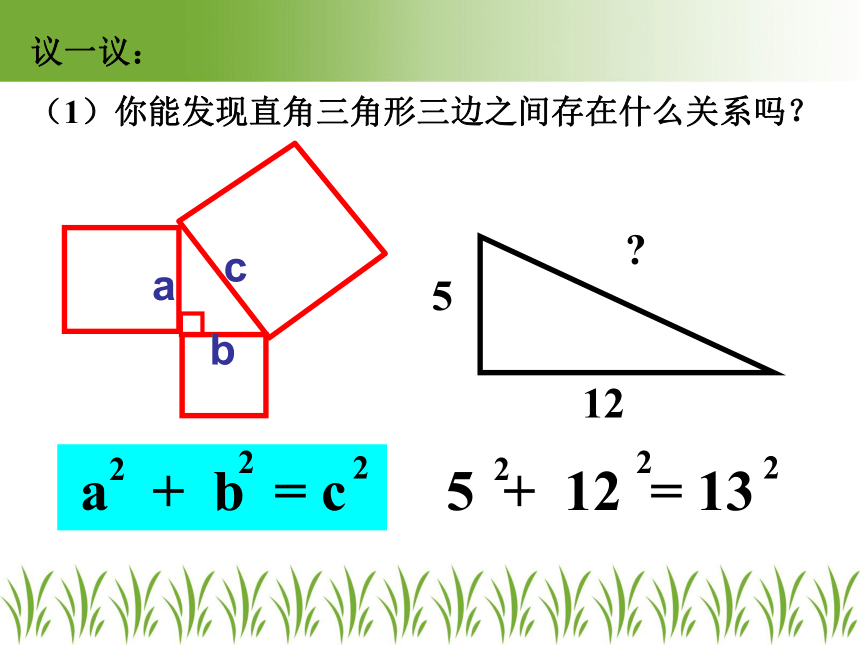
议一议:
(1)你能发现直角三角形三边之间存在什么关系吗?
a
b
c
a + b = c
2
2
2
5 + 12 = 13
2
2
2
12
5
勾股定理
如果直角三角形两直角边分别为 a 、 b ,斜边为c,
那么 a + b = c
即直角三角形两条直角边的平方和,等于斜边的平方.
2
2
2
a
b
c
勾
弦
股
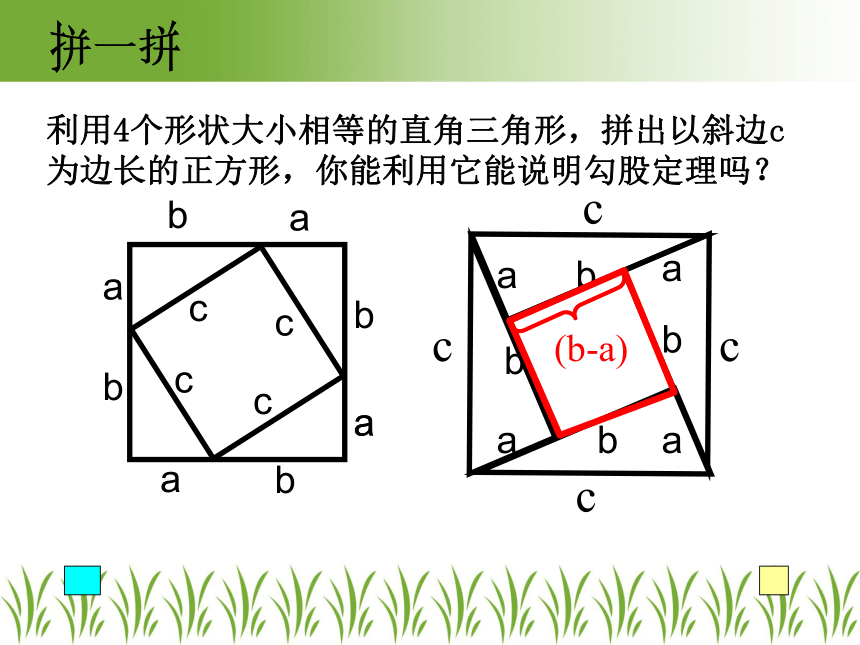
利用4个形状大小相等的直角三角形,拼出以斜边c为边长的正方形,你能利用它能说明勾股定理吗?
(b-a)
a
a
a
a
b
b
b
b
c
c
c
c
a
c
c
c
c
b
a
a
a
a
b
b
b
1、求下列字母所代表的正方形的面积。
225
400
A
225
81
B
解:正方形A的面积
=225+400
=625
解:正方形B的面积
=81+225
=306
2、求出下列直角三角形中未知边的长度:
3
4
x
5
13
y
解:由勾股定理得
x = 3 + 4 =25.
2
2
2
∵x>0,
∴x = 5.
解:由勾股定理得
y = 13 - 5 =144.
2
2
2
∵y>0,
∴y = 12.
3、下列阴影部分是一个正方形,求此正方形的面积.
15厘米
17厘米
解:设正方形的边长为x厘米 , 则
x2=172-152=64
答:正方形的面积是64平方厘米.
4、如图,一根旗杆在离地面9米处断裂,旗杆顶部落在离旗杆底部12米处,旗杆折断之前有多高?
9米
12米
A
B
思考:城市A要到达城市B必须经过C地的一条互相垂直的公路才能到达,为了城市发展的需要,政府决定在城市A、B之间建造一条最短的公路。如果你是工程师,如何建造?建成之后两个城市之间缩短了多少距离?
8公里
6公里
?
c
观察下图,判断图中三角形的三边是否满足a2 + b2 = c2
如图,分别以直角三角形三边为直径作三个半圆
这三个半圆的面积之间有什么关系?为什么?
再见!
课后要好好总结哦!
学而不思则罔,思而不学则殆。
——孔子
探索勾股定理
A
B
C
A
B
C
A的面积: B的面积: C的面积:
A的面积: B的面积: C的面积:
9
9
18
4
4
8
A
B
C
B
A
C
组图1
组图2
A的面积 B的面积 C的面积
组图1
组图2
16
9
25
4
9
13
议一议:
(1)你能发现直角三角形三边之间存在什么关系吗?
a
b
c
a + b = c
2
2
2
5 + 12 = 13
2
2
2
12
5
勾股定理
如果直角三角形两直角边分别为 a 、 b ,斜边为c,
那么 a + b = c
即直角三角形两条直角边的平方和,等于斜边的平方.
2
2
2
a
b
c
勾
弦
股
利用4个形状大小相等的直角三角形,拼出以斜边c为边长的正方形,你能利用它能说明勾股定理吗?
(b-a)
a
a
a
a
b
b
b
b
c
c
c
c
a
c
c
c
c
b
a
a
a
a
b
b
b
1、求下列字母所代表的正方形的面积。
225
400
A
225
81
B
解:正方形A的面积
=225+400
=625
解:正方形B的面积
=81+225
=306
2、求出下列直角三角形中未知边的长度:
3
4
x
5
13
y
解:由勾股定理得
x = 3 + 4 =25.
2
2
2
∵x>0,
∴x = 5.
解:由勾股定理得
y = 13 - 5 =144.
2
2
2
∵y>0,
∴y = 12.
3、下列阴影部分是一个正方形,求此正方形的面积.
15厘米
17厘米
解:设正方形的边长为x厘米 , 则
x2=172-152=64
答:正方形的面积是64平方厘米.
4、如图,一根旗杆在离地面9米处断裂,旗杆顶部落在离旗杆底部12米处,旗杆折断之前有多高?
9米
12米
A
B
思考:城市A要到达城市B必须经过C地的一条互相垂直的公路才能到达,为了城市发展的需要,政府决定在城市A、B之间建造一条最短的公路。如果你是工程师,如何建造?建成之后两个城市之间缩短了多少距离?
8公里
6公里
?
c
观察下图,判断图中三角形的三边是否满足a2 + b2 = c2
如图,分别以直角三角形三边为直径作三个半圆
这三个半圆的面积之间有什么关系?为什么?
再见!
课后要好好总结哦!
学而不思则罔,思而不学则殆。
——孔子
