2021-2022学年度沪科版八年级数学下册课件 19.2 平行四边形(第3课时)(共21张PPT)
文档属性
| 名称 | 2021-2022学年度沪科版八年级数学下册课件 19.2 平行四边形(第3课时)(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 647.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览


文档简介
(共21张PPT)
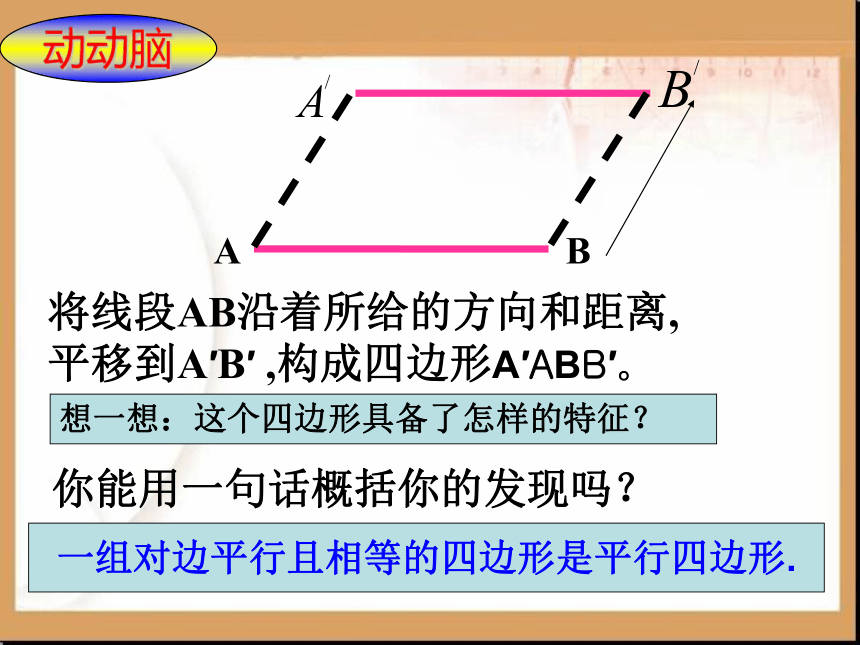
B
A
将线段AB沿着所给的方向和距离,
平移到A′B′ ,构成四边形A′ABB′。
动动脑
想一想:这个四边形具备了怎样的特征?
一组对边平行且相等的四边形是平行四边形.
你能用一句话概括你的发现吗?
一组对边平行且相等的四边形是平行四边形.
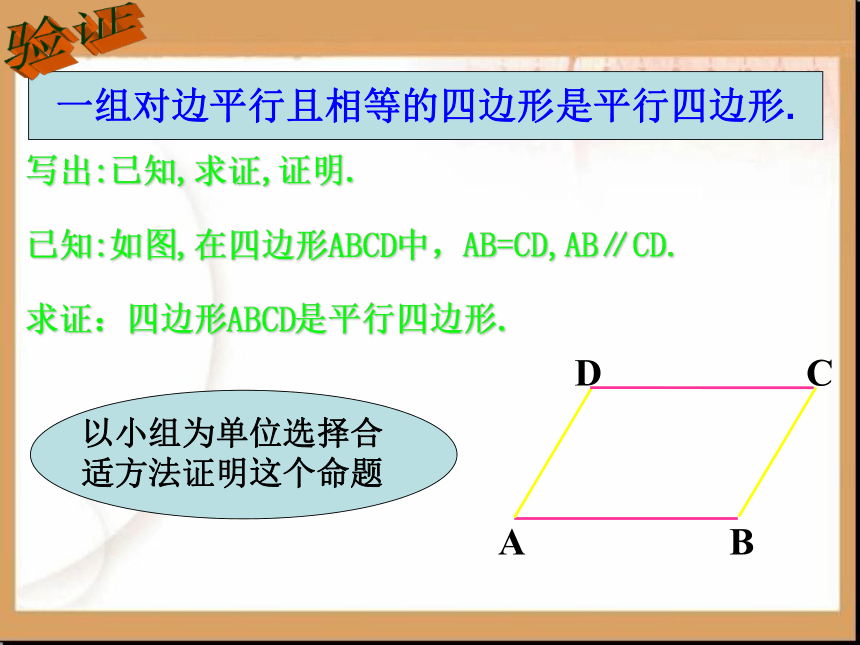
写出:已知,求证,证明.
已知:如图,在四边形ABCD中,AB=CD,AB∥CD.
求证:四边形ABCD是平行四边形.
以小组为单位选择合适方法证明这个命题
B
C
A
D
已知:如图,在四边形ABCD中,AB=CD,AB∥CD.
求证:四边形ABCD是平行四边形.
B
C
A
D
证明:
连接DB,
∵ AB∥CD,
∴∠CDB= ∠ABD.
在△CDB与△ABD中,
CD=AB,(已知)
∠CDB= ∠ABD,(已证)
DB=BD,(公共边)
∴△CDB≌△ABD.(SAS)
∴ ∠ADB= ∠CBD,
∴ AD∥BC.
∴四边形ABCD是平行四边行.
B
C
A
D
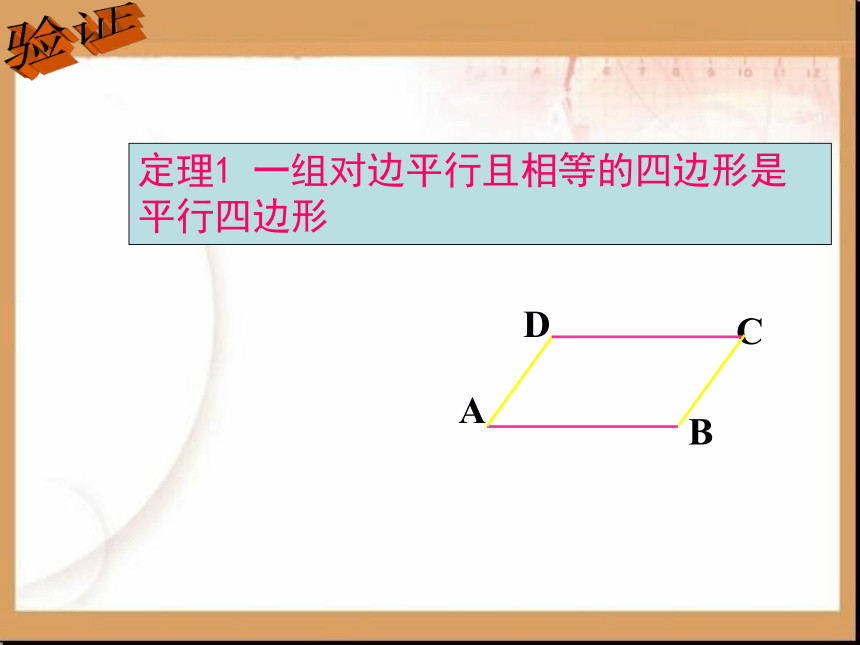
定理1 一组对边平行且相等的四边形是平行四边形
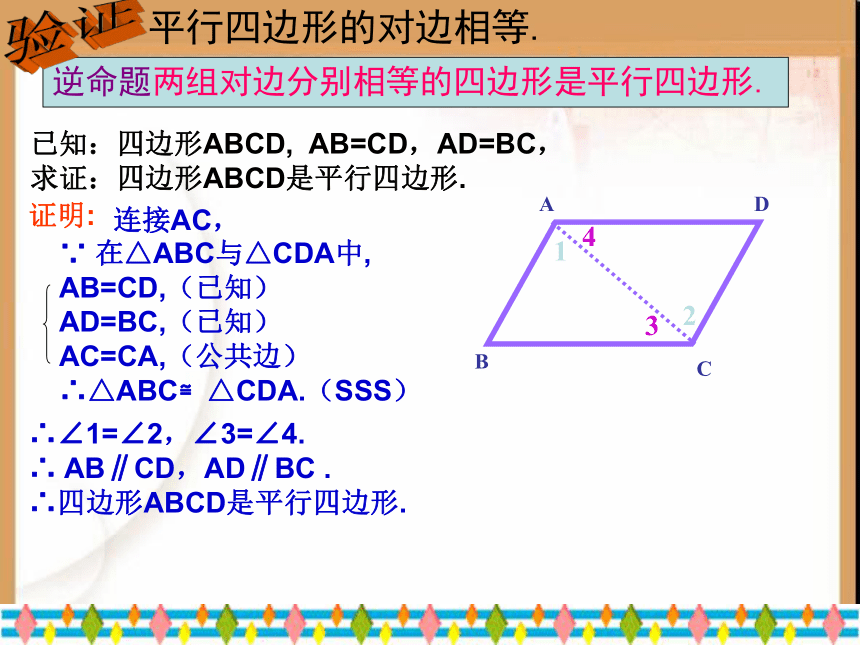
平行四边形的对边相等.
逆命题两组对边分别相等的四边形是平行四边形.
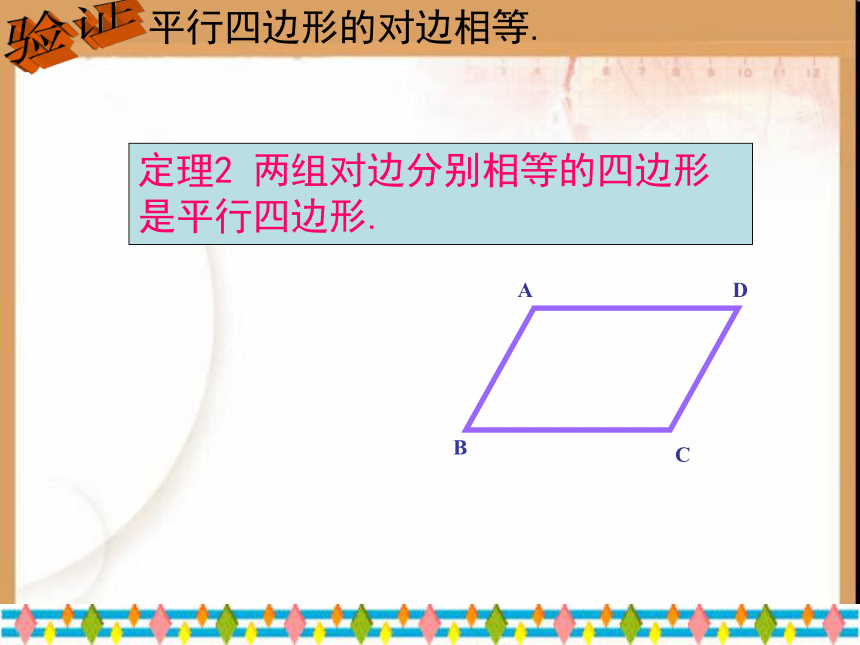
已知:四边形ABCD, AB=CD,AD=BC,
求证:四边形ABCD是平行四边形.
证明:
∵ 在△ABC与△CDA中,
AB=CD,(已知)
AD=BC,(已知)
AC=CA,(公共边)
∴△ABC≌△CDA.(SSS)
∴∠1=∠2,∠3=∠4.
∴ AB∥CD,AD∥BC .
∴四边形ABCD是平行四边形.
B
D
A
C
2
1
3
4
连接AC,
平行四边形的对边相等.
B
D
A
C
定理2 两组对边分别相等的四边形是平行四边形.
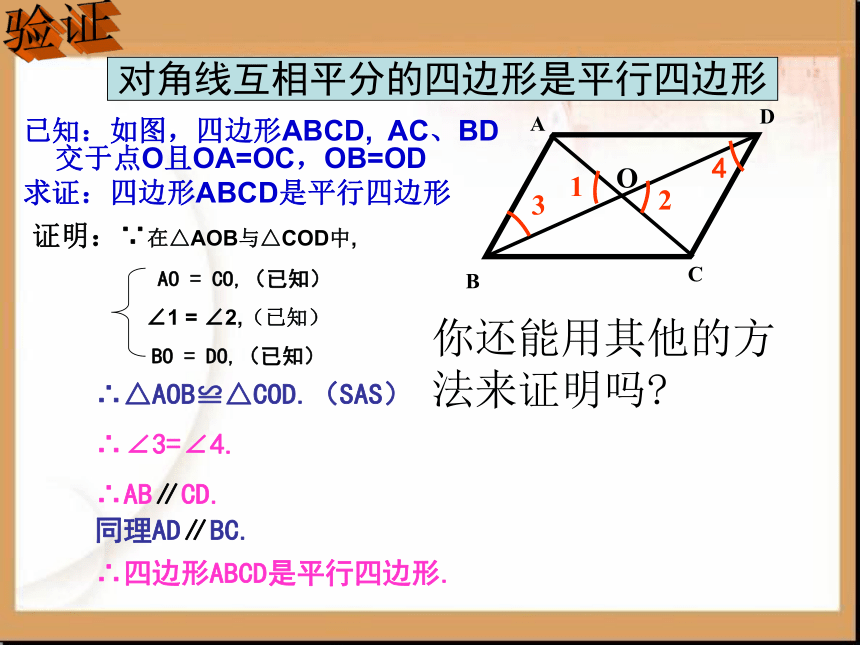
对角线互相平分的四边形是平行四边形
已知:如图,四边形ABCD, AC、BD交于点O且OA=OC,OB=OD
求证:四边形ABCD是平行四边形
B
D
A
C
O
4
2
1
3
证明:∵在△AOB与△COD中,
AO = CO,(已知)
∠1 = ∠2,(已知)
BO = DO,(已知)
∴△AOB≌△COD.(SAS)
∴∠3=∠4.
∴AB∥CD.
同理AD∥BC.
∴四边形ABCD是平行四边形.
你还能用其他的方法来证明吗
B
D
A
C
O
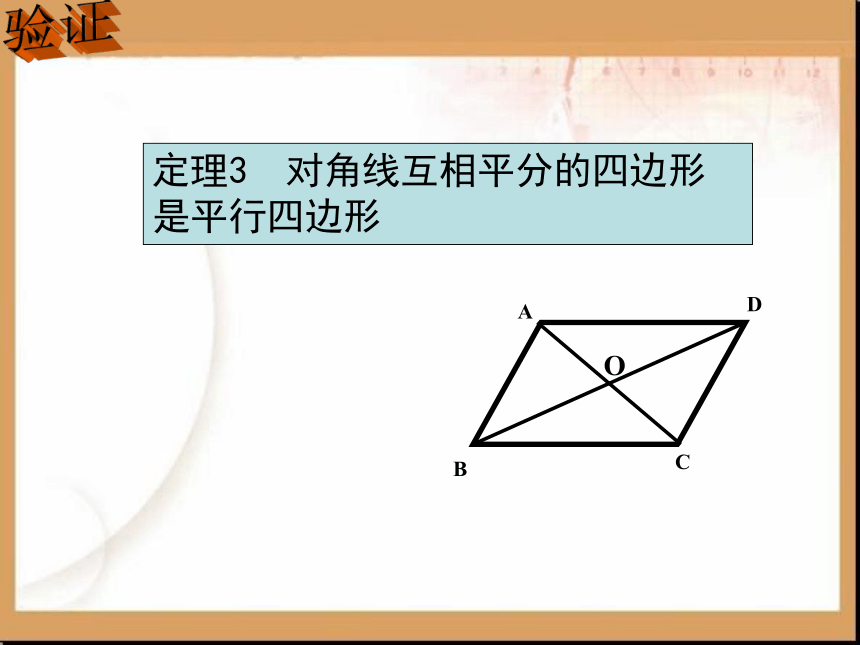
定理3 对角线互相平分的四边形是平行四边形
B
C
A
D
例1 已知:如图,点E、F是平行四边形对角线AB上的两点,且AE=CF.
求证:四边形DEBF是平行四边形.
E
F
O
证明:连接BD交AC于点O,
∵ 四边形ABCD是平行四边形,
∴AO=CO,BO=DO.
又∵AE=CF,
∴OE=OF。
∴四边形DEBF是平行四边形.
例2 如图,点D、E分别是△ABC的边AB、AC的中点,求证:DE∥BC且DE= BC.
A
B
C
D
E
B
C
A
D
E
F
证明:延长DE到F,使EF=DE,连接FC、DC、AF
∴四边形ADCF是平行四边形.
∴四边形DBCF是平行四边形.
∵AE=EC,
∴ CF∥DA,CF=DA.
∵ CF∥BD, CF=DA=BD.
∴DF∥BC,DF=BC.
又DE= DF,
∴DE= BC.
中位线定义:连接三角形两边中点的线段叫做三角形的中位线.
中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
1.如图,在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么当BC=____cm,CD=____cm时,四边形ABCD为平行四边形;
(2)若AC=10cm,BD=8cm,那么当AO=___cm,DO=___cm时,四边形ABCD为平行四边形.
2、下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.∠A=∠C,∠B=∠D
B.∠A=∠B=∠C=90 °
C.∠A+∠B=180°,∠B+∠C=180 °
D.∠A+∠B=180 °,∠C+∠D=180 °
A
B
C
D
D
3、下列条件中能判定一个四边形是平行四边形的条件是( )
①一组对边相等,且一组对角相等;
②一组对边相等且一条对角线平分另一条对角线;
③一组对角相等,且这一组对角的顶点所连结的对角线被另一条对角线平分;
④一组对角相等,且这一组对角的顶点所连结的对角线平分这组对角.
A.①和②
B.②和③
C.②和④
D.只有④
D
A
B
C
D
4、如图,在平行四边形ABCD的一组对边AD、BC上截取EF=MN,连接EM、FN,EM和FN有怎样的关系?为什么?
B
D
A
C
M
N
E
F
5.如图,点D、E、F分别是△ABC的边AB、BC、CA的中点,以这些点为顶点,你能在图中画出多少个平行四边形?
B
A
F
E
D
C
6.如图, A 、B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样测出A、B两点的实际距离?根据是什么?
A
B
C
小结
1、今天我们学行四边形的判定定理
2、三角形中位线的定义
3、三角形中位线定理
判定 文字语言 图形语言 符号语言
定义 两组对边分别平行的四边形是平行四边形
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
定理1 一组对边平行且相等的四边形是平行四边形 ∵AB=CD, AB∥CD,
∴四边形ABCD是平行四边形
定理2 两组对边分别相等的四边形是平等四边形
∵AB=CD,AD= BC ∴ 四边形ABCD是平行四边形
定理 3 对角线互相平分的四边形是平行四边形
∵OA=OC,OB=OD ∴四边形ABCD是平行四边形
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
O
学而不思则罔,思而不学则殆。
——孔子
B
A
将线段AB沿着所给的方向和距离,
平移到A′B′ ,构成四边形A′ABB′。
动动脑
想一想:这个四边形具备了怎样的特征?
一组对边平行且相等的四边形是平行四边形.
你能用一句话概括你的发现吗?
一组对边平行且相等的四边形是平行四边形.
写出:已知,求证,证明.
已知:如图,在四边形ABCD中,AB=CD,AB∥CD.
求证:四边形ABCD是平行四边形.
以小组为单位选择合适方法证明这个命题
B
C
A
D
已知:如图,在四边形ABCD中,AB=CD,AB∥CD.
求证:四边形ABCD是平行四边形.
B
C
A
D
证明:
连接DB,
∵ AB∥CD,
∴∠CDB= ∠ABD.
在△CDB与△ABD中,
CD=AB,(已知)
∠CDB= ∠ABD,(已证)
DB=BD,(公共边)
∴△CDB≌△ABD.(SAS)
∴ ∠ADB= ∠CBD,
∴ AD∥BC.
∴四边形ABCD是平行四边行.
B
C
A
D
定理1 一组对边平行且相等的四边形是平行四边形
平行四边形的对边相等.
逆命题两组对边分别相等的四边形是平行四边形.
已知:四边形ABCD, AB=CD,AD=BC,
求证:四边形ABCD是平行四边形.
证明:
∵ 在△ABC与△CDA中,
AB=CD,(已知)
AD=BC,(已知)
AC=CA,(公共边)
∴△ABC≌△CDA.(SSS)
∴∠1=∠2,∠3=∠4.
∴ AB∥CD,AD∥BC .
∴四边形ABCD是平行四边形.
B
D
A
C
2
1
3
4
连接AC,
平行四边形的对边相等.
B
D
A
C
定理2 两组对边分别相等的四边形是平行四边形.
对角线互相平分的四边形是平行四边形
已知:如图,四边形ABCD, AC、BD交于点O且OA=OC,OB=OD
求证:四边形ABCD是平行四边形
B
D
A
C
O
4
2
1
3
证明:∵在△AOB与△COD中,
AO = CO,(已知)
∠1 = ∠2,(已知)
BO = DO,(已知)
∴△AOB≌△COD.(SAS)
∴∠3=∠4.
∴AB∥CD.
同理AD∥BC.
∴四边形ABCD是平行四边形.
你还能用其他的方法来证明吗
B
D
A
C
O
定理3 对角线互相平分的四边形是平行四边形
B
C
A
D
例1 已知:如图,点E、F是平行四边形对角线AB上的两点,且AE=CF.
求证:四边形DEBF是平行四边形.
E
F
O
证明:连接BD交AC于点O,
∵ 四边形ABCD是平行四边形,
∴AO=CO,BO=DO.
又∵AE=CF,
∴OE=OF。
∴四边形DEBF是平行四边形.
例2 如图,点D、E分别是△ABC的边AB、AC的中点,求证:DE∥BC且DE= BC.
A
B
C
D
E
B
C
A
D
E
F
证明:延长DE到F,使EF=DE,连接FC、DC、AF
∴四边形ADCF是平行四边形.
∴四边形DBCF是平行四边形.
∵AE=EC,
∴ CF∥DA,CF=DA.
∵ CF∥BD, CF=DA=BD.
∴DF∥BC,DF=BC.
又DE= DF,
∴DE= BC.
中位线定义:连接三角形两边中点的线段叫做三角形的中位线.
中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
1.如图,在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么当BC=____cm,CD=____cm时,四边形ABCD为平行四边形;
(2)若AC=10cm,BD=8cm,那么当AO=___cm,DO=___cm时,四边形ABCD为平行四边形.
2、下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.∠A=∠C,∠B=∠D
B.∠A=∠B=∠C=90 °
C.∠A+∠B=180°,∠B+∠C=180 °
D.∠A+∠B=180 °,∠C+∠D=180 °
A
B
C
D
D
3、下列条件中能判定一个四边形是平行四边形的条件是( )
①一组对边相等,且一组对角相等;
②一组对边相等且一条对角线平分另一条对角线;
③一组对角相等,且这一组对角的顶点所连结的对角线被另一条对角线平分;
④一组对角相等,且这一组对角的顶点所连结的对角线平分这组对角.
A.①和②
B.②和③
C.②和④
D.只有④
D
A
B
C
D
4、如图,在平行四边形ABCD的一组对边AD、BC上截取EF=MN,连接EM、FN,EM和FN有怎样的关系?为什么?
B
D
A
C
M
N
E
F
5.如图,点D、E、F分别是△ABC的边AB、BC、CA的中点,以这些点为顶点,你能在图中画出多少个平行四边形?
B
A
F
E
D
C
6.如图, A 、B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样测出A、B两点的实际距离?根据是什么?
A
B
C
小结
1、今天我们学行四边形的判定定理
2、三角形中位线的定义
3、三角形中位线定理
判定 文字语言 图形语言 符号语言
定义 两组对边分别平行的四边形是平行四边形
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
定理1 一组对边平行且相等的四边形是平行四边形 ∵AB=CD, AB∥CD,
∴四边形ABCD是平行四边形
定理2 两组对边分别相等的四边形是平等四边形
∵AB=CD,AD= BC ∴ 四边形ABCD是平行四边形
定理 3 对角线互相平分的四边形是平行四边形
∵OA=OC,OB=OD ∴四边形ABCD是平行四边形
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
O
学而不思则罔,思而不学则殆。
——孔子
