2021-2022学年度沪科版八年级数学下册课件 19.3 矩形 菱形 正方形(第1课时)(共16张PPT)
文档属性
| 名称 | 2021-2022学年度沪科版八年级数学下册课件 19.3 矩形 菱形 正方形(第1课时)(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 411.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览


文档简介
(共16张PPT)
19.3 矩形 菱形 正方形
引言
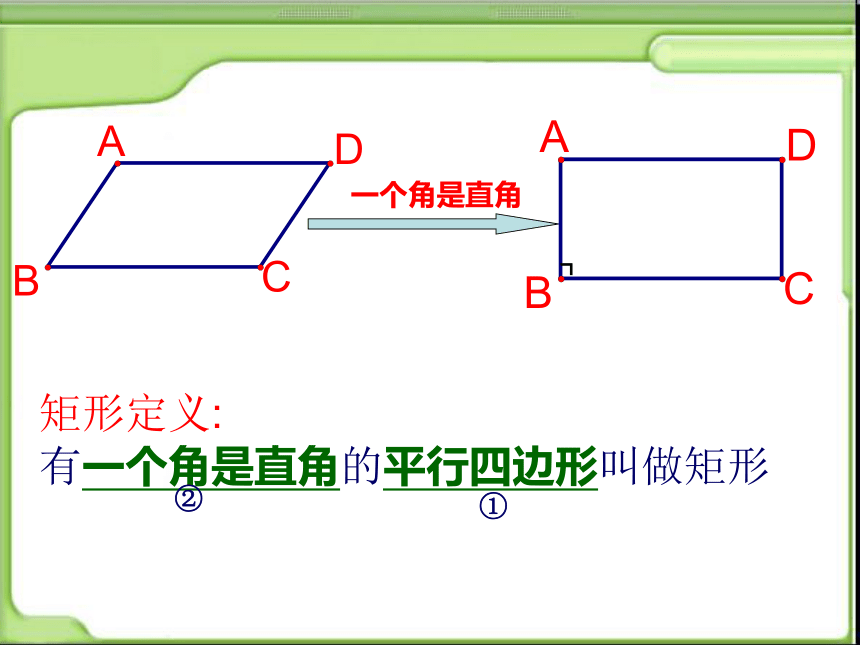
一个角是直角
┓
矩形定义:
有一个角是直角的平行四边形叫做矩形
①
②
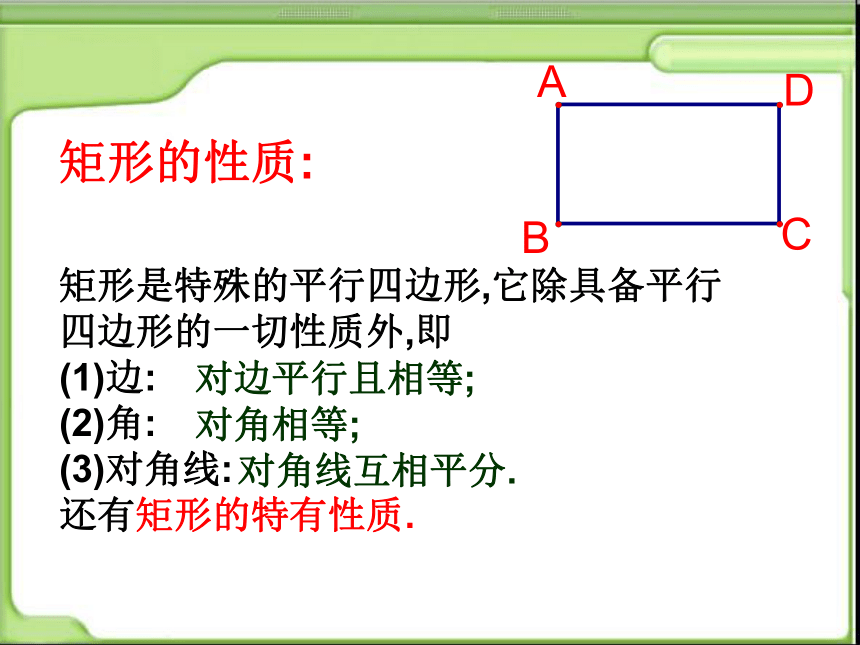
矩形的性质:
矩形是特殊的平行四边形,它除具备平行四边形的一切性质外,即
(1)边:
(2)角:
(3)对角线:
还有矩形的特有性质.
对边平行且相等;
对角相等;
对角线互相平分.
┓
矩形的四个角都是直角
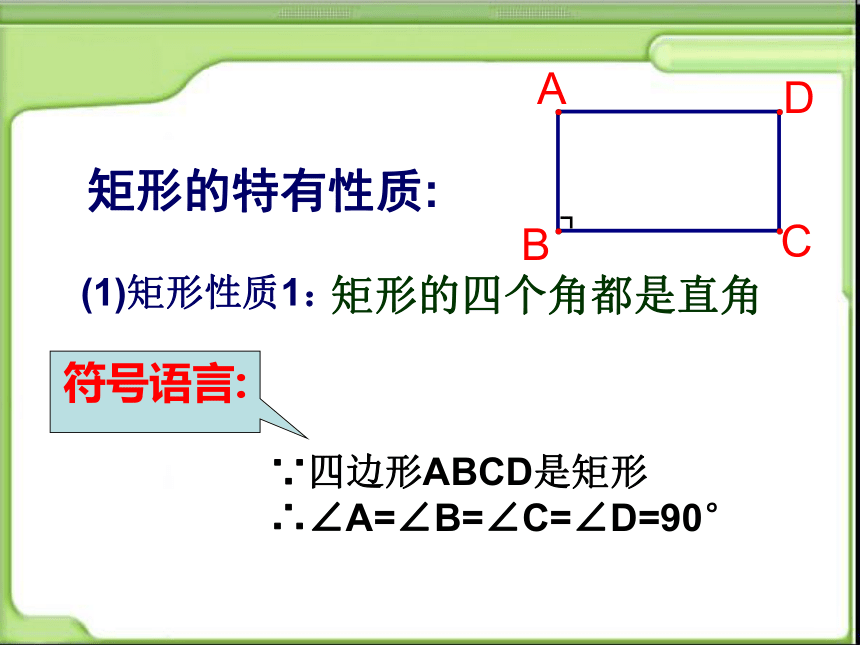
矩形的特有性质:
(1)矩形性质1:
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=90°
符号语言:
┓
┏
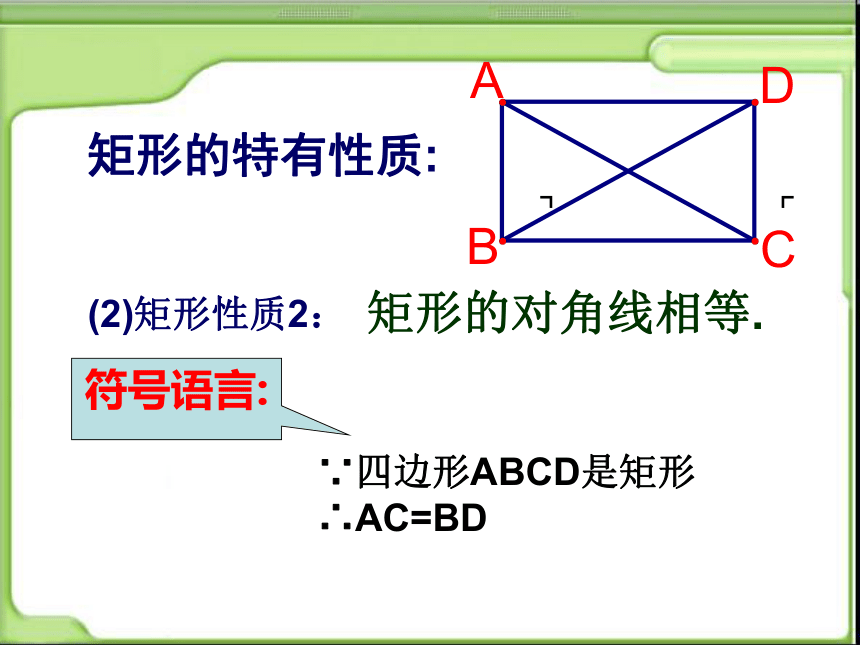
矩形的对角线相等.
(2)矩形性质2:
符号语言:
∵四边形ABCD是矩形
∴AC=BD
矩形的特有性质:
A
B
C
D
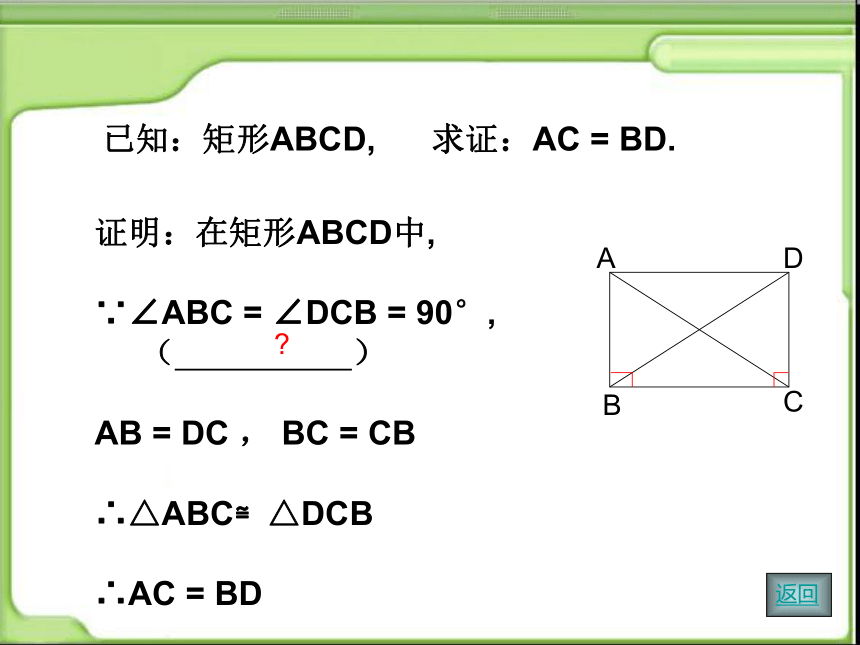
已知:矩形ABCD, 求证:AC = BD.
证明:在矩形ABCD中,
∵∠ABC = ∠DCB = 90°,
( )
AB = DC , BC = CB
∴△ABC≌△DCB
∴AC = BD
返回
又∵0A=0C= AC,
OB=OD= BD,
矩形性质2 矩形的对角线相等
∵四边形ABCD是矩形,
∴AC=BD.
∴OA=OB=OC=OD.
结论:
直角三角形斜边上的中线等于斜边的一半
归纳:
直角三角形的性质:
(1)直角三角形的两个锐角互余.
(2)直角三角形两条直角边的平方和等于斜边的平方.
(3)直角三角形斜边上的中线等于斜边的一半.
例1 已知:如图,矩形ABCD的两条对角线相交于点O, ∠AOB=60°,AB=4cm,求矩形对角线AC的长.
解:因为四边形ABCD是矩形,
所以AC=BD.
所以OA=OB.
因为∠AOB=120°,
所以∠OAB= ∠OBA
=(180°- 120°)÷2
=30°.
在Rt△ABD中,有
BD=2AD=2×4=8(cm).
理由是什么?
O
D
C
B
A
2.已知矩形的一条对角线长是8cm,两条对角线的一个交角为60°,则矩形的边长为______________
巩固练习:
1.在矩形ABCD中,∠AOD=130°,则∠ACB=___
25°
3.矩形ABCD中,AP⊥BD于P,BP:PD=1:3,
且AC、BD相交于点O,则∠AOB的度数
是_______.
┓
60°
4.已知:如图,在矩形ABCD中, 对角线相交于
点O,∠AOB=60°,AE平分∠BAC,AE交BC
于E,求∠BOE的度数.
O
D
C
B
A
E
30°
A:四边形集合
C:平行四边形集合
B:矩形集合
A
C
B
课堂小结
两组对边
分别平行
一个角是
直角
平行
四边形
矩形
返回
矩形的定义及性质
一个角是直角
定义:有一个角是直角的平行四边形叫做矩形
矩形
平行四边形
性质定理1 矩形的四个角都是直角
性质定理2 矩形的对角线相等★
矩形性质 角 边 对角线 对称性
推论:直角三角形斜边上的中线等于斜边的一半★
例1
练习
小结
四个角都
是直角
对边平行
且相等
互相平分
且相等
是轴对称
图形
学而不思则罔,思而不学则殆。
——孔子
19.3 矩形 菱形 正方形
引言
一个角是直角
┓
矩形定义:
有一个角是直角的平行四边形叫做矩形
①
②
矩形的性质:
矩形是特殊的平行四边形,它除具备平行四边形的一切性质外,即
(1)边:
(2)角:
(3)对角线:
还有矩形的特有性质.
对边平行且相等;
对角相等;
对角线互相平分.
┓
矩形的四个角都是直角
矩形的特有性质:
(1)矩形性质1:
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=90°
符号语言:
┓
┏
矩形的对角线相等.
(2)矩形性质2:
符号语言:
∵四边形ABCD是矩形
∴AC=BD
矩形的特有性质:
A
B
C
D
已知:矩形ABCD, 求证:AC = BD.
证明:在矩形ABCD中,
∵∠ABC = ∠DCB = 90°,
( )
AB = DC , BC = CB
∴△ABC≌△DCB
∴AC = BD
返回
又∵0A=0C= AC,
OB=OD= BD,
矩形性质2 矩形的对角线相等
∵四边形ABCD是矩形,
∴AC=BD.
∴OA=OB=OC=OD.
结论:
直角三角形斜边上的中线等于斜边的一半
归纳:
直角三角形的性质:
(1)直角三角形的两个锐角互余.
(2)直角三角形两条直角边的平方和等于斜边的平方.
(3)直角三角形斜边上的中线等于斜边的一半.
例1 已知:如图,矩形ABCD的两条对角线相交于点O, ∠AOB=60°,AB=4cm,求矩形对角线AC的长.
解:因为四边形ABCD是矩形,
所以AC=BD.
所以OA=OB.
因为∠AOB=120°,
所以∠OAB= ∠OBA
=(180°- 120°)÷2
=30°.
在Rt△ABD中,有
BD=2AD=2×4=8(cm).
理由是什么?
O
D
C
B
A
2.已知矩形的一条对角线长是8cm,两条对角线的一个交角为60°,则矩形的边长为______________
巩固练习:
1.在矩形ABCD中,∠AOD=130°,则∠ACB=___
25°
3.矩形ABCD中,AP⊥BD于P,BP:PD=1:3,
且AC、BD相交于点O,则∠AOB的度数
是_______.
┓
60°
4.已知:如图,在矩形ABCD中, 对角线相交于
点O,∠AOB=60°,AE平分∠BAC,AE交BC
于E,求∠BOE的度数.
O
D
C
B
A
E
30°
A:四边形集合
C:平行四边形集合
B:矩形集合
A
C
B
课堂小结
两组对边
分别平行
一个角是
直角
平行
四边形
矩形
返回
矩形的定义及性质
一个角是直角
定义:有一个角是直角的平行四边形叫做矩形
矩形
平行四边形
性质定理1 矩形的四个角都是直角
性质定理2 矩形的对角线相等★
矩形性质 角 边 对角线 对称性
推论:直角三角形斜边上的中线等于斜边的一半★
例1
练习
小结
四个角都
是直角
对边平行
且相等
互相平分
且相等
是轴对称
图形
学而不思则罔,思而不学则殆。
——孔子
