2021-2022学年度沪科版八年级数学下册课件 20.2数据的集中趋势和离散程度(第1课时)(共17张PPT)
文档属性
| 名称 | 2021-2022学年度沪科版八年级数学下册课件 20.2数据的集中趋势和离散程度(第1课时)(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
20.2 数据的集中趋势和离散程度
(第1课时)
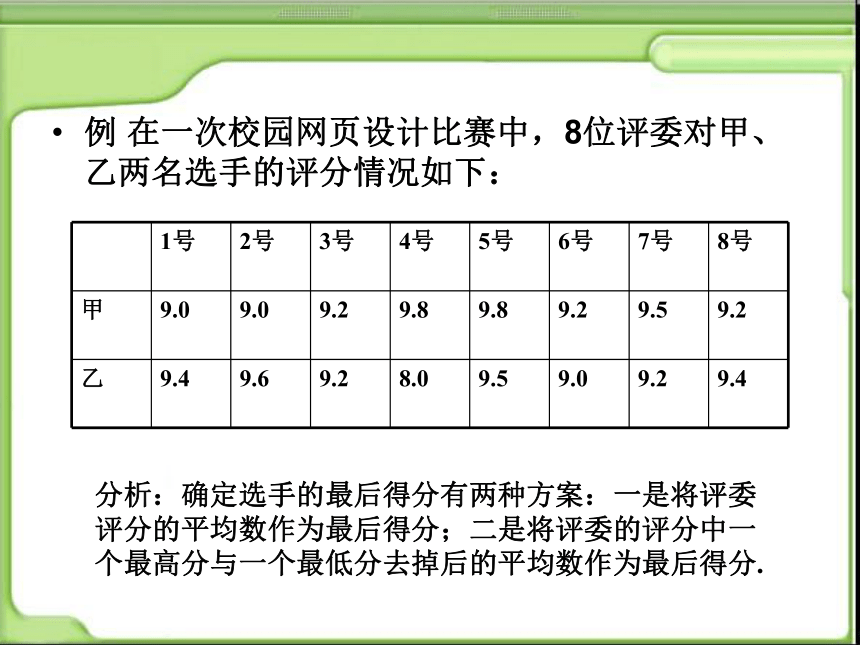
例 在一次校园网页设计比赛中,8位评委对甲、乙两名选手的评分情况如下:
1号 2号 3号 4号 5号 6号 7号 8号
甲 9.0 9.0 9.2 9.8 9.8 9.2 9.5 9.2
乙 9.4 9.6 9.2 8.0 9.5 9.0 9.2 9.4
分析:确定选手的最后得分有两种方案:一是将评委评分的平均数作为最后得分;二是将评委的评分中一个最高分与一个最低分去掉后的平均数作为最后得分.
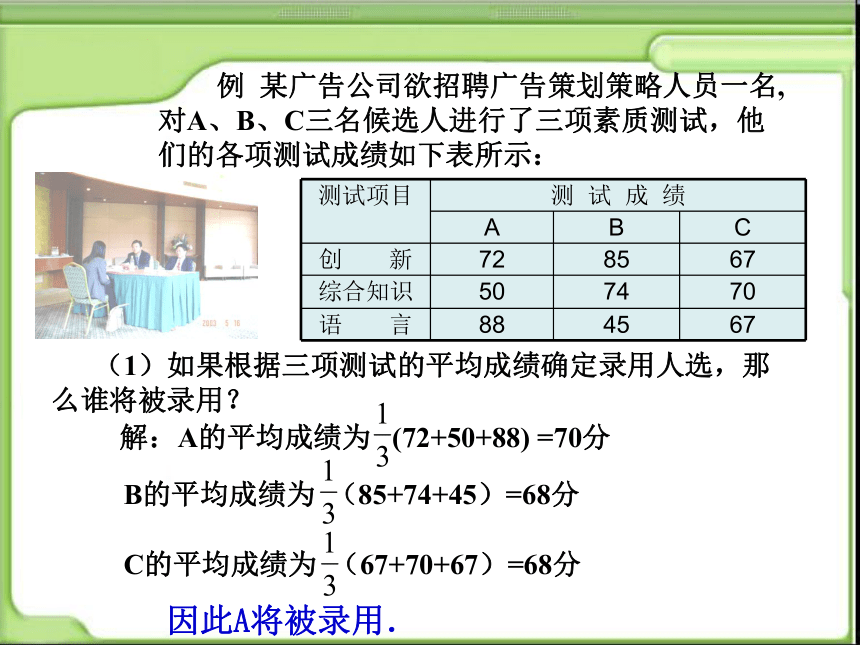
例 某广告公司欲招聘广告策划策略人员一名,对A、B、C三名候选人进行了三项素质测试,他们的各项测试成绩如下表所示:
测试项目 测 试 成 绩
A B C
创 新 72 85 67
综合知识 50 74 70
语 言 88 45 67
(1)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用?
因此A将被录用.
解:A的平均成绩为 (72+50+88) =70分
B的平均成绩为 (85+74+45)=68分
C的平均成绩为 (67+70+67)=68分
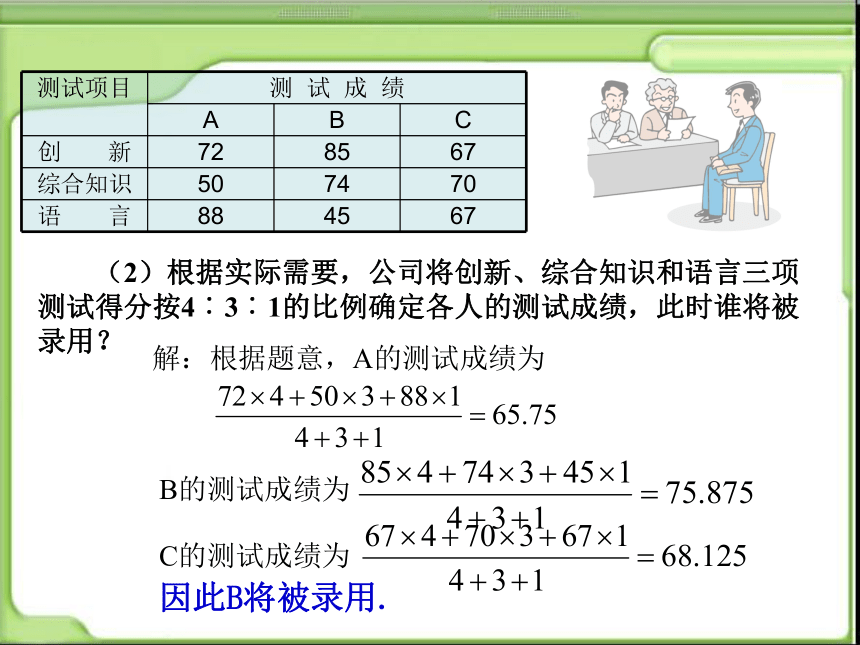
测试项目 测 试 成 绩
A B C
创 新 72 85 67
综合知识 50 74 70
语 言 88 45 67
(2)根据实际需要,公司将创新、综合知识和语言三项测试得分按4︰3︰1的比例确定各人的测试成绩,此时谁将被录用?
因此B将被录用.
解:根据题意,A的测试成绩为
B的测试成绩为
C的测试成绩为
不同的运算录取的结果不一样说明了什么?
实际问题中,一组数据的各个数据的“重要程度”未必相同。因此,在计算这组数据的平均数时,往往给每个数据一个“权”,如例题中4,3,1分别是创新、综合知识、语言三项测试成绩的权,而称
为A的三项测试成绩的加权平均数.
数据的权能够反映数据的相对“重要程度”。
加
权
平
均
数
练一练:
1.某班10名学生为支援“希望工程”将平时积攒的零花钱捐献给贫困地区的失学儿童,每人捐款金额如下(单位:元):
10, 12, 13.5, 21, 40.8, 19.5, 20.8, 25, 16, 30
这10名同学平均捐款多少元
解:这10名同学的平均捐款为
(10+12+13.5+21+40.8+19.5+20.8+25
+16+30) ÷10=20.86(元)
答:这10名同学平均捐款20.86元
2、请你求下面这组数据的平均数:
105 103 101 100 101 114 108 106 110 98
3、从一批机器零件毛坯中取出20件,称得它们的质量如下:(单位:g)
208 200 205 202 218 206 214 215 207 207 218 192 202 216 185 227 187 215
试求这批零件质量的平均数.
4、某公司欲招聘公关人员,对甲、乙候选人进行了面视和笔试,他们的成绩如下表所示:
(1)如果公司认为面试和笔试同等重要,从他们的成绩看,谁将被录取?
候选人 测试成绩(百分制)
测试 笔试
甲 86 90
乙 92 83
(2)如果公司认为,作为公关人员面试的成绩应该比笔试更重要,并分别赋予它们6和4的权,计算甲、两人各自的平均成绩,看看谁将被录取?
考考你:有一篇报道说,有一个身高1.7米的人在平均水深只有0.5米的一条河流中淹死了,你感觉奇怪吗?
请你来做教练:
为了从甲乙两名学生中选拔一人参加射击比赛,对他们的射击水平进行了测验.两人在相同条件下各射靶10次,命中的环数如下:
甲 7 8 6 8 6 5 9 10 7 4
乙 9 5 7 8 7 6 8 6 7 7
请问:你选哪一个人参加射击比赛?
总 结
再见!
课后要好好总结哦!
学而不思则罔,思而不学则殆。
——孔子
20.2 数据的集中趋势和离散程度
(第1课时)
例 在一次校园网页设计比赛中,8位评委对甲、乙两名选手的评分情况如下:
1号 2号 3号 4号 5号 6号 7号 8号
甲 9.0 9.0 9.2 9.8 9.8 9.2 9.5 9.2
乙 9.4 9.6 9.2 8.0 9.5 9.0 9.2 9.4
分析:确定选手的最后得分有两种方案:一是将评委评分的平均数作为最后得分;二是将评委的评分中一个最高分与一个最低分去掉后的平均数作为最后得分.
例 某广告公司欲招聘广告策划策略人员一名,对A、B、C三名候选人进行了三项素质测试,他们的各项测试成绩如下表所示:
测试项目 测 试 成 绩
A B C
创 新 72 85 67
综合知识 50 74 70
语 言 88 45 67
(1)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用?
因此A将被录用.
解:A的平均成绩为 (72+50+88) =70分
B的平均成绩为 (85+74+45)=68分
C的平均成绩为 (67+70+67)=68分
测试项目 测 试 成 绩
A B C
创 新 72 85 67
综合知识 50 74 70
语 言 88 45 67
(2)根据实际需要,公司将创新、综合知识和语言三项测试得分按4︰3︰1的比例确定各人的测试成绩,此时谁将被录用?
因此B将被录用.
解:根据题意,A的测试成绩为
B的测试成绩为
C的测试成绩为
不同的运算录取的结果不一样说明了什么?
实际问题中,一组数据的各个数据的“重要程度”未必相同。因此,在计算这组数据的平均数时,往往给每个数据一个“权”,如例题中4,3,1分别是创新、综合知识、语言三项测试成绩的权,而称
为A的三项测试成绩的加权平均数.
数据的权能够反映数据的相对“重要程度”。
加
权
平
均
数
练一练:
1.某班10名学生为支援“希望工程”将平时积攒的零花钱捐献给贫困地区的失学儿童,每人捐款金额如下(单位:元):
10, 12, 13.5, 21, 40.8, 19.5, 20.8, 25, 16, 30
这10名同学平均捐款多少元
解:这10名同学的平均捐款为
(10+12+13.5+21+40.8+19.5+20.8+25
+16+30) ÷10=20.86(元)
答:这10名同学平均捐款20.86元
2、请你求下面这组数据的平均数:
105 103 101 100 101 114 108 106 110 98
3、从一批机器零件毛坯中取出20件,称得它们的质量如下:(单位:g)
208 200 205 202 218 206 214 215 207 207 218 192 202 216 185 227 187 215
试求这批零件质量的平均数.
4、某公司欲招聘公关人员,对甲、乙候选人进行了面视和笔试,他们的成绩如下表所示:
(1)如果公司认为面试和笔试同等重要,从他们的成绩看,谁将被录取?
候选人 测试成绩(百分制)
测试 笔试
甲 86 90
乙 92 83
(2)如果公司认为,作为公关人员面试的成绩应该比笔试更重要,并分别赋予它们6和4的权,计算甲、两人各自的平均成绩,看看谁将被录取?
考考你:有一篇报道说,有一个身高1.7米的人在平均水深只有0.5米的一条河流中淹死了,你感觉奇怪吗?
请你来做教练:
为了从甲乙两名学生中选拔一人参加射击比赛,对他们的射击水平进行了测验.两人在相同条件下各射靶10次,命中的环数如下:
甲 7 8 6 8 6 5 9 10 7 4
乙 9 5 7 8 7 6 8 6 7 7
请问:你选哪一个人参加射击比赛?
总 结
再见!
课后要好好总结哦!
学而不思则罔,思而不学则殆。
——孔子
