人教版(2019)高中物理 必修第二册6.1 圆周运动学案(word含答案)
文档属性
| 名称 | 人教版(2019)高中物理 必修第二册6.1 圆周运动学案(word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-11-25 00:00:00 | ||
图片预览



文档简介
1.圆周运动
(1)认识圆周运动、匀速圆周运动的特点,了解描述圆周运动快慢的基本思路,了解转速和周期的意义. (2)理解线速度的物理意义,知道匀速圆周运动中线速度的方向. (3)理解角速度的物理意义,掌握线速度和角速度的关系. (4)能在具体的情境中确定线速度和角速度.
必备知识·自主学习——突出基础性 素养夯基
一、线速度
1.大小:Δt非常非常小时,弧长Δs与时间的比值称为线速度(linear velocity).
2.定义式:________.
3.意义:描述做圆周运动的物体运动的快慢.
4.方向:线速度是矢量,线速度的方向为物体做圆周运动时该点的切线方向.
5.匀速圆周运动
(1)定义:物体沿着圆周运动,并且线速度的大小________的运动.这种运动叫作匀速圆周运动(uniform circular motion).
(2)性质:线速度的方向是时刻________的,所以是一种________运动.
举例:生活中的圆周运动
二、角速度
1.定义:物体在Δt时间内由A运动到B.半径OA在这段时间内转过的角Δθ与所用时间Δt之比叫作角速度(angular velocity).
2.定义式:ω=
3.单位:在SI制中,弧度每秒,符号是________.在运算中, 通常把“弧度”或“rad”略去不写,所以角速度的单位可以写为s-1.
4.物理意义:用来描述物体绕圆心转动快慢的物理量.
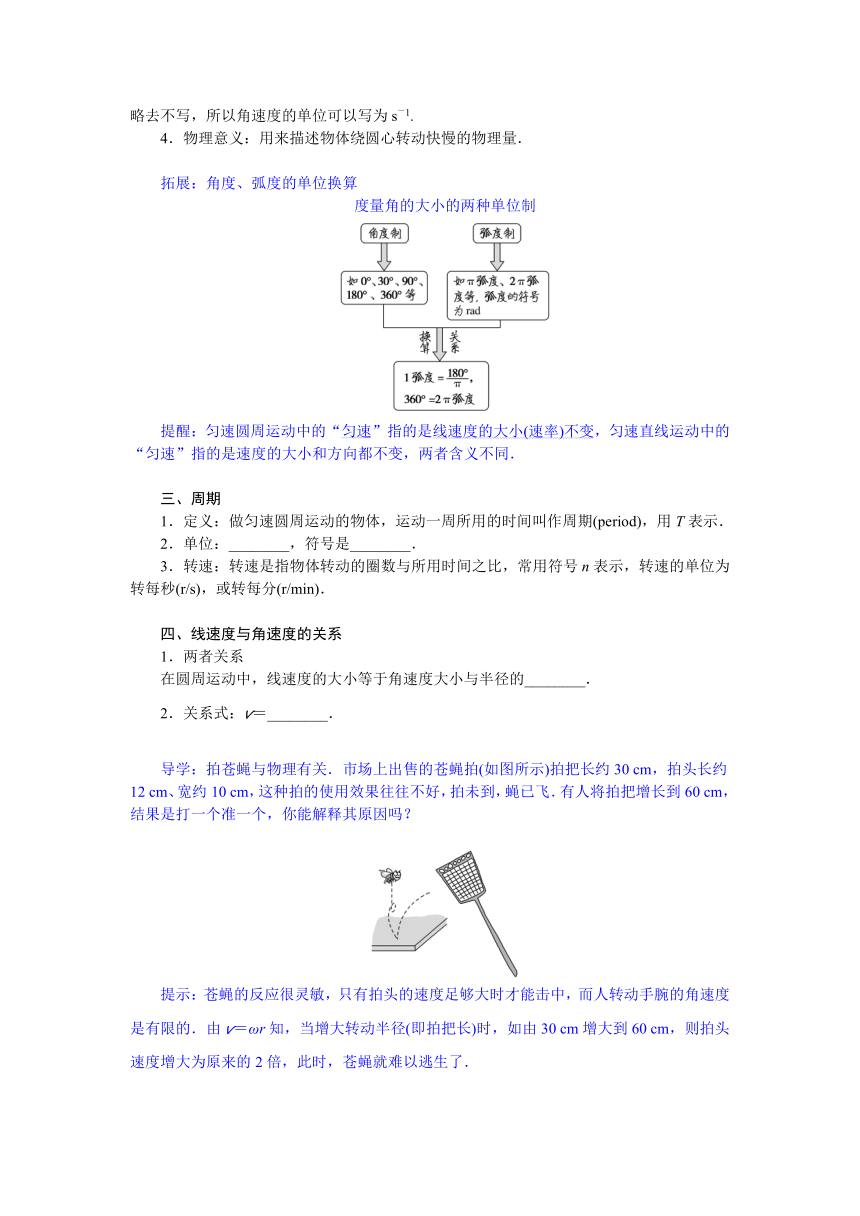
拓展:角度、弧度的单位换算
度量角的大小的两种单位制
提醒:匀速圆周运动中的“匀速”指的是线速度的大小(速率)不变,匀速直线运动中的“匀速”指的是速度的大小和方向都不变,两者含义不同.
三、周期
1.定义:做匀速圆周运动的物体,运动一周所用的时间叫作周期(period),用T表示.
2.单位:________,符号是________.
3.转速:转速是指物体转动的圈数与所用时间之比,常用符号n表示,转速的单位为转每秒(r/s),或转每分(r/min).
四、线速度与角速度的关系
1.两者关系
在圆周运动中,线速度的大小等于角速度大小与半径的________.
2.关系式:v=________.
导学:拍苍蝇与物理有关.市场上出售的苍蝇拍(如图所示)拍把长约30 cm,拍头长约12 cm、宽约10 cm,这种拍的使用效果往往不好,拍未到,蝇已飞.有人将拍把增长到60 cm,结果是打一个准一个,你能解释其原因吗?
提示:苍蝇的反应很灵敏,只有拍头的速度足够大时才能击中,而人转动手腕的角速度是有限的.由v=ωr知,当增大转动半径(即拍把长)时,如由30 cm增大到60 cm,则拍头速度增大为原来的2倍,此时,苍蝇就难以逃生了.
【思考辨析】 判断正误,正确的画“√”,错误的画“×”.
(1)匀速圆周运动是一种匀速运动.( )
(2)做匀速圆周运动的物体,相等时间内通过的位移相同.( )
(3)做匀速圆周运动的物体,其所受合力一定不为零.( )
(4)在描述圆周运动的物理量中,线速度是矢量,周期、转速是标量.( )
(5)做圆周运动的物体转过的角度越大,其角速度就越大.( )
(6)当半径一定时,线速度和角速度成正比.( )
关键能力·合作探究——突出综合性 素养形成
探究点一 描述圆周运动的物理量
导学探究
闹钟与手表为什么会有上述快慢之争?提出你的看法,和同学进行讨论.
探究总结
1.描述圆周运动的物理量
(1)线速度:单位时间(1 s内)转过的弧长.
(2)角速度:单位时间(1 s内)转过的圆心角.
(3)周期:转一圈所用的时间.
(4)频率(转速):单位时间内转过的圈数.
2.描述圆周运动的各物理量之间的关系:
(1)v===2πnr
(2)ω===2πn
(3)v=ωr
3.各物理量之间关系的分析技巧:
(1)角速度、周期、转速之间关系的理解:物体做匀速圆周运动时,由ω==2πn知,角速度、周期、转速三个物理量,只要其中一个物理量确定了,其余两个物理量也唯一确定了.
(2)线速度与角速度之间的关系理解:由v=ωr知,r一定时,v∝ω;v一定时,ω∝;ω一定时,v∝r.
典例示范
题型一 线速度的理解与计算
【例1】 (多选)某同学参加了糕点制作的选修课,在绕中心匀速转动的圆盘上放了一块直径约25 cm的蛋糕(圆盘与蛋糕中心重合).他要在蛋糕上均匀“点”上奶油,挤奶油时手处于圆盘上方静止不动,奶油竖直下落到蛋糕表面,若不计奶油下落时间,每隔2 s“点”一次奶油,蛋糕一周均匀“点”上10个奶油.下列说法正确的是( )
A.圆盘转动一周历时18 s
B.圆盘转动一周历时20 s
C.蛋糕边缘的奶油(可视为质点)线速度大小约为 m/s
D.蛋糕边缘的奶油(可视为质点)线速度大小约为 m/s
题型二 角速度的理解与计算
【例2】 某品牌的机械鼠标内部结构如图所示,机械鼠标中的定位球的直径是2.0 cm,某次操作中将鼠标沿直线匀速移动12 cm需要的时间为1 s,则定位球的角速度为( )
A. rad/s B. rad/s
C.6 rad/s D.12 rad/s
题型三 描述圆周运动的几个物理量间的关系
【例3】 (多选)质点做匀速圆周运动时,以下说法中正确的是( )
A.线速度越大,其角速度也一定越大
B.角速度越大,其转速也一定越大
C.线速度一定时,半径越大则周期越长
D.角速度一定时,半径越大则周期越长
练1 (多选)一质点做匀速圆周运动,其线速度大小为4 m/s,转动周期为2 s,则下列说法正确的( )
A.角速度为0.5 rad/s
B.转速为0.5 r/s
C.运动轨迹的半径约为1.27 m
D.频率为0.5 Hz
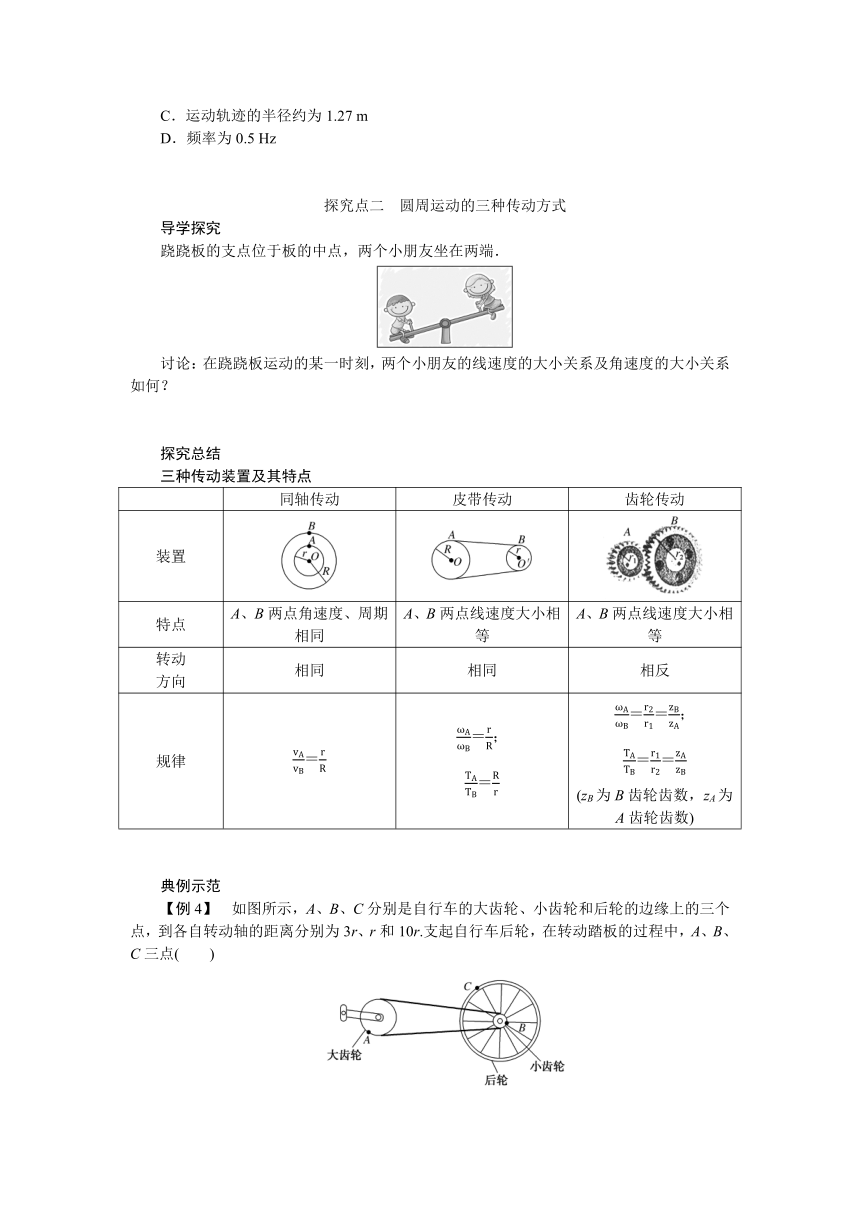
探究点二 圆周运动的三种传动方式
导学探究
跷跷板的支点位于板的中点,两个小朋友坐在两端.
讨论:在跷跷板运动的某一时刻,两个小朋友的线速度的大小关系及角速度的大小关系如何?
探究总结
三种传动装置及其特点
同轴传动 皮带传动 齿轮传动
装置
特点 A、B两点角速度、周期相同 A、B两点线速度大小相等 A、B两点线速度大小相等
转动 方向 相同 相同 相反
规律 = =; = ==; == (zB为B齿轮齿数,zA为A齿轮齿数)
典例示范
【例4】 如图所示,A、B、C分别是自行车的大齿轮、小齿轮和后轮的边缘上的三个点,到各自转动轴的距离分别为3r、r和10r.支起自行车后轮,在转动踏板的过程中,A、B、C三点( )
A.角速度大小关系是ωA>ωB=ωC
B.线速度大小关系是vAC.转动周期之比TA∶TB∶TC=3∶1∶1
D.转速之比nA∶nB∶nC=3∶3∶1
练2 如图所示,地球可以看作一个球体,O点为地球球心,位于长沙的物体A和位于赤道上的物体B,都随地球自转做匀速圆周运动,则( )
A.物体的周期TA=TB
B.物体的周期TA>TB
C.物体的线速度大小vA>vB
D.物体的角速度大小ωA<ωB
练3 在汽车无极变速器中,存在如图所示的装置,A是与B同轴相连的齿轮,C是与D同轴相连的齿轮,A、C、M为相互咬合的齿轮.已知齿轮A、C规格相同,半径为R,齿轮B、D规格也相同,半径为1.5R,齿轮M的半径为0.9R.当齿轮M如图方向转动时以下说法正确的是( )
A.齿轮D和齿轮B的转动方向相反
B.齿轮D和齿轮B的转动周期之比为1∶1
C.齿轮M和齿轮B边缘某点的线速度大小之比为1∶1
D.齿轮M和齿轮C的角速度大小之比为9∶10
解答传动问题要“三看、一记、二明确”
(1)三看:一看题,看题目说明的情境;二看图,看图片是同轴传动还是皮带传动;三看联系,看内部结构的各个组成部分之间是什么关系,即靠齿轮、皮带、摩擦等.
(2)一记:一记是指记公式,公式有v=ωr、T=以及v=rω==2πrn等.
(3)二明确:①在通常情况下,同轴传动的各点角速度ω、转速n和周期T相等,线速度v=ωr,即与半径成正比.②在认为皮带不打滑的情况下,传动皮带和与皮带连接的轮边缘上各点的线速度大小相等,由ω=可知,角速度与半径成反比.
随堂演练·达标自测——突出创新性 素养达标
1.关于做匀速圆周运动的物体的线速度、角速度、周期的关系,下列说法中正确的是 ( )
A.线速度大的角速度一定大
B.线速度大的周期一定小
C.角速度大的运动半径一定小
D.角速度大的周期一定小
2.一户外健身器材如图所示.当器材上轮子转动时,轮子上A、B两点的( )
A.转速nB>nA
B.周期TB>TA
C.线速度vB>vA
D.角速度ωB>ωA
3.(多选)明代出版的《天工开物》一书中就有牛力齿轮翻车的图画(如图所示),记录了我们祖先的劳动智慧.若A、B两齿轮的半径关系为rA>rB,则( )
A.齿轮A、B的角速度大小相等
B.齿轮A的角速度大小小于齿轮B的角速度大小
C.齿轮A、B边缘的线速度大小相等
D.齿轮A边缘的线速度大小小于齿轮B边缘的线速度大小
4.(多选)如图所示是中国古代玩具饮水鸟的示意图,它的神奇之处是,在鸟的面前放上一杯水,鸟就会俯下身去,把嘴浸到水里,“喝”了一口水后,鸟将绕着O点不停摆动,一会儿它又会俯下身去,再“喝”一口水.P、Q是饮水鸟上两点,且rPO>rQO,则在摆动过程中( )
A.P点的线速度小于Q点的线速度
B.P、Q两点的角速度大小相等
C.相同时间内P、Q两点通过的弧长相等
D.P、Q两点的线速度方向相反
5.火车以15 m/s的速率转过一段弯道,某乘客发现放在桌面上的指南针在10 s内匀速转过了约10°.在此10 s时间内,下列对火车的说法正确的是 ( )
A.运动路程为150 m B.加速度为零
C.角速度约为1 rad/s D.周期约为60 s
1.圆周运动
必备知识·自主学习
一、
2.v=
5.(1)处处相等 (2)变化 变速
二、
3.rad/s
三、
2.秒 s
四、
1.乘积
2.ωr
思考辨析
答案:(1)× (2)× (3)√ (4)√ (5)× (6)√
关键能力·合作探究
探究点一
提示:闹钟和手表是从不同角度看圆周运动的:闹钟指的是秒针针尖的线速度;手表则指的是描述秒针运动的另一个物理量,这个物理量就是角速度.
【例1】 【解析】 每隔2 s“点”一次奶油,蛋糕一周均匀“点”上10个奶油,则圆盘转动一圈的时间T=20 s,A错误,B正确;蛋糕边缘的奶油(可视为质点)线速度大小约为v=== m/s= m/s,C正确,D错误.
【答案】 BC
【例2】 【解析】 根据线速度定义式有v=,定位球的线速度为v= cm/s=12 cm/s,角速度与线速度关系为v=ωr,因此定位球的角速度为ω== rad/s=12 rad/s,选项D正确.
【答案】 D
【例3】 【解析】 由v=ωr知,当半径一定时,线速度越大,角速度越大,A错误;由ω=2nπ知,角速度越大,转速越大,B正确;由v=知,线速度一定时,半径越大,周期越长,C正确;由ω=知,角速度一定时,周期一定,与半径无关,D错误.
【答案】 BC
练1 解析:由题意知v=4 m/s,T=2 s,根据角速度与周期的关系可知ω==π rad/s.由线速度与角速度的关系v=ωr得r== m≈1.27 m.由v=2πnr得转速n==0.5 r/s.由频率与周期的关系得f==0.5 Hz,故选项A错误,B、C、D正确.
答案:BCD
探究点二
提示:线速度的大小和角速度的大小都相同.
【例4】 【解析】 大齿轮与小齿轮是链条传动,边缘点线速度相等,则有vA∶vB=1∶1,根据v=ωr,则有ωA∶ωB=rB∶rA=1∶3;小齿轮与后轮是同轴传动,角速度相等,则有ωB∶ωC=1∶1,根据v=ωr,则有vB∶vC=1∶10,所以角速度大小关系是ωA∶ωB∶ωC=1∶3∶3,线速度大小关系是vA∶vB∶vC=1∶1∶10,根据T=,可知TA∶TB∶TC=3∶1∶1,根据ω=2πn可知,转速之比是nA∶nB∶nC=1∶3∶3,故选项C正确.
【答案】 C
练2 解析:A对,B、D错:两物体随地球自转,同轴传动,所以角速度ω相同,根据ω=可知两物体周期相同,即ωA=ωB,TA=TB.C错:物体做圆周运动的半径由物体指向地轴,根据题图可知rA答案:A
练3 解析:A错:A、M、C三个紧密咬合的齿轮是同缘传动,因为M顺时针转动,故A逆时针转动,C逆时针转动,又A、B同轴传动,C、D同轴传动,所以齿轮D和齿轮B的转动方向相同.B对:A、M、C三个紧密咬合的齿轮是同缘传动,边缘线速度大小相同,齿轮A、C规格相同,半径为R,根据v=ωr得,A、C转动的角速度相同,A、B同轴传动,角速度相同,C、D同轴传动,角速度相同,且齿轮B、D规格也相同,所以齿轮D和齿轮B的转动周期相同.C错:A、M、C三个紧密咬合的齿轮是同缘传动,边缘线速度大小相同;A与B属于同轴传动,角速度相等,由于B的半径大于A的半径,所以B边缘的线速度大于A边缘的线速度,所以B边缘的线速度也大于M边缘的线速度.D错:A、M、C三个紧密咬合的齿轮是同缘传动,边缘线速度大小相同,根据v=ωr得:===.
答案:B
随堂演练·达标自测
1.解析:由v=ωr知,r一定时,v与ω成正比;v一定时,ω与r成反比,故A、C错误.由v=知,r一定时,v越大,T越小,故B错误.由ω=可知,ω越大,T越小,故D正确.
答案:D
2.答案:C
3.解析:齿轮A、B为齿轮传动,齿轮A、B边缘的线速度大小相等,且齿轮A的半径比齿轮B的大,根据v=ωr可知齿轮A的角速度大小小于齿轮B的角速度大小,A、D错误,B、C正确.
答案:BC
4.解析:鸟将绕着O点不停摆动,P、Q是饮水鸟上两点,属于同轴转动.P点离O点更远,绕O点转动的半径大.根据同轴转动角速度相等知P、Q两点的角速度大小相等,故B正确;P、Q两点的角速度大小相同,P点绕O点转动的半径大,根据v=ωr知,P点的线速度较大,故A错误;P、Q两点的线速度大小不同,故相同时间内通过的弧长不相等,故C错误;P、Q在O点两端,两点的线速度方向均与杆垂直,故两点的线速度方向相反,选项D正确.
答案:BD
5.解析:火车以15 m/s的速率转弯,可看成做匀速圆周运动,则在10 s内的路程为s=vt=150 m,A正确;火车做曲线运动,速度在不断变化,因此加速度一定不为零,B错误;指南针在10 s内匀速转过了约10°,又10°=×2π rad= rad,根据角速度的定义可得角速度约为ω= rad/s= rad/s,C错误;根据角速度与周期的关系可得周期为T=≈ s=360 s,D错误.
答案:A
(1)认识圆周运动、匀速圆周运动的特点,了解描述圆周运动快慢的基本思路,了解转速和周期的意义. (2)理解线速度的物理意义,知道匀速圆周运动中线速度的方向. (3)理解角速度的物理意义,掌握线速度和角速度的关系. (4)能在具体的情境中确定线速度和角速度.
必备知识·自主学习——突出基础性 素养夯基
一、线速度
1.大小:Δt非常非常小时,弧长Δs与时间的比值称为线速度(linear velocity).
2.定义式:________.
3.意义:描述做圆周运动的物体运动的快慢.
4.方向:线速度是矢量,线速度的方向为物体做圆周运动时该点的切线方向.
5.匀速圆周运动
(1)定义:物体沿着圆周运动,并且线速度的大小________的运动.这种运动叫作匀速圆周运动(uniform circular motion).
(2)性质:线速度的方向是时刻________的,所以是一种________运动.
举例:生活中的圆周运动
二、角速度
1.定义:物体在Δt时间内由A运动到B.半径OA在这段时间内转过的角Δθ与所用时间Δt之比叫作角速度(angular velocity).
2.定义式:ω=
3.单位:在SI制中,弧度每秒,符号是________.在运算中, 通常把“弧度”或“rad”略去不写,所以角速度的单位可以写为s-1.
4.物理意义:用来描述物体绕圆心转动快慢的物理量.
拓展:角度、弧度的单位换算
度量角的大小的两种单位制
提醒:匀速圆周运动中的“匀速”指的是线速度的大小(速率)不变,匀速直线运动中的“匀速”指的是速度的大小和方向都不变,两者含义不同.
三、周期
1.定义:做匀速圆周运动的物体,运动一周所用的时间叫作周期(period),用T表示.
2.单位:________,符号是________.
3.转速:转速是指物体转动的圈数与所用时间之比,常用符号n表示,转速的单位为转每秒(r/s),或转每分(r/min).
四、线速度与角速度的关系
1.两者关系
在圆周运动中,线速度的大小等于角速度大小与半径的________.
2.关系式:v=________.
导学:拍苍蝇与物理有关.市场上出售的苍蝇拍(如图所示)拍把长约30 cm,拍头长约12 cm、宽约10 cm,这种拍的使用效果往往不好,拍未到,蝇已飞.有人将拍把增长到60 cm,结果是打一个准一个,你能解释其原因吗?
提示:苍蝇的反应很灵敏,只有拍头的速度足够大时才能击中,而人转动手腕的角速度是有限的.由v=ωr知,当增大转动半径(即拍把长)时,如由30 cm增大到60 cm,则拍头速度增大为原来的2倍,此时,苍蝇就难以逃生了.
【思考辨析】 判断正误,正确的画“√”,错误的画“×”.
(1)匀速圆周运动是一种匀速运动.( )
(2)做匀速圆周运动的物体,相等时间内通过的位移相同.( )
(3)做匀速圆周运动的物体,其所受合力一定不为零.( )
(4)在描述圆周运动的物理量中,线速度是矢量,周期、转速是标量.( )
(5)做圆周运动的物体转过的角度越大,其角速度就越大.( )
(6)当半径一定时,线速度和角速度成正比.( )
关键能力·合作探究——突出综合性 素养形成
探究点一 描述圆周运动的物理量
导学探究
闹钟与手表为什么会有上述快慢之争?提出你的看法,和同学进行讨论.
探究总结
1.描述圆周运动的物理量
(1)线速度:单位时间(1 s内)转过的弧长.
(2)角速度:单位时间(1 s内)转过的圆心角.
(3)周期:转一圈所用的时间.
(4)频率(转速):单位时间内转过的圈数.
2.描述圆周运动的各物理量之间的关系:
(1)v===2πnr
(2)ω===2πn
(3)v=ωr
3.各物理量之间关系的分析技巧:
(1)角速度、周期、转速之间关系的理解:物体做匀速圆周运动时,由ω==2πn知,角速度、周期、转速三个物理量,只要其中一个物理量确定了,其余两个物理量也唯一确定了.
(2)线速度与角速度之间的关系理解:由v=ωr知,r一定时,v∝ω;v一定时,ω∝;ω一定时,v∝r.
典例示范
题型一 线速度的理解与计算
【例1】 (多选)某同学参加了糕点制作的选修课,在绕中心匀速转动的圆盘上放了一块直径约25 cm的蛋糕(圆盘与蛋糕中心重合).他要在蛋糕上均匀“点”上奶油,挤奶油时手处于圆盘上方静止不动,奶油竖直下落到蛋糕表面,若不计奶油下落时间,每隔2 s“点”一次奶油,蛋糕一周均匀“点”上10个奶油.下列说法正确的是( )
A.圆盘转动一周历时18 s
B.圆盘转动一周历时20 s
C.蛋糕边缘的奶油(可视为质点)线速度大小约为 m/s
D.蛋糕边缘的奶油(可视为质点)线速度大小约为 m/s
题型二 角速度的理解与计算
【例2】 某品牌的机械鼠标内部结构如图所示,机械鼠标中的定位球的直径是2.0 cm,某次操作中将鼠标沿直线匀速移动12 cm需要的时间为1 s,则定位球的角速度为( )
A. rad/s B. rad/s
C.6 rad/s D.12 rad/s
题型三 描述圆周运动的几个物理量间的关系
【例3】 (多选)质点做匀速圆周运动时,以下说法中正确的是( )
A.线速度越大,其角速度也一定越大
B.角速度越大,其转速也一定越大
C.线速度一定时,半径越大则周期越长
D.角速度一定时,半径越大则周期越长
练1 (多选)一质点做匀速圆周运动,其线速度大小为4 m/s,转动周期为2 s,则下列说法正确的( )
A.角速度为0.5 rad/s
B.转速为0.5 r/s
C.运动轨迹的半径约为1.27 m
D.频率为0.5 Hz
探究点二 圆周运动的三种传动方式
导学探究
跷跷板的支点位于板的中点,两个小朋友坐在两端.
讨论:在跷跷板运动的某一时刻,两个小朋友的线速度的大小关系及角速度的大小关系如何?
探究总结
三种传动装置及其特点
同轴传动 皮带传动 齿轮传动
装置
特点 A、B两点角速度、周期相同 A、B两点线速度大小相等 A、B两点线速度大小相等
转动 方向 相同 相同 相反
规律 = =; = ==; == (zB为B齿轮齿数,zA为A齿轮齿数)
典例示范
【例4】 如图所示,A、B、C分别是自行车的大齿轮、小齿轮和后轮的边缘上的三个点,到各自转动轴的距离分别为3r、r和10r.支起自行车后轮,在转动踏板的过程中,A、B、C三点( )
A.角速度大小关系是ωA>ωB=ωC
B.线速度大小关系是vA
D.转速之比nA∶nB∶nC=3∶3∶1
练2 如图所示,地球可以看作一个球体,O点为地球球心,位于长沙的物体A和位于赤道上的物体B,都随地球自转做匀速圆周运动,则( )
A.物体的周期TA=TB
B.物体的周期TA>TB
C.物体的线速度大小vA>vB
D.物体的角速度大小ωA<ωB
练3 在汽车无极变速器中,存在如图所示的装置,A是与B同轴相连的齿轮,C是与D同轴相连的齿轮,A、C、M为相互咬合的齿轮.已知齿轮A、C规格相同,半径为R,齿轮B、D规格也相同,半径为1.5R,齿轮M的半径为0.9R.当齿轮M如图方向转动时以下说法正确的是( )
A.齿轮D和齿轮B的转动方向相反
B.齿轮D和齿轮B的转动周期之比为1∶1
C.齿轮M和齿轮B边缘某点的线速度大小之比为1∶1
D.齿轮M和齿轮C的角速度大小之比为9∶10
解答传动问题要“三看、一记、二明确”
(1)三看:一看题,看题目说明的情境;二看图,看图片是同轴传动还是皮带传动;三看联系,看内部结构的各个组成部分之间是什么关系,即靠齿轮、皮带、摩擦等.
(2)一记:一记是指记公式,公式有v=ωr、T=以及v=rω==2πrn等.
(3)二明确:①在通常情况下,同轴传动的各点角速度ω、转速n和周期T相等,线速度v=ωr,即与半径成正比.②在认为皮带不打滑的情况下,传动皮带和与皮带连接的轮边缘上各点的线速度大小相等,由ω=可知,角速度与半径成反比.
随堂演练·达标自测——突出创新性 素养达标
1.关于做匀速圆周运动的物体的线速度、角速度、周期的关系,下列说法中正确的是 ( )
A.线速度大的角速度一定大
B.线速度大的周期一定小
C.角速度大的运动半径一定小
D.角速度大的周期一定小
2.一户外健身器材如图所示.当器材上轮子转动时,轮子上A、B两点的( )
A.转速nB>nA
B.周期TB>TA
C.线速度vB>vA
D.角速度ωB>ωA
3.(多选)明代出版的《天工开物》一书中就有牛力齿轮翻车的图画(如图所示),记录了我们祖先的劳动智慧.若A、B两齿轮的半径关系为rA>rB,则( )
A.齿轮A、B的角速度大小相等
B.齿轮A的角速度大小小于齿轮B的角速度大小
C.齿轮A、B边缘的线速度大小相等
D.齿轮A边缘的线速度大小小于齿轮B边缘的线速度大小
4.(多选)如图所示是中国古代玩具饮水鸟的示意图,它的神奇之处是,在鸟的面前放上一杯水,鸟就会俯下身去,把嘴浸到水里,“喝”了一口水后,鸟将绕着O点不停摆动,一会儿它又会俯下身去,再“喝”一口水.P、Q是饮水鸟上两点,且rPO>rQO,则在摆动过程中( )
A.P点的线速度小于Q点的线速度
B.P、Q两点的角速度大小相等
C.相同时间内P、Q两点通过的弧长相等
D.P、Q两点的线速度方向相反
5.火车以15 m/s的速率转过一段弯道,某乘客发现放在桌面上的指南针在10 s内匀速转过了约10°.在此10 s时间内,下列对火车的说法正确的是 ( )
A.运动路程为150 m B.加速度为零
C.角速度约为1 rad/s D.周期约为60 s
1.圆周运动
必备知识·自主学习
一、
2.v=
5.(1)处处相等 (2)变化 变速
二、
3.rad/s
三、
2.秒 s
四、
1.乘积
2.ωr
思考辨析
答案:(1)× (2)× (3)√ (4)√ (5)× (6)√
关键能力·合作探究
探究点一
提示:闹钟和手表是从不同角度看圆周运动的:闹钟指的是秒针针尖的线速度;手表则指的是描述秒针运动的另一个物理量,这个物理量就是角速度.
【例1】 【解析】 每隔2 s“点”一次奶油,蛋糕一周均匀“点”上10个奶油,则圆盘转动一圈的时间T=20 s,A错误,B正确;蛋糕边缘的奶油(可视为质点)线速度大小约为v=== m/s= m/s,C正确,D错误.
【答案】 BC
【例2】 【解析】 根据线速度定义式有v=,定位球的线速度为v= cm/s=12 cm/s,角速度与线速度关系为v=ωr,因此定位球的角速度为ω== rad/s=12 rad/s,选项D正确.
【答案】 D
【例3】 【解析】 由v=ωr知,当半径一定时,线速度越大,角速度越大,A错误;由ω=2nπ知,角速度越大,转速越大,B正确;由v=知,线速度一定时,半径越大,周期越长,C正确;由ω=知,角速度一定时,周期一定,与半径无关,D错误.
【答案】 BC
练1 解析:由题意知v=4 m/s,T=2 s,根据角速度与周期的关系可知ω==π rad/s.由线速度与角速度的关系v=ωr得r== m≈1.27 m.由v=2πnr得转速n==0.5 r/s.由频率与周期的关系得f==0.5 Hz,故选项A错误,B、C、D正确.
答案:BCD
探究点二
提示:线速度的大小和角速度的大小都相同.
【例4】 【解析】 大齿轮与小齿轮是链条传动,边缘点线速度相等,则有vA∶vB=1∶1,根据v=ωr,则有ωA∶ωB=rB∶rA=1∶3;小齿轮与后轮是同轴传动,角速度相等,则有ωB∶ωC=1∶1,根据v=ωr,则有vB∶vC=1∶10,所以角速度大小关系是ωA∶ωB∶ωC=1∶3∶3,线速度大小关系是vA∶vB∶vC=1∶1∶10,根据T=,可知TA∶TB∶TC=3∶1∶1,根据ω=2πn可知,转速之比是nA∶nB∶nC=1∶3∶3,故选项C正确.
【答案】 C
练2 解析:A对,B、D错:两物体随地球自转,同轴传动,所以角速度ω相同,根据ω=可知两物体周期相同,即ωA=ωB,TA=TB.C错:物体做圆周运动的半径由物体指向地轴,根据题图可知rA
练3 解析:A错:A、M、C三个紧密咬合的齿轮是同缘传动,因为M顺时针转动,故A逆时针转动,C逆时针转动,又A、B同轴传动,C、D同轴传动,所以齿轮D和齿轮B的转动方向相同.B对:A、M、C三个紧密咬合的齿轮是同缘传动,边缘线速度大小相同,齿轮A、C规格相同,半径为R,根据v=ωr得,A、C转动的角速度相同,A、B同轴传动,角速度相同,C、D同轴传动,角速度相同,且齿轮B、D规格也相同,所以齿轮D和齿轮B的转动周期相同.C错:A、M、C三个紧密咬合的齿轮是同缘传动,边缘线速度大小相同;A与B属于同轴传动,角速度相等,由于B的半径大于A的半径,所以B边缘的线速度大于A边缘的线速度,所以B边缘的线速度也大于M边缘的线速度.D错:A、M、C三个紧密咬合的齿轮是同缘传动,边缘线速度大小相同,根据v=ωr得:===.
答案:B
随堂演练·达标自测
1.解析:由v=ωr知,r一定时,v与ω成正比;v一定时,ω与r成反比,故A、C错误.由v=知,r一定时,v越大,T越小,故B错误.由ω=可知,ω越大,T越小,故D正确.
答案:D
2.答案:C
3.解析:齿轮A、B为齿轮传动,齿轮A、B边缘的线速度大小相等,且齿轮A的半径比齿轮B的大,根据v=ωr可知齿轮A的角速度大小小于齿轮B的角速度大小,A、D错误,B、C正确.
答案:BC
4.解析:鸟将绕着O点不停摆动,P、Q是饮水鸟上两点,属于同轴转动.P点离O点更远,绕O点转动的半径大.根据同轴转动角速度相等知P、Q两点的角速度大小相等,故B正确;P、Q两点的角速度大小相同,P点绕O点转动的半径大,根据v=ωr知,P点的线速度较大,故A错误;P、Q两点的线速度大小不同,故相同时间内通过的弧长不相等,故C错误;P、Q在O点两端,两点的线速度方向均与杆垂直,故两点的线速度方向相反,选项D正确.
答案:BD
5.解析:火车以15 m/s的速率转弯,可看成做匀速圆周运动,则在10 s内的路程为s=vt=150 m,A正确;火车做曲线运动,速度在不断变化,因此加速度一定不为零,B错误;指南针在10 s内匀速转过了约10°,又10°=×2π rad= rad,根据角速度的定义可得角速度约为ω= rad/s= rad/s,C错误;根据角速度与周期的关系可得周期为T=≈ s=360 s,D错误.
答案:A
