2021-2022学年度沪科版九年级数学上册课件 21.2.2二次函数y=ax2+bx+c的图象和性质(第3课时)(共28张PPT)
文档属性
| 名称 | 2021-2022学年度沪科版九年级数学上册课件 21.2.2二次函数y=ax2+bx+c的图象和性质(第3课时)(共28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 463.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览



文档简介
(共28张PPT)
(第3课时)
21.2.2 二次函数 y = ax +bx+c的图象和性质
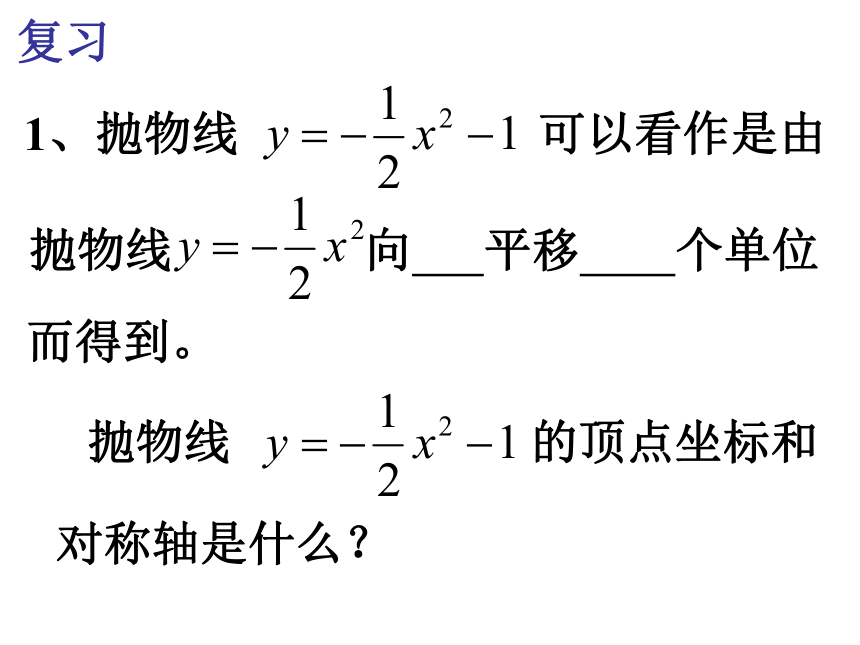
复习
1、抛物线 可以看作是由
抛物线 向 平移 个单位
而得到。
☆抛物线 的顶点坐标和
对称轴是什么?
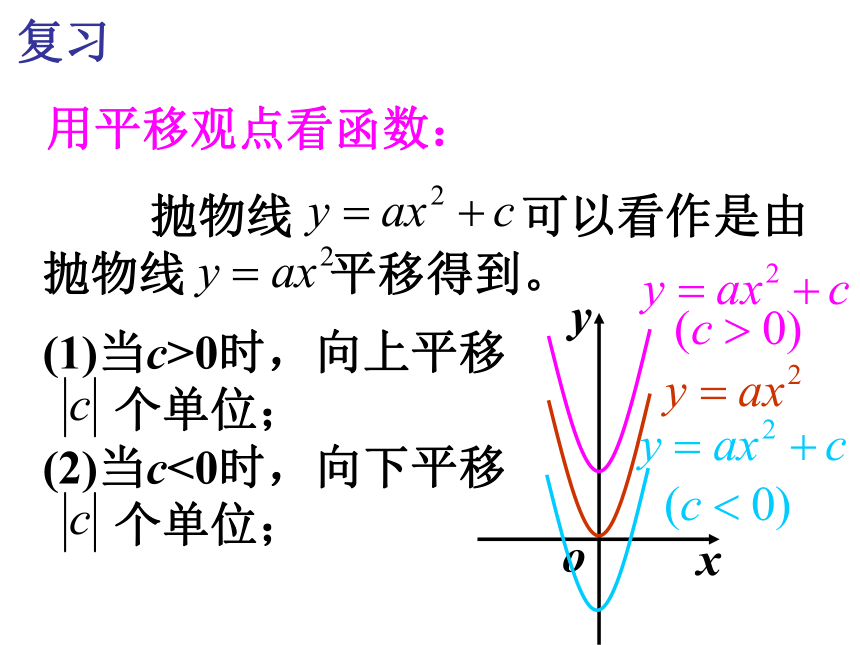
复移观点看函数:
x
y
o
抛物线 可以看作是由
抛物线 平移得到。
(1)当c>0时,向上平移
个单位;
(2)当c<0时,向下平移
个单位;
复习
2、抛物线 可以看作是由
抛物线 向 平移 个单位
而得到。
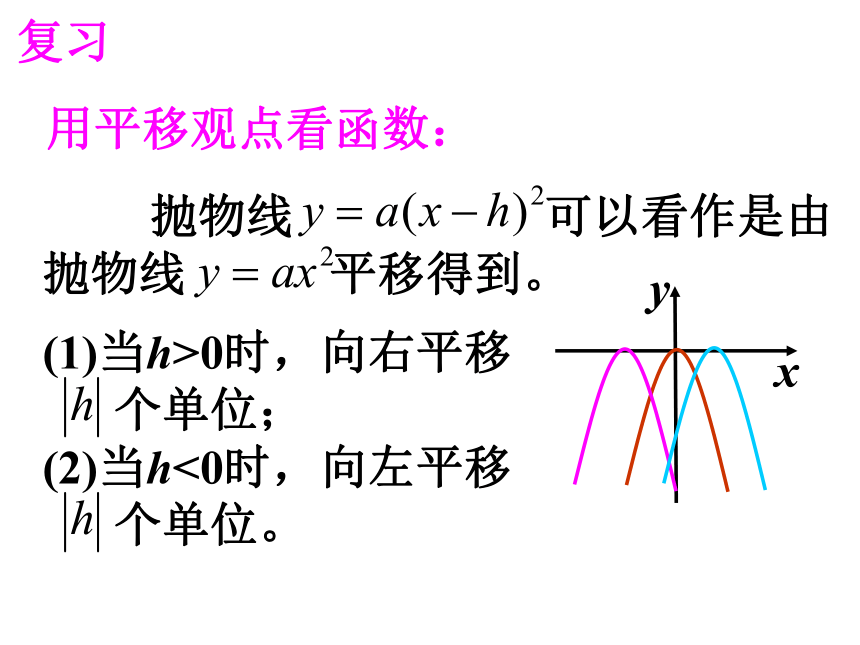
复移观点看函数:
抛物线 可以看作是由
抛物线 平移得到。
x
y
o
(1)当h>0时,向右平移
个单位;
(2)当h<0时,向左平移
个单位。
一、在同一坐标系中画二次函数的图象:
探究
探究
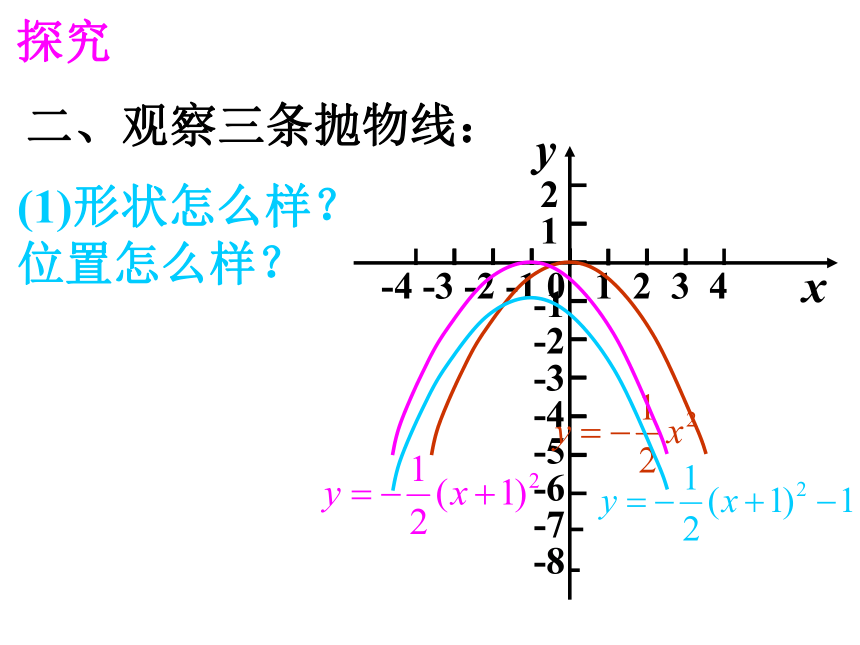
二、观察三条抛物线:
(1)形状怎么样?
位置怎么样?
-4 -3 -2 -1 0 1 2 3 4
2
1
-1
-2
-3
-4
-5
-6
-7
-8
x
y
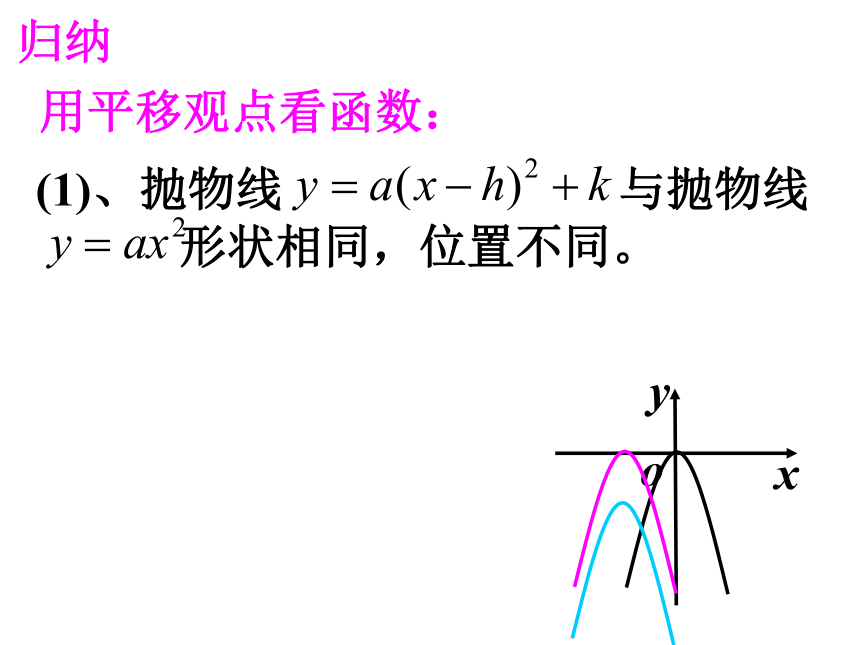
归纳
用平移观点看函数:
(1)、抛物线 与抛物线
形状相同,位置不同。
x
y
o
探究
-4 -3 -2 -1 0 1 2 3 4
2
1
-1
-2
-3
-4
-5
-6
-7
-8
x
y
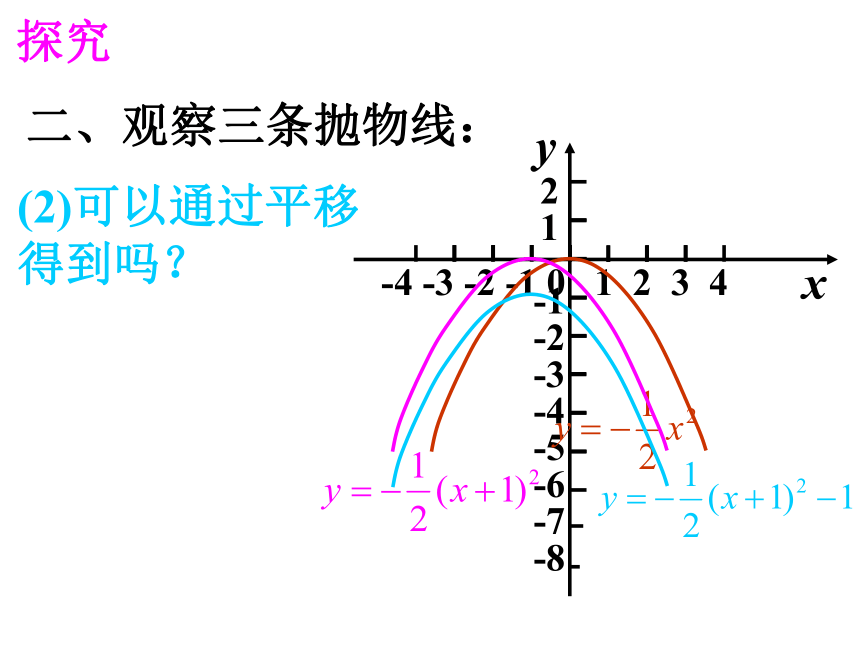
二、观察三条抛物线:
(2)可以通过平移
得到吗?
归纳
用平移观点看函数:
(1)、抛物线 与抛物线
形状相同,位置不同。
(2)、把抛物线 上下、左右平移,
可以得到抛物线 ,平
移的方向、距离要根据h、
k的值来决定。
x
y
o
巩固
3、二次函数 是由二次
函数 先向 平移 个单位,再
向 平移 个单位得到。
探究
三、观察三条抛物线:
(1)开口方向是什么?
y
-3 -2 -1 0 1 2 3
2
1
-1
-2
-3
-4
-5
-6
-7
-8
x
探究
三、观察三条抛物线:
(2)开口大小有没有
变化?
-3 -2 -1 0 1 2 3
2
1
-1
-2
-3
-4
-5
-6
-7
-8
x
探究
三、观察三条抛物线:
(3)对称轴是什么?
-3 -2 -1 0 1 2 3
2
1
-1
-2
-3
-4
-5
-6
-7
-8
x
探究
三、观察三条抛物线:
(4)顶点各是什么?
-3 -2 -1 0 1 2 3
2
1
-1
-2
-3
-4
-5
-6
-7
-8
x
探究
三、观察三条抛物线:
(5)增减性怎么样?
-3 -2 -1 0 1 2 3
2
1
-1
-2
-3
-4
-5
-6
-7
-8
x
二次函数 图象及性质:
归纳
1.图象是一条抛物线,对称轴为直线
x=h,顶点为(h,k)。
归纳
2.当a>0时,开口向上;
在对称轴的左侧,y随x的增大而减小,
在对称轴的右侧,y随x的增大而增大;
当x=h时,y取最小值为k。
二次函数 图象及性质:
归纳
3.当a<0时,开口向下;
在对称轴的左侧,y随x的增大而增大,
在对称轴的右侧,y随x的增大而减小;
当x=h时,y取最大值为k。
二次函数 图象及性质:
范例
例1、已知抛物线 .
(1)写出抛物线的开口方向、顶点M的
坐标、对称轴;
(2)作出函数的图象;
(3)写出与y轴交点C的坐标及与x轴交点
A、B的坐标;
(4)当x取何值时:①函数值y随x的增大
而增大?②函数值y随x的增大而减小?
二次函数形式之一:
归纳
做二次函数的顶
点式。
范例
例1、已知抛物线 .
(1)写出抛物线的开口方向、顶点M的
坐标、对称轴;
(2)作出函数的图象;
(3)写出与y轴交点C的坐标及与x轴交点
A、B的坐标;
(4)当x取何值时:①函数值y随x的增大
而增大?②函数值y随x的增大而减小?
范例
例1、已知抛物线 .
(5)观察函数图象,当x取何值时:
①y>0 ②y=0 ③y< 0
(6)求△ABM的面积。
巩固
4、说出下列函数图象的性质:
开口方向、对称轴、顶点、增减性、
最大(小)值。
范例
例2、已知二次函数 的图
象经过(1,0)、(0,3)两点,对称轴为
x=-1。
(1)求二次函数的解析式;
(2)设这个函数的图象与x轴的交点为A、
B(A在B的左边),与y轴的交点为C,顶
点为D,求A、B、C、D四点的坐标;
(3)求四边形ABCD的面积。
巩固
5、已知二次函数图象顶点为(-1,-6),
并且图象经过点(0,5),求这个二次函
数的解析式。
小结
(1)形状、对称轴、顶点坐标;
(2)开口方向、极值、开口大小;
(3)对称轴两侧增减性。
二次函数 图象及性质:
(第3课时)
21.2.2 二次函数 y = ax +bx+c的图象和性质
复习
1、抛物线 可以看作是由
抛物线 向 平移 个单位
而得到。
☆抛物线 的顶点坐标和
对称轴是什么?
复移观点看函数:
x
y
o
抛物线 可以看作是由
抛物线 平移得到。
(1)当c>0时,向上平移
个单位;
(2)当c<0时,向下平移
个单位;
复习
2、抛物线 可以看作是由
抛物线 向 平移 个单位
而得到。
复移观点看函数:
抛物线 可以看作是由
抛物线 平移得到。
x
y
o
(1)当h>0时,向右平移
个单位;
(2)当h<0时,向左平移
个单位。
一、在同一坐标系中画二次函数的图象:
探究
探究
二、观察三条抛物线:
(1)形状怎么样?
位置怎么样?
-4 -3 -2 -1 0 1 2 3 4
2
1
-1
-2
-3
-4
-5
-6
-7
-8
x
y
归纳
用平移观点看函数:
(1)、抛物线 与抛物线
形状相同,位置不同。
x
y
o
探究
-4 -3 -2 -1 0 1 2 3 4
2
1
-1
-2
-3
-4
-5
-6
-7
-8
x
y
二、观察三条抛物线:
(2)可以通过平移
得到吗?
归纳
用平移观点看函数:
(1)、抛物线 与抛物线
形状相同,位置不同。
(2)、把抛物线 上下、左右平移,
可以得到抛物线 ,平
移的方向、距离要根据h、
k的值来决定。
x
y
o
巩固
3、二次函数 是由二次
函数 先向 平移 个单位,再
向 平移 个单位得到。
探究
三、观察三条抛物线:
(1)开口方向是什么?
y
-3 -2 -1 0 1 2 3
2
1
-1
-2
-3
-4
-5
-6
-7
-8
x
探究
三、观察三条抛物线:
(2)开口大小有没有
变化?
-3 -2 -1 0 1 2 3
2
1
-1
-2
-3
-4
-5
-6
-7
-8
x
探究
三、观察三条抛物线:
(3)对称轴是什么?
-3 -2 -1 0 1 2 3
2
1
-1
-2
-3
-4
-5
-6
-7
-8
x
探究
三、观察三条抛物线:
(4)顶点各是什么?
-3 -2 -1 0 1 2 3
2
1
-1
-2
-3
-4
-5
-6
-7
-8
x
探究
三、观察三条抛物线:
(5)增减性怎么样?
-3 -2 -1 0 1 2 3
2
1
-1
-2
-3
-4
-5
-6
-7
-8
x
二次函数 图象及性质:
归纳
1.图象是一条抛物线,对称轴为直线
x=h,顶点为(h,k)。
归纳
2.当a>0时,开口向上;
在对称轴的左侧,y随x的增大而减小,
在对称轴的右侧,y随x的增大而增大;
当x=h时,y取最小值为k。
二次函数 图象及性质:
归纳
3.当a<0时,开口向下;
在对称轴的左侧,y随x的增大而增大,
在对称轴的右侧,y随x的增大而减小;
当x=h时,y取最大值为k。
二次函数 图象及性质:
范例
例1、已知抛物线 .
(1)写出抛物线的开口方向、顶点M的
坐标、对称轴;
(2)作出函数的图象;
(3)写出与y轴交点C的坐标及与x轴交点
A、B的坐标;
(4)当x取何值时:①函数值y随x的增大
而增大?②函数值y随x的增大而减小?
二次函数形式之一:
归纳
做二次函数的顶
点式。
范例
例1、已知抛物线 .
(1)写出抛物线的开口方向、顶点M的
坐标、对称轴;
(2)作出函数的图象;
(3)写出与y轴交点C的坐标及与x轴交点
A、B的坐标;
(4)当x取何值时:①函数值y随x的增大
而增大?②函数值y随x的增大而减小?
范例
例1、已知抛物线 .
(5)观察函数图象,当x取何值时:
①y>0 ②y=0 ③y< 0
(6)求△ABM的面积。
巩固
4、说出下列函数图象的性质:
开口方向、对称轴、顶点、增减性、
最大(小)值。
范例
例2、已知二次函数 的图
象经过(1,0)、(0,3)两点,对称轴为
x=-1。
(1)求二次函数的解析式;
(2)设这个函数的图象与x轴的交点为A、
B(A在B的左边),与y轴的交点为C,顶
点为D,求A、B、C、D四点的坐标;
(3)求四边形ABCD的面积。
巩固
5、已知二次函数图象顶点为(-1,-6),
并且图象经过点(0,5),求这个二次函
数的解析式。
小结
(1)形状、对称轴、顶点坐标;
(2)开口方向、极值、开口大小;
(3)对称轴两侧增减性。
二次函数 图象及性质:
