2021-2022学年度沪科版九年级数学上册课件 21.3 二次函数与一元二次方程(共15张PPT)
文档属性
| 名称 | 2021-2022学年度沪科版九年级数学上册课件 21.3 二次函数与一元二次方程(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览


文档简介
(共15张PPT)
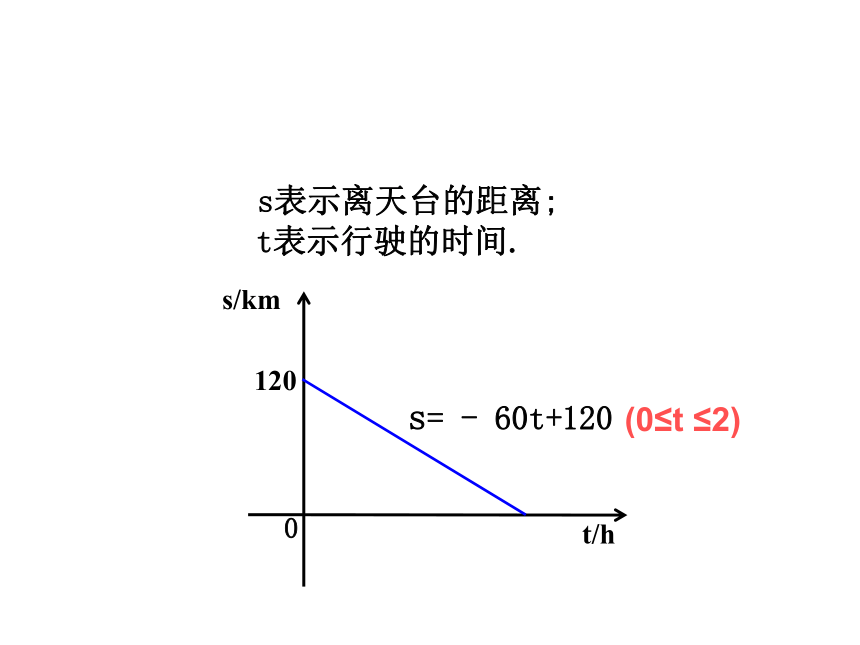
s表示离天台的距离;
t表示行驶的时间.
s= - 60t+120
120
0
t/h
s/km
(0≤t ≤2)
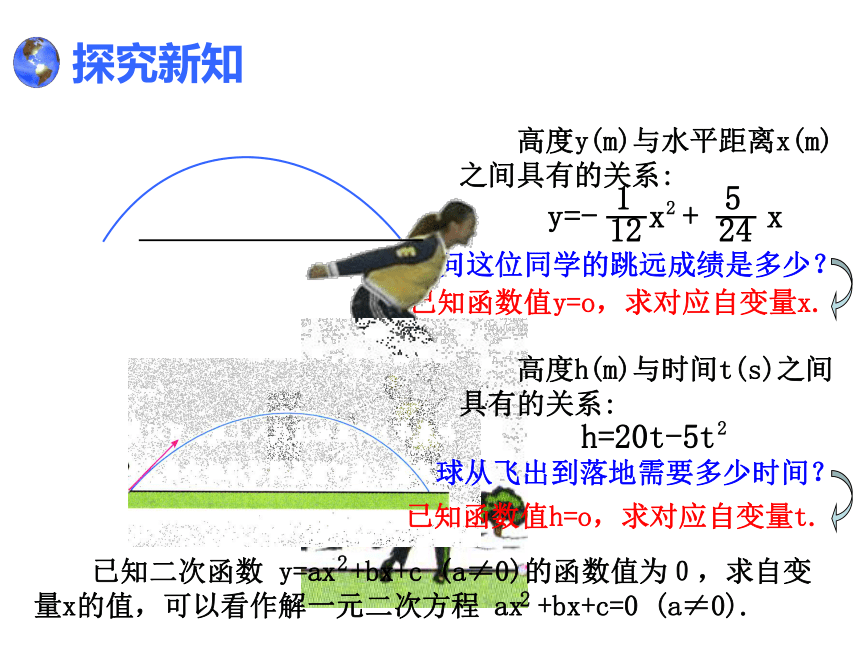
已知函数值y=o,求对应自变量x.
请问这位同学的跳远成绩是多少?
高度y(m)与水平距离x(m)之间具有的关系:
y=- x + x
1
12
2
5
24
高度h(m)与时间t(s)之间具有的关系:
h=20t-5t
2
球从飞出到落地需要多少时间?
已知函数值h=o,求对应自变量t.
已知二次函数 y=ax +bx+c (a≠0)的函数值为0,求自变量x的值,可以看作解一元二次方程 ax +bx+c=0 (a≠0).
2
2
探究新知
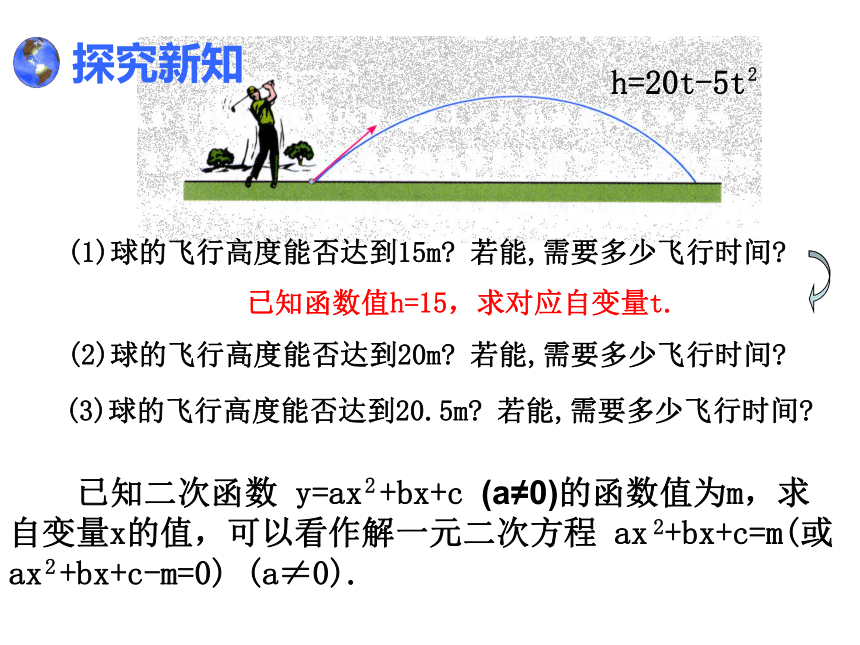
(1)球的飞行高度能否达到15m 若能,需要多少飞行时间
已知函数值h=15,求对应自变量t.
(2)球的飞行高度能否达到20m 若能,需要多少飞行时间
(3)球的飞行高度能否达到20.5m 若能,需要多少飞行时间
已知二次函数 y=ax +bx+c (a≠0)的函数值为m,求自变量x的值,可以看作解一元二次方程 ax +bx+c=m(或
ax +bx+c-m=0) (a≠0).
2
2
2
探究新知
h=20t-5t
2
归纳总结
已知二次函数 y=ax +bx+c (a≠0)的函数值为0,求自变量x的值,可以看作解一元二次方程 ax +bx+c=0 (a≠0).
2
2
已知二次函数 y=ax +bx+c (a≠0)的函数值为m,求自变量x的值,可以看作解一元二次方程 ax +bx+c=m(或
ax +bx+c-m=0) (a≠0).
2
2
2
以上关系反之也成立.
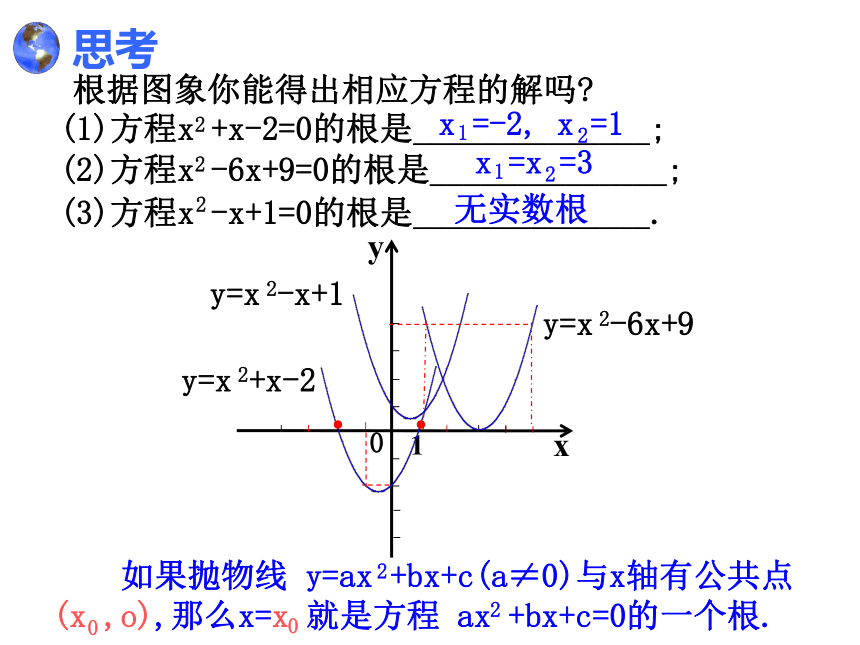
根据图象你能得出相应方程的解吗
思考
0
x
y
1
y=x +x-2
2
y=x -6x+9
2
y=x -x+1
2
.
.
(1)方程x +x-2=0的根是______________;
2
(2)方程x -6x+9=0的根是______________;
2
(3)方程x -x+1=0的根是______________.
2
如果抛物线 y=ax +bx+c(a≠0)与x轴有公共点(x ,o),那么x=x 就是方程 ax +bx+c=0的一个根.
2
2
0
0
x =-2, x =1
2
1
x =x =3
2
1
无实数根
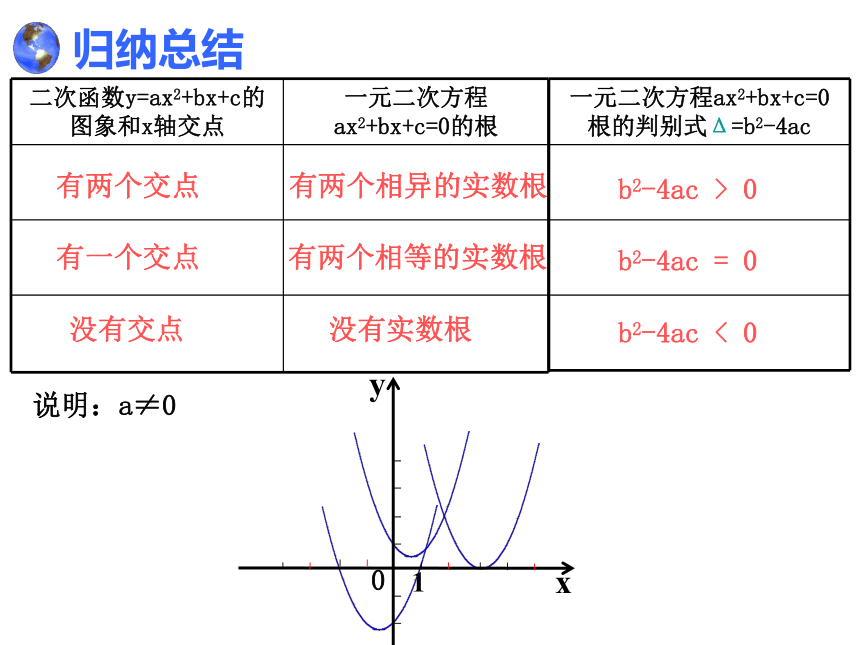
归纳总结
二次函数y=ax2+bx+c的图象和x轴交点 一元二次方程ax2+bx+c=0的根
0
x
y
1
有两个交点
有两个相异的实数根
有一个交点
有两个相等的实数根
没有交点
没有实数根
一元二次方程ax2+bx+c=0根的判别式Δ=b2-4ac
b2-4ac > 0
b2-4ac = 0
b2-4ac < 0
说明:a≠0
练一练
下列二次函数的图象与x轴有交点吗?有几个交点?
2
2
(5) y=2x - (4k+1)x+2k -1;
(1) y=2x +x-3;
2
(2) y=-4x -4x-1;
2
(3) y=3x -2x+3;
2
2
(4) y=x +(2k+1)x-k +k;
2
若此抛物线与 x轴有两个交点,求k的取值范围.
基础练习:
1.不与x轴相交的抛物线是( )
A y=2x2 – 3 B y= - 2 x2 + 3
C y= - x2 – 3x D y=-2(x+1)2 - 3
2.若抛物线y=ax2+bx+c,当 a>0,c<0时,图象与x轴交点情况是( )
A 无交点 B 只有一个交点
C 有两个交点 D不能确定
D
C
3.如果关于x的一元二次方程 x2-2x+m=0有两个相等的实数根,则m=____,此时抛物线 y=x2-2x+m与x轴有__个交点 .
4.已知抛物线 y=x2 – 8x +c的顶点在 x轴上,则c=____.
1
1
16
5.若函数y=-x2+2kx+2与坐标轴交点的个数有 个.
3
(1,0)
6.已知抛物线y=ax2+bx+c的图象如图,则关于x的方程ax2+bx+c =0根的情况是( )
A 有两个不相等的实数根
B 有两个异号的实数根
C有两个相等的实数根
D 没有实数根
x
y
O
1
2
D
-3
例: 利用函数图象求方程x2-2x-2=0的实数根
(精确到0.1)
解: 作y=x2-2x-2的图象(如图),它与x轴的公共点
的横坐标大约是 – 0.7 , 2.7
所以方程x2-2x-2=0的实数根为
x1≈-0.7, x2≈-2.7.
练习:根据下列表格的对应值:
判断方程ax2+bx+c=0 (a≠0,a,b,c为常数)一个解x的范围是( )
A 3C 3.24 x 3.23 3.24 3.25 3.26
y=ax2+bx+c -0.06 -0.02 0.03 0.09
C
升华提高
体会两种思想:
数形结合思想
弄清一种关系------函数与一元二次方程的关系
如果抛物线 y=ax +bx+c 与x轴有公共点(x ,o),那么x=x 就是方程 ax +bx+c=0的一个根.
2
2
0
0
分类讨论思想
一元二次方程ax2+bx+c=0的根
二次函数y=ax2+bx+c的图象和x轴交点
有两个交点
有两个相异的实数根
有一个交点
有两个相等的实数根
没有交点
没有实数根
一元二次方程ax2+bx+c=0根的判别式Δ=b2-4ac
b2-4ac > 0
b2-4ac = 0
b2-4ac < 0
s表示离天台的距离;
t表示行驶的时间.
s= - 60t+120
120
0
t/h
s/km
(0≤t ≤2)
已知函数值y=o,求对应自变量x.
请问这位同学的跳远成绩是多少?
高度y(m)与水平距离x(m)之间具有的关系:
y=- x + x
1
12
2
5
24
高度h(m)与时间t(s)之间具有的关系:
h=20t-5t
2
球从飞出到落地需要多少时间?
已知函数值h=o,求对应自变量t.
已知二次函数 y=ax +bx+c (a≠0)的函数值为0,求自变量x的值,可以看作解一元二次方程 ax +bx+c=0 (a≠0).
2
2
探究新知
(1)球的飞行高度能否达到15m 若能,需要多少飞行时间
已知函数值h=15,求对应自变量t.
(2)球的飞行高度能否达到20m 若能,需要多少飞行时间
(3)球的飞行高度能否达到20.5m 若能,需要多少飞行时间
已知二次函数 y=ax +bx+c (a≠0)的函数值为m,求自变量x的值,可以看作解一元二次方程 ax +bx+c=m(或
ax +bx+c-m=0) (a≠0).
2
2
2
探究新知
h=20t-5t
2
归纳总结
已知二次函数 y=ax +bx+c (a≠0)的函数值为0,求自变量x的值,可以看作解一元二次方程 ax +bx+c=0 (a≠0).
2
2
已知二次函数 y=ax +bx+c (a≠0)的函数值为m,求自变量x的值,可以看作解一元二次方程 ax +bx+c=m(或
ax +bx+c-m=0) (a≠0).
2
2
2
以上关系反之也成立.
根据图象你能得出相应方程的解吗
思考
0
x
y
1
y=x +x-2
2
y=x -6x+9
2
y=x -x+1
2
.
.
(1)方程x +x-2=0的根是______________;
2
(2)方程x -6x+9=0的根是______________;
2
(3)方程x -x+1=0的根是______________.
2
如果抛物线 y=ax +bx+c(a≠0)与x轴有公共点(x ,o),那么x=x 就是方程 ax +bx+c=0的一个根.
2
2
0
0
x =-2, x =1
2
1
x =x =3
2
1
无实数根
归纳总结
二次函数y=ax2+bx+c的图象和x轴交点 一元二次方程ax2+bx+c=0的根
0
x
y
1
有两个交点
有两个相异的实数根
有一个交点
有两个相等的实数根
没有交点
没有实数根
一元二次方程ax2+bx+c=0根的判别式Δ=b2-4ac
b2-4ac > 0
b2-4ac = 0
b2-4ac < 0
说明:a≠0
练一练
下列二次函数的图象与x轴有交点吗?有几个交点?
2
2
(5) y=2x - (4k+1)x+2k -1;
(1) y=2x +x-3;
2
(2) y=-4x -4x-1;
2
(3) y=3x -2x+3;
2
2
(4) y=x +(2k+1)x-k +k;
2
若此抛物线与 x轴有两个交点,求k的取值范围.
基础练习:
1.不与x轴相交的抛物线是( )
A y=2x2 – 3 B y= - 2 x2 + 3
C y= - x2 – 3x D y=-2(x+1)2 - 3
2.若抛物线y=ax2+bx+c,当 a>0,c<0时,图象与x轴交点情况是( )
A 无交点 B 只有一个交点
C 有两个交点 D不能确定
D
C
3.如果关于x的一元二次方程 x2-2x+m=0有两个相等的实数根,则m=____,此时抛物线 y=x2-2x+m与x轴有__个交点 .
4.已知抛物线 y=x2 – 8x +c的顶点在 x轴上,则c=____.
1
1
16
5.若函数y=-x2+2kx+2与坐标轴交点的个数有 个.
3
(1,0)
6.已知抛物线y=ax2+bx+c的图象如图,则关于x的方程ax2+bx+c =0根的情况是( )
A 有两个不相等的实数根
B 有两个异号的实数根
C有两个相等的实数根
D 没有实数根
x
y
O
1
2
D
-3
例: 利用函数图象求方程x2-2x-2=0的实数根
(精确到0.1)
解: 作y=x2-2x-2的图象(如图),它与x轴的公共点
的横坐标大约是 – 0.7 , 2.7
所以方程x2-2x-2=0的实数根为
x1≈-0.7, x2≈-2.7.
练习:根据下列表格的对应值:
判断方程ax2+bx+c=0 (a≠0,a,b,c为常数)一个解x的范围是( )
A 3
y=ax2+bx+c -0.06 -0.02 0.03 0.09
C
升华提高
体会两种思想:
数形结合思想
弄清一种关系------函数与一元二次方程的关系
如果抛物线 y=ax +bx+c 与x轴有公共点(x ,o),那么x=x 就是方程 ax +bx+c=0的一个根.
2
2
0
0
分类讨论思想
一元二次方程ax2+bx+c=0的根
二次函数y=ax2+bx+c的图象和x轴交点
有两个交点
有两个相异的实数根
有一个交点
有两个相等的实数根
没有交点
没有实数根
一元二次方程ax2+bx+c=0根的判别式Δ=b2-4ac
b2-4ac > 0
b2-4ac = 0
b2-4ac < 0
