2021-2022学年度沪科版九年级数学上册课件 21.5反比例函数(第1课时)(共26张PPT)
文档属性
| 名称 | 2021-2022学年度沪科版九年级数学上册课件 21.5反比例函数(第1课时)(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
变量
1.在某一变化过程中,不断变化的量:
常量
保持不变的量:
2.一般地,在某个变化中,有两个变量x和y,如果给定一个x的值,相应地就确定了y的一个值,那么我们称y是x的函数,其中x叫自变量.
函数的实质是两个变量之间的关系.
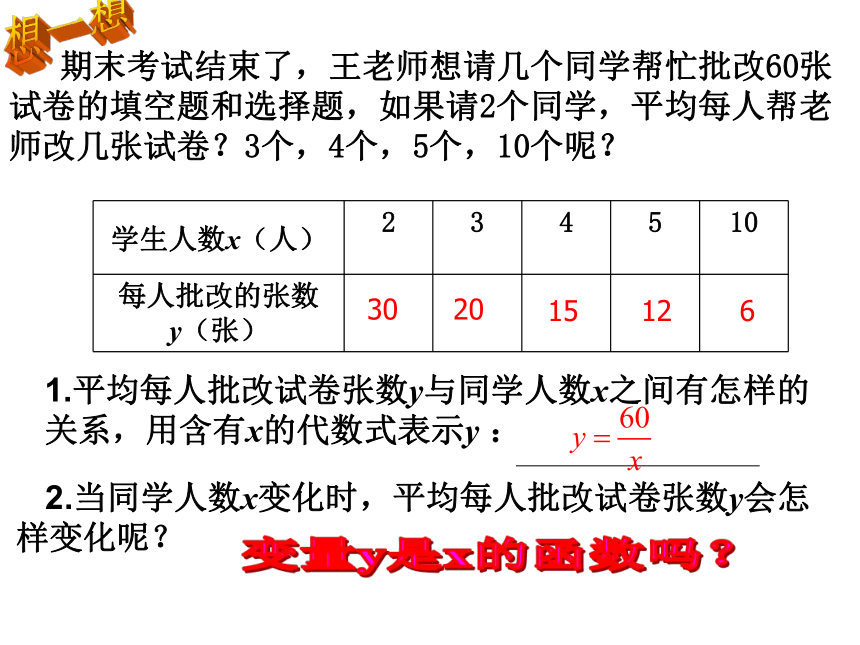
期末考试结束了,王老师想请几个同学帮忙批改60张试卷的填空题和选择题,如果请2个同学,平均每人帮老师改几张试卷?3个,4个,5个,10个呢?
学生人数x(人) 2 3 4 5 10
每人批改的张数
y(张)
2.当同学人数x变化时,平均每人批改试卷张数y会怎 样变化呢?
30
20
15
12
6
1.平均每人批改试卷张数y与同学人数x之间有怎样的关系,用含有x的代数式表示y :
活动1:
问题1:北京到杭州铁路线长为1661km. 一列火车从北京开往杭州,记火车全程的行驶时间为x(h),火车行驶的平均速度为y(km/h). (1)你能完成下列表格吗?
87.4
y(km/h)
22
17
15
12
x(h)
(2) y与x成什么比例关系?
能用一个数学解析式表示吗?
138.4
97.7
110.7
75.5
19
反比例关系
x y =1661
问题2:学校课外生物小组的同学准备自己动手,用旧围栏建一个面积为24平方米的矩形饲养场.设它的一边长为x(米),请写出另一边的长y(米)与x的关系式.
根据矩形面积可知
xy=24,
即
小组讨论: 它们有什么共同的特点?
由以上的实例中可得到如下的函数关系式:
一次函数:若两个变量x,y间的关系式可以表示成y=kx+b(k、b为常数,k≠0)的形式,则称y是x的一
次函数(x为自变量,y为因变量).
即:y=kx (k ≠ 0 ),其中k叫做比例系数.
特别地,当b=0时,称y是x的正比例函数.
注意:
常数
自变量x不能为零(因为分母为零时,该分式无意义)
xy = k
当
可以写成
时注意x的指数为-1
一般地,如果两个变量x,y之间的关系可以表示
成:
(k为常数,且k不为0)的形式,那么
称y是x的反比例函数
,且k为比例系数.
1.下列函数中哪些是反比例函数?
① ② ③ ④
y = 3x-1
y = 2x2
y =
2x
3
y =
x
1
2.下列函数中哪些是反比例函数?若是,请指出k的值.
是反比例函数时,
3.当函数
m= .
-3
(a为常数,且a≠0)
如: 在 拇指按图钉的问题 中,
当 压力 一定时, 压强 和 图钉尖的面积 成反比例函数关系.
同桌讨论:数学来源于生活,请同学们找出生活中的反比例函数关系,并举例.
某村有耕地346.2公顷,人口数量n逐年发生变化,那么该村人均占有耕地面积m(公顷/人)是全村人口数n的函数吗 是反比例函数吗 为什么
一个矩形的面积是20cm2,相邻的两条边长为xcm和ycm,那么变量y是x的函数吗 是反比例函数吗 为什么
小明同学用50元钱买学习用品,单价y(元)时与数量x(件),那么变量y是x的函数吗 是反比例函数吗 为什么
,是,是
给我一个支点,我可以撬动地球!
——阿基米德
背景知识
阻力臂
阻力
动力臂
动力
背景知识
杠杆定律
【例1】如图,阻力为1000N,阻力臂长为5cm.设动力为y(N),动力臂为x(cm).(图中杠杆本身所受重力略去不计. 杠杆平衡时:动力×动力臂=阻力×阻力臂)
(1)求y关于x的函数解析式.这个函数是反比例函数吗 如果是,请说出比例系数;
(2)求当x=50时,函数y的值,并说明这个值的实际意义;
(3)利用y关于x的函数解析式,说明当动力臂长扩大到原来的n倍时,所需动力将怎样变化?
1
1、下列函数哪些是反比例函数,
指出其中k的值.
2、 计划修建铁路1200km,那么铺轨天数y是每日铺轨量x的函数关系式是 .
y=
1200
x
3、若y是x的反比例函数,比例系数为 ,则
y关于x的函数关系式为 .
4、已知函数 是正比例函数,则
m =___ ;
已知函数 是反比例函数,则 m = ___ .
y = xm-7
y = 3xm-7
8
6
x -1 =
x
1
5、生活中有许多反比列函数的例子,在下面的实例中,x和y是否成反比例函数关系.
(1)x人共饮水10kg,平均每人饮水ykg;
(2)底面半径为xm,高为ym的圆柱形水桶的体积为∏m3
6、 一定质量的氧气,它的密度ρ(kg/m3) 是它的体积V( m3)的反比例函数,
当V=10 m3 时,ρ =2kg/ m3.
(1)求ρ与V的函数关系式;
(2)求当V=2 m3时氧气的密度.
5
若
,且
与
成正比例,比例系数为k1
与
成反比例,比例系数为k2,当
时,
当
时,
求:
(1)
1与
的关系式;
(2)求
与
的关系式;
2与
的关系式;
时,
的值.
(3)求当
再见
变量
1.在某一变化过程中,不断变化的量:
常量
保持不变的量:
2.一般地,在某个变化中,有两个变量x和y,如果给定一个x的值,相应地就确定了y的一个值,那么我们称y是x的函数,其中x叫自变量.
函数的实质是两个变量之间的关系.
期末考试结束了,王老师想请几个同学帮忙批改60张试卷的填空题和选择题,如果请2个同学,平均每人帮老师改几张试卷?3个,4个,5个,10个呢?
学生人数x(人) 2 3 4 5 10
每人批改的张数
y(张)
2.当同学人数x变化时,平均每人批改试卷张数y会怎 样变化呢?
30
20
15
12
6
1.平均每人批改试卷张数y与同学人数x之间有怎样的关系,用含有x的代数式表示y :
活动1:
问题1:北京到杭州铁路线长为1661km. 一列火车从北京开往杭州,记火车全程的行驶时间为x(h),火车行驶的平均速度为y(km/h). (1)你能完成下列表格吗?
87.4
y(km/h)
22
17
15
12
x(h)
(2) y与x成什么比例关系?
能用一个数学解析式表示吗?
138.4
97.7
110.7
75.5
19
反比例关系
x y =1661
问题2:学校课外生物小组的同学准备自己动手,用旧围栏建一个面积为24平方米的矩形饲养场.设它的一边长为x(米),请写出另一边的长y(米)与x的关系式.
根据矩形面积可知
xy=24,
即
小组讨论: 它们有什么共同的特点?
由以上的实例中可得到如下的函数关系式:
一次函数:若两个变量x,y间的关系式可以表示成y=kx+b(k、b为常数,k≠0)的形式,则称y是x的一
次函数(x为自变量,y为因变量).
即:y=kx (k ≠ 0 ),其中k叫做比例系数.
特别地,当b=0时,称y是x的正比例函数.
注意:
常数
自变量x不能为零(因为分母为零时,该分式无意义)
xy = k
当
可以写成
时注意x的指数为-1
一般地,如果两个变量x,y之间的关系可以表示
成:
(k为常数,且k不为0)的形式,那么
称y是x的反比例函数
,且k为比例系数.
1.下列函数中哪些是反比例函数?
① ② ③ ④
y = 3x-1
y = 2x2
y =
2x
3
y =
x
1
2.下列函数中哪些是反比例函数?若是,请指出k的值.
是反比例函数时,
3.当函数
m= .
-3
(a为常数,且a≠0)
如: 在 拇指按图钉的问题 中,
当 压力 一定时, 压强 和 图钉尖的面积 成反比例函数关系.
同桌讨论:数学来源于生活,请同学们找出生活中的反比例函数关系,并举例.
某村有耕地346.2公顷,人口数量n逐年发生变化,那么该村人均占有耕地面积m(公顷/人)是全村人口数n的函数吗 是反比例函数吗 为什么
一个矩形的面积是20cm2,相邻的两条边长为xcm和ycm,那么变量y是x的函数吗 是反比例函数吗 为什么
小明同学用50元钱买学习用品,单价y(元)时与数量x(件),那么变量y是x的函数吗 是反比例函数吗 为什么
,是,是
给我一个支点,我可以撬动地球!
——阿基米德
背景知识
阻力臂
阻力
动力臂
动力
背景知识
杠杆定律
【例1】如图,阻力为1000N,阻力臂长为5cm.设动力为y(N),动力臂为x(cm).(图中杠杆本身所受重力略去不计. 杠杆平衡时:动力×动力臂=阻力×阻力臂)
(1)求y关于x的函数解析式.这个函数是反比例函数吗 如果是,请说出比例系数;
(2)求当x=50时,函数y的值,并说明这个值的实际意义;
(3)利用y关于x的函数解析式,说明当动力臂长扩大到原来的n倍时,所需动力将怎样变化?
1
1、下列函数哪些是反比例函数,
指出其中k的值.
2、 计划修建铁路1200km,那么铺轨天数y是每日铺轨量x的函数关系式是 .
y=
1200
x
3、若y是x的反比例函数,比例系数为 ,则
y关于x的函数关系式为 .
4、已知函数 是正比例函数,则
m =___ ;
已知函数 是反比例函数,则 m = ___ .
y = xm-7
y = 3xm-7
8
6
x -1 =
x
1
5、生活中有许多反比列函数的例子,在下面的实例中,x和y是否成反比例函数关系.
(1)x人共饮水10kg,平均每人饮水ykg;
(2)底面半径为xm,高为ym的圆柱形水桶的体积为∏m3
6、 一定质量的氧气,它的密度ρ(kg/m3) 是它的体积V( m3)的反比例函数,
当V=10 m3 时,ρ =2kg/ m3.
(1)求ρ与V的函数关系式;
(2)求当V=2 m3时氧气的密度.
5
若
,且
与
成正比例,比例系数为k1
与
成反比例,比例系数为k2,当
时,
当
时,
求:
(1)
1与
的关系式;
(2)求
与
的关系式;
2与
的关系式;
时,
的值.
(3)求当
再见
