2021-2022学年度沪科版九年级数学上册课件 22.1 比例线段(第2课时)(共16张PPT)
文档属性
| 名称 | 2021-2022学年度沪科版九年级数学上册课件 22.1 比例线段(第2课时)(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 439.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
22.1比例线段
(第2课时)
如图,把△ABC放大一定的倍数,就得到和它相似的△ A B C
A
B
C
'
A
B
C
所以研究相似图形,先要学习线段的比和比例线段的有关知识。
A
B
C
D
E
A
B
C
D
E
如图,把五边形ABCDE缩小一定的倍数就得到和它相似的五边形A B C D E .
线段的比
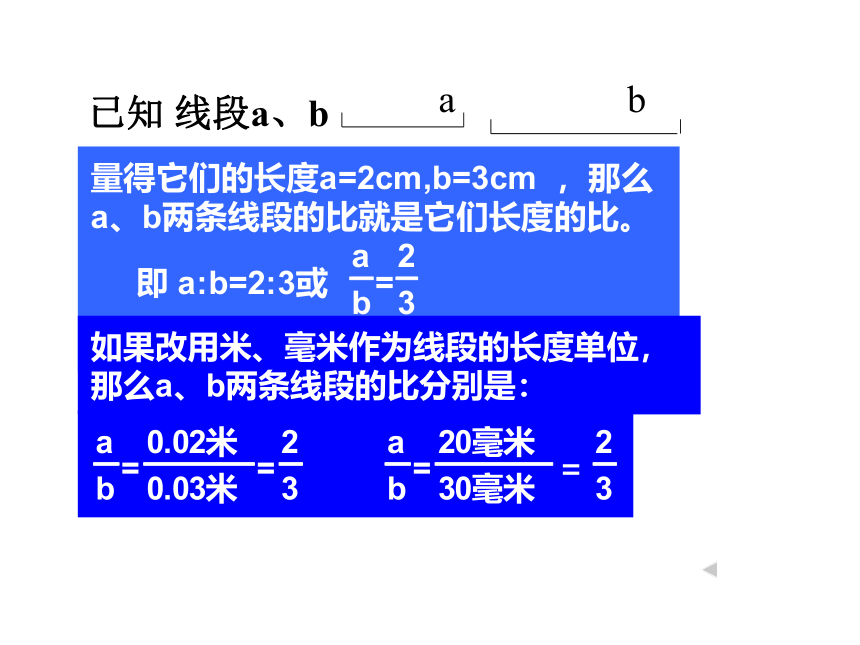
定义:在同一长度单位下,两条线段的长度的比叫做这两条线段的比。
已知 线段a、b
a
b
注意:
1.若a:b=k , 说明a是b的k倍.
2.两条线段的比与所采用的长度单位
无关,但求比时两条线段的长度单
位必须一致.
3.两条线段的比值是一个没有单位的
正数.
4.除了a=b外,a:b≠b:a,
互为倒数.
试一试
(1)a=2m , b=0.4m ;
(2)a=6cm , b=6m ;
(3)a=50mm , b=6cm ;
(4)a=3m , b=10mm .
求下列各题中 a:b 的值.
答: (1) a:b=5;
(2) a:b=1:100;
(3) a:b=5:6;
(4) a:b=300.
四条线段 a、b、c、d 中,
如果 a:b=c:d,
那么这四条线段a、b、c、d 叫做
成比例的线段,
简称比例线段.
B
C
D
A
50
25
B`
C`
D`
A`
20
10
AB 50
BC 25
∵ = =2,
A`B` 20
B`C` 10
= =2,
AB A`B`
BC B`C`
∴ = .
因此,AB、BC、A`B`、B`C`是成比例线段.
已知四条线段a、b、c、d ,
如果
a c
b d
= ,
或 a:b=c:d,
那么 a、b、c、d 叫做组成比例的项,
线段 a、d 叫做比例外项,
线段 b、c 叫做比例内项,
线段 d 叫做 a、b、c的第四比例项.
如果作为比例内项的是两条相同的线段 ,
即
a b
b c
= ,
或 a:b=b:c,
那么线段 b 叫做线段 a 和 c 的比例中项.
已知线段a=10mm,b=6cm,c=2cm,d=3cm.问:这四条线段是否成比例?为什么
解:这四条线段成比例
∵a=10mm=1cm
想一想:是否还可以写出其他几组成比例的线段.
你还有其他方法验证吗?
判断四条线段是否成比例的方法有哪些
(1)把四条线段按大小排列好,判断前两条线段的比和后两条线段的比是否相等。
(2)查看是否有两条线段的积等于其余两条线段的积 。
1.已知线段a=2cm,b=4.1cm,c=4cm,d=8.2cm,下面哪个选项是正确的?( )
A. d, b, a, c成比例线段 B. a, d, b, c成比例线段
C. a, c, b, d成比例线段 D. a, d, c, b成比例线段
2.下列各组线段的长度成比例的是( )
A.2cm,3cm,4cm,1cm B.1.5cm,2.5cm,6.5cm,4.5cm
C.1.1cm,2.2cm,3.3cm,4.4cm D.1cm,2cm,2cm,4cm
C
D
练 习
回顾与思考
1、你有什么收获?
2、学习线段比时应注意什么?
1)、两条线段的长度必须用同一单位表示;
2)、两条线段的比没有单位(与采用的单位无
关系),是一个正数;
3)、两条线段的比的表示方法。
再见
22.1比例线段
(第2课时)
如图,把△ABC放大一定的倍数,就得到和它相似的△ A B C
A
B
C
'
A
B
C
所以研究相似图形,先要学习线段的比和比例线段的有关知识。
A
B
C
D
E
A
B
C
D
E
如图,把五边形ABCDE缩小一定的倍数就得到和它相似的五边形A B C D E .
线段的比
定义:在同一长度单位下,两条线段的长度的比叫做这两条线段的比。
已知 线段a、b
a
b
注意:
1.若a:b=k , 说明a是b的k倍.
2.两条线段的比与所采用的长度单位
无关,但求比时两条线段的长度单
位必须一致.
3.两条线段的比值是一个没有单位的
正数.
4.除了a=b外,a:b≠b:a,
互为倒数.
试一试
(1)a=2m , b=0.4m ;
(2)a=6cm , b=6m ;
(3)a=50mm , b=6cm ;
(4)a=3m , b=10mm .
求下列各题中 a:b 的值.
答: (1) a:b=5;
(2) a:b=1:100;
(3) a:b=5:6;
(4) a:b=300.
四条线段 a、b、c、d 中,
如果 a:b=c:d,
那么这四条线段a、b、c、d 叫做
成比例的线段,
简称比例线段.
B
C
D
A
50
25
B`
C`
D`
A`
20
10
AB 50
BC 25
∵ = =2,
A`B` 20
B`C` 10
= =2,
AB A`B`
BC B`C`
∴ = .
因此,AB、BC、A`B`、B`C`是成比例线段.
已知四条线段a、b、c、d ,
如果
a c
b d
= ,
或 a:b=c:d,
那么 a、b、c、d 叫做组成比例的项,
线段 a、d 叫做比例外项,
线段 b、c 叫做比例内项,
线段 d 叫做 a、b、c的第四比例项.
如果作为比例内项的是两条相同的线段 ,
即
a b
b c
= ,
或 a:b=b:c,
那么线段 b 叫做线段 a 和 c 的比例中项.
已知线段a=10mm,b=6cm,c=2cm,d=3cm.问:这四条线段是否成比例?为什么
解:这四条线段成比例
∵a=10mm=1cm
想一想:是否还可以写出其他几组成比例的线段.
你还有其他方法验证吗?
判断四条线段是否成比例的方法有哪些
(1)把四条线段按大小排列好,判断前两条线段的比和后两条线段的比是否相等。
(2)查看是否有两条线段的积等于其余两条线段的积 。
1.已知线段a=2cm,b=4.1cm,c=4cm,d=8.2cm,下面哪个选项是正确的?( )
A. d, b, a, c成比例线段 B. a, d, b, c成比例线段
C. a, c, b, d成比例线段 D. a, d, c, b成比例线段
2.下列各组线段的长度成比例的是( )
A.2cm,3cm,4cm,1cm B.1.5cm,2.5cm,6.5cm,4.5cm
C.1.1cm,2.2cm,3.3cm,4.4cm D.1cm,2cm,2cm,4cm
C
D
练 习
回顾与思考
1、你有什么收获?
2、学习线段比时应注意什么?
1)、两条线段的长度必须用同一单位表示;
2)、两条线段的比没有单位(与采用的单位无
关系),是一个正数;
3)、两条线段的比的表示方法。
再见
