2021-2022学年度沪科版九年级数学上册课件 22.1 比例线段(第3课时)(共24张PPT)
文档属性
| 名称 | 2021-2022学年度沪科版九年级数学上册课件 22.1 比例线段(第3课时)(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 748.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
22.1比例线段
(第3课时)
已知四条线段a、b、c、d ,
如果
a c
b d
= ,
或 a:b=c:d,
那么 a、b、c、d 叫做组成比例的项,
线段 a、d 叫做比例外项,
线段 b、c 叫做比例内项,
线段 d 叫做 a、b、c的第四比例项.
知识回顾
两条线段的比是它们的长度的比,也就是两个数的比.关于成比例的数具有下面的性质.
比例式是等式,
因而具有等式的各个性质,
此外还有一些特殊性质:
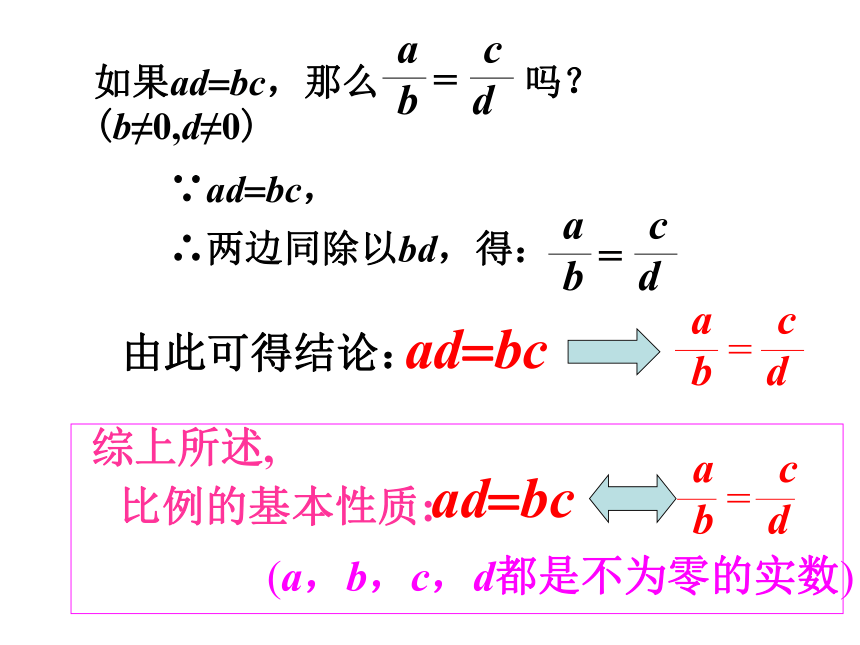
∵ad=bc,
a c
b d
=
如果ad=bc,那么 吗? (b≠0,d≠0)
a c
b d
=
∴两边同除以bd,得:
由此可得结论:
ad=bc
a c
b d
=
比例的基本性质:
ad=bc
a c
b d
=
综上所述,
(a,b,c,d都是不为零的实数)
(1)比例的基本性质
a:b=c:d ad=bc.
特殊地说:
a:b=b:c b =ac.
2
综合地说:
例1:
根据下列条件,求 的值.
练习:
如果
PA PC
PB PD
= ,
那么 PA·
PD=
如果
CD DF
EB AD
= ,
那么 AD·
CD=
如果
AC BD
EF EA
= ,
那么 EF·
BD=
如果
HE HF
NF NK
= ,
那么 HF·
NF=
PB·PC;
EB·DF;
AC·EA;
HE·NK;
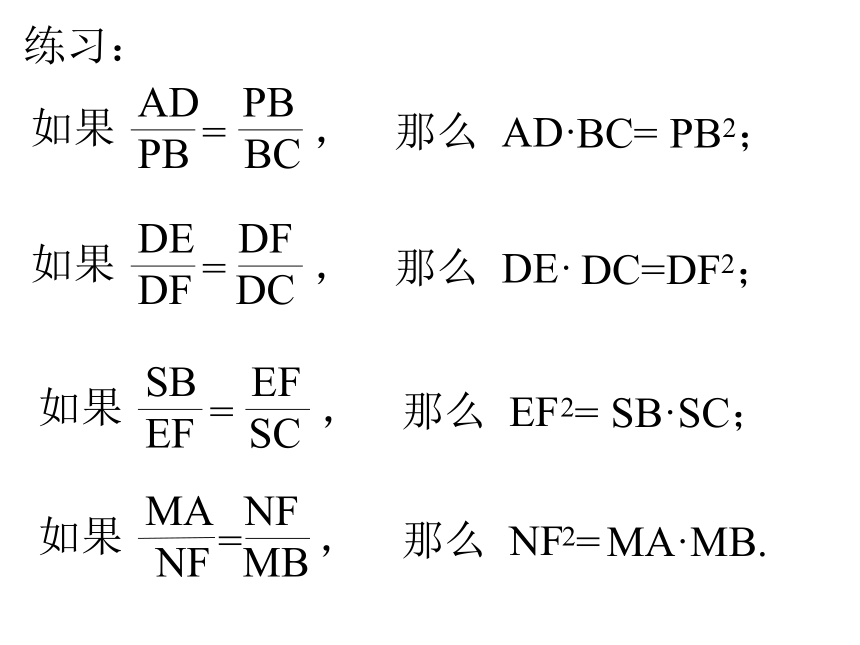
练习:
如果
AD PB
PB BC
= ,
那么 AD·
BC=
如果
DE DF
DF DC
= ,
那么 DE·
DC=
如果
SB EF
EF SC
= ,
那么 EF
2=
如果
MA NF
NF MB
= ,
那么 NF
2=
PB2;
DF2;
SB·SC;
MA·MB.
说明:
(1)一个等积式可以改写成八个比例式
(比值各不相同);
(2)对调比例式的内项或外项,
比例式仍然成立
(比值变了).
a c
b d
=
a b
c d
=
d c
b a
= .
说明:
同时对调比例式两边的比的前后项,
比例式仍然成立
(比值变了).
a c
b d
=
b d
a c
= .
已知 判断下例比例是否成立,并说明理由.
a c
b d
= ,
(2)合比性质
如果
a c
b d
= ,
那么
a±b c±d
b d
= .
练习:
如图,已知
AC
BC
= ,
那么
AB DE
BC EF
= ,
DF
EF
理由:
AB DE
BC EF
=
AC DF
BC EF
= .
AB+BC DE+EF
BC EF
=
A
B
C
D
E
F
练习:
如图,已知
AC
AB
= ,
那么
AB DE
BC EF
= ,
DF
DE
理由:
AB DE
BC EF
=
AB+BC DE+EF
AB DE
=
BC EF
AB DE
=
AC DF
AB DE
= .
A
B
C
D
E
F
(3)等比性质
如果
那么
a c
b d
=
m
n
= …=
(b+d+…+n≠0),
a+c+…+m
b+d+…+n
= .
a
b
a c
b d
=
m
n
= …=
证明:
设
=k,
则
a=bk,
c=dk,
…
,m=nk,
∴ =
a+c+…+m
b+d+…+n
bk+dk+…+nk
b+d+…+n
=
(b+d+…+n)k
b+d+…+n
=k
= .
a
b
a c
b d
=
m
n
= …=
a+c+…+m
b+d+…+n
= .
a
b
?
练习:
如图,已知
AE
AB
= ,
那么
BE CF
AB AC
= ,
A
B
C
E
F
AF
AC
理由:
BE CF
AB AC
=
AC CF
AB BE
=
AC –CF
AB –BE
=
AF AC
AE AB
=
AE AF
AB AC
= .
AF AE
AC AB
=
AC–CF AC
AB–BE AB
=
AB–BE≠0
x+y 5 x
3y 4 y
例2 已知 = ,求 .
解:
∵ = ,
x+y 5
3y 4
x+y 15
y 4
∴ = ,
x+y–y 15–4
y 4
∴ = ,
x 11
y 4
∴ = .
例3 已知 a:b:c=2:5:6,
求 的值.
2a+5b–c
3a–2b+c
解:
设 = = = k,
a b c
2 5 6
则 a=2k,
b=5k,
c=6k,
2a+5b–c
3a–2b+c
∴ =
4k+25k–6k
6k–10k+6k
=
23
2
.
例4 已知:如图, = = ,
OA OB 3
OC OD 2
求:(1) ; (2) .
OA
AC
OA+OB
OC+OD
O
A
B
C
D
分析:(1)
OA
AC
OA
OA+OC
OA+OC
OA
OC
OA
=
2
3
.
例4 已知:如图, = = ,
OA OB 3
OC OD 2
求:(1) ; (2) .
OA
AC
OA+OB
OC+OD
解:(1)
OC
OA
∴ = ,
2
3
OA 3
OC 2
∵ = ,
OA+OC
OA
∴ = ,
5
3
AC 5
OA 3
即 = ,
OA 3
AC 5
∴ = .
O
A
B
C
D
例4 已知:如图, = = ,
OA OB 3
OC OD 2
求:(1) ; (2) .
OA
AC
OA+OB
OC+OD
解:(2)
OA+OB
OC+OD
∴ = .
3
2
OA OB 3
OC OD 2
∵ = = ,
O
A
B
C
D
本课小结:
主要内容:
比例的3个主要性质及其应用.
能力要求:
通过本课的学习,
形成比例变形的能力,
要做一定量的习题,达到熟练.
再见
22.1比例线段
(第3课时)
已知四条线段a、b、c、d ,
如果
a c
b d
= ,
或 a:b=c:d,
那么 a、b、c、d 叫做组成比例的项,
线段 a、d 叫做比例外项,
线段 b、c 叫做比例内项,
线段 d 叫做 a、b、c的第四比例项.
知识回顾
两条线段的比是它们的长度的比,也就是两个数的比.关于成比例的数具有下面的性质.
比例式是等式,
因而具有等式的各个性质,
此外还有一些特殊性质:
∵ad=bc,
a c
b d
=
如果ad=bc,那么 吗? (b≠0,d≠0)
a c
b d
=
∴两边同除以bd,得:
由此可得结论:
ad=bc
a c
b d
=
比例的基本性质:
ad=bc
a c
b d
=
综上所述,
(a,b,c,d都是不为零的实数)
(1)比例的基本性质
a:b=c:d ad=bc.
特殊地说:
a:b=b:c b =ac.
2
综合地说:
例1:
根据下列条件,求 的值.
练习:
如果
PA PC
PB PD
= ,
那么 PA·
PD=
如果
CD DF
EB AD
= ,
那么 AD·
CD=
如果
AC BD
EF EA
= ,
那么 EF·
BD=
如果
HE HF
NF NK
= ,
那么 HF·
NF=
PB·PC;
EB·DF;
AC·EA;
HE·NK;
练习:
如果
AD PB
PB BC
= ,
那么 AD·
BC=
如果
DE DF
DF DC
= ,
那么 DE·
DC=
如果
SB EF
EF SC
= ,
那么 EF
2=
如果
MA NF
NF MB
= ,
那么 NF
2=
PB2;
DF2;
SB·SC;
MA·MB.
说明:
(1)一个等积式可以改写成八个比例式
(比值各不相同);
(2)对调比例式的内项或外项,
比例式仍然成立
(比值变了).
a c
b d
=
a b
c d
=
d c
b a
= .
说明:
同时对调比例式两边的比的前后项,
比例式仍然成立
(比值变了).
a c
b d
=
b d
a c
= .
已知 判断下例比例是否成立,并说明理由.
a c
b d
= ,
(2)合比性质
如果
a c
b d
= ,
那么
a±b c±d
b d
= .
练习:
如图,已知
AC
BC
= ,
那么
AB DE
BC EF
= ,
DF
EF
理由:
AB DE
BC EF
=
AC DF
BC EF
= .
AB+BC DE+EF
BC EF
=
A
B
C
D
E
F
练习:
如图,已知
AC
AB
= ,
那么
AB DE
BC EF
= ,
DF
DE
理由:
AB DE
BC EF
=
AB+BC DE+EF
AB DE
=
BC EF
AB DE
=
AC DF
AB DE
= .
A
B
C
D
E
F
(3)等比性质
如果
那么
a c
b d
=
m
n
= …=
(b+d+…+n≠0),
a+c+…+m
b+d+…+n
= .
a
b
a c
b d
=
m
n
= …=
证明:
设
=k,
则
a=bk,
c=dk,
…
,m=nk,
∴ =
a+c+…+m
b+d+…+n
bk+dk+…+nk
b+d+…+n
=
(b+d+…+n)k
b+d+…+n
=k
= .
a
b
a c
b d
=
m
n
= …=
a+c+…+m
b+d+…+n
= .
a
b
?
练习:
如图,已知
AE
AB
= ,
那么
BE CF
AB AC
= ,
A
B
C
E
F
AF
AC
理由:
BE CF
AB AC
=
AC CF
AB BE
=
AC –CF
AB –BE
=
AF AC
AE AB
=
AE AF
AB AC
= .
AF AE
AC AB
=
AC–CF AC
AB–BE AB
=
AB–BE≠0
x+y 5 x
3y 4 y
例2 已知 = ,求 .
解:
∵ = ,
x+y 5
3y 4
x+y 15
y 4
∴ = ,
x+y–y 15–4
y 4
∴ = ,
x 11
y 4
∴ = .
例3 已知 a:b:c=2:5:6,
求 的值.
2a+5b–c
3a–2b+c
解:
设 = = = k,
a b c
2 5 6
则 a=2k,
b=5k,
c=6k,
2a+5b–c
3a–2b+c
∴ =
4k+25k–6k
6k–10k+6k
=
23
2
.
例4 已知:如图, = = ,
OA OB 3
OC OD 2
求:(1) ; (2) .
OA
AC
OA+OB
OC+OD
O
A
B
C
D
分析:(1)
OA
AC
OA
OA+OC
OA+OC
OA
OC
OA
=
2
3
.
例4 已知:如图, = = ,
OA OB 3
OC OD 2
求:(1) ; (2) .
OA
AC
OA+OB
OC+OD
解:(1)
OC
OA
∴ = ,
2
3
OA 3
OC 2
∵ = ,
OA+OC
OA
∴ = ,
5
3
AC 5
OA 3
即 = ,
OA 3
AC 5
∴ = .
O
A
B
C
D
例4 已知:如图, = = ,
OA OB 3
OC OD 2
求:(1) ; (2) .
OA
AC
OA+OB
OC+OD
解:(2)
OA+OB
OC+OD
∴ = .
3
2
OA OB 3
OC OD 2
∵ = = ,
O
A
B
C
D
本课小结:
主要内容:
比例的3个主要性质及其应用.
能力要求:
通过本课的学习,
形成比例变形的能力,
要做一定量的习题,达到熟练.
再见
