2021-2022学年度沪科版九年级数学上册课件 22.3 相似三角形的性质(第2课时)(共22张PPT)
文档属性
| 名称 | 2021-2022学年度沪科版九年级数学上册课件 22.3 相似三角形的性质(第2课时)(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 998.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览


文档简介
(共22张PPT)
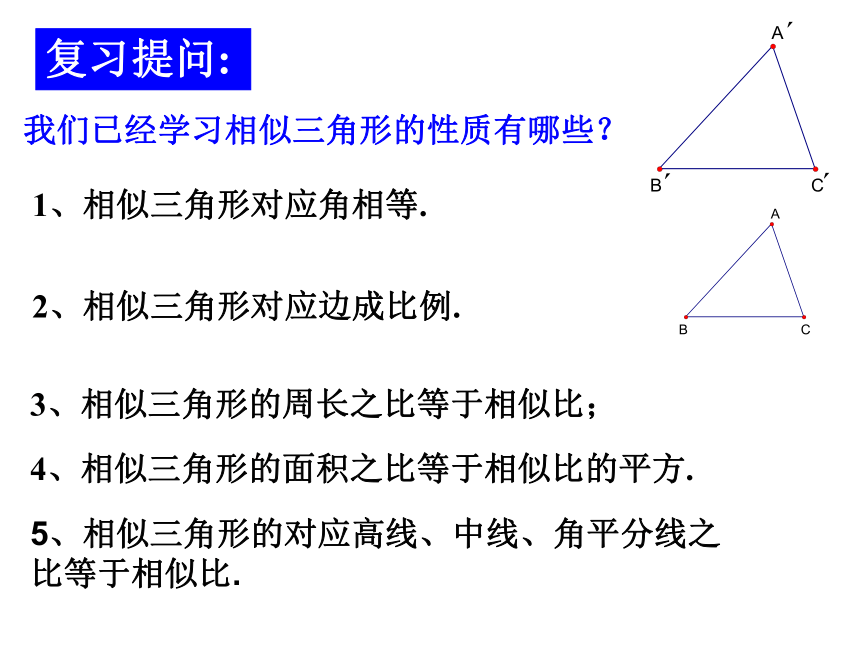
复习提问:
我们已经学习相似三角形的性质有哪些?
1、相似三角形对应角相等.
2、相似三角形对应边成比例.
3、相似三角形的周长之比等于相似比;
4、相似三角形的面积之比等于相似比的平方.
5、相似三角形的对应高线、中线、角平分线之比等于相似比.
校园里有一棵大铁树,要测量树的高度,
你有什么方法?
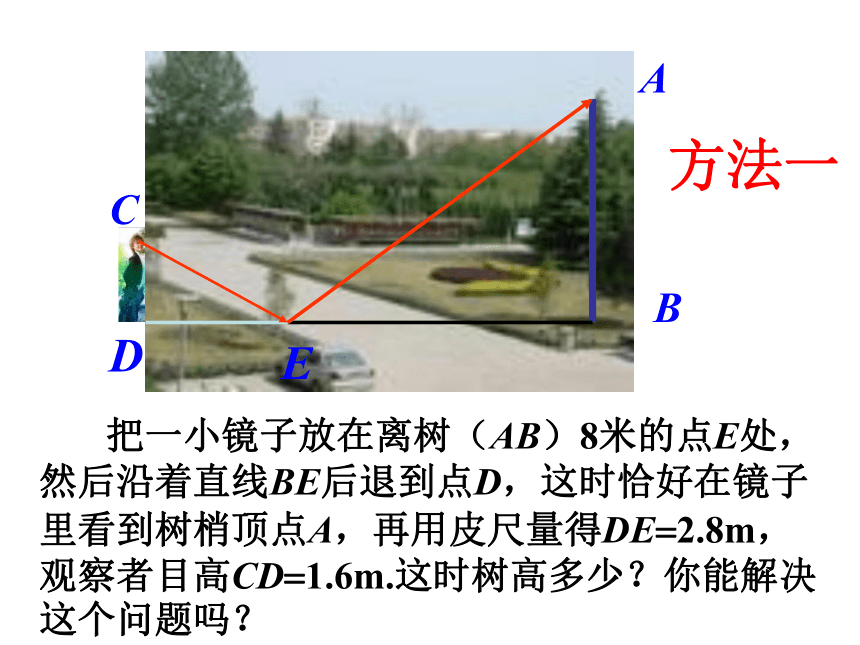
把一小镜子放在离树(AB)8米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.8m,观察者目高CD=1.6m.这时树高多少?你能解决这个问题吗?
A
B
E
D
C
方法一
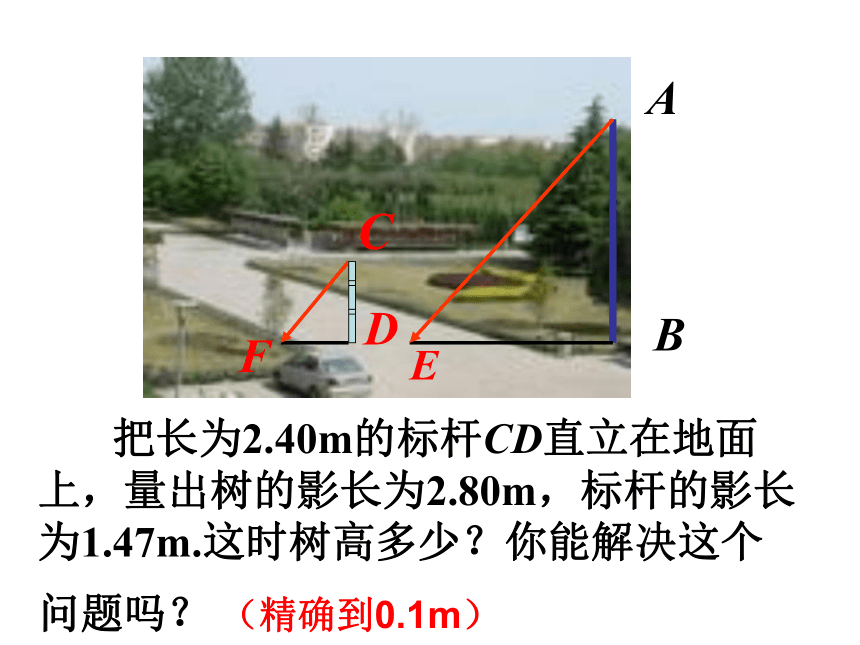
把长为2.40m的标杆CD直立在地面上,量出树的影长为2.80m,标杆的影长为1.47m.这时树高多少?你能解决这个问题吗? (精确到0.1m)
A
B
C
D
E
F
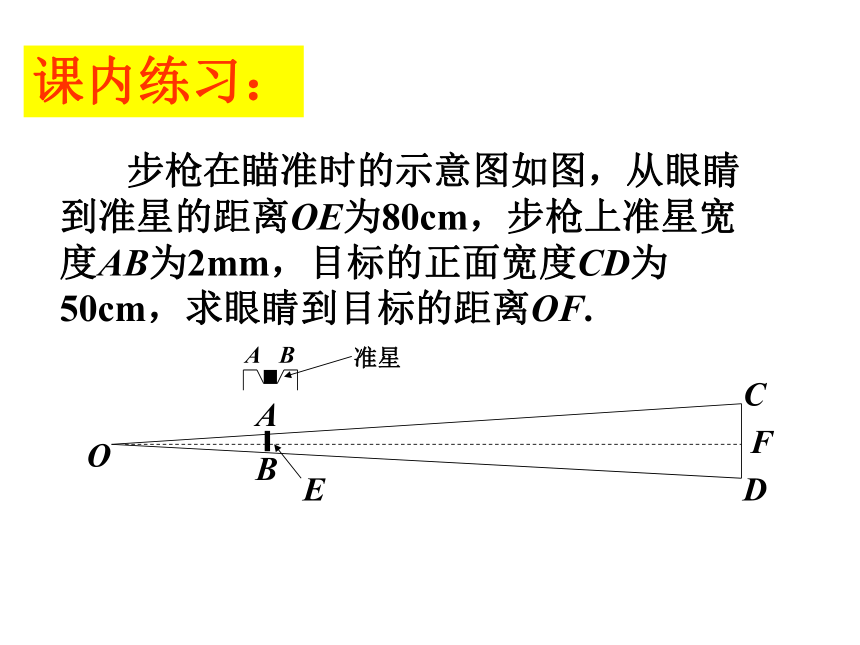
课内练习:
步枪在瞄准时的示意图如图,从眼睛到准星的距离OE为80cm,步枪上准星宽度AB为2mm,目标的正面宽度CD为50cm,求眼睛到目标的距离OF.
E
A
B
O
C
D
F
准星
A
B
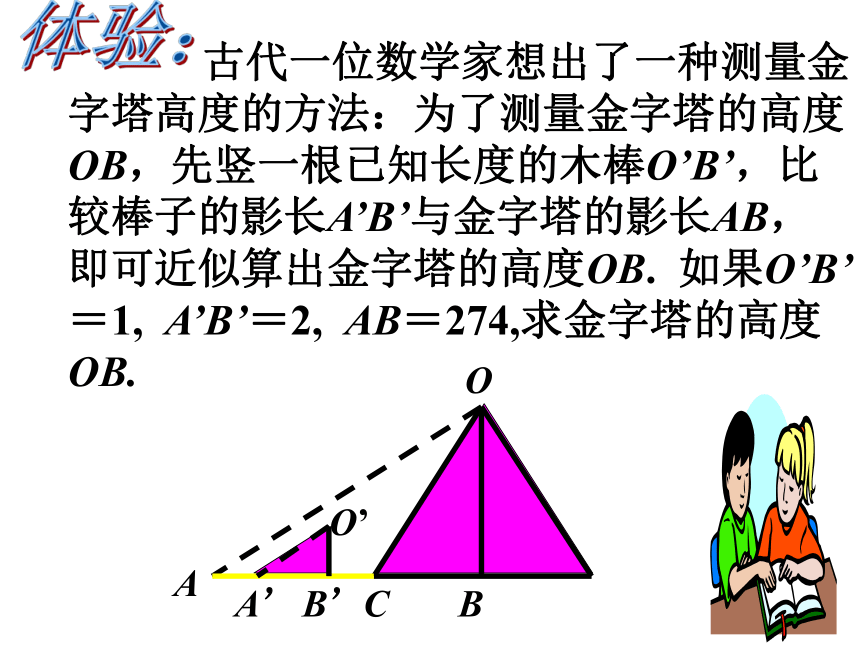
古代一位数学家想出了一种测量金字塔高度的方法:为了测量金字塔的高度OB,先竖一根已知长度的木棒O’B’,比较棒子的影长A’B’与金字塔的影长AB,即可近似算出金字塔的高度OB. 如果O’B’=1, A’B’=2, AB=274,求金字塔的高度OB.
B
O
C
A
A’
B’
O’
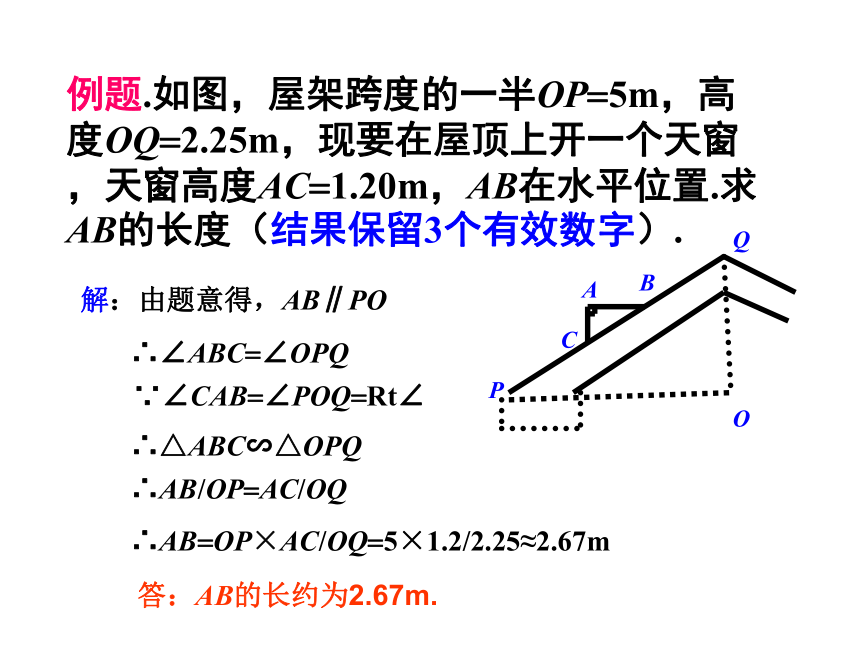
例题.如图,屋架跨度的一半OP=5m,高度OQ=2.25m,现要在屋顶上开一个天窗,天窗高度AC=1.20m,AB在水平位置.求AB的长度(结果保留3个有效数字).
P
O
Q
A
B
C
解:由题意得,AB∥PO
∴∠ABC=∠OPQ
∵∠CAB=∠POQ=Rt∠
∴△ABC∽△OPQ
∴AB/OP=AC/OQ
∴AB=OP×AC/OQ=5×1.2/2.25≈2.67m
答:AB的长约为2.67m.
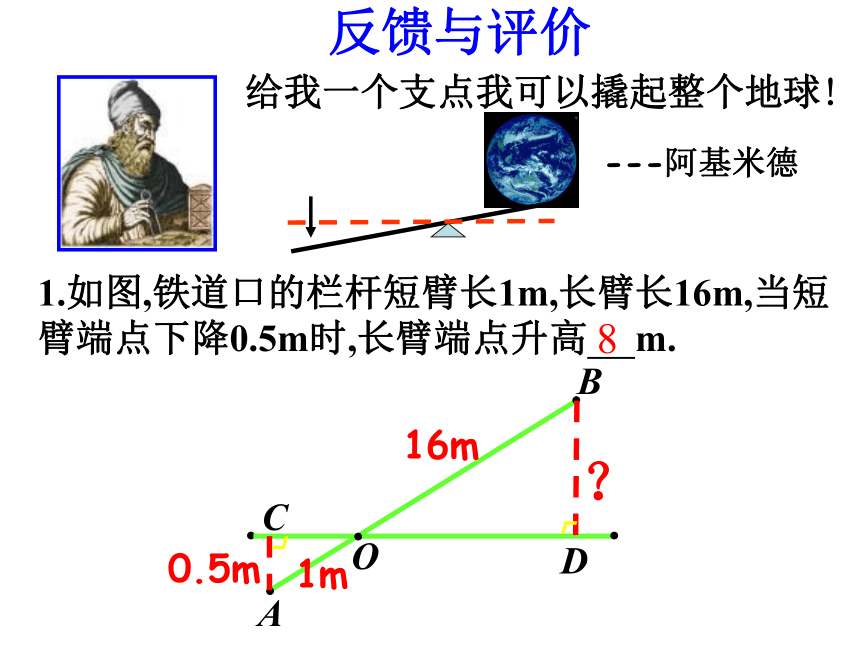
1.如图,铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高 m.
O
B
D
C
A
┏
┛
1m
16m
0.5m
8
给我一个支点我可以撬起整个地球!
---阿基米德
?
反馈与评价
2.某一时刻树的影长为8米,同一时刻身高为1.5米的人的影长为3米,则树高为 .
4米
3.如图:小明在打网球时,要使球恰好能打过网 ,而且落在离网5米的位置上,则拍击球的高度应为( ) .
5m
10m
0.9m
h
A、2.7米 B、1.8米
C、0.9米 D、 6米
A
如图,已知零件的外径为a,要求它的厚度x,需先求出内孔的直径AB,现用一个交叉卡钳(两条尺长AC和BD相等)去量,若OA:OC=OB:OD=n,且量得CD=b,求厚度x.
O
(分析:如图,要想求厚度x,根据条件可知,首先得求出内孔直径AB.而在图中可构造出相似形,通过相似形的性质,从而求出AB的长度.)
O
解:
∴△AOB∽△COD
∵AB=CD · n = nb
又∵CD=b
且∠AOB=∠COD
∵ OA:OC=OB:OD=n
∵ OA:OC=AB:CD=n
又∵x = ( a - AB )÷2
= ( a - nb )÷2
挑战自我
如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
N
M
Q
P
E
D
C
B
A
解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E.设正方形PQMN的边长为x毫米.
因为PN∥BC,所以△APN∽ △ABC
所以
AE
AD
=
PN
BC
因此 ,得 x=48(毫米).答:-------.
80-x
80
=
x
120
课堂小结:
一 、相似三角形的应用主要有如下两个方面
1 测高(不能直接使用皮尺或刻度尺量的)
2 测距(不能直接测量的两点间的距离)
、测高的方法
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长的比例”的原理解决
、测距的方法
测量不能到达两点间的距离,常构造相似三角形求解
解决实际问题时(如测高、测距),
一般有以下步骤:①审题 ②构建图形
③利用相似解决问题
怎样利用相似三角形的有关知识测量旗杆的高度
想一想
怎样测量旗杆的高度呢?
A
B
O
A′
B′
O′
求旗杆高度的方法:
旗杆的高度和影长组成的三角形
人身高和影长组成的三角形
因为旗杆的高度不能直接测量,我们可以利用
再利用相似三角形对应边成比例来求解.
相似于
B
B
C
A′
B′
C′
1、旗杆的高度是线段 ;旗杆的高度与它的影长组成什么三角形?( )这个三角形有没有哪条边可以直接测量?
温馨提示:
BC
△ABC
6m
2、人的高度与它的影长组成什么三角形?( )这个三角形有没有哪条边可以直接测量?
△A′B′C ′
3、 △ABC与△A′B′C ′ 有什么关系 试说明理由.
1.2m
1.6m
A
C
B
D
E
┐
┐
A
C
B
D
E
┐
┐
再见
复习提问:
我们已经学习相似三角形的性质有哪些?
1、相似三角形对应角相等.
2、相似三角形对应边成比例.
3、相似三角形的周长之比等于相似比;
4、相似三角形的面积之比等于相似比的平方.
5、相似三角形的对应高线、中线、角平分线之比等于相似比.
校园里有一棵大铁树,要测量树的高度,
你有什么方法?
把一小镜子放在离树(AB)8米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.8m,观察者目高CD=1.6m.这时树高多少?你能解决这个问题吗?
A
B
E
D
C
方法一
把长为2.40m的标杆CD直立在地面上,量出树的影长为2.80m,标杆的影长为1.47m.这时树高多少?你能解决这个问题吗? (精确到0.1m)
A
B
C
D
E
F
课内练习:
步枪在瞄准时的示意图如图,从眼睛到准星的距离OE为80cm,步枪上准星宽度AB为2mm,目标的正面宽度CD为50cm,求眼睛到目标的距离OF.
E
A
B
O
C
D
F
准星
A
B
古代一位数学家想出了一种测量金字塔高度的方法:为了测量金字塔的高度OB,先竖一根已知长度的木棒O’B’,比较棒子的影长A’B’与金字塔的影长AB,即可近似算出金字塔的高度OB. 如果O’B’=1, A’B’=2, AB=274,求金字塔的高度OB.
B
O
C
A
A’
B’
O’
例题.如图,屋架跨度的一半OP=5m,高度OQ=2.25m,现要在屋顶上开一个天窗,天窗高度AC=1.20m,AB在水平位置.求AB的长度(结果保留3个有效数字).
P
O
Q
A
B
C
解:由题意得,AB∥PO
∴∠ABC=∠OPQ
∵∠CAB=∠POQ=Rt∠
∴△ABC∽△OPQ
∴AB/OP=AC/OQ
∴AB=OP×AC/OQ=5×1.2/2.25≈2.67m
答:AB的长约为2.67m.
1.如图,铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高 m.
O
B
D
C
A
┏
┛
1m
16m
0.5m
8
给我一个支点我可以撬起整个地球!
---阿基米德
?
反馈与评价
2.某一时刻树的影长为8米,同一时刻身高为1.5米的人的影长为3米,则树高为 .
4米
3.如图:小明在打网球时,要使球恰好能打过网 ,而且落在离网5米的位置上,则拍击球的高度应为( ) .
5m
10m
0.9m
h
A、2.7米 B、1.8米
C、0.9米 D、 6米
A
如图,已知零件的外径为a,要求它的厚度x,需先求出内孔的直径AB,现用一个交叉卡钳(两条尺长AC和BD相等)去量,若OA:OC=OB:OD=n,且量得CD=b,求厚度x.
O
(分析:如图,要想求厚度x,根据条件可知,首先得求出内孔直径AB.而在图中可构造出相似形,通过相似形的性质,从而求出AB的长度.)
O
解:
∴△AOB∽△COD
∵AB=CD · n = nb
又∵CD=b
且∠AOB=∠COD
∵ OA:OC=OB:OD=n
∵ OA:OC=AB:CD=n
又∵x = ( a - AB )÷2
= ( a - nb )÷2
挑战自我
如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
N
M
Q
P
E
D
C
B
A
解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E.设正方形PQMN的边长为x毫米.
因为PN∥BC,所以△APN∽ △ABC
所以
AE
AD
=
PN
BC
因此 ,得 x=48(毫米).答:-------.
80-x
80
=
x
120
课堂小结:
一 、相似三角形的应用主要有如下两个方面
1 测高(不能直接使用皮尺或刻度尺量的)
2 测距(不能直接测量的两点间的距离)
、测高的方法
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长的比例”的原理解决
、测距的方法
测量不能到达两点间的距离,常构造相似三角形求解
解决实际问题时(如测高、测距),
一般有以下步骤:①审题 ②构建图形
③利用相似解决问题
怎样利用相似三角形的有关知识测量旗杆的高度
想一想
怎样测量旗杆的高度呢?
A
B
O
A′
B′
O′
求旗杆高度的方法:
旗杆的高度和影长组成的三角形
人身高和影长组成的三角形
因为旗杆的高度不能直接测量,我们可以利用
再利用相似三角形对应边成比例来求解.
相似于
B
B
C
A′
B′
C′
1、旗杆的高度是线段 ;旗杆的高度与它的影长组成什么三角形?( )这个三角形有没有哪条边可以直接测量?
温馨提示:
BC
△ABC
6m
2、人的高度与它的影长组成什么三角形?( )这个三角形有没有哪条边可以直接测量?
△A′B′C ′
3、 △ABC与△A′B′C ′ 有什么关系 试说明理由.
1.2m
1.6m
A
C
B
D
E
┐
┐
A
C
B
D
E
┐
┐
再见
