2021-2022学年度沪科版九年级数学上册课件 23.2解直角三角形及其应用(第2课时)(共14张PPT)
文档属性
| 名称 | 2021-2022学年度沪科版九年级数学上册课件 23.2解直角三角形及其应用(第2课时)(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览


文档简介
(共14张PPT)
第2课时
灯塔上发现在它的南偏东30°,距离500m的A处有一艘船,该船向正西方向航行,经过3分钟到达灯塔西北方向的B处,求这船的航速是每时多少千米( 取1.7)
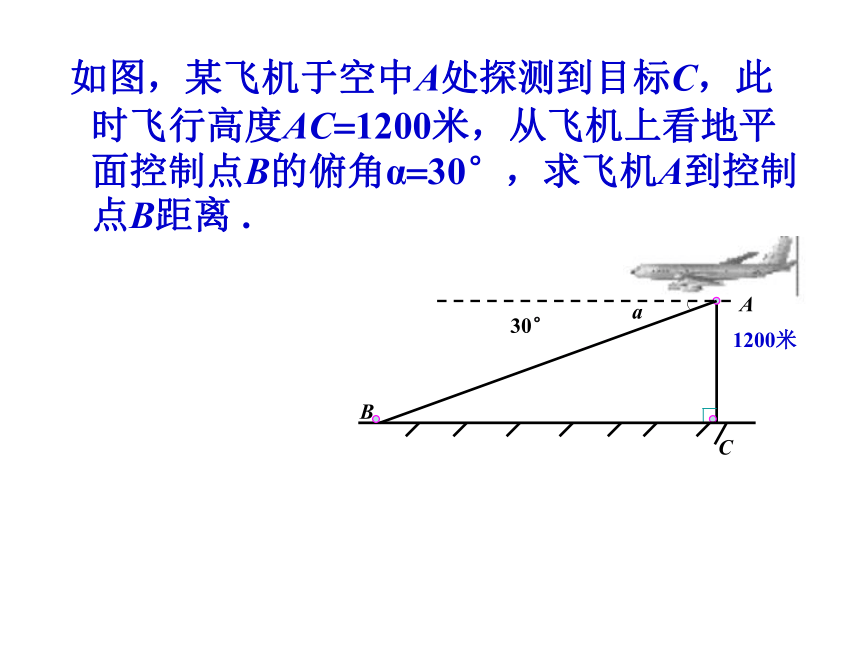
如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地平面控制点B的俯角α=30°,求飞机A到控制点B距离 .
A
︶
1200米
B
C
a
30°
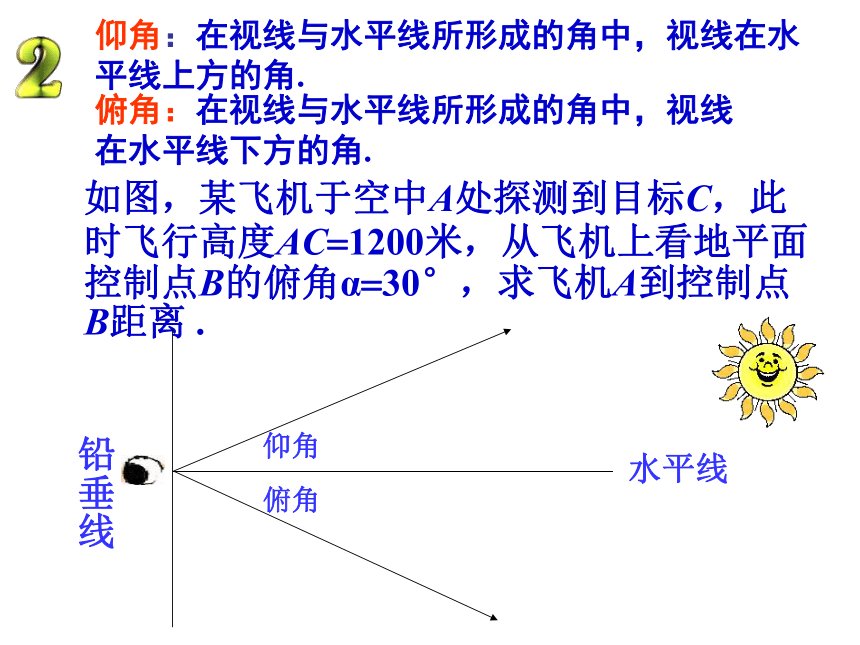
如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地平面控制点B的俯角α=30°,求飞机A到控制点B距离 .
仰角
俯角
铅垂线
水平线
仰角:在视线与水平线所形成的角中,视线在水平线上方的角.
俯角:在视线与水平线所形成的角中,视线在水平线下方的角.
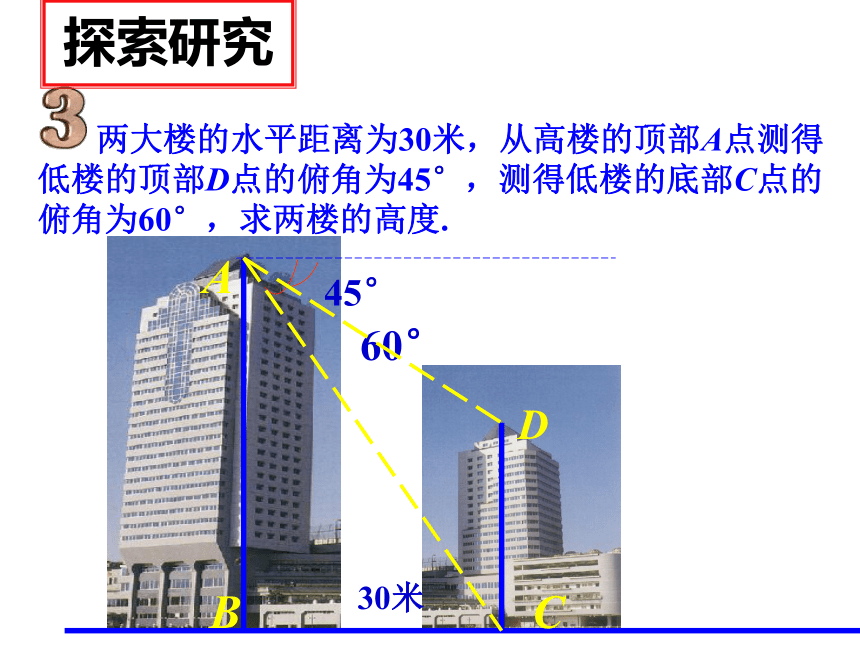
两大楼的水平距离为30米,从高楼的顶部A点测得低楼的顶部D点的俯角为45°,测得低楼的底部C点的俯角为60°,求两楼的高度.
A
D
B
C
30米
45°
60°
探索研究
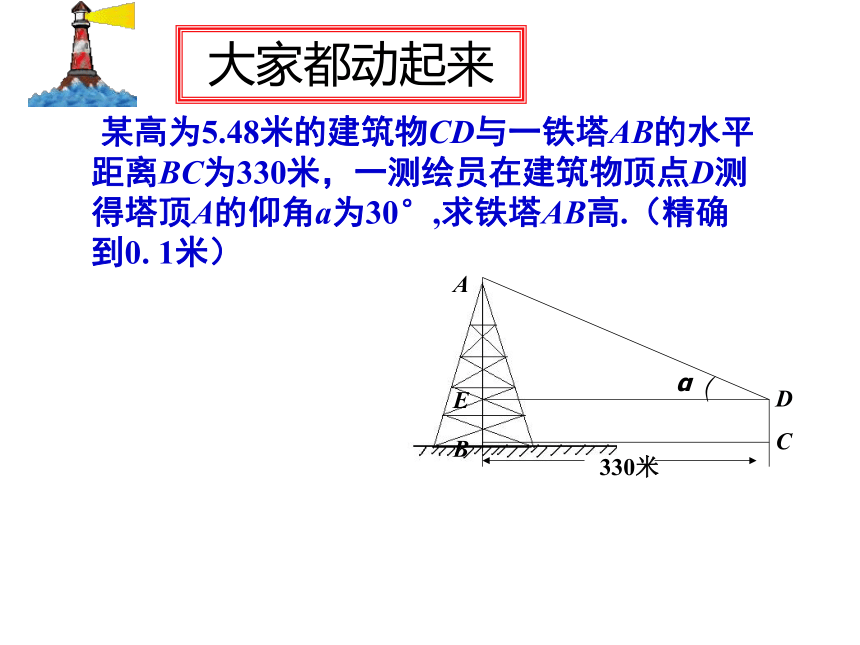
某高为5.48米的建筑物CD与一铁塔AB的水平距离BC为330米,一测绘员在建筑物顶点D测得塔顶A的仰角a为30°,求铁塔AB高.(精确到0. 1米)
330米
A
B
C
D
E
α
︶
大家都动起来
例 题
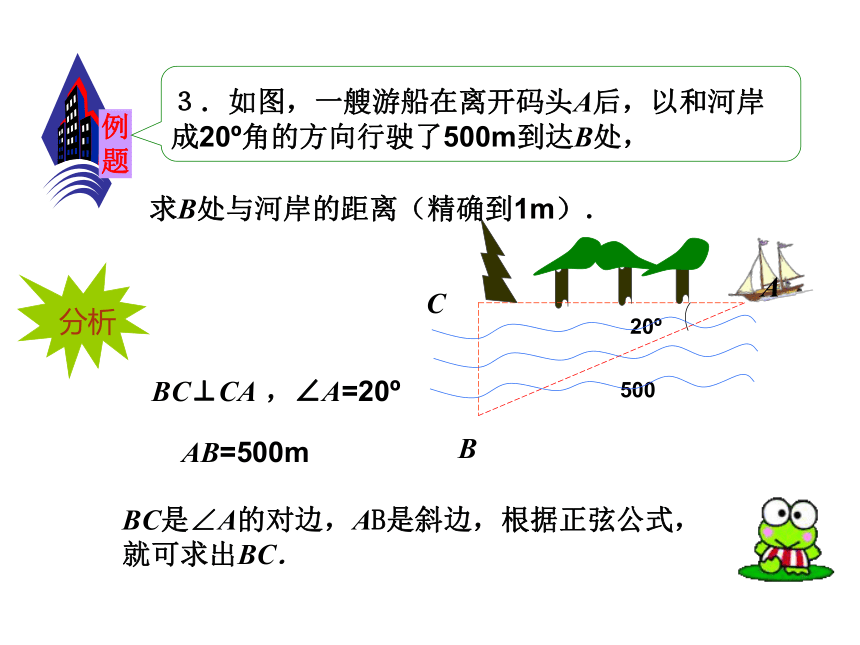
3.如图,一艘游船在离开码头A后,以和河岸成20 角的方向行驶了500m到达B处,
A
500
20
B
C
求B处与河岸的距离(精确到1m).
分析
BC⊥CA ,∠A=20
AB=500m
BC是∠A的对边,AB是斜边,根据正弦公式,就可求出BC.
解
从点B向河岸作垂线,垂足为C,
在 Rt△ABC 中,∠C= 90 , ∠A =20 ,AB=500m,
由于BC是∠A的对边,AB是斜边
C
B
A
500
20
答:B处与河岸的距离约为171m.
4.如图,在高为28.5m的楼顶平台D处,用仪器测得一路灯电线杆底部B的俯角为14 2',仪器高度为1.5m,求这根电线杆与这座楼的距离BC(精确到1m).
例 题
14 2'
B
D
A
C
分析
CD=28.5m, AD=1.5m ,
∠C=90 ,AC=28.5+1.5=30m
运用正切公式
即可求出BC.
在 Rt△ABC 中,∠C= 90 , ∠BAC =75 58',AC=30m,
由于BC是∠BAC的对边,AC是邻边,
答:这根电线杆与这座楼的距离约为120 m.
解
C
A
B
分析
由题意,△ABC是直角三角形, 其中∠C =90 ,∠A= 71 34',∠A所对的边BC=2400m,求 AC=?
北
东
一艘帆船航行到 B处时,灯塔A在船的北偏东71 34'的方向,
帆船从B处继续向正东方向航行2400m到达C处,此时灯塔A在船的正北方向.求C处和灯塔A的距离(精确到1m).
练 习
即可.
A
C
71 34'
B
在 Rt△ABC 中,∠C= 90 , ∠A =71 34',BC=2400m,
由于BC是∠A的对边,AC是邻边,
答:C处与灯塔A的距离约为120 m.
解
C
A
B
利用直角三角形中边与角的关系,解决实际问题,难点是分清角的对边.邻边,正确理解锐角的正弦.余弦.正切的概念.
2.在 Rt△ABC 中,∠C= 90 , ∠B = 28 32' ,a= 12.36cm,求∠A(精确到1’),c,b(精确到0.01cm).
基础
练习
小结
第2课时
灯塔上发现在它的南偏东30°,距离500m的A处有一艘船,该船向正西方向航行,经过3分钟到达灯塔西北方向的B处,求这船的航速是每时多少千米( 取1.7)
如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地平面控制点B的俯角α=30°,求飞机A到控制点B距离 .
A
︶
1200米
B
C
a
30°
如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地平面控制点B的俯角α=30°,求飞机A到控制点B距离 .
仰角
俯角
铅垂线
水平线
仰角:在视线与水平线所形成的角中,视线在水平线上方的角.
俯角:在视线与水平线所形成的角中,视线在水平线下方的角.
两大楼的水平距离为30米,从高楼的顶部A点测得低楼的顶部D点的俯角为45°,测得低楼的底部C点的俯角为60°,求两楼的高度.
A
D
B
C
30米
45°
60°
探索研究
某高为5.48米的建筑物CD与一铁塔AB的水平距离BC为330米,一测绘员在建筑物顶点D测得塔顶A的仰角a为30°,求铁塔AB高.(精确到0. 1米)
330米
A
B
C
D
E
α
︶
大家都动起来
例 题
3.如图,一艘游船在离开码头A后,以和河岸成20 角的方向行驶了500m到达B处,
A
500
20
B
C
求B处与河岸的距离(精确到1m).
分析
BC⊥CA ,∠A=20
AB=500m
BC是∠A的对边,AB是斜边,根据正弦公式,就可求出BC.
解
从点B向河岸作垂线,垂足为C,
在 Rt△ABC 中,∠C= 90 , ∠A =20 ,AB=500m,
由于BC是∠A的对边,AB是斜边
C
B
A
500
20
答:B处与河岸的距离约为171m.
4.如图,在高为28.5m的楼顶平台D处,用仪器测得一路灯电线杆底部B的俯角为14 2',仪器高度为1.5m,求这根电线杆与这座楼的距离BC(精确到1m).
例 题
14 2'
B
D
A
C
分析
CD=28.5m, AD=1.5m ,
∠C=90 ,AC=28.5+1.5=30m
运用正切公式
即可求出BC.
在 Rt△ABC 中,∠C= 90 , ∠BAC =75 58',AC=30m,
由于BC是∠BAC的对边,AC是邻边,
答:这根电线杆与这座楼的距离约为120 m.
解
C
A
B
分析
由题意,△ABC是直角三角形, 其中∠C =90 ,∠A= 71 34',∠A所对的边BC=2400m,求 AC=?
北
东
一艘帆船航行到 B处时,灯塔A在船的北偏东71 34'的方向,
帆船从B处继续向正东方向航行2400m到达C处,此时灯塔A在船的正北方向.求C处和灯塔A的距离(精确到1m).
练 习
即可.
A
C
71 34'
B
在 Rt△ABC 中,∠C= 90 , ∠A =71 34',BC=2400m,
由于BC是∠A的对边,AC是邻边,
答:C处与灯塔A的距离约为120 m.
解
C
A
B
利用直角三角形中边与角的关系,解决实际问题,难点是分清角的对边.邻边,正确理解锐角的正弦.余弦.正切的概念.
2.在 Rt△ABC 中,∠C= 90 , ∠B = 28 32' ,a= 12.36cm,求∠A(精确到1’),c,b(精确到0.01cm).
基础
练习
小结
