2021-2022学年度沪科版九年级数学上册课件 23.1.2 30°,45°,60°角的三角函数值(共17张PPT)
文档属性
| 名称 | 2021-2022学年度沪科版九年级数学上册课件 23.1.2 30°,45°,60°角的三角函数值(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1000.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览


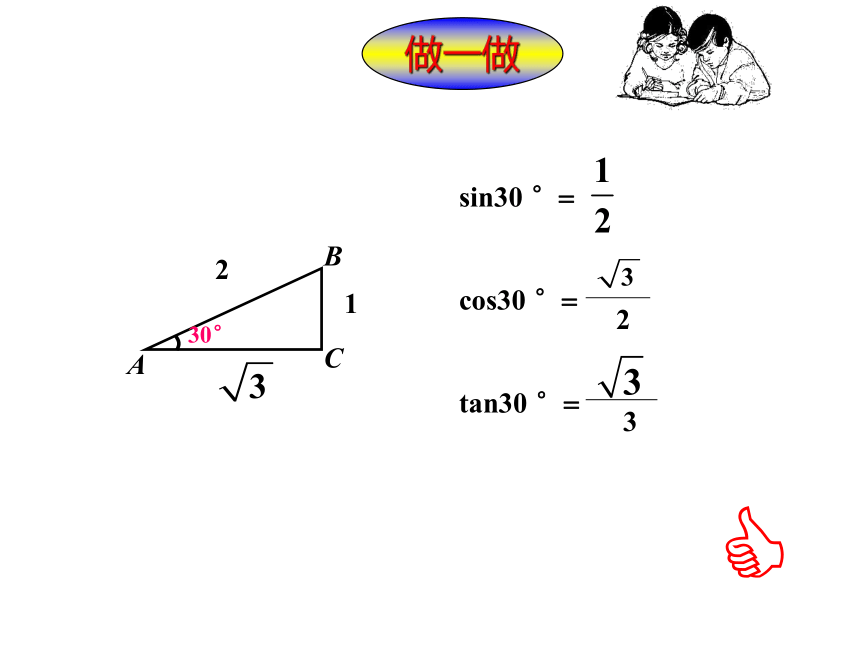

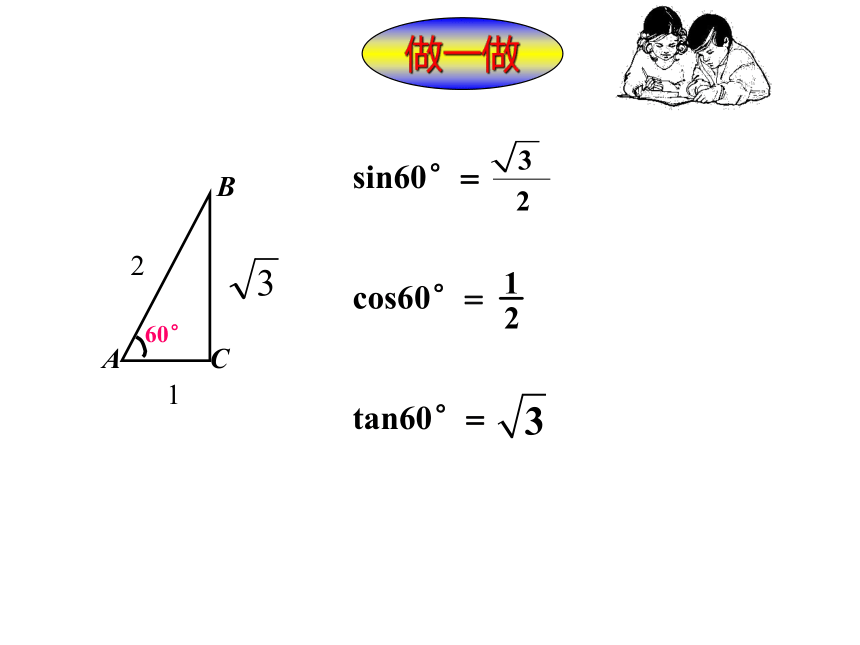
文档简介
(共17张PPT)
b
a
在直角三角形中,若一个锐角确定,那么这个角的对边,邻边和斜边之间的比值也随之确定.
锐角三角函数定义
直角三角形中边与角的关系:锐角三角函数.
b
A
B
C
a
┌
c
tan A=
tan B=
b
a
锐角A的正弦、余弦、和正切统称∠A的三角函数
脑中有“图”,心中有“式”
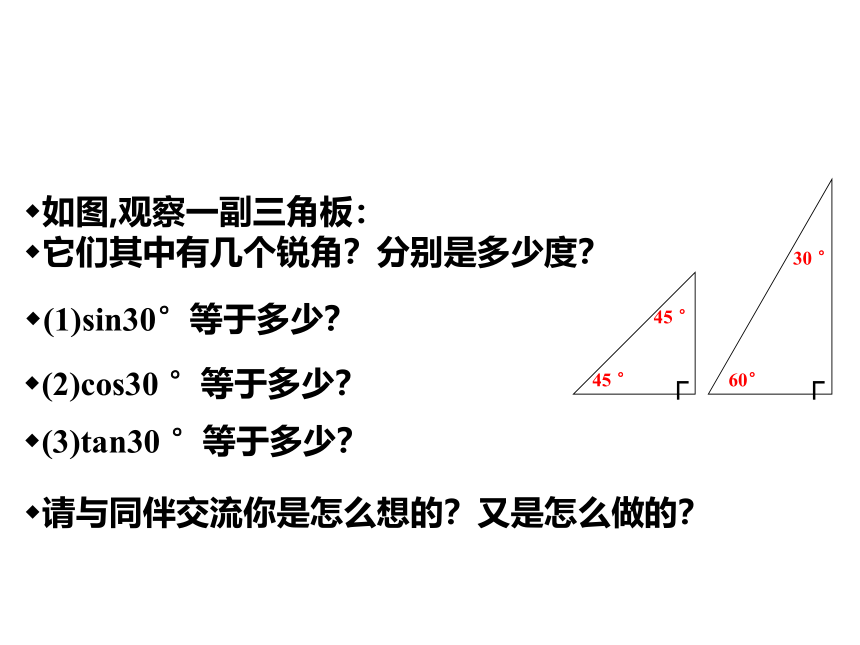
如图,观察一副三角板:
它们其中有几个锐角?分别是多少度?
(1)sin30°等于多少?
┌
┌
30 °
60°
45 °
45 °
(2)cos30 °等于多少?
(3)tan30 °等于多少?
请与同伴交流你是怎么想的?又是怎么做的?
做一做
A
B
C
30°
1
2
sin30 °=
cos30 °=
tan30 °=
2
3
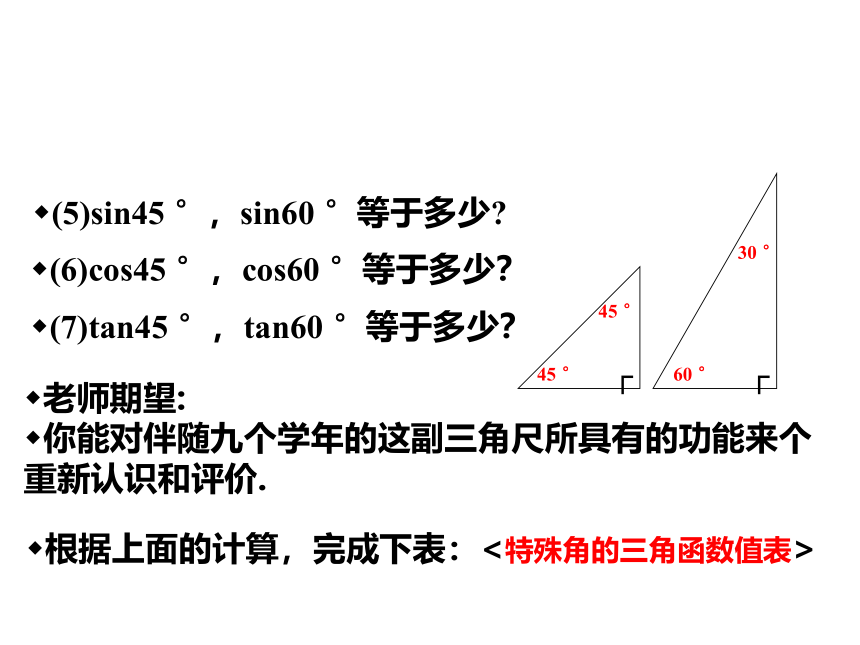
(5)sin45 °,sin60 °等于多少
(6)cos45 °,cos60 °等于多少?
(7)tan45 °,tan60 °等于多少?
┌
┌
30 °
60 °
45 °
45 °
根据上面的计算,完成下表:<特殊角的三角函数值表>
老师期望:
你能对伴随九个学年的这副三角尺所具有的功能来个重新认识和评价.
A
B
C
45°
1
1
sin45 °=
cos45°=
tan45°=
2
2
1
做一做
A
C
B
60°
1
2
sin60°=
cos60°=
tan60°=
2
做一做
特殊角的三角函数值表
要能记住有多好
三角函数
锐角α 正弦sinα 余弦cosα 正切tanα
30°
45°
60°
这张表还可以看出许多知识之间的内在联系
例1 计算:
(1)2sin30°-3cos60°;
(2)cos245°+tan60°·sin60°.
老师提示:
sin260°表示(sin60°)2,
cos260°表示(cos60°)2,其余类推.
(3)
(1)sin60°-cos45°;(2)cos60°+tan60°;
计算:
例2.一位同学的手臂长65cm,当他高举双臂时,指尖高出头顶35cm.问当他的手臂与水平成60°角时,指尖高出头顶多少cm(精确到0.1cm)?
老师期望:
sin2A+cos2A=1它反映了同角之间的三角函数的关系,且它更具有灵活变换的特点,若能予以掌握,则将有益于智力开发.
1.某商场有一自动扶梯,其倾斜角为30°,高为7m,扶梯的长度是多少?
2.如图,在Rt△ABC中,∠C=90°,∠A、∠B 、∠C的对边分别是a、b、c.
求证:sin2A+cos2A=1
b
A
B
C
a
┌
c
做一做
3、已知∠A为锐角,且cos A= ,
你能求出∠A的度数吗
2
讨论
独立
作业
4.如图,身高1.5m的小丽用一个两锐角分别是30°和60° 的三角尺测量一棵树的高度.已知她与树之间的距离为5m,那么这棵树大约有多高?
看图说话:
直角三角形三边的关系.
直角三角形两锐角的关系.
直角三角形边与角之间的关系.
特殊角30°,45°,60°角的三角函数值.
互余两角之间的三角函数关系.
同角之间的三角函数关系
b
A
B
C
a
┌
c
┌
┌
30 °
60 °
45 °
45 °
教学目标:
1.经历30°,45 °和60 °角的正弦、余弦和正切的探索过程,进一步体会三角函数的意义.
2.知道30 ° ,45 °和60 °角的三角函数值,并能进行于特殊锐角的三角函数值有关的计算,解决含有特殊锐角的直角三角形的计算问题.
重点和难点:
1.本节教学的重点是30 ° ,45 °和60 °角的三角函数值,以及综合运用这些特殊锐角的三角函数值和勾股定理等知识解决含有特殊锐角的直角三角形的计算问题.
2. 例题3的问题比较综合,解决时需要想象、构造直角三角形,是本节教学的难点.
结束寄语
在数学领域中,提出问题的艺术比解答的艺术更为重要.
b
a
在直角三角形中,若一个锐角确定,那么这个角的对边,邻边和斜边之间的比值也随之确定.
锐角三角函数定义
直角三角形中边与角的关系:锐角三角函数.
b
A
B
C
a
┌
c
tan A=
tan B=
b
a
锐角A的正弦、余弦、和正切统称∠A的三角函数
脑中有“图”,心中有“式”
如图,观察一副三角板:
它们其中有几个锐角?分别是多少度?
(1)sin30°等于多少?
┌
┌
30 °
60°
45 °
45 °
(2)cos30 °等于多少?
(3)tan30 °等于多少?
请与同伴交流你是怎么想的?又是怎么做的?
做一做
A
B
C
30°
1
2
sin30 °=
cos30 °=
tan30 °=
2
3
(5)sin45 °,sin60 °等于多少
(6)cos45 °,cos60 °等于多少?
(7)tan45 °,tan60 °等于多少?
┌
┌
30 °
60 °
45 °
45 °
根据上面的计算,完成下表:<特殊角的三角函数值表>
老师期望:
你能对伴随九个学年的这副三角尺所具有的功能来个重新认识和评价.
A
B
C
45°
1
1
sin45 °=
cos45°=
tan45°=
2
2
1
做一做
A
C
B
60°
1
2
sin60°=
cos60°=
tan60°=
2
做一做
特殊角的三角函数值表
要能记住有多好
三角函数
锐角α 正弦sinα 余弦cosα 正切tanα
30°
45°
60°
这张表还可以看出许多知识之间的内在联系
例1 计算:
(1)2sin30°-3cos60°;
(2)cos245°+tan60°·sin60°.
老师提示:
sin260°表示(sin60°)2,
cos260°表示(cos60°)2,其余类推.
(3)
(1)sin60°-cos45°;(2)cos60°+tan60°;
计算:
例2.一位同学的手臂长65cm,当他高举双臂时,指尖高出头顶35cm.问当他的手臂与水平成60°角时,指尖高出头顶多少cm(精确到0.1cm)?
老师期望:
sin2A+cos2A=1它反映了同角之间的三角函数的关系,且它更具有灵活变换的特点,若能予以掌握,则将有益于智力开发.
1.某商场有一自动扶梯,其倾斜角为30°,高为7m,扶梯的长度是多少?
2.如图,在Rt△ABC中,∠C=90°,∠A、∠B 、∠C的对边分别是a、b、c.
求证:sin2A+cos2A=1
b
A
B
C
a
┌
c
做一做
3、已知∠A为锐角,且cos A= ,
你能求出∠A的度数吗
2
讨论
独立
作业
4.如图,身高1.5m的小丽用一个两锐角分别是30°和60° 的三角尺测量一棵树的高度.已知她与树之间的距离为5m,那么这棵树大约有多高?
看图说话:
直角三角形三边的关系.
直角三角形两锐角的关系.
直角三角形边与角之间的关系.
特殊角30°,45°,60°角的三角函数值.
互余两角之间的三角函数关系.
同角之间的三角函数关系
b
A
B
C
a
┌
c
┌
┌
30 °
60 °
45 °
45 °
教学目标:
1.经历30°,45 °和60 °角的正弦、余弦和正切的探索过程,进一步体会三角函数的意义.
2.知道30 ° ,45 °和60 °角的三角函数值,并能进行于特殊锐角的三角函数值有关的计算,解决含有特殊锐角的直角三角形的计算问题.
重点和难点:
1.本节教学的重点是30 ° ,45 °和60 °角的三角函数值,以及综合运用这些特殊锐角的三角函数值和勾股定理等知识解决含有特殊锐角的直角三角形的计算问题.
2. 例题3的问题比较综合,解决时需要想象、构造直角三角形,是本节教学的难点.
结束寄语
在数学领域中,提出问题的艺术比解答的艺术更为重要.
