2021-2022学年度沪科版九年级数学上册课件 23.1.3一般锐角的三角函数值(第1课时)(共18张PPT)
文档属性
| 名称 | 2021-2022学年度沪科版九年级数学上册课件 23.1.3一般锐角的三角函数值(第1课时)(共18张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 10:48:57 | ||
图片预览



文档简介
(共18张PPT)
直角三角形两锐角的关系:两锐角互余 ∠A+∠B=90o.
直角三角的边角关系
直角三角形三边的关系:勾股定理 a2+b2=c2.
驶向胜利的彼岸
b
A
B
C
a
┌
c
互余两角之间的三角函数关系:
sin A=cos B
特殊角30o,45o,60o角的三角函数值.
直角三角形边与角之间的关系:锐角三角函数
同角之间的三角函数关系:
sin2A+cos2A=1.
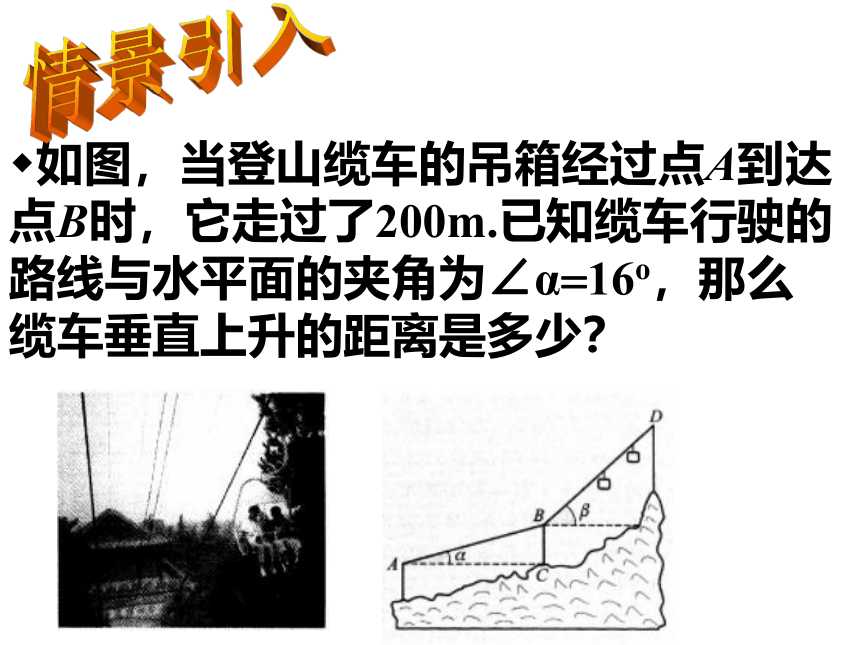
如图,当登山缆车的吊箱经过点A到达点B时,它走过了200m.已知缆车行驶的路线与水平面的夹角为∠α=16o,那么缆车垂直上升的距离是多少?
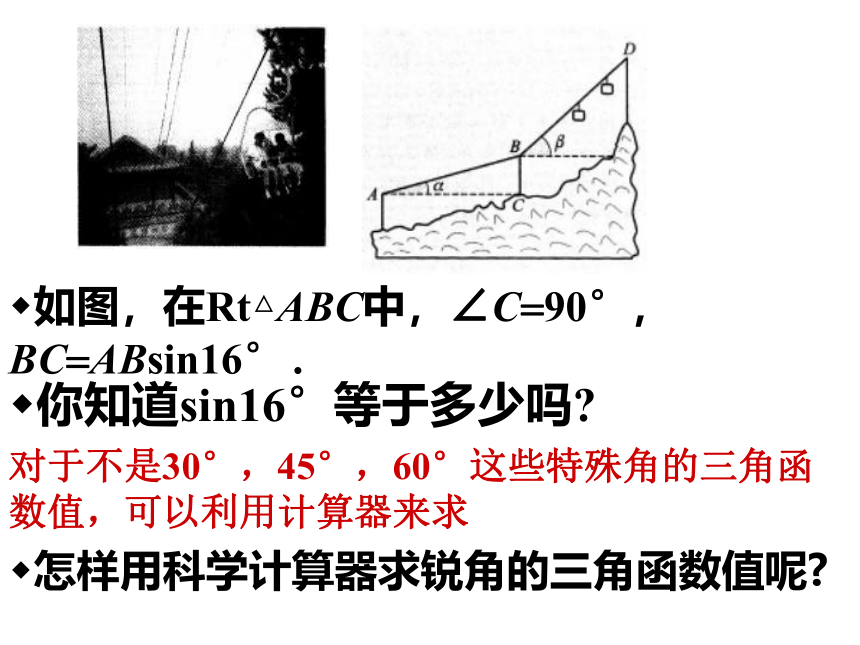
你知道sin16°等于多少吗
怎样用科学计算器求锐角的三角函数值呢
如图,在Rt△ABC中,∠C=90°, BC=ABsin16° .
对于不是30°,45°,60°这些特殊角的三角函数值,可以利用计算器来求
知识在于积累
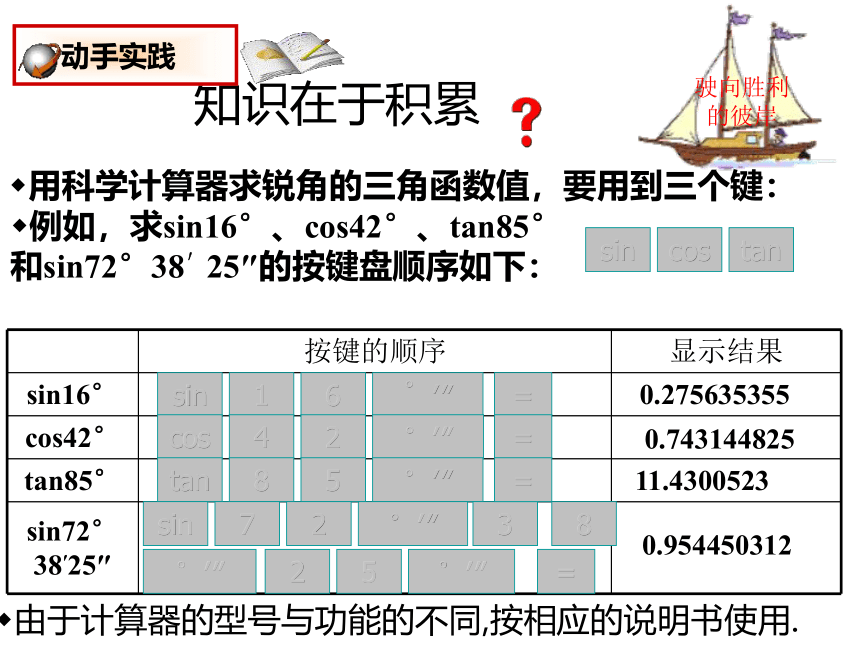
用科学计算器求锐角的三角函数值,要用到三个键:
动手实践
例如,求sin16°、cos42°、tan85°和sin72°38′25″的按键盘顺序如下:
驶向胜利的彼岸
由于计算器的型号与功能的不同,按相应的说明书使用.
sin
cos
tan
按键的顺序 显示结果
sin16°
cos42°
tan85°
sin72° 38′25″
sin
1
6
°′″
0.275635355
cos
4
2
°′″
0.743144825
tan
8
5
°′″
11.4300523
sin
7
2
°′″
3
8
°′″
2
5
°′″
0.954450312
=
=
=
=
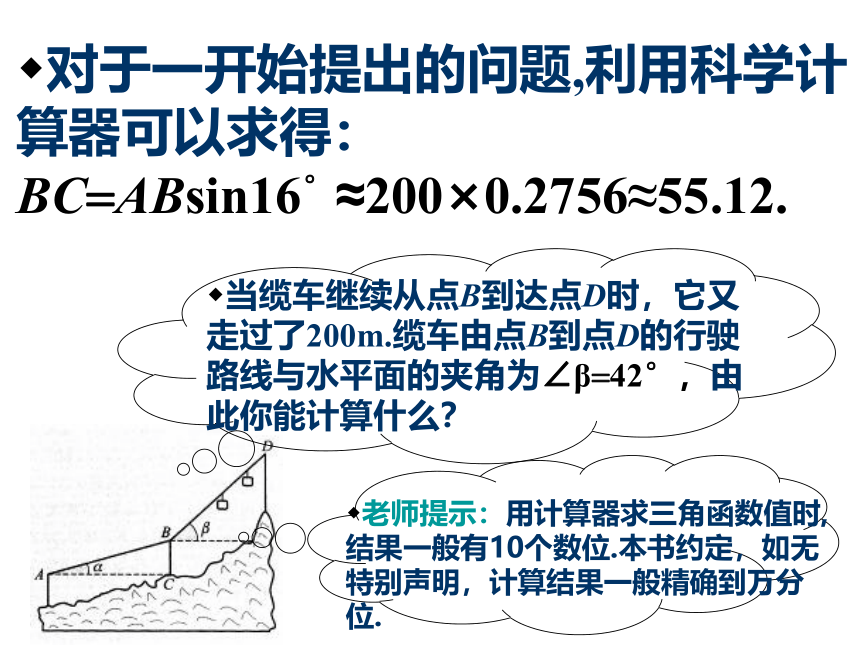
对于一开始提出的问题,利用科学计算器可以求得: BC=ABsin16°≈200×0.2756≈55.12.
当缆车继续从点B到达点D时,它又走过了200m.缆车由点B到点D的行驶路线与水平面的夹角为∠β=42°,由此你能计算什么?
老师提示:用计算器求三角函数值时,结果一般有10个数位.本书约定,如无特别声明,计算结果一般精确到万分位.
求下列各函数值,并把它们按从小到大的顺序用“<”连接:
(2)cos27°12′,cos85°,cos63°36′15″, cos54°23′,cos38°39′52
小结:sinα,tanα随着锐角α的增大而增大;
cosα随着锐角α的增大而减小.
问:当α为锐角时,各类三角函数值随着角度的
增大而做怎样的变化
(1)
例1、如图,在Rt△ABC中, ∠C =90 ° .已知AB=12cm,∠ A=35 °,求△ABC的周长和面
积(周长精确到0.1cm,面积保留3个是效数字).
B
C
A
变式:在△ABC中,已知AB=12cm,AC=10cm
∠ A=35 °,求△ABC 的周长和面积(周长精确到0.1cm,面积保留3个是效数字).
模型: △ABC 的面积=1/2AC AB sin ∠ A
行家看“门道”
1 用计算器求下列各式的值:
(1)sin56°,(2) sin15°49′,(3)cos20°,(4)tan29°,
(5)tan44°59′59″,(6)sin15°+cos61°+tan76°.
随堂练习
驶向胜利的彼岸
怎样解答
2 一个人由山底爬到山顶,需先爬40°的山坡300m,再爬30° 的山坡100m,求山高(结果精确到0.01m).
3.求图中避雷针的长度(结果精确到0.01m).
知识的运用
怎样做?
驶向胜利的彼岸
4 如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.
老师期望:
体会这两个图形的“模型”作用.将会助你登上希望的峰顶.
A
B
C
45°
30°
4cm
5 如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.
A
B
C
45°
30°
4cm
D
┌
2模型:
真知在实践中诞生
6 如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.
驶向胜利的彼岸
咋办
老师期望:
你能得到作为“模型”的它给你带来的成功.
7 如图,根据图中已知数据,求AD.
A
B
C
α
β
a
A
B
C
β
α
a
D
┌
25°
太阳光
D
C
A
B
新楼
住宅楼
某居民小区有一朝向为正南方向的居民楼,该居民楼的一楼是高6米的小区超市,超市以上是居民住房.在该楼的前面要盖一栋高20米的新楼.当冬季正午的阳光与水平线的夹角为25°时.问:若要使超市采光不受影响,两楼应相距多少米?
25°
太阳光
D
C
A
B
新楼
住宅楼
某居民小区有一朝向为正南方向的居民楼,该居民楼的一楼是高6米的小区超市,超市以上是居民住房.在该楼的前面要盖一栋高20米的新楼.当冬季正午的阳光与水平线的夹角为25°时.
问:若新楼的影子恰好落在超市1米高的窗台处,两楼应相距多少米?
F
E
真知在实践中诞生
图中的螺旋形由一系列直角三角形组成.每个三角形都以点O为一顶点.
(1)求∠A0OA1,∠A1OA2,∠A2OA3的大小.
(2)已知∠An-1OAn是一个小于20°的角,求n的值.
A
B
C
“斜而未倒”
BC=5.2m
AB=54.5m
意大利的伟大科学家伽俐略,曾在斜塔的顶层做过自由落体运动的实验 .
α
这节课你有哪些收获
结束寄语
一个人就好象一个分数,他的实际才干就好比分子,而他对自己的估计就好比分母,分母越大,则分数的值就越小.
——托尔斯泰
下课了!
再见
直角三角形两锐角的关系:两锐角互余 ∠A+∠B=90o.
直角三角的边角关系
直角三角形三边的关系:勾股定理 a2+b2=c2.
驶向胜利的彼岸
b
A
B
C
a
┌
c
互余两角之间的三角函数关系:
sin A=cos B
特殊角30o,45o,60o角的三角函数值.
直角三角形边与角之间的关系:锐角三角函数
同角之间的三角函数关系:
sin2A+cos2A=1.
如图,当登山缆车的吊箱经过点A到达点B时,它走过了200m.已知缆车行驶的路线与水平面的夹角为∠α=16o,那么缆车垂直上升的距离是多少?
你知道sin16°等于多少吗
怎样用科学计算器求锐角的三角函数值呢
如图,在Rt△ABC中,∠C=90°, BC=ABsin16° .
对于不是30°,45°,60°这些特殊角的三角函数值,可以利用计算器来求
知识在于积累
用科学计算器求锐角的三角函数值,要用到三个键:
动手实践
例如,求sin16°、cos42°、tan85°和sin72°38′25″的按键盘顺序如下:
驶向胜利的彼岸
由于计算器的型号与功能的不同,按相应的说明书使用.
sin
cos
tan
按键的顺序 显示结果
sin16°
cos42°
tan85°
sin72° 38′25″
sin
1
6
°′″
0.275635355
cos
4
2
°′″
0.743144825
tan
8
5
°′″
11.4300523
sin
7
2
°′″
3
8
°′″
2
5
°′″
0.954450312
=
=
=
=
对于一开始提出的问题,利用科学计算器可以求得: BC=ABsin16°≈200×0.2756≈55.12.
当缆车继续从点B到达点D时,它又走过了200m.缆车由点B到点D的行驶路线与水平面的夹角为∠β=42°,由此你能计算什么?
老师提示:用计算器求三角函数值时,结果一般有10个数位.本书约定,如无特别声明,计算结果一般精确到万分位.
求下列各函数值,并把它们按从小到大的顺序用“<”连接:
(2)cos27°12′,cos85°,cos63°36′15″, cos54°23′,cos38°39′52
小结:sinα,tanα随着锐角α的增大而增大;
cosα随着锐角α的增大而减小.
问:当α为锐角时,各类三角函数值随着角度的
增大而做怎样的变化
(1)
例1、如图,在Rt△ABC中, ∠C =90 ° .已知AB=12cm,∠ A=35 °,求△ABC的周长和面
积(周长精确到0.1cm,面积保留3个是效数字).
B
C
A
变式:在△ABC中,已知AB=12cm,AC=10cm
∠ A=35 °,求△ABC 的周长和面积(周长精确到0.1cm,面积保留3个是效数字).
模型: △ABC 的面积=1/2AC AB sin ∠ A
行家看“门道”
1 用计算器求下列各式的值:
(1)sin56°,(2) sin15°49′,(3)cos20°,(4)tan29°,
(5)tan44°59′59″,(6)sin15°+cos61°+tan76°.
随堂练习
驶向胜利的彼岸
怎样解答
2 一个人由山底爬到山顶,需先爬40°的山坡300m,再爬30° 的山坡100m,求山高(结果精确到0.01m).
3.求图中避雷针的长度(结果精确到0.01m).
知识的运用
怎样做?
驶向胜利的彼岸
4 如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.
老师期望:
体会这两个图形的“模型”作用.将会助你登上希望的峰顶.
A
B
C
45°
30°
4cm
5 如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.
A
B
C
45°
30°
4cm
D
┌
2模型:
真知在实践中诞生
6 如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.
驶向胜利的彼岸
咋办
老师期望:
你能得到作为“模型”的它给你带来的成功.
7 如图,根据图中已知数据,求AD.
A
B
C
α
β
a
A
B
C
β
α
a
D
┌
25°
太阳光
D
C
A
B
新楼
住宅楼
某居民小区有一朝向为正南方向的居民楼,该居民楼的一楼是高6米的小区超市,超市以上是居民住房.在该楼的前面要盖一栋高20米的新楼.当冬季正午的阳光与水平线的夹角为25°时.问:若要使超市采光不受影响,两楼应相距多少米?
25°
太阳光
D
C
A
B
新楼
住宅楼
某居民小区有一朝向为正南方向的居民楼,该居民楼的一楼是高6米的小区超市,超市以上是居民住房.在该楼的前面要盖一栋高20米的新楼.当冬季正午的阳光与水平线的夹角为25°时.
问:若新楼的影子恰好落在超市1米高的窗台处,两楼应相距多少米?
F
E
真知在实践中诞生
图中的螺旋形由一系列直角三角形组成.每个三角形都以点O为一顶点.
(1)求∠A0OA1,∠A1OA2,∠A2OA3的大小.
(2)已知∠An-1OAn是一个小于20°的角,求n的值.
A
B
C
“斜而未倒”
BC=5.2m
AB=54.5m
意大利的伟大科学家伽俐略,曾在斜塔的顶层做过自由落体运动的实验 .
α
这节课你有哪些收获
结束寄语
一个人就好象一个分数,他的实际才干就好比分子,而他对自己的估计就好比分母,分母越大,则分数的值就越小.
——托尔斯泰
下课了!
再见
