2021-2022学年度沪科版九年级数学下册课件 24.3圆周角(第1课时)(共22张PPT)
文档属性
| 名称 | 2021-2022学年度沪科版九年级数学下册课件 24.3圆周角(第1课时)(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览



文档简介
(共22张PPT)
●O
E
F
A
B
C
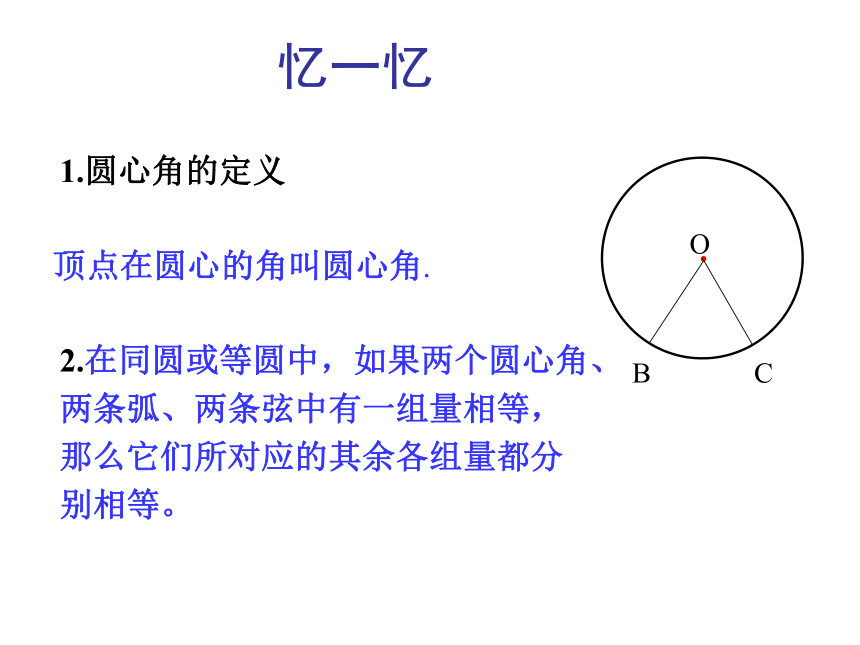
1.圆心角的定义
顶点在圆心的角叫圆心角.
2.在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
.
O
B
C
忆一忆
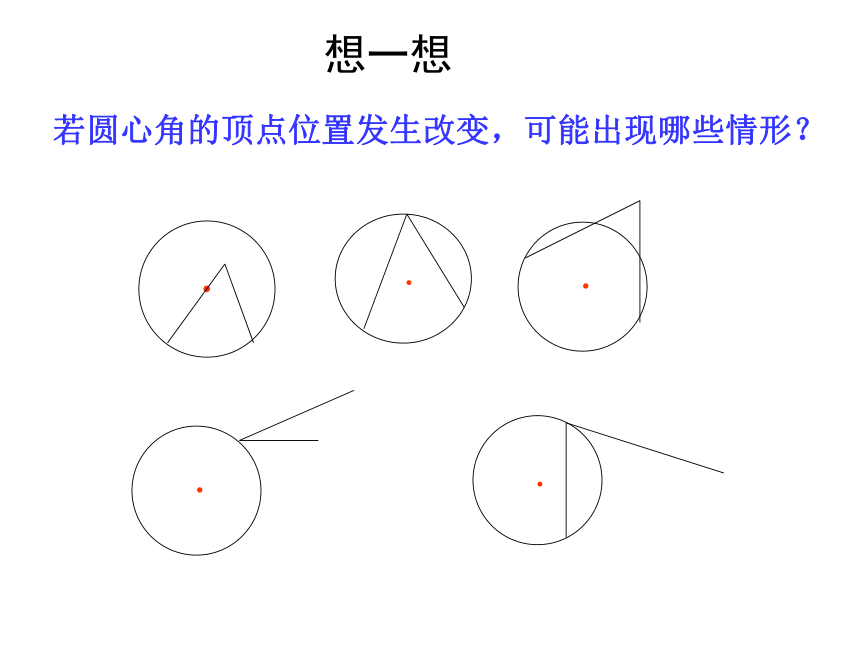
若圆心角的顶点位置发生改变,可能出现哪些情形?
·
·
·
·
·
想一想
在射门游戏中,球员射中球门的难易与它所处的位置B对球门AC的张角( ∠ABC )有关.
思考:图中的∠ABC的顶点各在圆的什么位置?∠ABC的两边和圆是什么关系?
A
B
C
D
E
B
A
C
A
B
C
D
E
●O
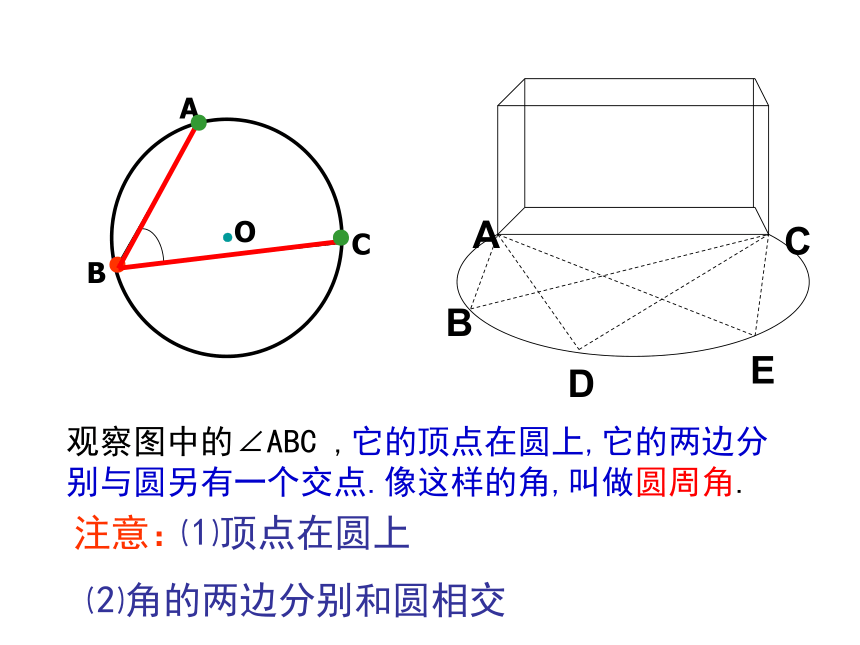
观察图中的∠ABC ,它的顶点在圆上,它的两边分别与圆另有一个交点.像这样的角,叫做圆周角.
⑵角的两边分别和圆相交
●
注意:
⑴顶点在圆上
●
●
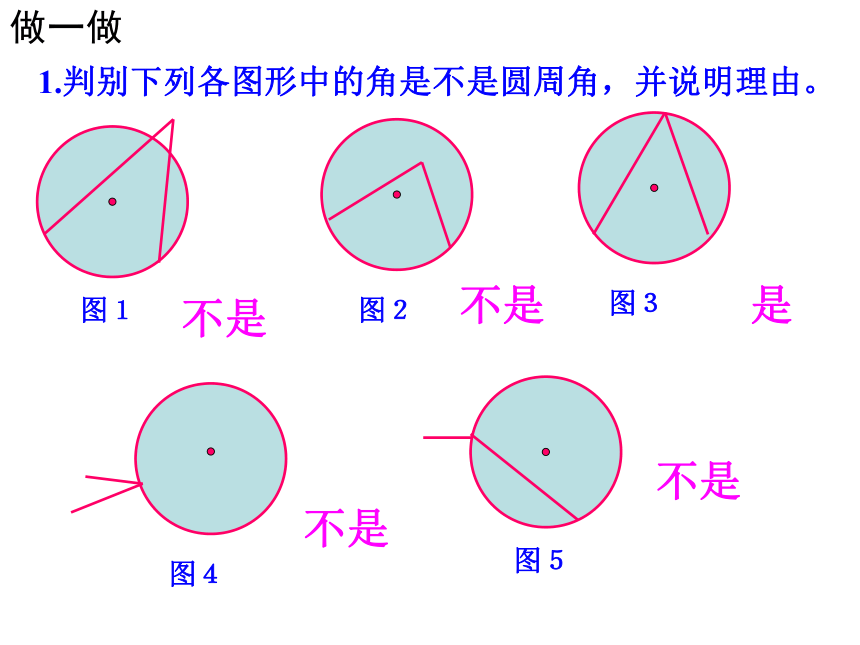
1.判别下列各图形中的角是不是圆周角,并说明理由。
不是
不是
是
不是
不是
图1
图2
图3
图4
图5
做一做
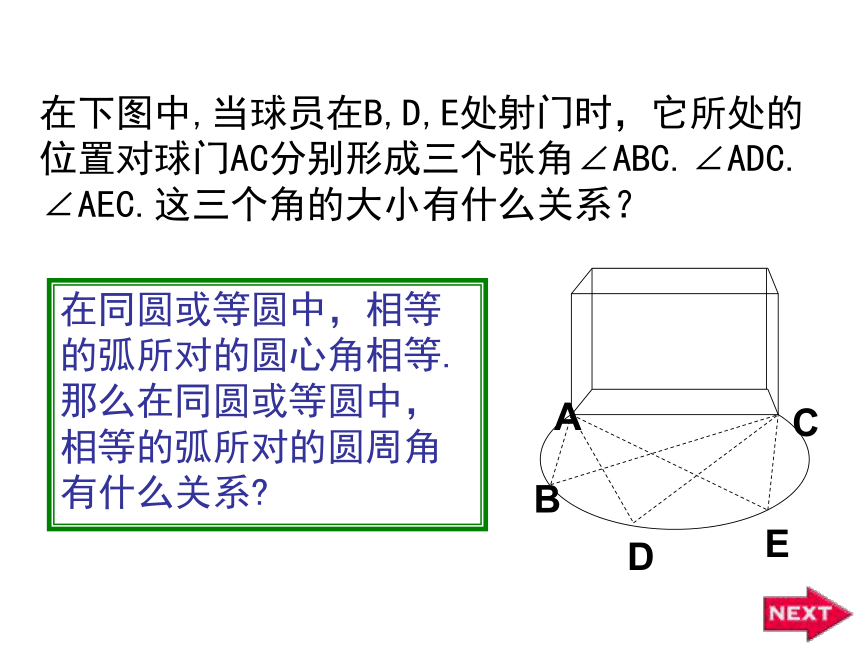
在下图中,当球员在B,D,E处射门时,它所处的位置对球门AC分别形成三个张角∠ABC.∠ADC. ∠AEC.这三个角的大小有什么关系?
在同圆或等圆中,相等的弧所对的圆心角相等.那么在同圆或等圆中,相等的弧所对的圆周角有什么关系
A
B
C
D
E
类比圆心角探知圆周角
在同圆或等圆中,相等的弧所对的圆心角相等.
在同圆或等圆中,相等的弧所对的圆周角有什么关系?
A
B
C
●O
E
F
我们先来研究一条弧所对的圆周角和圆心角的关系
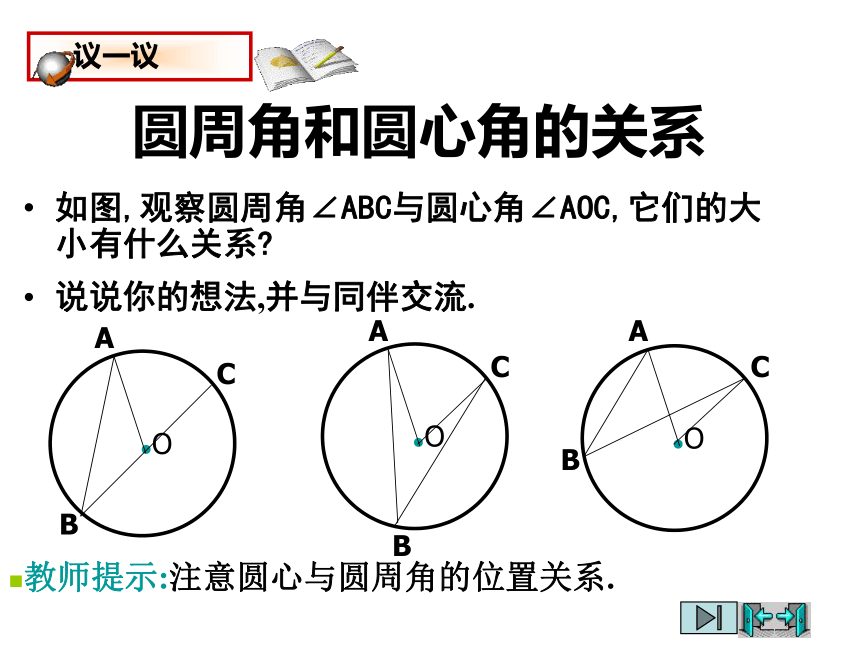
圆周角和圆心角的关系
如图,观察圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系
说说你的想法,并与同伴交流.
议一议
教师提示:注意圆心与圆周角的位置关系.
●O
A
B
C
●O
A
B
C
●O
A
B
C
如图,在⊙O中,观察圆周角∠ABC 与圆心角∠AOC ,它们的大小有什么关系
O
A
C
B
议一议
即∠ABC的一边BC过圆心O.
∵ ∠AOC 是△ABO的外角,
∴ ∠AOC = ∠ABO+ ∠BAO.
∵OA=OB
∴ ∠ABO = ∠BAO
∴ ∠AOC =2 ∠ABO
O
A
C
B
你能写出这个命题吗
一条弧所对的圆周角等于它所对的圆心角的一半.
①.首先考虑一种特殊情况:
试一试
②当圆心(O)在圆周角(∠ABC)的内部时,圆周角
∠ABC与圆心角∠AOC的大小关系会怎样
提示:能否转化为①的情况
过点B作直径BD.由①可得:
∠ABD = ∠AOD,∠CBD = ∠COD,
∴ ∠ABC = ∠AOC.
你能写出这个命题吗
●O
A
B
C
D
一条弧所对的圆周角等于它所对的圆心角的一半.
试一试
③当圆心(O)在圆周角(∠ABC)的外部时,圆周
角∠ABC与圆心角∠AOC的大小关系会怎样
提示:能否也转化为①的情况
过点B作直径BD.由①可得:
∠ABD = ∠AOD,∠CBD = ∠COD,
∴ ∠ABC = ∠AOC.
你能写出这个命题吗
●O
A
B
C
一条弧所对的圆周角等于
它所对的圆心角的一半.
D
试一试
圆周角定理
同一条弧所对的圆周角等
于它所对的圆心角的一半
●O
A
B
C
●O
A
B
C
●O
A
B
C
·
·
·
·
100°
A
O
20°
O
90°
A
B
A
B
B
C
O
B
A
C
C
(1)
(2)
(3)
(4)
AB为直径,求∠ACB
求∠AOB
求∠AOB
求∠A
做一做
2、如图 .已知圆心角∠AOB的度数为100°.求圆周角∠ACB的度数.
A
O
B
C
做一做
驶向胜利的彼岸
3.如图(1),在⊙O中,∠BAC=50°,求∠C的大小.
猜一猜
4.如图(2),在⊙O中,∠B,∠D,∠E的大小有什么关系 为什么
●O
●O
C
A
B
D
B
A
C
D
E
(1) (2)
做一做
2.如图.在⊙O中.∠BOC=50°,求∠BAC 的大小.
B
O
C
A
1.举出生活中含有圆周角的例子.
随堂练习
解: ∠A= ∠BOC = 25°.
习 题
证明:
∠ACB= ∠AOB
1
2
∠BAC= ∠BOC
2
∠AOB=2∠BOC
A
O
B
C
∠ACB=2∠BAC
1
规律:解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理
AB所对圆周角是∠ACB, 圆心角是∠AOB. 则∠ACB= ∠AOB.
BC所对圆周角是∠ BAC , 圆心角是∠BOC, 则∠ BAC= ∠BOC
1
___
分析:
2
再 见
●O
E
F
A
B
C
1.圆心角的定义
顶点在圆心的角叫圆心角.
2.在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
.
O
B
C
忆一忆
若圆心角的顶点位置发生改变,可能出现哪些情形?
·
·
·
·
·
想一想
在射门游戏中,球员射中球门的难易与它所处的位置B对球门AC的张角( ∠ABC )有关.
思考:图中的∠ABC的顶点各在圆的什么位置?∠ABC的两边和圆是什么关系?
A
B
C
D
E
B
A
C
A
B
C
D
E
●O
观察图中的∠ABC ,它的顶点在圆上,它的两边分别与圆另有一个交点.像这样的角,叫做圆周角.
⑵角的两边分别和圆相交
●
注意:
⑴顶点在圆上
●
●
1.判别下列各图形中的角是不是圆周角,并说明理由。
不是
不是
是
不是
不是
图1
图2
图3
图4
图5
做一做
在下图中,当球员在B,D,E处射门时,它所处的位置对球门AC分别形成三个张角∠ABC.∠ADC. ∠AEC.这三个角的大小有什么关系?
在同圆或等圆中,相等的弧所对的圆心角相等.那么在同圆或等圆中,相等的弧所对的圆周角有什么关系
A
B
C
D
E
类比圆心角探知圆周角
在同圆或等圆中,相等的弧所对的圆心角相等.
在同圆或等圆中,相等的弧所对的圆周角有什么关系?
A
B
C
●O
E
F
我们先来研究一条弧所对的圆周角和圆心角的关系
圆周角和圆心角的关系
如图,观察圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系
说说你的想法,并与同伴交流.
议一议
教师提示:注意圆心与圆周角的位置关系.
●O
A
B
C
●O
A
B
C
●O
A
B
C
如图,在⊙O中,观察圆周角∠ABC 与圆心角∠AOC ,它们的大小有什么关系
O
A
C
B
议一议
即∠ABC的一边BC过圆心O.
∵ ∠AOC 是△ABO的外角,
∴ ∠AOC = ∠ABO+ ∠BAO.
∵OA=OB
∴ ∠ABO = ∠BAO
∴ ∠AOC =2 ∠ABO
O
A
C
B
你能写出这个命题吗
一条弧所对的圆周角等于它所对的圆心角的一半.
①.首先考虑一种特殊情况:
试一试
②当圆心(O)在圆周角(∠ABC)的内部时,圆周角
∠ABC与圆心角∠AOC的大小关系会怎样
提示:能否转化为①的情况
过点B作直径BD.由①可得:
∠ABD = ∠AOD,∠CBD = ∠COD,
∴ ∠ABC = ∠AOC.
你能写出这个命题吗
●O
A
B
C
D
一条弧所对的圆周角等于它所对的圆心角的一半.
试一试
③当圆心(O)在圆周角(∠ABC)的外部时,圆周
角∠ABC与圆心角∠AOC的大小关系会怎样
提示:能否也转化为①的情况
过点B作直径BD.由①可得:
∠ABD = ∠AOD,∠CBD = ∠COD,
∴ ∠ABC = ∠AOC.
你能写出这个命题吗
●O
A
B
C
一条弧所对的圆周角等于
它所对的圆心角的一半.
D
试一试
圆周角定理
同一条弧所对的圆周角等
于它所对的圆心角的一半
●O
A
B
C
●O
A
B
C
●O
A
B
C
·
·
·
·
100°
A
O
20°
O
90°
A
B
A
B
B
C
O
B
A
C
C
(1)
(2)
(3)
(4)
AB为直径,求∠ACB
求∠AOB
求∠AOB
求∠A
做一做
2、如图 .已知圆心角∠AOB的度数为100°.求圆周角∠ACB的度数.
A
O
B
C
做一做
驶向胜利的彼岸
3.如图(1),在⊙O中,∠BAC=50°,求∠C的大小.
猜一猜
4.如图(2),在⊙O中,∠B,∠D,∠E的大小有什么关系 为什么
●O
●O
C
A
B
D
B
A
C
D
E
(1) (2)
做一做
2.如图.在⊙O中.∠BOC=50°,求∠BAC 的大小.
B
O
C
A
1.举出生活中含有圆周角的例子.
随堂练习
解: ∠A= ∠BOC = 25°.
习 题
证明:
∠ACB= ∠AOB
1
2
∠BAC= ∠BOC
2
∠AOB=2∠BOC
A
O
B
C
∠ACB=2∠BAC
1
规律:解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理
AB所对圆周角是∠ACB, 圆心角是∠AOB. 则∠ACB= ∠AOB.
BC所对圆周角是∠ BAC , 圆心角是∠BOC, 则∠ BAC= ∠BOC
1
___
分析:
2
再 见
