2021-2022学年度沪科版九年级数学下册课件 24.3圆周角(第2课时)(共17张PPT)
文档属性
| 名称 | 2021-2022学年度沪科版九年级数学下册课件 24.3圆周角(第2课时)(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 914.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
●O
B
A
C
D
E
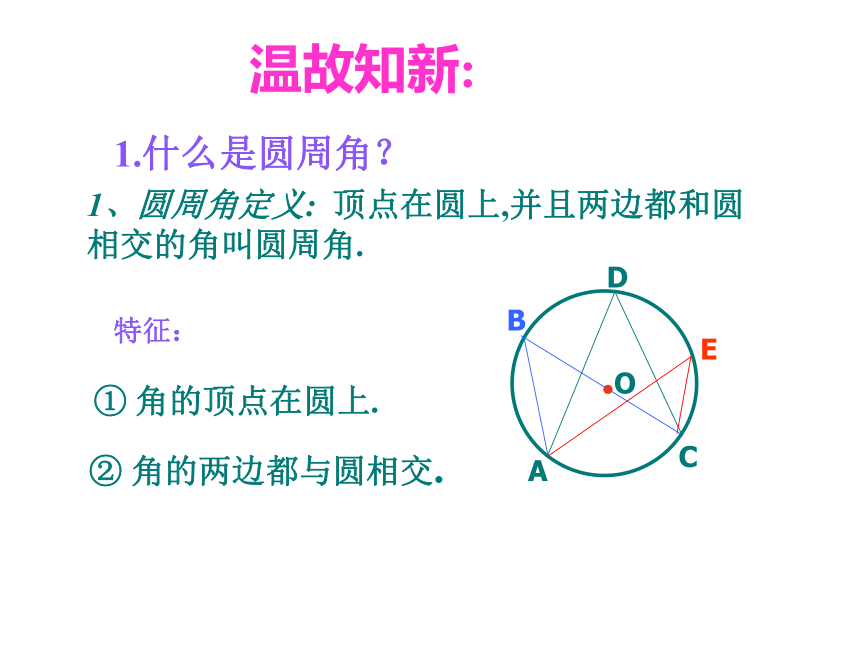
特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
1、圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.
1.什么是圆周角?
●O
B
A
C
D
E
温故知新:
圆周角定理
圆周角定理 一条弧所对的圆周角等于它所对的圆心角的一半.
老师提示:圆周角定理是承上启下的知识点,要予以重视.
●O
A
B
C
●O
A
B
C
●O
A
B
C
即 ∠ABC = ∠AOC.
温故知新:
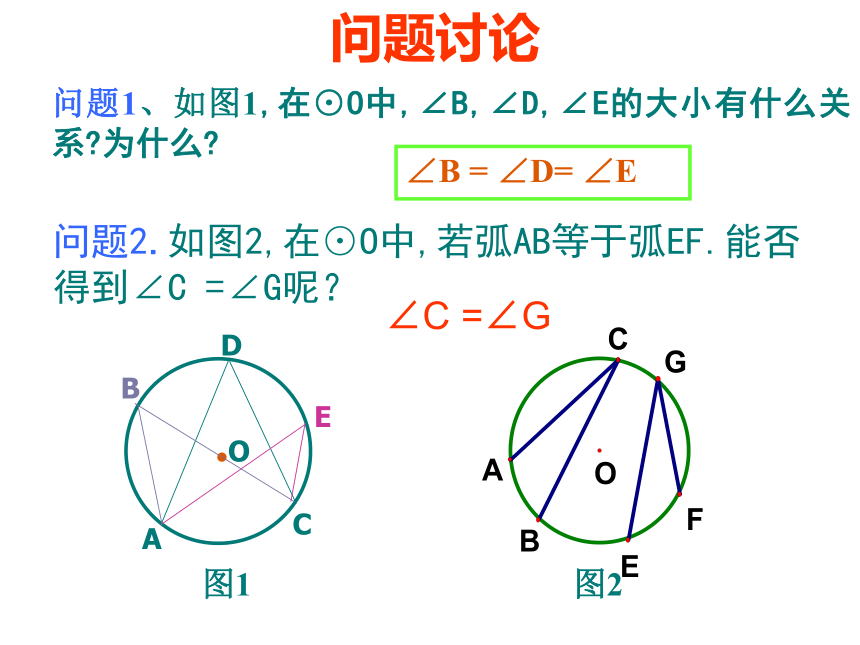
问题2.如图2,在⊙O中,若弧AB等于弧EF.能否得到∠C =∠G呢?
图2
问题1、如图1,在⊙O中,∠B,∠D,∠E的大小有什么关系 为什么
∠B = ∠D= ∠E
●O
B
A
C
D
E
图1
∠C =∠G
问题讨论
问题讨论
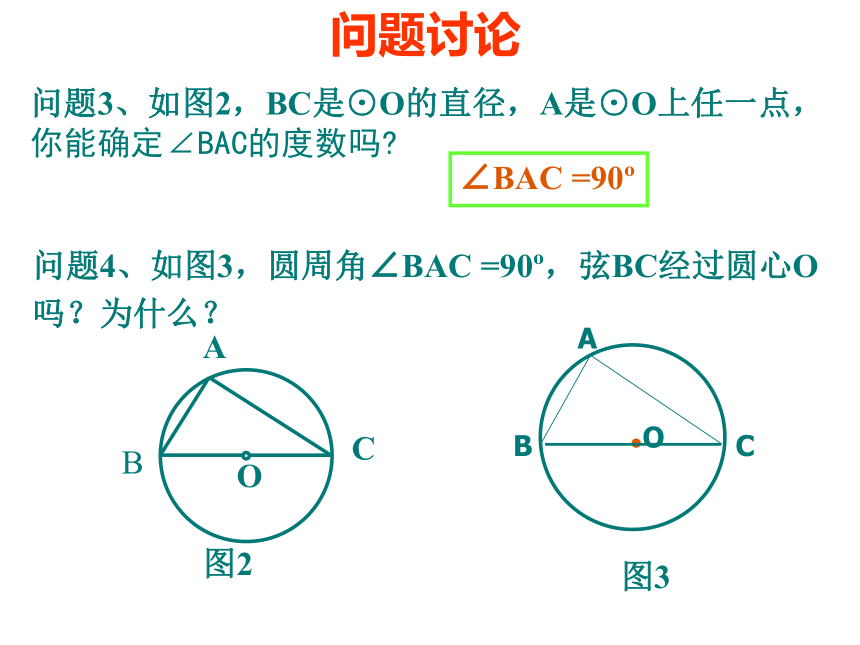
问题3、如图2,BC是⊙O的直径,A是⊙O上任一点,你能确定∠BAC的度数吗
B
A
O
C
图2
问题4、如图3,圆周角∠BAC =90 ,弦BC经过圆心O吗?为什么?
∠BAC =90
●O
B
C
A
图3
问题解答
1、圆周角定理的推论1:
同圆或等圆中,同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等。
2、圆周角定理的推论2:
半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径。
用于找相等的角
用于找相等的弧
用于判断某个圆周角是否是直角
用于判断某条线是否过圆心
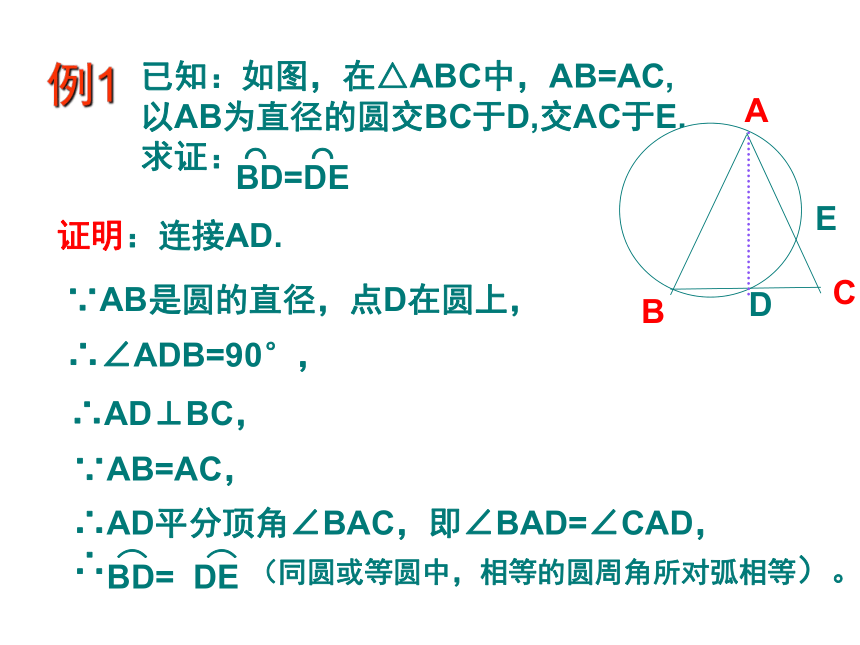
例1
已知:如图,在△ABC中,AB=AC,
以AB为直径的圆交BC于D,交AC于E,
求证:⌒ ⌒
BD=DE
证明:连接AD.
∵AB是圆的直径,点D在圆上,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴AD平分顶角∠BAC,即∠BAD=∠CAD,
∴ ⌒ ⌒
BD= DE
(同圆或等圆中,相等的圆周角所对弧相等)。
A
B
C
D
E
例2
如图,P是△ABC的外接圆上的一点
∠APC=∠CPB=60°。求证:△ABC是等边三角形
·
·
A
P
B
C
O
证明:∵∠ABC和∠APC
都是⌒所对的圆周角。
AC
∴∠ABC=∠APC=60°
(同弧所对的圆周角相等)
同理,∵∠BAC和∠CPB都是⌒ 所对的圆周角,
BC
∴∠BAC=∠CPB=60°。
∴△ABC等边三角形。
·o
C
E
A
B
P
(1)当船与两个灯塔的夹角∠α大于
“危险角”时,船位于哪个区域 为什么
(2)当船与两个灯塔的夹角∠α小
于“危险角”时,船位于哪个区域
为什么
船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁.如图所示,A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,C表示一个危险临界点∠ACB就是“危险角”,当船与两个灯塔的夹角大于“危险角”时,就有可能触礁.
做一做
·o
C
E
A
B
P
答(1)船位于暗礁区域内(即圆o内).
理由:假设船在⊙O上,则有∠α=∠C,这与
∠α> ∠ C矛盾.所以船不可能在⊙O上;
假设船在⊙O外,则有∠ α< ∠AEB,即
∠ α < ∠C,这与∠ α > ∠C矛盾.
所以:
船不可能在⊙O外.
因此,船只能位于⊙O内.
(2)船位于暗礁区域外(即⊙O外).
2、如图,哪个角与∠BAC 相等
1、为什么有些电影院的坐位排列(横排)呈圆弧形 说一说这种设计的合理性
随堂练习
3.如图.⊙O的直径AB=10cm,C是⊙O上的一点.
∠ABC =30°.求AC的长.
解:
∵ AB是直径
∴ ∠ACB= 90
即:AC = 5cm
∵∠ABC= 30°
∴AC= AB
随堂练习
4.小明想用直角尺检查某些工件是否恰好为半圆形. 根据下图, 你能判断哪个是半圆形吗 为什么
随堂练习
我手中有一个量角器和一个直角三角尺,你用什么方法可以确定量角器是半圆形
想一想
讨论与思考
A
B
C
D
O
E
如图,CD是⊙O的直径,弦AB⊥CD于E,那么你能得到什么结论?
结论:
(1)AE = BE,AC = BC,AD = BD
(2)AC = BC,∠CAB = ∠ABC = ∠D,
∠ACE =∠BCE =∠DAB
(3)BC2 = AC2 = CE · CD,AD2 = DE · DC
BE2 = AE2 = DE · CE
1、本节课我们学习了哪些知识?
2、圆周角定理及其推论的用途你都知道 了吗?
3、证明题思路的寻找方法如何?
4、证明等积式的一般思路你掌握了吗?
●O
B
A
C
D
E
特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
1、圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.
1.什么是圆周角?
●O
B
A
C
D
E
温故知新:
圆周角定理
圆周角定理 一条弧所对的圆周角等于它所对的圆心角的一半.
老师提示:圆周角定理是承上启下的知识点,要予以重视.
●O
A
B
C
●O
A
B
C
●O
A
B
C
即 ∠ABC = ∠AOC.
温故知新:
问题2.如图2,在⊙O中,若弧AB等于弧EF.能否得到∠C =∠G呢?
图2
问题1、如图1,在⊙O中,∠B,∠D,∠E的大小有什么关系 为什么
∠B = ∠D= ∠E
●O
B
A
C
D
E
图1
∠C =∠G
问题讨论
问题讨论
问题3、如图2,BC是⊙O的直径,A是⊙O上任一点,你能确定∠BAC的度数吗
B
A
O
C
图2
问题4、如图3,圆周角∠BAC =90 ,弦BC经过圆心O吗?为什么?
∠BAC =90
●O
B
C
A
图3
问题解答
1、圆周角定理的推论1:
同圆或等圆中,同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等。
2、圆周角定理的推论2:
半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径。
用于找相等的角
用于找相等的弧
用于判断某个圆周角是否是直角
用于判断某条线是否过圆心
例1
已知:如图,在△ABC中,AB=AC,
以AB为直径的圆交BC于D,交AC于E,
求证:⌒ ⌒
BD=DE
证明:连接AD.
∵AB是圆的直径,点D在圆上,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴AD平分顶角∠BAC,即∠BAD=∠CAD,
∴ ⌒ ⌒
BD= DE
(同圆或等圆中,相等的圆周角所对弧相等)。
A
B
C
D
E
例2
如图,P是△ABC的外接圆上的一点
∠APC=∠CPB=60°。求证:△ABC是等边三角形
·
·
A
P
B
C
O
证明:∵∠ABC和∠APC
都是⌒所对的圆周角。
AC
∴∠ABC=∠APC=60°
(同弧所对的圆周角相等)
同理,∵∠BAC和∠CPB都是⌒ 所对的圆周角,
BC
∴∠BAC=∠CPB=60°。
∴△ABC等边三角形。
·o
C
E
A
B
P
(1)当船与两个灯塔的夹角∠α大于
“危险角”时,船位于哪个区域 为什么
(2)当船与两个灯塔的夹角∠α小
于“危险角”时,船位于哪个区域
为什么
船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁.如图所示,A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,C表示一个危险临界点∠ACB就是“危险角”,当船与两个灯塔的夹角大于“危险角”时,就有可能触礁.
做一做
·o
C
E
A
B
P
答(1)船位于暗礁区域内(即圆o内).
理由:假设船在⊙O上,则有∠α=∠C,这与
∠α> ∠ C矛盾.所以船不可能在⊙O上;
假设船在⊙O外,则有∠ α< ∠AEB,即
∠ α < ∠C,这与∠ α > ∠C矛盾.
所以:
船不可能在⊙O外.
因此,船只能位于⊙O内.
(2)船位于暗礁区域外(即⊙O外).
2、如图,哪个角与∠BAC 相等
1、为什么有些电影院的坐位排列(横排)呈圆弧形 说一说这种设计的合理性
随堂练习
3.如图.⊙O的直径AB=10cm,C是⊙O上的一点.
∠ABC =30°.求AC的长.
解:
∵ AB是直径
∴ ∠ACB= 90
即:AC = 5cm
∵∠ABC= 30°
∴AC= AB
随堂练习
4.小明想用直角尺检查某些工件是否恰好为半圆形. 根据下图, 你能判断哪个是半圆形吗 为什么
随堂练习
我手中有一个量角器和一个直角三角尺,你用什么方法可以确定量角器是半圆形
想一想
讨论与思考
A
B
C
D
O
E
如图,CD是⊙O的直径,弦AB⊥CD于E,那么你能得到什么结论?
结论:
(1)AE = BE,AC = BC,AD = BD
(2)AC = BC,∠CAB = ∠ABC = ∠D,
∠ACE =∠BCE =∠DAB
(3)BC2 = AC2 = CE · CD,AD2 = DE · DC
BE2 = AE2 = DE · CE
1、本节课我们学习了哪些知识?
2、圆周角定理及其推论的用途你都知道 了吗?
3、证明题思路的寻找方法如何?
4、证明等积式的一般思路你掌握了吗?
