2021-2022学年度沪科版九年级数学下册课件 24.7 弧长与扇形的面积(第2课时)(共18张PPT)
文档属性
| 名称 | 2021-2022学年度沪科版九年级数学下册课件 24.7 弧长与扇形的面积(第2课时)(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 11:24:01 | ||
图片预览





文档简介
(共18张PPT)
24.7 弧长与扇形的面积 (第2课时)
请 你 欣 赏
根据你以前的所学,说说你对圆锥的一些认识。
圆锥的高
母线
S
A
O
B
r
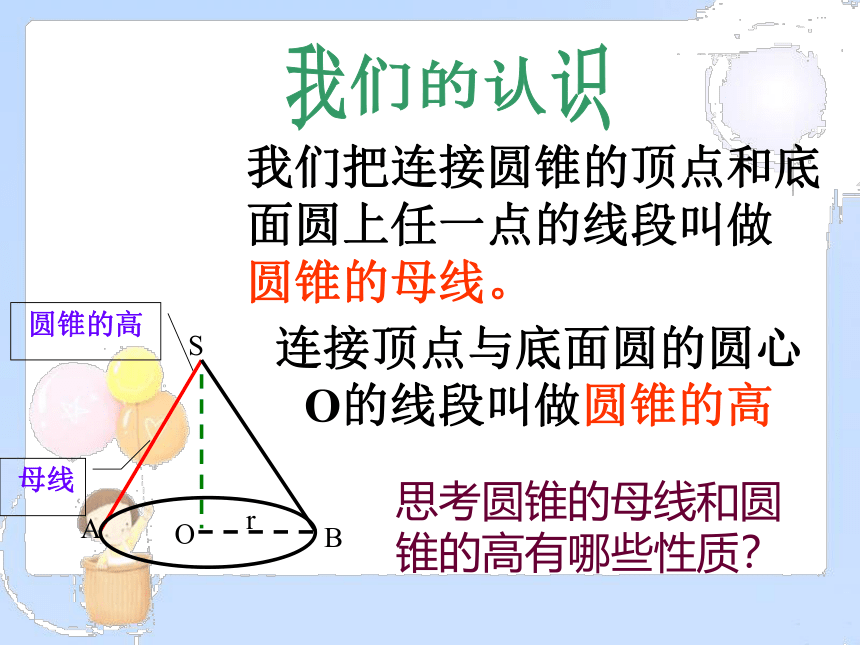
我们把连接圆锥的顶点和底面圆上任一点的线段叫做
圆锥的母线。
连接顶点与底面圆的圆心O的线段叫做圆锥的高
思考圆锥的母线和圆锥的高有哪些性质?
h
l
r
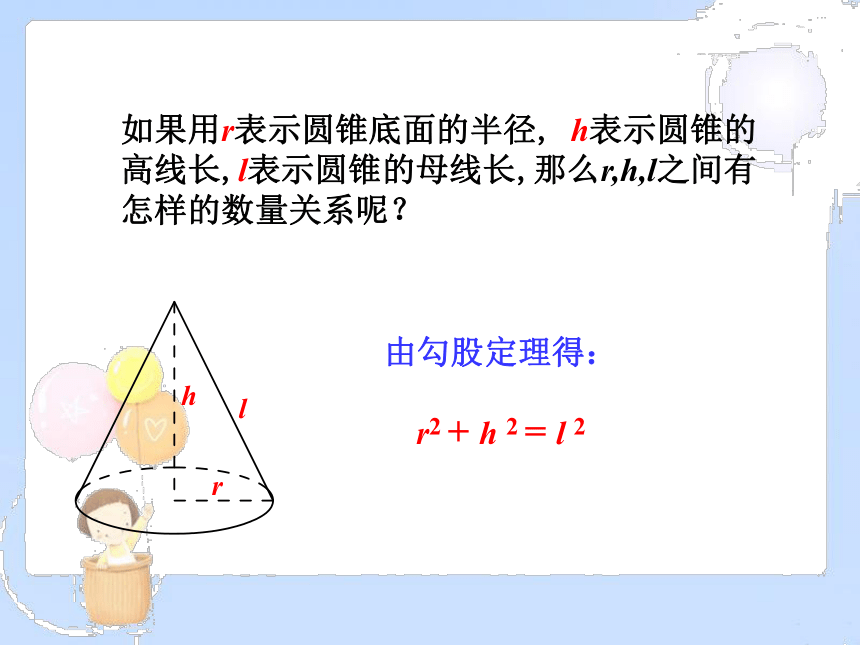
由勾股定理得:
如果用r表示圆锥底面的半径, h表示圆锥的高线长,l表示圆锥的母线长,那么r,h,l之间有怎样的数量关系呢?
r2 + h 2 = l 2
填空: 根据下列条件求值(其中r、h、l分别是圆锥的底面半径、高线、母线长)
(1) l = 2,r = 1 则 h =_______
(2) h = 3, r = 4 则 l =_______
(3) l = 10, h = 8 则r =_______
5
6
A
B
O
C
圆锥的侧面展开图是扇形
A
B
O
C
其侧面展开图扇形的半径=母线的长l
l
S
A
O
B
r
S
A
O
B
侧面展开图扇形的弧长=底面周长
请推导出圆锥的侧面积公式.
S 侧 =πrl (r表示圆锥底面的半径, l 表示圆锥的母线长 )
圆锥的侧面积与底面积的和叫做圆锥的全面积(或表面积).
l
r
做一做
(2)已知一个圆锥的底面半径为12cm,母线长为20cm,则这个圆锥的侧面积为_________,全面积为_______
(1)已知一个圆锥的高为6cm,半径为8cm,则这个圆锥的母长为_______
例1、圆锥形烟囱帽(如图)的母线长为80cm,高为38.7cm,求这个烟囱帽的面积( 取3.14,结果保留2个有效数字)
解:∵l=80,h=38.7
∴r=
∴S侧=πrl≈3.14×70×80≈1.8×104(cm2)
答:烟囱帽的面积约为1.8×104cm2。
l
h
r
例2:如图所示的扇形中,半径R=10,圆心角θ=144°用这个扇形围成一个圆锥的侧面.
(1)求这个圆锥的底面半径r;
(2)求这个圆锥的高.
A
C
O
B
r
r=4
1.圆锥的底面直径为80cm.母线长为90cm,求它的全面积.
S全=5200 cm2
2.扇形的半径为30,圆心角为120°用它做一个圆锥模型的侧面,求这个圆锥的底面半径和高.
r=10;h=
做一做
例3、蒙古包可以近似地看成由圆锥和圆柱组成的.如果想在某个牧区搭建20个底面积为35m2,高为3.5m,外围高1.5m的蒙古包.那么至少需要用多少m2的帆布 (结果取整数).
·
·
r
h1
h2
思考题:如图,圆锥的底面半径为1,母线长为3,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬到过母线AB的轴截面上另一母线AC上,问它爬行的最短路线是多少?
A
B
C
24.7 弧长与扇形的面积 (第2课时)
请 你 欣 赏
根据你以前的所学,说说你对圆锥的一些认识。
圆锥的高
母线
S
A
O
B
r
我们把连接圆锥的顶点和底面圆上任一点的线段叫做
圆锥的母线。
连接顶点与底面圆的圆心O的线段叫做圆锥的高
思考圆锥的母线和圆锥的高有哪些性质?
h
l
r
由勾股定理得:
如果用r表示圆锥底面的半径, h表示圆锥的高线长,l表示圆锥的母线长,那么r,h,l之间有怎样的数量关系呢?
r2 + h 2 = l 2
填空: 根据下列条件求值(其中r、h、l分别是圆锥的底面半径、高线、母线长)
(1) l = 2,r = 1 则 h =_______
(2) h = 3, r = 4 则 l =_______
(3) l = 10, h = 8 则r =_______
5
6
A
B
O
C
圆锥的侧面展开图是扇形
A
B
O
C
其侧面展开图扇形的半径=母线的长l
l
S
A
O
B
r
S
A
O
B
侧面展开图扇形的弧长=底面周长
请推导出圆锥的侧面积公式.
S 侧 =πrl (r表示圆锥底面的半径, l 表示圆锥的母线长 )
圆锥的侧面积与底面积的和叫做圆锥的全面积(或表面积).
l
r
做一做
(2)已知一个圆锥的底面半径为12cm,母线长为20cm,则这个圆锥的侧面积为_________,全面积为_______
(1)已知一个圆锥的高为6cm,半径为8cm,则这个圆锥的母长为_______
例1、圆锥形烟囱帽(如图)的母线长为80cm,高为38.7cm,求这个烟囱帽的面积( 取3.14,结果保留2个有效数字)
解:∵l=80,h=38.7
∴r=
∴S侧=πrl≈3.14×70×80≈1.8×104(cm2)
答:烟囱帽的面积约为1.8×104cm2。
l
h
r
例2:如图所示的扇形中,半径R=10,圆心角θ=144°用这个扇形围成一个圆锥的侧面.
(1)求这个圆锥的底面半径r;
(2)求这个圆锥的高.
A
C
O
B
r
r=4
1.圆锥的底面直径为80cm.母线长为90cm,求它的全面积.
S全=5200 cm2
2.扇形的半径为30,圆心角为120°用它做一个圆锥模型的侧面,求这个圆锥的底面半径和高.
r=10;h=
做一做
例3、蒙古包可以近似地看成由圆锥和圆柱组成的.如果想在某个牧区搭建20个底面积为35m2,高为3.5m,外围高1.5m的蒙古包.那么至少需要用多少m2的帆布 (结果取整数).
·
·
r
h1
h2
思考题:如图,圆锥的底面半径为1,母线长为3,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬到过母线AB的轴截面上另一母线AC上,问它爬行的最短路线是多少?
A
B
C
