2021-2022学年度沪科版九年级数学下册课件 24.4.直线与圆的位置关系(3)(共14张PPT)
文档属性
| 名称 | 2021-2022学年度沪科版九年级数学下册课件 24.4.直线与圆的位置关系(3)(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 551.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
学 习 目 的
掌握切线的性质定理及其推论,并能运用它们解决有关问题.
问题:
⒈前面我们已学过的切线的性质有哪些?
答:
①切线和圆有且只有一个公共点;
②切线和圆心的距离等于半径.
⒉切线还有什么性质?
观察右图:
如果直线AT是⊙O的切线,A为切点,那么AT和半径OA是不是一定垂直?
A
T
O
M
直线AT切圆O于A AT OA
B
C
[切线的性质定理]
圆的切线垂直于经过切点的半径
推论1 经过圆心且垂直于切线的直线必经过切点
推论2 经过切点且垂直于切线的直线必经过圆心
经过圆心
垂直于切线
直线经过切点
垂直于切线
经过圆心
直线经过切点
直线经过切点
经过圆心
切线垂直于半径
1
2
3
O
B
A
C
D
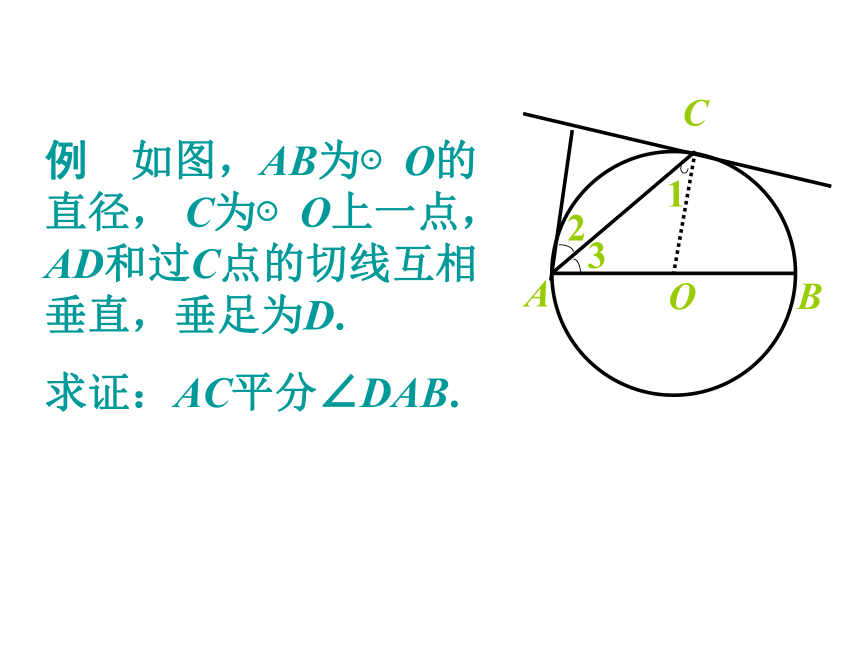
例 如图,AB为⊙O的直径, C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.
求证:AC平分∠DAB.
CD是⊙O的切线
OC⊥CD
AD⊥CD
OC∥AD
∠1=∠2
OC = OA
∠1=∠3
∠1=∠3
AC平分∠DAB
1
2
3
O
B
A
C
D
证明:如图,连接OC.
(2) 如果半径OA⊥AB,那么AB是
按图填空:(口答)
(1) 如果AB切⊙O于A,
那么
A
O
B
⊙O的切线
切点
(3) 如果AB是⊙O的切线,OA⊥AB,那么A是
⊥
OA
AB.
练习2
如图的两个圆是以O为圆心的同心圆,大圆的弦AB是小圆的切线, C为切点.求证:C是AB的中点.
C
A
B
O
证明:如图,
∴ C是AB的中点.
AC=BC
根据垂径定理,得
OC⊥AB
连接OC, 则
D
C
B
O
A
练习3
如图,在⊙O中,AB为直径, AD为弦, 过B点的切线与AD的延长线交于点C,且AD=DC
求∠ABD的度数.
解: AB为直径
BC为切线
∠ABC=90°
△ABC为直角三角形
AD=DC
∠ADB=90°
AD=DB
∠ADC=90°
△ABD为等腰直角三角形
∠ABD=45°
求证:经过直径两端点的切线互相平行
练习4
D
C
B
A
O
已知:如图,AB 是⊙O的直径,AC、BD是⊙O的切线.
证明:如图,
AB 是⊙O的直径
AC、BD是⊙O的切线
AB⊥AC
AB⊥BD
AC∥BD
求证: AC∥BD
① 切线和圆有且只有一个公共点
③ 圆的切线垂直于经过切点的半径
④ 经过圆心且垂直于切线的直线必经过切点
⑤ 经过切点且垂直于切线的直线必经过圆心
② 切线和圆心的距离等于半径
再见
学 习 目 的
掌握切线的性质定理及其推论,并能运用它们解决有关问题.
问题:
⒈前面我们已学过的切线的性质有哪些?
答:
①切线和圆有且只有一个公共点;
②切线和圆心的距离等于半径.
⒉切线还有什么性质?
观察右图:
如果直线AT是⊙O的切线,A为切点,那么AT和半径OA是不是一定垂直?
A
T
O
M
直线AT切圆O于A AT OA
B
C
[切线的性质定理]
圆的切线垂直于经过切点的半径
推论1 经过圆心且垂直于切线的直线必经过切点
推论2 经过切点且垂直于切线的直线必经过圆心
经过圆心
垂直于切线
直线经过切点
垂直于切线
经过圆心
直线经过切点
直线经过切点
经过圆心
切线垂直于半径
1
2
3
O
B
A
C
D
例 如图,AB为⊙O的直径, C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.
求证:AC平分∠DAB.
CD是⊙O的切线
OC⊥CD
AD⊥CD
OC∥AD
∠1=∠2
OC = OA
∠1=∠3
∠1=∠3
AC平分∠DAB
1
2
3
O
B
A
C
D
证明:如图,连接OC.
(2) 如果半径OA⊥AB,那么AB是
按图填空:(口答)
(1) 如果AB切⊙O于A,
那么
A
O
B
⊙O的切线
切点
(3) 如果AB是⊙O的切线,OA⊥AB,那么A是
⊥
OA
AB.
练习2
如图的两个圆是以O为圆心的同心圆,大圆的弦AB是小圆的切线, C为切点.求证:C是AB的中点.
C
A
B
O
证明:如图,
∴ C是AB的中点.
AC=BC
根据垂径定理,得
OC⊥AB
连接OC, 则
D
C
B
O
A
练习3
如图,在⊙O中,AB为直径, AD为弦, 过B点的切线与AD的延长线交于点C,且AD=DC
求∠ABD的度数.
解: AB为直径
BC为切线
∠ABC=90°
△ABC为直角三角形
AD=DC
∠ADB=90°
AD=DB
∠ADC=90°
△ABD为等腰直角三角形
∠ABD=45°
求证:经过直径两端点的切线互相平行
练习4
D
C
B
A
O
已知:如图,AB 是⊙O的直径,AC、BD是⊙O的切线.
证明:如图,
AB 是⊙O的直径
AC、BD是⊙O的切线
AB⊥AC
AB⊥BD
AC∥BD
求证: AC∥BD
① 切线和圆有且只有一个公共点
③ 圆的切线垂直于经过切点的半径
④ 经过圆心且垂直于切线的直线必经过切点
⑤ 经过切点且垂直于切线的直线必经过圆心
② 切线和圆心的距离等于半径
再见
