2021-2022学年度沪科版九年级数学下册 26.2 .3等可能情形下的概率计算课件(共12张PPT)
文档属性
| 名称 | 2021-2022学年度沪科版九年级数学下册 26.2 .3等可能情形下的概率计算课件(共12张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 676.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 13:59:17 | ||
图片预览

文档简介
(共12张PPT)
26.2 等可能情形下的概率计算
(第3课时)
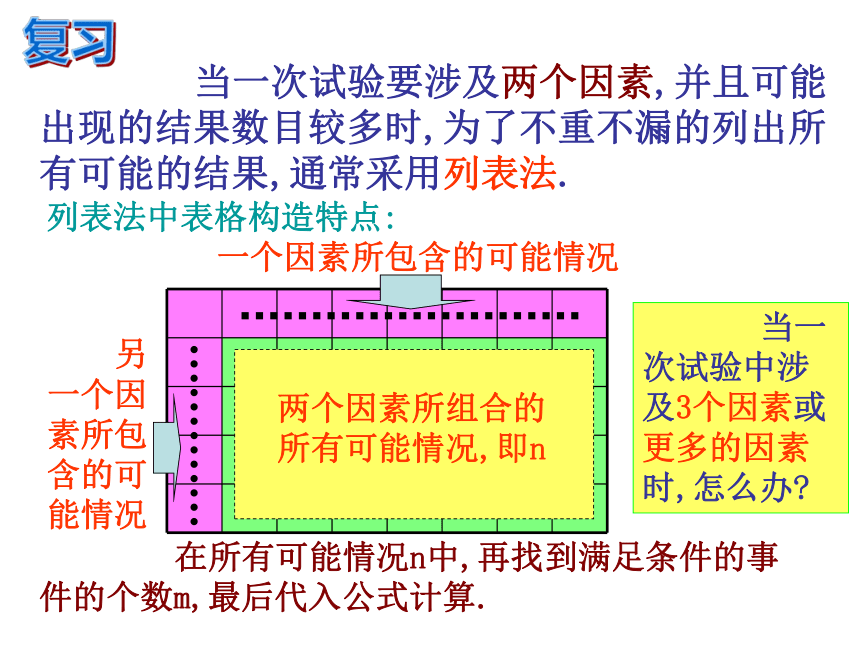
当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表法.
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即n
在所有可能情况n中,再找到满足条件的事件的个数m,最后代入公式计算.
列表法中表格构造特点:
当一次试验中涉及3个因素或更多的因素时,怎么办
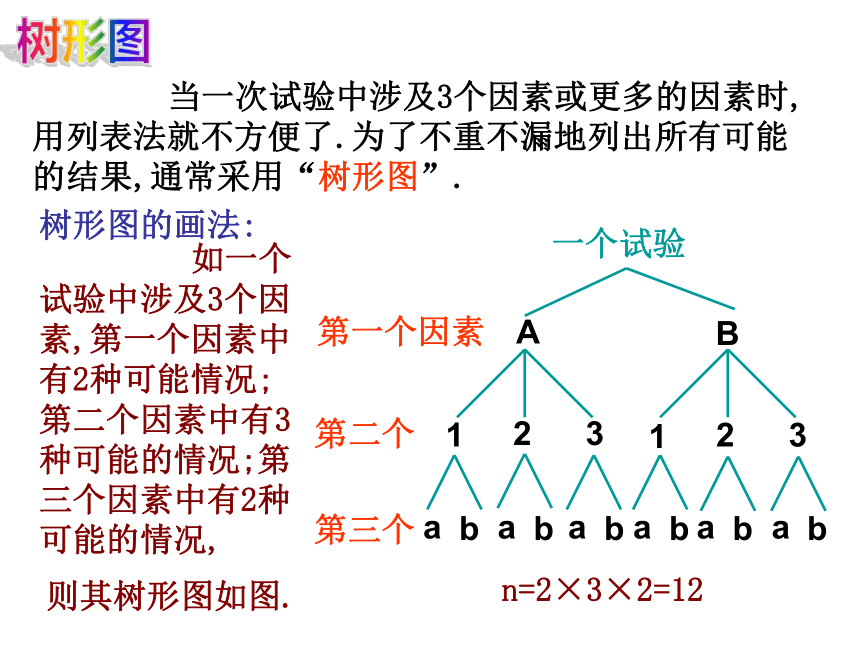
当一次试验中涉及3个因素或更多的因素时,用列表法就不方便了.为了不重不漏地列出所有可能的结果,通常采用“树形图”.
树形图的画法:
一个试验
第一个因素
第二个
第三个
如一个试验中涉及3个因素,第一个因素中有2种可能情况;第二个因素中有3种可能的情况;第三个因素中有2种可能的情况,
A
B
1
2
3
1
2
3
a
b
a
b
a
b
a
b
a
b
a
b
则其树形图如图.
n=2×3×2=12
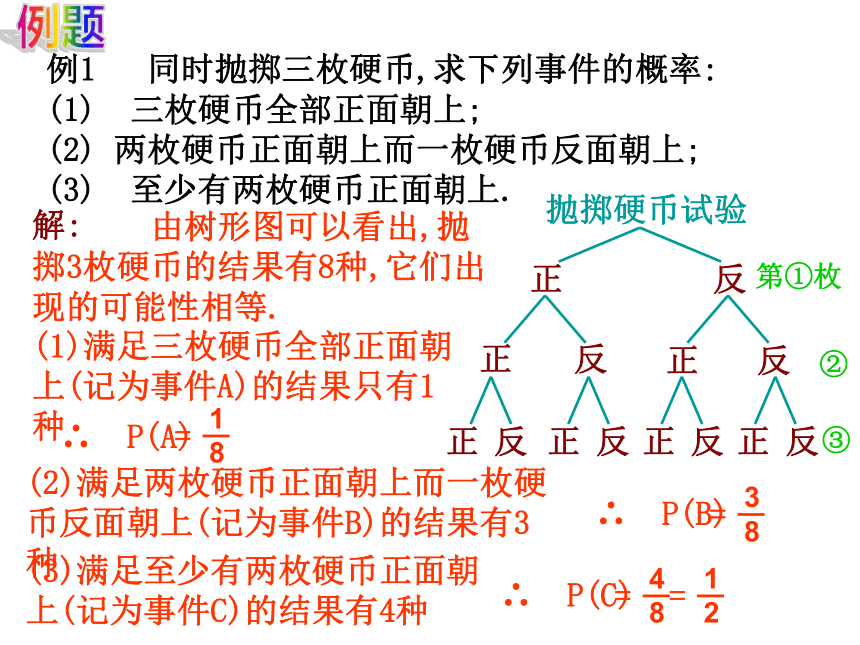
例1 同时抛掷三枚硬币,求下列事件的概率:
(1) 三枚硬币全部正面朝上;
(2) 两枚硬币正面朝上而一枚硬币反面朝上;
(3) 至少有两枚硬币正面朝上.
正
反
正
反
正
反
正
反
正
反
正
反
正
反
抛掷硬币试验
解:
由树形图可以看出,抛掷3枚硬币的结果有8种,它们出现的可能性相等.
∴ P(A)
(1)满足三枚硬币全部正面朝上(记为事件A)的结果只有1种
1
8
=
∴ P(B)
3
8
=
(2)满足两枚硬币正面朝上而一枚硬币反面朝上(记为事件B)的结果有3种
(3)满足至少有两枚硬币正面朝上(记为事件C)的结果有4种
∴ P(C)
4
8
=
1
2
=
第①枚
②
③
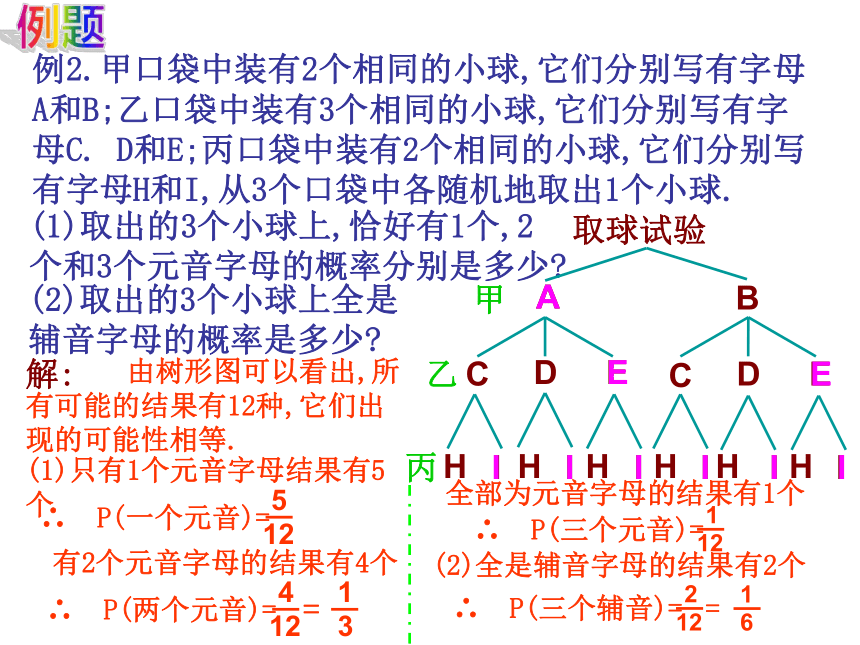
例2.甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C. D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I,从3个口袋中各随机地取出1个小球.
(2)取出的3个小球上全是辅音字母的概率是多少
(1)取出的3个小球上,恰好有1个,2个和3个元音字母的概率分别是多少
取球试验
甲
乙
丙
A
B
C
D
E
C
D
E
H
I
H
I
H
I
H
I
H
I
H
I
解:
由树形图可以看出,所有可能的结果有12种,它们出现的可能性相等.
∴ P(一个元音)=
(1)只有1个元音字母结果有5个
5
12
∴ P(两个元音)=
有2个元音字母的结果有4个
4
12
1
3
=
∴ P(三个元音)=
全部为元音字母的结果有1个
1
12
∴ P(三个辅音)=
(2)全是辅音字母的结果有2个
1
6
=
2
12
A
E
E
I
I
I
I
I
I
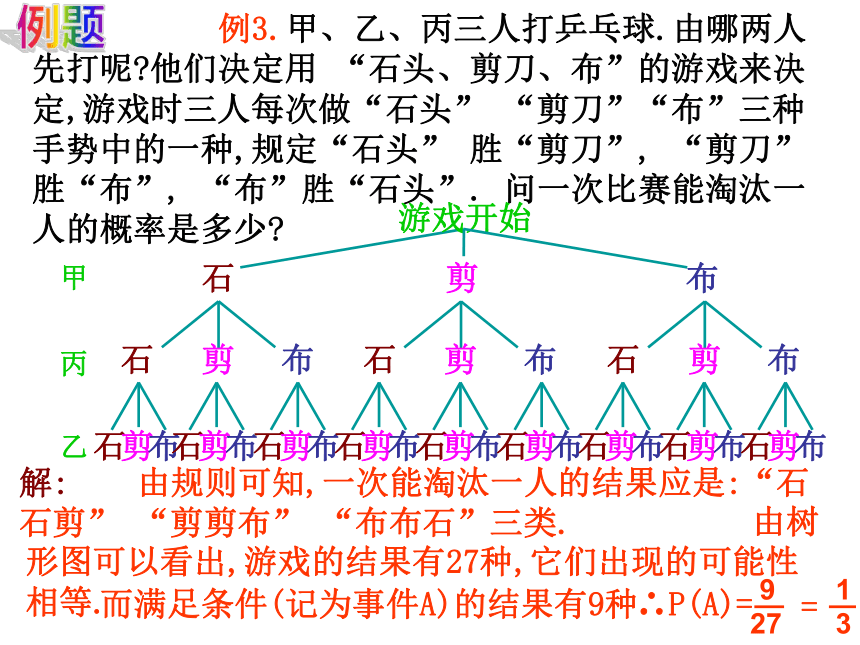
例3.甲、乙、丙三人打乒乓球.由哪两人先打呢 他们决定用 “石头、剪刀、布”的游戏来决定,游戏时三人每次做“石头” “剪刀”“布”三种手势中的一种,规定“石头” 胜“剪刀”, “剪刀”胜“布”, “布”胜“石头”. 问一次比赛能淘汰一人的概率是多少
石
剪
布
石
游戏开始
甲
乙
丙
石
石
剪
布
石
剪
布
石
剪
布
石
剪
布
石
剪
布
石
剪
布
石
剪
布
石
剪
布
剪
布
石
剪
布
石
剪
布
剪
布
解:
由树形图可以看出,游戏的结果有27种,它们出现的可能性相等.
由规则可知,一次能淘汰一人的结果应是:“石石剪” “剪剪布” “布布石”三类.
而满足条件(记为事件A)的结果有9种
∴P(A)=
1
3
=
9
27
(1) 列表法和树形图法的优点是什么
(2)什么时候使用“列表法”方便 什么时候使用“树形图法”方便
(1)优点:利用树形图或表格可以清晰地表示出某个事件发生的所有可能出现的结果;从而较方便地求出某些事件发生的概率.
(2)当试验包含两步时,列表法比较方便,当然,此时也可以用树形图法;
当试验在三步或三步以上时,用树形图法方便.
1.经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种可能性大小相同,当有三辆汽车经过这个十字路口时,求下列事件的概率:
(1)三辆车全部继续直行;
(2)两辆车向右转,一辆车向左转;
(3)至少有两辆车向左转.
所以
1
9
(1)
(2)
(3)
1
27
7
27
2.用数字1、2、3,组成三位数,求其中恰有2个相同的数字的概率.
1
2
3
1
组数开始
百位
个位
十位
1
2
3
1
2
3
1
2
3
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
解:
由树形图可以看出,所有可能的结果有27种,它们出现的可能性相等.
其中恰有2个数字相同的结果有18个.
∴ P(恰有两个数字相同)=
18
27
2
3
=
4.把3个不同的球任意投入3个不同的盒子内(每盒装球不限),计算: (1)无空盒的概率; (2)恰有一个空盒的概率.
1
2
3
盒1
投球开始
球①
球③
球②
1
2
3
1
2
3
1
2
3
盒2
盒3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
解:
由树形图可以看出,所有可能的结果有27种,它们出现的可能性相等.
∴ P(无空盒)=
(1)无空盒的结果有6个
6
27
2
9
=
(2)恰有一个空盒的结果有18个
∴ P(恰有一个空盒)=
18
27
2
3
=
26.2 等可能情形下的概率计算
(第3课时)
当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表法.
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即n
在所有可能情况n中,再找到满足条件的事件的个数m,最后代入公式计算.
列表法中表格构造特点:
当一次试验中涉及3个因素或更多的因素时,怎么办
当一次试验中涉及3个因素或更多的因素时,用列表法就不方便了.为了不重不漏地列出所有可能的结果,通常采用“树形图”.
树形图的画法:
一个试验
第一个因素
第二个
第三个
如一个试验中涉及3个因素,第一个因素中有2种可能情况;第二个因素中有3种可能的情况;第三个因素中有2种可能的情况,
A
B
1
2
3
1
2
3
a
b
a
b
a
b
a
b
a
b
a
b
则其树形图如图.
n=2×3×2=12
例1 同时抛掷三枚硬币,求下列事件的概率:
(1) 三枚硬币全部正面朝上;
(2) 两枚硬币正面朝上而一枚硬币反面朝上;
(3) 至少有两枚硬币正面朝上.
正
反
正
反
正
反
正
反
正
反
正
反
正
反
抛掷硬币试验
解:
由树形图可以看出,抛掷3枚硬币的结果有8种,它们出现的可能性相等.
∴ P(A)
(1)满足三枚硬币全部正面朝上(记为事件A)的结果只有1种
1
8
=
∴ P(B)
3
8
=
(2)满足两枚硬币正面朝上而一枚硬币反面朝上(记为事件B)的结果有3种
(3)满足至少有两枚硬币正面朝上(记为事件C)的结果有4种
∴ P(C)
4
8
=
1
2
=
第①枚
②
③
例2.甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C. D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I,从3个口袋中各随机地取出1个小球.
(2)取出的3个小球上全是辅音字母的概率是多少
(1)取出的3个小球上,恰好有1个,2个和3个元音字母的概率分别是多少
取球试验
甲
乙
丙
A
B
C
D
E
C
D
E
H
I
H
I
H
I
H
I
H
I
H
I
解:
由树形图可以看出,所有可能的结果有12种,它们出现的可能性相等.
∴ P(一个元音)=
(1)只有1个元音字母结果有5个
5
12
∴ P(两个元音)=
有2个元音字母的结果有4个
4
12
1
3
=
∴ P(三个元音)=
全部为元音字母的结果有1个
1
12
∴ P(三个辅音)=
(2)全是辅音字母的结果有2个
1
6
=
2
12
A
E
E
I
I
I
I
I
I
例3.甲、乙、丙三人打乒乓球.由哪两人先打呢 他们决定用 “石头、剪刀、布”的游戏来决定,游戏时三人每次做“石头” “剪刀”“布”三种手势中的一种,规定“石头” 胜“剪刀”, “剪刀”胜“布”, “布”胜“石头”. 问一次比赛能淘汰一人的概率是多少
石
剪
布
石
游戏开始
甲
乙
丙
石
石
剪
布
石
剪
布
石
剪
布
石
剪
布
石
剪
布
石
剪
布
石
剪
布
石
剪
布
剪
布
石
剪
布
石
剪
布
剪
布
解:
由树形图可以看出,游戏的结果有27种,它们出现的可能性相等.
由规则可知,一次能淘汰一人的结果应是:“石石剪” “剪剪布” “布布石”三类.
而满足条件(记为事件A)的结果有9种
∴P(A)=
1
3
=
9
27
(1) 列表法和树形图法的优点是什么
(2)什么时候使用“列表法”方便 什么时候使用“树形图法”方便
(1)优点:利用树形图或表格可以清晰地表示出某个事件发生的所有可能出现的结果;从而较方便地求出某些事件发生的概率.
(2)当试验包含两步时,列表法比较方便,当然,此时也可以用树形图法;
当试验在三步或三步以上时,用树形图法方便.
1.经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种可能性大小相同,当有三辆汽车经过这个十字路口时,求下列事件的概率:
(1)三辆车全部继续直行;
(2)两辆车向右转,一辆车向左转;
(3)至少有两辆车向左转.
所以
1
9
(1)
(2)
(3)
1
27
7
27
2.用数字1、2、3,组成三位数,求其中恰有2个相同的数字的概率.
1
2
3
1
组数开始
百位
个位
十位
1
2
3
1
2
3
1
2
3
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
解:
由树形图可以看出,所有可能的结果有27种,它们出现的可能性相等.
其中恰有2个数字相同的结果有18个.
∴ P(恰有两个数字相同)=
18
27
2
3
=
4.把3个不同的球任意投入3个不同的盒子内(每盒装球不限),计算: (1)无空盒的概率; (2)恰有一个空盒的概率.
1
2
3
盒1
投球开始
球①
球③
球②
1
2
3
1
2
3
1
2
3
盒2
盒3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
解:
由树形图可以看出,所有可能的结果有27种,它们出现的可能性相等.
∴ P(无空盒)=
(1)无空盒的结果有6个
6
27
2
9
=
(2)恰有一个空盒的结果有18个
∴ P(恰有一个空盒)=
18
27
2
3
=
