湘教版七上数学4.2线段、射线、直线(2)课件(共30张PPT)
文档属性
| 名称 | 湘教版七上数学4.2线段、射线、直线(2)课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 30.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 00:00:00 | ||
图片预览










文档简介
(共30张PPT)
4.2 线段、射线、直线(2)
湘教版 七年级上
教学目标
1. 理解线段大小的比较方法,知道线段比较的结果;
2. 学会线段长度,大小关系,线段和、差的表示方法;
3. 理解线段最短的基本事实及两点之间的距离的概念;
4. 学会用尺规作图方法作线段,理解线段的中点概念;
5. 进一步学会阅读几何语言,提高作图能力。
新知导入
如图,线段AB、BC、CA分别三角形中的三条边,你能解决下面问题吗?
(1)线段AB、BC、CA中,哪一条线段最长?
(2)AB、CA的长度和与线段BC的长度如何比较?
A
B
C
要解决上述问题,我们要学会用圆规等工具作图的方法,并学会线段的大小比较方法。
新知讲解
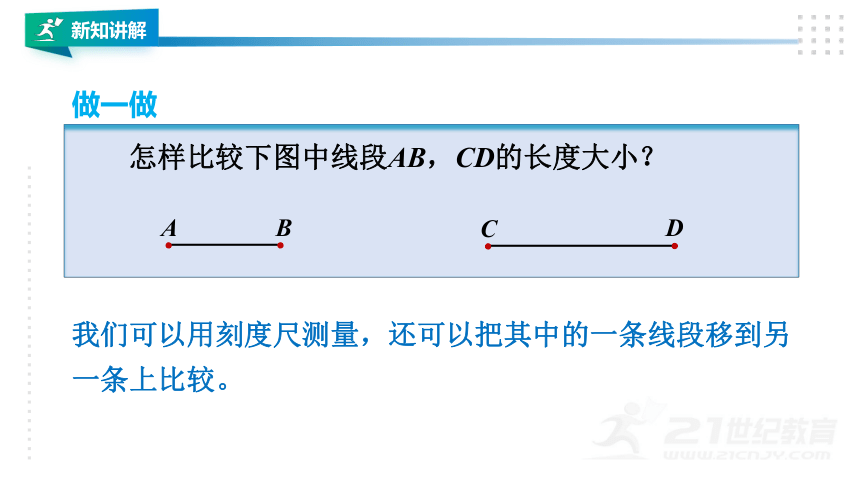
怎样比较下图中线段AB,CD的长度大小?
做一做
A
C
D
B
我们可以用刻度尺测量,还可以把其中的一条线段移到另一条上比较。
新知讲解
A
B
C
D
(A)
B
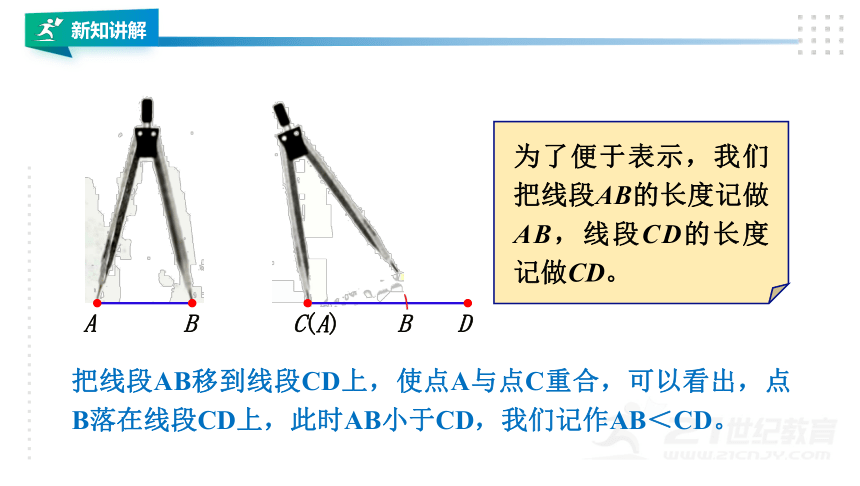
为了便于表示,我们把线段AB的长度记做AB,线段CD的长度记做CD。
把线段AB移到线段CD上,使点A与点C重合,可以看出,点B落在线段CD上,此时AB小于CD,我们记作AB<CD。
新知讲解
像上述那样,将线段AB移到CD上,使点A与点C重合,点B与点D都在点C的同侧,这时可能出现的情形如下表:
图形 线段AB与CD的关系 记做
A
B
D
C
A
B
D
C
A
B
D
C
AB小于CD
AB等于CD
AB大于CD
AB<CD
AB=CD
AB>CD
新知讲解
如图,点C落在线段AB的延长线(即以A为端点,方向为A到B的射线)上,设AB=a,AC=b,BC=c。
则:
A
B
C
记做b=a+c.
线段BC=AC-AB=b-a,即BC是b与a的差。
记做c=b-a.
线段AC=AB+BC=a+c,即AC是a与c的和。
新知讲解
做一做
杭州湾跨海大桥是跨越杭州湾的便捷通道.大桥北起嘉兴市,跨越宽阔的杭州湾海域后止于宁波市,全长36km。大桥建成后宁波至上海间的陆路距离缩短了120km.你知道这是根据什么原理吗?
新知讲解
新知讲解
过去从宁波到嘉兴的路线是:宁波→杭州→嘉兴,需绕道杭州,杭州湾跨海大桥建成后,从宁波到嘉兴的路线是:宁波→嘉兴,路线近似于一条线段,因此,从宁波到上海的陆路距离缩短了120km。
如果我们把宁波、嘉兴分别看作一个点,显然,两点之间的连线中,线段最短.
新知讲解
人们根据长期实践经验得到以下基本事实:
两点之间的所有连线中,线段最短.
简单说成:两点之间线段最短.
新知讲解
连接两点之间的线段的长度,叫做这两点间的距离.
例题讲解
例1 已知线段a,借助圆规和直尺作一条线段使它等于2a.
a
作法:
1. 作射线AD;
2. 在AD上顺次截取AB=BC=a。则AC就是所求作的线段。
B
C
a
例题讲解
像上面仅用圆规和没有刻度的直尺作图的方法叫尺规作图.
如下图,点B在线段AC上,且把线段AC分成相等的两条线段AB与BC,这时点B叫做线段AC的中点.
若点B是AC的中点,则线段AB、BC、AC的大小关系是:
例题讲解
类似地,还有线段的三等分点,四等分点,……
A
B
C
D
A
C
D
B
E
……
例题讲解
例2 如图,已知线段a,b(a>b),作一条线段使它等于a-b.
作法:
(2)在射线AF上,截取AC=a.
(3)在线段AC上,截取AB=b.
(1)作射线AF;
则线段BC就是求作的线段.
C
B
a
b
巩固练习
C
B
a
b
巩固练习
1. 如图,AB=CD,则AB与CD的大小关系是( )
A. AC>BD
B. AC<BD
C. AC=BD
D. 无法比较
C
A
B
C
D
解析:∵AB=CD,∴AB+BC=CD+BC,∴AC=BD.
巩固练习
2. 如图所示,线段AB=6cm,点C是AB的中点,点D是AC的中点,则线段DB的长为 cm.
解析:∵点C是AB的中点,点D是AC的中点,
∴
∴
巩固练习
3. 下列说法正确的是 ( )
A. 若AC=AB,则点C是AB的中点
B. 若AB=2BC,则点C是AB的中点
C. 若AB=BC,则点B是AC的中点
D. 若C是AB的中点,则AB=2AC=2BC
D
巩固练习
4. 把一段弯曲的乡村小路改修成笔直的村级公路,可以缩
短路程,运用的基本事实是 ( )
A. 两点确定一条直线
B. 两点之间线段最短
C. 经过一点有无数条直线
D. 以上三个选项都不正确
B
巩固练习
5. 如果AB=3cm,BC=5cm,那么A、B两点的距离是
( )
A. 8cm B. 2cm
C. 2cm或8cm D. 以上各项都不正确
D
巩固练习
6. 已知线段AB=14cm,直线AB上有一点C,且BC=6cm,
点P线段是AC的中点,则AP的长为 ( )
A. 4cm B. 10cm
C. 4cm或10cm D. 4cm或8cm
C
课堂总结
把AB、CD的端点A、C重合,点B、D落在点C的同侧.
1. 如何用圆规截取法,比较两条线段AB、CD的大小?
①若点B在线段CD之间,则AB<CD.
②若点B与点D重合,则AB=CD.
③若点B在线段CD的延长线上,则AB<CD.
课堂总结
如图,如果点C在线段AB上,且把线段AB分成两条相等的线段AC,CB,那么点C叫做线段AB的中点。
2. 什么叫做线段AB的中点?线段AB的中点有何性质?
性质:如果点C是线段AB的中点,则
注意:已知
不能说明点C是线段AB的中点。
A
B
C
课堂总结
3. 什么是两条线段的和?什么是两条线段的差?
如图,点A、B、C在同一条直线上,设AB=a,AC=b,BC=c.
A
B
C
则,AC是a与c的和,记做b=a+c;AB是b与c的差,记做a=b-c;BC是b与a的差,记做c=b-a.
课堂总结
4. 关于线段的基本事实是什么?
两点之间线段最短。
5. 什么叫做两点之间的距离?
连接两点的线段的长度,叫做这两点之间的距离。
作业布置
第121页课后练习第1、2、3题。
https://www.21cnjy.com/help/help_extract.php
4.2 线段、射线、直线(2)
湘教版 七年级上
教学目标
1. 理解线段大小的比较方法,知道线段比较的结果;
2. 学会线段长度,大小关系,线段和、差的表示方法;
3. 理解线段最短的基本事实及两点之间的距离的概念;
4. 学会用尺规作图方法作线段,理解线段的中点概念;
5. 进一步学会阅读几何语言,提高作图能力。
新知导入
如图,线段AB、BC、CA分别三角形中的三条边,你能解决下面问题吗?
(1)线段AB、BC、CA中,哪一条线段最长?
(2)AB、CA的长度和与线段BC的长度如何比较?
A
B
C
要解决上述问题,我们要学会用圆规等工具作图的方法,并学会线段的大小比较方法。
新知讲解
怎样比较下图中线段AB,CD的长度大小?
做一做
A
C
D
B
我们可以用刻度尺测量,还可以把其中的一条线段移到另一条上比较。
新知讲解
A
B
C
D
(A)
B
为了便于表示,我们把线段AB的长度记做AB,线段CD的长度记做CD。
把线段AB移到线段CD上,使点A与点C重合,可以看出,点B落在线段CD上,此时AB小于CD,我们记作AB<CD。
新知讲解
像上述那样,将线段AB移到CD上,使点A与点C重合,点B与点D都在点C的同侧,这时可能出现的情形如下表:
图形 线段AB与CD的关系 记做
A
B
D
C
A
B
D
C
A
B
D
C
AB小于CD
AB等于CD
AB大于CD
AB<CD
AB=CD
AB>CD
新知讲解
如图,点C落在线段AB的延长线(即以A为端点,方向为A到B的射线)上,设AB=a,AC=b,BC=c。
则:
A
B
C
记做b=a+c.
线段BC=AC-AB=b-a,即BC是b与a的差。
记做c=b-a.
线段AC=AB+BC=a+c,即AC是a与c的和。
新知讲解
做一做
杭州湾跨海大桥是跨越杭州湾的便捷通道.大桥北起嘉兴市,跨越宽阔的杭州湾海域后止于宁波市,全长36km。大桥建成后宁波至上海间的陆路距离缩短了120km.你知道这是根据什么原理吗?
新知讲解
新知讲解
过去从宁波到嘉兴的路线是:宁波→杭州→嘉兴,需绕道杭州,杭州湾跨海大桥建成后,从宁波到嘉兴的路线是:宁波→嘉兴,路线近似于一条线段,因此,从宁波到上海的陆路距离缩短了120km。
如果我们把宁波、嘉兴分别看作一个点,显然,两点之间的连线中,线段最短.
新知讲解
人们根据长期实践经验得到以下基本事实:
两点之间的所有连线中,线段最短.
简单说成:两点之间线段最短.
新知讲解
连接两点之间的线段的长度,叫做这两点间的距离.
例题讲解
例1 已知线段a,借助圆规和直尺作一条线段使它等于2a.
a
作法:
1. 作射线AD;
2. 在AD上顺次截取AB=BC=a。则AC就是所求作的线段。
B
C
a
例题讲解
像上面仅用圆规和没有刻度的直尺作图的方法叫尺规作图.
如下图,点B在线段AC上,且把线段AC分成相等的两条线段AB与BC,这时点B叫做线段AC的中点.
若点B是AC的中点,则线段AB、BC、AC的大小关系是:
例题讲解
类似地,还有线段的三等分点,四等分点,……
A
B
C
D
A
C
D
B
E
……
例题讲解
例2 如图,已知线段a,b(a>b),作一条线段使它等于a-b.
作法:
(2)在射线AF上,截取AC=a.
(3)在线段AC上,截取AB=b.
(1)作射线AF;
则线段BC就是求作的线段.
C
B
a
b
巩固练习
C
B
a
b
巩固练习
1. 如图,AB=CD,则AB与CD的大小关系是( )
A. AC>BD
B. AC<BD
C. AC=BD
D. 无法比较
C
A
B
C
D
解析:∵AB=CD,∴AB+BC=CD+BC,∴AC=BD.
巩固练习
2. 如图所示,线段AB=6cm,点C是AB的中点,点D是AC的中点,则线段DB的长为 cm.
解析:∵点C是AB的中点,点D是AC的中点,
∴
∴
巩固练习
3. 下列说法正确的是 ( )
A. 若AC=AB,则点C是AB的中点
B. 若AB=2BC,则点C是AB的中点
C. 若AB=BC,则点B是AC的中点
D. 若C是AB的中点,则AB=2AC=2BC
D
巩固练习
4. 把一段弯曲的乡村小路改修成笔直的村级公路,可以缩
短路程,运用的基本事实是 ( )
A. 两点确定一条直线
B. 两点之间线段最短
C. 经过一点有无数条直线
D. 以上三个选项都不正确
B
巩固练习
5. 如果AB=3cm,BC=5cm,那么A、B两点的距离是
( )
A. 8cm B. 2cm
C. 2cm或8cm D. 以上各项都不正确
D
巩固练习
6. 已知线段AB=14cm,直线AB上有一点C,且BC=6cm,
点P线段是AC的中点,则AP的长为 ( )
A. 4cm B. 10cm
C. 4cm或10cm D. 4cm或8cm
C
课堂总结
把AB、CD的端点A、C重合,点B、D落在点C的同侧.
1. 如何用圆规截取法,比较两条线段AB、CD的大小?
①若点B在线段CD之间,则AB<CD.
②若点B与点D重合,则AB=CD.
③若点B在线段CD的延长线上,则AB<CD.
课堂总结
如图,如果点C在线段AB上,且把线段AB分成两条相等的线段AC,CB,那么点C叫做线段AB的中点。
2. 什么叫做线段AB的中点?线段AB的中点有何性质?
性质:如果点C是线段AB的中点,则
注意:已知
不能说明点C是线段AB的中点。
A
B
C
课堂总结
3. 什么是两条线段的和?什么是两条线段的差?
如图,点A、B、C在同一条直线上,设AB=a,AC=b,BC=c.
A
B
C
则,AC是a与c的和,记做b=a+c;AB是b与c的差,记做a=b-c;BC是b与a的差,记做c=b-a.
课堂总结
4. 关于线段的基本事实是什么?
两点之间线段最短。
5. 什么叫做两点之间的距离?
连接两点的线段的长度,叫做这两点之间的距离。
作业布置
第121页课后练习第1、2、3题。
https://www.21cnjy.com/help/help_extract.php
同课章节目录
