湘教版七上数学4.3.2角的度量与计算(2)课件(共25张PPT)
文档属性
| 名称 | 湘教版七上数学4.3.2角的度量与计算(2)课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 37.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
4.3.2 角的度量与计算(2)
湘教版 七年级上
教学目标
1. 能通过实例理解余角和补角的概念;
2. 能通过合作,用等量代换推导出余角和补角的性质;
3. 学会计算图形中的角或利用方程求角;
4. 培养学生的识图能力,学会求图形中的角.
新知导入
1. 1直角等于多少度?1平角等于多少度?
1直角等于90°,1平角等于180°.
2. 什么叫作锐角?什么叫作钝角?
小于90°的角叫做锐角.
大于90°但小于180°的角叫做钝角.
3. 角的基本单位有哪些?进率是多少?
角的基本单位有度、分、秒,进率是60.
新知导入
4. 如何进行度、分、秒的单位换算?
=,=,=,=.
5. 已知∠1=34°20′,∠2=55°40′,则∠1+∠2= .
6. 已知∠A=117°15′,∠B=62°45′,则∠A+∠B= .
90°
180°
新知讲解
做一做
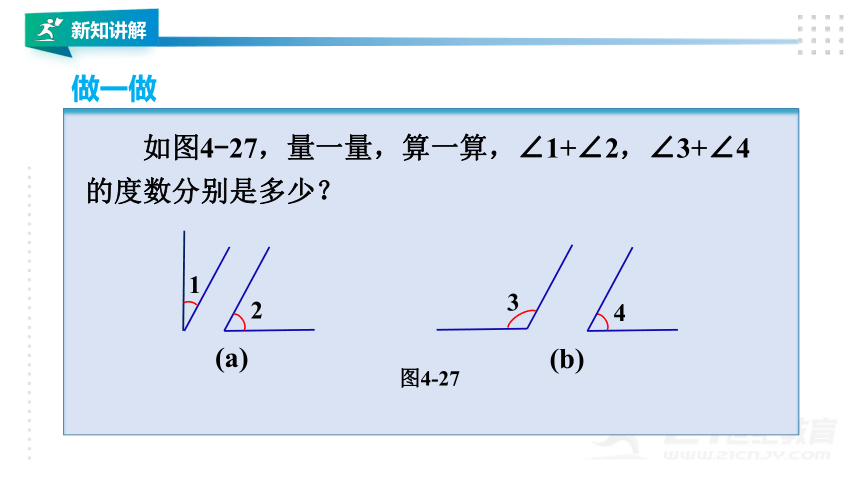
如图4-27,量一量,算一算,∠1+∠2,∠3+∠4
的度数分别是多少?
图4-27
1
2
(a)
3
4
(b)
新知讲解
在图(a)中我们量得,∠1= ,∠2= ,因此
∠1+∠2= .
30°
60°
90°
1
2
(a)
我们说∠1与∠2互为余角,也说∠1是∠2的余角,∠2是∠1的余角.
新知讲解
在图(b)中我们量得,∠3= ,∠4= ,因此
∠3+∠4= .
120°
60°
180°
3
4
(b)
我们说∠3与∠4互为补角,也说∠3是∠4的补角,∠4是∠3的补角.
新知讲解
如果两个角的和等于一个直角,那么说这两个角互为余角(简称互余),也说其中一个角是另一个角的余角.
如果两个角的和等于一个平角,那么说这两个角互为补角(简称互补),也说其中一个角是另一个角的补角.
新知讲解
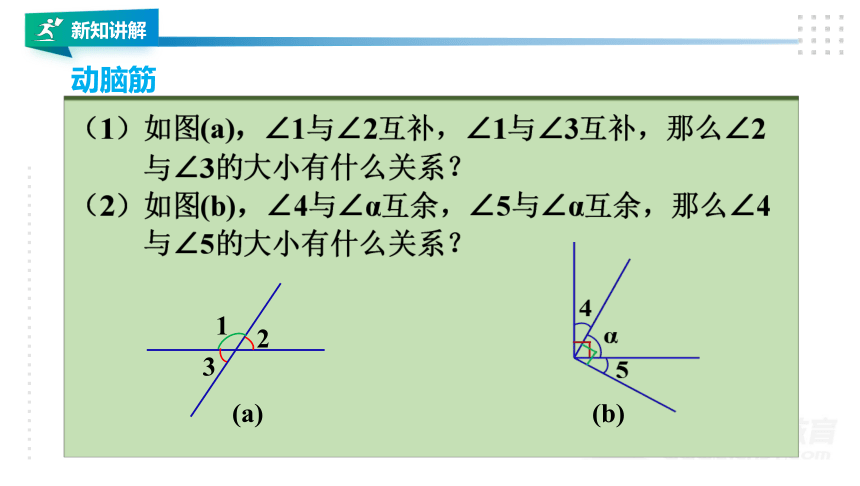
(1)如图(a),∠1与∠2互补,∠1与∠3互补,那么∠2
与∠3的大小有什么关系?
(2)如图(b),∠4与∠α互余,∠5与∠α互余,那么∠4
与∠5的大小有什么关系?
动脑筋
1
2
3
(a)
(b)
新知讲解
1
2
3
(a)
(1)如图(a),∠1与∠2互补,∠1与∠3互补,那么∠2与∠3的大小有什么关系?
因此∠2 =∠3.
由于∠1 +∠2 = 180°,∠1 +∠3 = 180°,
(等量代换)
所以∠4 =180°-∠1,∠3 =180°-∠1.
说明:等量代换是指“如果a=b且c=b,那么a=c ”.
新知讲解
(2)如图(b),∠4与∠α互余,∠5与∠α互余,那么∠4与∠5的大小有什么关系?
因此∠4 =∠5.
由于∠4+∠α =90°,∠5+∠α =90°,
(等量代换)
所以∠4 =90°-∠α,∠5 =90°-∠α.
(b)
新知讲解
于是,我们得出:
同角或等角的补角相等.
同角或等角的余角相等.
例题讲解
例4 如图,∠AOB与∠BOD互为余角,∠BOD的平分线,∠AOB=29.66°,求∠COD的度数.
A
O
B
D
C
分析:
1. 根据∠AOB与∠BOD互为余角,
∠AOB=29.66°,可求出 ;
2. 根据 ,
即可求出∠COD.
OC是∠BOD的平分线
∠BOD
例题讲解
例4 如图,∠AOB与∠BOD互为余角,∠BOD的平分线,∠AOB=29.66°,求∠COD的度数.
A
O
B
D
C
解:因为∠AOB与∠BOD互为余角,
所以∠BOD=90°-∠AOB =90°-29.66°=60.34°.
又因为OC是∠BOD的平分线,
因此,∠COD 的度数为 30.17°.
所以∠COD∠BOD
例题讲解
例5 已知一个角的余角是这个角的补角的,求这个角的度数.
分析:本题涉及等量关系:一个角的余角=这个角的补角×,因此,可设未知数列方程解答
.
解:设这个角为x°,则这个角的余角为(90-x)°,补角为(180-x)°,根据题意,得
解得
x=45 .
因此,这个角的度数为45°.
巩固练习
1. 已知∠1=40°30′20″ ,∠2是∠1的补角,∠3是∠1的余角,则∠2= , ∠3= .
49°29′40″
139°29′40″
巩固练习
2. 已知一个角的补角比这个角的余角的4倍还多15°,则这个角的度数为( )
A. 45° B. 55°
C. 65° D. 70°
C
解析:设这个角为x°,根据题意,得
解得 x=65。因此这个角为65°.
巩固练习
3. 如图,点O是直线AB上一点,∠AOD,∠COE是直
角,下列判断中错误的是( )
A. ∠AOC=∠DOE
B. ∠COD+∠AOE=180°
C. ∠COD+∠BOC=180°
D. ∠AOC+∠BOE=90°
C
A
O
B
C
D
E
巩固练习
4. 将一副三角尺按如图所示位置放置,使三角尺的直角顶点重合,当∠ACE=24°12′时,∠BCD等于 .
A
B
C
D
E
155°48′
课堂总结
1. 如果两个角的和等于一个 ,那么说这两个角互为余角,也说其中一个角是另一个角的余角.
2. 如果两个角的和等于一个 ,那么说这两个角互为补角,也说其中一个角是另一个角的补角.
直角
3. 同角或等角的补角 ,同角或等角的余角 .
平角
相等
相等
作业布置
第129页课后练习第1、2题。
1. 填空:
(1) 105°26′的补角等于 ;
(2) 28°25′32″的余角等于 .
74°34′
61°34′28″
作业布置
2. 如图,∠BOD = 118°,∠COD 是直角,OC 平分∠AOB,
求∠AOB的度数.
解:∠BOC=∠BOD-∠COD
=118°-90°=28°.
因为OC 平分∠AOB,所以
所以∠AOB=2∠BOC=2×28°=56°.
O
C
A
B
D
作业布置
第130页习题4.3第10题。
10. 如图,∠AOC和∠BOD都是直角,∠AOB∶∠AOD=
2∶11,求∠AOB和∠BOC的度数.
O
A
B
C
D
解:设∠AOB为x°,则
∠AOD=∠BOD+∠AOB=(90+x)°,
因为∠AOB∶∠AOD=2∶11,
所以x∶(90+x)=2∶11,即11x=2(90+x).
解得x=20。所以∠AOB=20°,∠BOC=70°.
https://www.21cnjy.com/help/help_extract.php
4.3.2 角的度量与计算(2)
湘教版 七年级上
教学目标
1. 能通过实例理解余角和补角的概念;
2. 能通过合作,用等量代换推导出余角和补角的性质;
3. 学会计算图形中的角或利用方程求角;
4. 培养学生的识图能力,学会求图形中的角.
新知导入
1. 1直角等于多少度?1平角等于多少度?
1直角等于90°,1平角等于180°.
2. 什么叫作锐角?什么叫作钝角?
小于90°的角叫做锐角.
大于90°但小于180°的角叫做钝角.
3. 角的基本单位有哪些?进率是多少?
角的基本单位有度、分、秒,进率是60.
新知导入
4. 如何进行度、分、秒的单位换算?
=,=,=,=.
5. 已知∠1=34°20′,∠2=55°40′,则∠1+∠2= .
6. 已知∠A=117°15′,∠B=62°45′,则∠A+∠B= .
90°
180°
新知讲解
做一做
如图4-27,量一量,算一算,∠1+∠2,∠3+∠4
的度数分别是多少?
图4-27
1
2
(a)
3
4
(b)
新知讲解
在图(a)中我们量得,∠1= ,∠2= ,因此
∠1+∠2= .
30°
60°
90°
1
2
(a)
我们说∠1与∠2互为余角,也说∠1是∠2的余角,∠2是∠1的余角.
新知讲解
在图(b)中我们量得,∠3= ,∠4= ,因此
∠3+∠4= .
120°
60°
180°
3
4
(b)
我们说∠3与∠4互为补角,也说∠3是∠4的补角,∠4是∠3的补角.
新知讲解
如果两个角的和等于一个直角,那么说这两个角互为余角(简称互余),也说其中一个角是另一个角的余角.
如果两个角的和等于一个平角,那么说这两个角互为补角(简称互补),也说其中一个角是另一个角的补角.
新知讲解
(1)如图(a),∠1与∠2互补,∠1与∠3互补,那么∠2
与∠3的大小有什么关系?
(2)如图(b),∠4与∠α互余,∠5与∠α互余,那么∠4
与∠5的大小有什么关系?
动脑筋
1
2
3
(a)
(b)
新知讲解
1
2
3
(a)
(1)如图(a),∠1与∠2互补,∠1与∠3互补,那么∠2与∠3的大小有什么关系?
因此∠2 =∠3.
由于∠1 +∠2 = 180°,∠1 +∠3 = 180°,
(等量代换)
所以∠4 =180°-∠1,∠3 =180°-∠1.
说明:等量代换是指“如果a=b且c=b,那么a=c ”.
新知讲解
(2)如图(b),∠4与∠α互余,∠5与∠α互余,那么∠4与∠5的大小有什么关系?
因此∠4 =∠5.
由于∠4+∠α =90°,∠5+∠α =90°,
(等量代换)
所以∠4 =90°-∠α,∠5 =90°-∠α.
(b)
新知讲解
于是,我们得出:
同角或等角的补角相等.
同角或等角的余角相等.
例题讲解
例4 如图,∠AOB与∠BOD互为余角,∠BOD的平分线,∠AOB=29.66°,求∠COD的度数.
A
O
B
D
C
分析:
1. 根据∠AOB与∠BOD互为余角,
∠AOB=29.66°,可求出 ;
2. 根据 ,
即可求出∠COD.
OC是∠BOD的平分线
∠BOD
例题讲解
例4 如图,∠AOB与∠BOD互为余角,∠BOD的平分线,∠AOB=29.66°,求∠COD的度数.
A
O
B
D
C
解:因为∠AOB与∠BOD互为余角,
所以∠BOD=90°-∠AOB =90°-29.66°=60.34°.
又因为OC是∠BOD的平分线,
因此,∠COD 的度数为 30.17°.
所以∠COD∠BOD
例题讲解
例5 已知一个角的余角是这个角的补角的,求这个角的度数.
分析:本题涉及等量关系:一个角的余角=这个角的补角×,因此,可设未知数列方程解答
.
解:设这个角为x°,则这个角的余角为(90-x)°,补角为(180-x)°,根据题意,得
解得
x=45 .
因此,这个角的度数为45°.
巩固练习
1. 已知∠1=40°30′20″ ,∠2是∠1的补角,∠3是∠1的余角,则∠2= , ∠3= .
49°29′40″
139°29′40″
巩固练习
2. 已知一个角的补角比这个角的余角的4倍还多15°,则这个角的度数为( )
A. 45° B. 55°
C. 65° D. 70°
C
解析:设这个角为x°,根据题意,得
解得 x=65。因此这个角为65°.
巩固练习
3. 如图,点O是直线AB上一点,∠AOD,∠COE是直
角,下列判断中错误的是( )
A. ∠AOC=∠DOE
B. ∠COD+∠AOE=180°
C. ∠COD+∠BOC=180°
D. ∠AOC+∠BOE=90°
C
A
O
B
C
D
E
巩固练习
4. 将一副三角尺按如图所示位置放置,使三角尺的直角顶点重合,当∠ACE=24°12′时,∠BCD等于 .
A
B
C
D
E
155°48′
课堂总结
1. 如果两个角的和等于一个 ,那么说这两个角互为余角,也说其中一个角是另一个角的余角.
2. 如果两个角的和等于一个 ,那么说这两个角互为补角,也说其中一个角是另一个角的补角.
直角
3. 同角或等角的补角 ,同角或等角的余角 .
平角
相等
相等
作业布置
第129页课后练习第1、2题。
1. 填空:
(1) 105°26′的补角等于 ;
(2) 28°25′32″的余角等于 .
74°34′
61°34′28″
作业布置
2. 如图,∠BOD = 118°,∠COD 是直角,OC 平分∠AOB,
求∠AOB的度数.
解:∠BOC=∠BOD-∠COD
=118°-90°=28°.
因为OC 平分∠AOB,所以
所以∠AOB=2∠BOC=2×28°=56°.
O
C
A
B
D
作业布置
第130页习题4.3第10题。
10. 如图,∠AOC和∠BOD都是直角,∠AOB∶∠AOD=
2∶11,求∠AOB和∠BOC的度数.
O
A
B
C
D
解:设∠AOB为x°,则
∠AOD=∠BOD+∠AOB=(90+x)°,
因为∠AOB∶∠AOD=2∶11,
所以x∶(90+x)=2∶11,即11x=2(90+x).
解得x=20。所以∠AOB=20°,∠BOC=70°.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
