湘教版2021-2022学年数学八年级上册 期末模拟练习1(含解析)
文档属性
| 名称 | 湘教版2021-2022学年数学八年级上册 期末模拟练习1(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-28 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
湘教版八年级2021-2022期末模拟练习1
姓名:__________班级:__________考号:__________总分__________
1 、选择题(本大题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
4 的平方根是( )
A.2 B.-2 C.±2 D.±4
(2017年四川省眉山市 )已知m2+n2=n﹣m﹣2,则﹣的值等于( )
A.1 B.0 C.﹣1 D.﹣
(2019年广西南宁市、北部湾经济区、北海市、崇左市、防城港市、钦州市)将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( )
A.60° B.65° C.75° D.85°
如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=35°,则∠EAC的度数为( )
A. 40° B. 35° C. 30° D. 25°
(2017年山东滨州市)如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为( )
A.40° B.36° C.30° D.25°
(2020年四川省雅安市)不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
(2017年山东枣庄市)实数a,b在数轴上对应点的位置如图所示,化简|a|+的结果是( )
A.﹣2a+b B.2a﹣b C.﹣b D.b
(2021年青海)如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
A.7.5 B.8 C.15 D.无法确定
(2020年湖北省荆门市)中,,D为的中点,,则的面积为( )
A. B. C. D.
(2019年重庆市(b卷))若数使关于的不等式组有且仅有三个整数解,且使关于的分式方程的解为正数,则所有满足条件的整数的值之和是( )
A. B. C. D.1
1 、填空题(本大题共8小题,每小题3分,共24分)
(2021年山东省临沂市)比较大小:___5(选填“”、“ ”、“ ” ).
(2020年山东省济宁市)已知三角形的两边长分别为3和6,则这个三角形的第三边长可以是__________(写出一个即可),
(2017年广西百色市 )下列四个命题中:①对顶角相等;②同旁内角互补;③全等三角形的对应角相等;④两直线平行,同位角相等,其中假命题的有 (填序号)
(2014-2015学年湖北省襄阳市八年级上期末数学试卷)等腰三角形的周长为16,其一边长为6,则另两边的长为__________
(2021年内蒙古鄂尔多斯)计算:___________.
(2020年湖南省常德市)计算:﹣=_____.
等腰三角形一腰上的高与另一腰的夹角为40°,则这个等腰三角形的一个底角的度数为 .
(2020年四川省遂宁市)若关于x的不等式组有且只有三个整数解,则m的取值范围是______.
1 、解答题(本大题共8小题,共66分)
(2015年辽宁省锦州市) 先化简,再求值:(1+)÷,其中:x=3﹣3.
(2017年浙江省义乌市 )(1)计算:(2﹣π)0+|4﹣3|﹣.
(2)解不等式:4x+5≤2(x+1)
解答下列各题:
(1)计算:①; ②;
(2)求下列各式中的实数:
①; ②
(2018年四川省攀枝花市)攀枝花市出租车的收费标准是:起步价5元(即行驶距离不超过2千米都需付5元车费),超过2千米以后,每增加1千米,加收1.8元(不足1千米按1千米计).某同学从家乘出租车到学校,付了车费24.8元.求该同学的家到学校的距离在什么范围?
如图,在△ABE中,AD⊥BE于点D,C是BE上一点,BD=DC,且点C在AE的垂直平分线上,若△ABC的周长为18 cm,求DE的长.
(2017年贵州省毕节地区 )某同学准备购买笔和本子送给农村希望小学的同学,在市场上了解到某种本子的单价比某种笔的单价少4元,且用30元买这种本子的数量与用50元买这种笔的数量相同
(1)求这种笔和本子的单价;
(2)该同学打算用自己的100元压岁钱购买这种笔和本子,计划100元刚好用完,并且笔和本子都买,请列出所有购买方案.
如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M.
(1)若∠B=70°,则∠NMA的度数是 ;
(2)探究∠B与∠NMA的关系,并说明理由;
(3)连接MB,若AB=8cm,△MBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在点P,使PB+CP的值最小?若存在,标出点P的位置并求PB+CP的最小值;若不存在,说明理由.
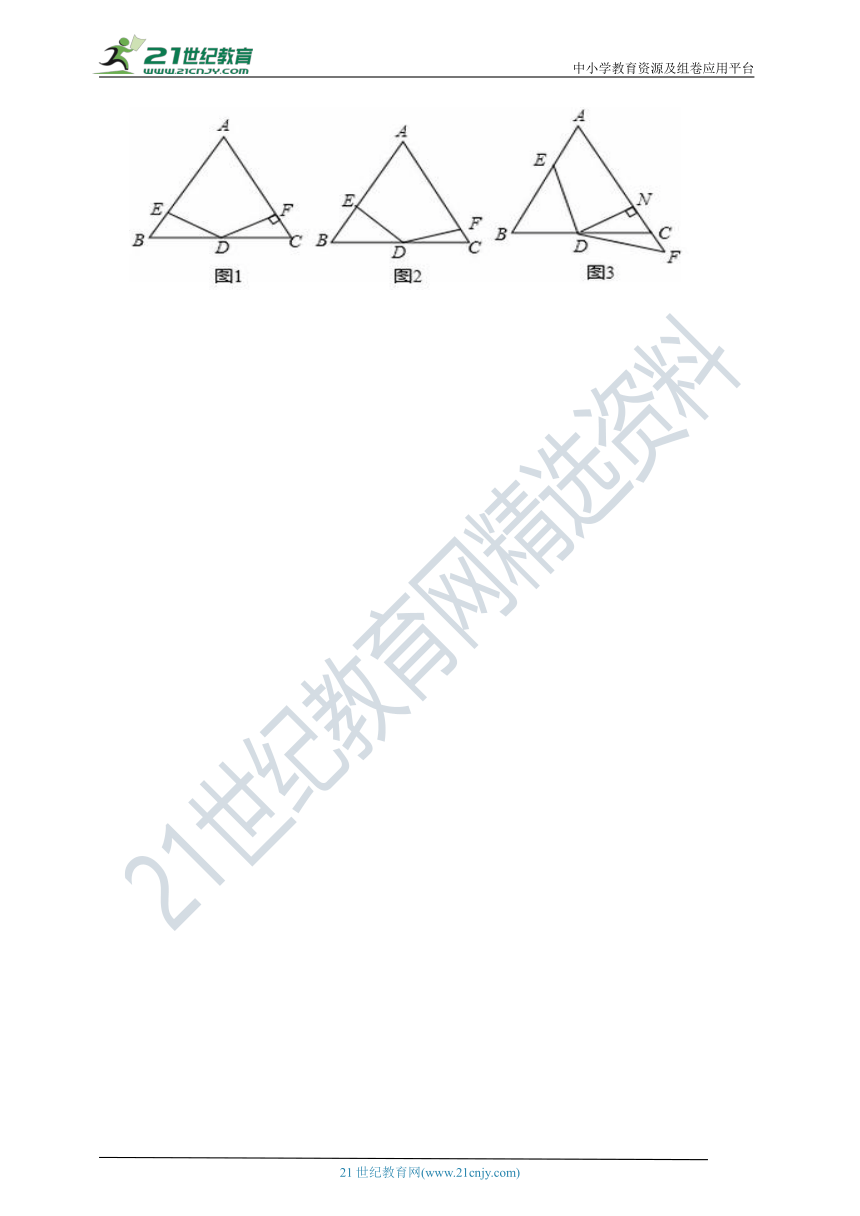
在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.求证:BE+CE=AB;
(3)如图3,将(2)中的∠EDF继续绕点D顺时针旋转一定的角度,使DF与线段AC的延长线交与点F,作DN⊥AC于点N,若DN=FN,求证:BE+CE=(BE-CF).
答案解析
1 、选择题
【考点】平方根
【分析】根据平方根的定义,求数a的平方根,也就是求一个数x,使得x2=a,则x就是a的平方根,由此即可解决问题.
解:,则4的平方根是,
故选择:C.
【点评】本题考查了平方根的定义.注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.
【考点】 分式的化简求值.
【分析】把所给等式整理为2个完全平方式的和为0的形式,得到m,n的值,代入求值即可.
解:由m2+n2=n﹣m﹣2,得
(m+2)2+(n﹣2)2=0,
则m=﹣2,n=2,
∴﹣=﹣﹣=﹣1.
故选:C.
【点评】考查分式的化简求值,把所给等式整理为2个完全平方式的和为0的形式是解决本题的突破点;用到的知识点为:2个完全平方式的和为0,这2个完全平方式的底数为0.
【考点】平行线的性质,三角形的外角性质
【分析】利用三角形外角性质(三角形的一个外角等于不相邻的两个内角和)解题或利用三角形内角和解题皆可.
解:如图:
∵∠BCA=60°,∠DCE=45°,
∴∠2=180°﹣60°﹣45°=75°,
∵HF∥BC,
∴∠1=∠2=75°,
故选:C.
【点评】主要考查了一副三角板所对应的角度是60°,45°,30°,90°和三角形外角的性质.本题容易,解法很灵活.
【考点】全等三角形的性质.
【分析】根据三角形的内角和定理列式求出∠BAC,再根据全等三角形对应角相等可得∠DAE=∠BAC,然后根据∠EAC=∠DAE﹣∠DAC代入数据进行计算即可得解.
解:∵∠B=80°,∠C=30°,
∴∠BAC=180°﹣80°﹣30°=70°,
∵△ABC≌△ADE,
∴∠DAE=∠BAC=70°,
∴∠EAC=∠DAE﹣∠DAC,
=70°﹣35°,
=35°.
故选B.
【点评】本题考查了全等三角形对应角相等的性质,熟记性质并准确识图是解题的关键.
【考点】等腰三角形的性质.
【分析】根据AB=AC可得∠B=∠C,CD=DA可得∠ADB=2∠C=2∠B,BA=BD,可得∠BDA=∠BAD=2∠B,在△ABD中利用三角形内角和定理可求出∠B.
解:∵AB=AC,
∴∠B=∠C,
∵CD=DA,
∴∠C=∠DAC,
∵BA=BD,
∴∠BDA=∠BAD=2∠C=2∠B,
设∠B=α,
则∠BDA=∠BAD=2α,
又∵∠B+∠BAD+∠BDA=180°,
∴α+2α+2α=180°,
∴α=36°,
∴∠B=36°,
故选B.
【点评】本题主要考查等腰三角形的性质,掌握等边对等角是解题的关键,注意三角形内角和定理和方程思想的应用.
【考点】在数轴上表示不等式的解集
【分析】先得出不等式组的解集,再找到对应的数轴表示即可.
解:由题意可得:
不等式组的解集为:-2≤x<1,
在数轴上表示为:
故选A.
【点评】此题主要考查了不等式组解集在数轴上的表示方法:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.
【考点】二次根式的性质与化简;实数与数轴.
【分析】直接利用数轴上a,b的位置,进而得出a<0,a﹣b<0,再利用绝对值以及二次根式的性质化简得出答案.
解:由图可知:a<0,a﹣b<0,
则|a|+
=﹣a﹣(a﹣b)
=﹣2a+b.
故选:A.
【点评】此题主要考查了二次根式的性质以及实数与数轴,正确得出各项符号是解题关键.
【考点】角平分线的性质
【分析】过D点作DE⊥BC于E,如图,根据角平分线的性质得到DE=DA=3,然后根据三角形面积公式计算.
解:如图,过点D作DE⊥BC于点E.
∵∠A=90°,
∴AD⊥AB.
∴AD=DE=3.
又∵BC=5,
∴S△BCD=BC DE=×5×3=7.5.
故选A.
【点评】本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等
【考点】等腰三角形的性质
【分析】连接AD,用等腰三角形的“三线合一”,得到的度数,及,由得,得,计算的面积即可.
解:连接AD,如图所示:
∵,且D为BC中点
∴,且,
∴中,
∵
∴
∴
故选:B.
【点评】本题考查了等腰三角形的性质,及解直角三角形和三角形面积的计算,熟知以上知识是解题的关键.
【考点】解一元一次不等式,分式方程的解,一元一次不等式组的整数解
【分析】先解不等式组根据其有三个整数解,得的一个范围;再解关于的分式方程,根据其解为正数,并考虑增根的情况,再得的一个范围,两个范围综合考虑,则所有满足条件的整数的值可求,从而得其和.
解:由关于的不等式组得
有且仅有三个整数解,
,,2,或3.
,
;
由关于的分式方程得,
,
解为正数,且为增根,
,且,
,且,
所有满足条件的整数的值为:,,0,其和为.
故选:.
【点评】本题属于含参一元一次不等式组和含参分式方程的综合计算题,比较容易错,属于易错题.
1 、填空题
【考点】实数的大小的比较
【分析】先把两数值化成带根号的形式,再根据实数的大小比较方法即可求解.
解:∵,,
而24<25,
∴<5.
故答案为:<.
【点评】此题主要考查了实数的大小的比较,当一个带根号的无理数和一个有理数进行比较时,首选的方法就是把它们还原成带根号的形式,然后比较被开方数即可解决问题.
【考点】三角形三边的关系
【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于三边”,求得第三边的取值范围,即可得出结果.
解:根据三角形的三边关系,得:
第三边应大于6-3=3,而小于6+3=9,
故第三边的长度3<x<9.
故答案为:4(答案不唯一,在3<x<9之内皆可).
【点评】此题主要考查了三角形的三边关系,根据三角形三边关系定理列出不等式,然后解不等式,确定取值范围即可.
【考点】命题与定理.
【分析】要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.
解:①对顶角相等是真命题;
②同旁内角互补是假命题;
③全等三角形的对应角相等是真命题;
④两直线平行,同位角相等是真命题;
故假命题有②,
故答案为:②.
【点评】本题主要考查了命题与定理的运用,解题时注意:命题的“真”“假”是就命题的内容而言,任何一个命题非真即假.
【考点】等腰三角形的性质;三角形三边关系.
【分析】分腰长为6和底边为6,求出其另外两边,再利用三角形的三边关系进行验证即可.
解:当腰为6时,则另两边长为6、4,此时三边满足三角形三边关系;
当底边为6时,则另两边长为5、5,此时三边满足三角形三边关系;
故答案为:6,4或5,5.
【点评】本题考查了等腰三角形的性质及三角形的三边关系,解题的关键是能够分类讨论,难度不大.
【考点】立方根,零指数幂,负整数指数幂
【分析】根据立方根、零指数幂、负整数指数幂的运算法则即可求解.
解:原式=
故答案为:-4
【点评】本题考查了立方根、零指数幂、负整数指数幂、实数的混合运算等知识点,熟知上述的各种运算法则是解题的基础.
【考点】二次根式的混合运算
【分析】直接化简二次根式进而合并得出答案.
解:原式=﹣+2
=3.
故答案为:3.
【点评】本题主要考查了二次根式的混合运算,正确化简二次根式是解答的关键.
【考点】等腰三角形的性质;三角形内角和定理.
【分析】本题已知没有明确三角形的类型,所以应分这个等腰三角形是锐角三角形和钝角三角形两种情况讨论.
解:当这个三角形是锐角三角形时:高与另一腰的夹角为40,则顶角是50°,因而底角是65°;
如图所示:当这个三角形是钝角三角形时:∠ABD=50°,BD⊥CD,
故∠BAD=50°,
所以∠B=∠C=25°
因此这个等腰三角形的一个底角的度数为25°或65°.
故填25°或65°.
【点评】本题考查了等腰三角形的性质及三角形内角和定理;等腰三角形的高线,可能在三角形的内部,边上、外部几种不同情况,因而,遇到与等腰三角形的高有关的计算时应分类讨论.
【考点】一元一次不等式组的整数解
【分析】解不等式组得出其解集为﹣2<x≤,根据不等式组有且只有三个整数解得出1≤<2,解之可得答案.
解:解不等式,得:x>﹣2,
解不等式2x﹣m≤2﹣x,得:x≤,
则不等式组的解集为﹣2<x≤,
∵不等式组有且只有三个整数解,
∴1≤<2,
解得:1≤m<4,
故答案为:1≤m<4.
【点评】本题考查了不等式组的整数解,关键是根据不等式组的整数解求出取值范围,用到的知识点是一元一次不等式的解法.
1 、解答题
【考点】分式的化简求值.
【分析】原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解:原式=
=
=x+1,
当x=3﹣3时,原式=3﹣3+1=3﹣2.
【点评】此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.
【考点】解一元一次不等式;实数的运算;零指数幂.
【分析】(1)原式利用零指数幂法则,绝对值的代数意义,以及二次根式性质计算即可得到结果;
(2)去括号,移项,合并同类项,系数化成1即可求出不等式的解集.
解:(1)原式=1
=﹣3;
(2)去括号,得4x+5≤2x+2
移项合并同类项得,2x≤﹣3
解得x.
【点评】此题考查了实数的运算和一元一次不等式的运算,零指数幂、负整数指数幂,熟练拿握运算法则是解本题的关键。
【考点】二次根式的混合运算,求一个数的立方根
【分析】(1)①从左往右依次计算开平方、乘方、开立方、约分,再计算加减即可;
②先去括号和绝对值,再计算加减即可;
(2)①根据绝对值的性质直接去绝对值即可;
②利用立方根的性质计算即可.
解:(1)①原式
②原式
(2)①
②
【点评】本题考查了二次根式的混合运算、求绝对值、求一个数的立方根,熟练掌握运算法则是解题的关键.
【考点】一元一次不等式组的应用
【分析】已知该同学的家到学校共需支付车费24.8元,从同学的家到学校的距离为x千米,首先去掉前2千米的费用,从而根据题意列出不等式,从而得出答案.
解:设该同学的家到学校的距离是x千米,依题意:
13.8﹣1.8<5+1.8(x﹣2)≤24.8,
解得:12<x≤13.
故该同学的家到学校的距离在大于12小于等于13的范围.
【点评】此题主要考查了一元一次不等式的应用,根据题意明确其收费标准分两部分是完成本题的关键.
【考点】线段垂直平分线的性质
【分析】根据线段垂直平分线的性质得到CA=CE,AB=AC,根据三角形的周长公式计算,得到答案.
解:∵点C在AE的垂直平分线上,
∴CA=CE,
∵AD⊥BE,BD=DC,
∴AB=AC,
∵△ABC的周长为18,
∴AB+BC+AC=18,
∴2AC+2DC=18,
∴AC+DC=9,
∴DE=DC+CE=AC+CD=9(cm).
【点评】本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
【考点】分式方程的应用;二元一次方程的应用.
【分析】(1)首先设这种笔单价为x元,则本子单价为(x﹣4)元,根据题意可得等量关系:30元买这种本子的数量=50元买这种笔的数量,由等量关系可得方程=,再解方程可得答案;
(2)设恰好用完100元,可购买这种笔m支和购买本子n本,根据题意可得这种笔的单价×这种笔的支数m+本子的单价×本子的本数n=1000,再求出整数解即可.
解:(1)设这种笔单价为x元,则本子单价为(x﹣4)元,由题意得:
=,
解得:x=10,
经检验:x=10是原分式方程的解,
则x﹣4=6.
答:这种笔单价为10元,则本子单价为6元;
(2)设恰好用完100元,可购买这种笔m支和购买本子n本,
由题意得:10m+6n=100,
整理得:m=10﹣n,
∵m、n都是正整数,
∴①n=5时,m=7,②n=10时,m=4,③n=15,m=1;
∴有三种方案:
①购买这种笔7支,购买本子5本;
②购买这种笔4支,购买本子10本;
③购买这种笔1支,购买本子15本.
【点评】此题主要考查了分式方程和二元一次方程的应用,关键是正确理解题意,找出题目中的等量关系,列出方程.
【考点】轴对称-最短路线问题;线段垂直平分线的性质;等腰三角形的性质.
【分析】(1)根据等腰三角的性质,三角形的内角和定理,可得∠A的度数,根据直角三角形两锐角的关系,可得答案;
(2)根据等腰三角的性质,三角形的内角和定理,可得∠A的度数,根据直角三角形两锐角的关系,可得答案;
(3)根据垂直平分线的性质,可得AM与MB的关系,再根据三角形的周长,可得答案;根据两点之间线段最短,可得P点与M点的关系,可得PB+PC与AC的关系.
解:(1)若∠B=70°,则∠NMA的度数是 50°,
故答案为:50°;
(2)猜想的结论为:∠NMA=2∠B﹣90°.
理由:∵AB=AC,
∴∠B=∠C,
∴∠A=180°﹣2∠B,
又∵MN垂直平分AB,
∴∠NMA=90°﹣∠A=90°﹣(180°﹣2∠B)=2∠B﹣90°.
(3)如图:
①∵MN垂直平分AB.
∴MB=MA,
又∵△MBC的周长是14cm,
∴AC+BC=14cm,
∴BC=6cm.
②当点P与点M重合时,PB+CP的值最小,最小值是8cm.
【点评】本题考查了轴对称,线段垂直平分线上的点到线段两端点的距离相等得出PB=PA.
【考点】全等三角形的判定好性质,多边形内角和,直角三角形的性质
【分析】根据四边形的内角和定理得出DE⊥AB,从而得到BE的长度;取AB的中点G,连接DG,得出DG为△ABC的中位线,则DG=DC,∠BGD=∠C=60°,根据四边形对角互补得出∠GED=∠DFC,从而得到△DEG和△DFC全等,得到EG=CF,得出答案;取AB的中点G,连接DG,同⑵,易证△DEG≌△DFC得出EG=CF,设CN=x,根据Rt△DCN得出CD=2x,DN=x,根据题意得出EG、BE与x的关系,从而进行说明.
解:⑴由四边形AEDF的内角和为360°,可知DE⊥AB,故BE=2
⑵取AB的中点G,连接DG
易证:DG为△ABC的中位线,故DG=DC,∠BGD=∠C=60°
又四边形AEDF的对角互补,故∠GED=∠DFC
∴△DEG≌△DFC
故EG=CF
∴BE+CF=BE+EG=BG=AB
⑶取AB的中点G,连接DG
同⑵,易证△DEG≌△DFC
故EG=CF
故BE-CF=BE-EG=BG=AB
设CN=x
在Rt△DCN中,CD=2x,DN=x
在RT△DFN中,NF=DN=x,故EG=CF=(-1)x
BE=BG+EG=DC+CF=2x+(-1)x =(+1)x
故BE+CF=(+1)x+(-1)x=2x,
(BE-CF)=[(+1) x-(-1)x]= 2x.
故.
【点评】本题主要考查了等边三角形的判定与性质、四边形的内角和定理、全等三角形的判定与性质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
湘教版八年级2021-2022期末模拟练习1
姓名:__________班级:__________考号:__________总分__________
1 、选择题(本大题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
4 的平方根是( )
A.2 B.-2 C.±2 D.±4
(2017年四川省眉山市 )已知m2+n2=n﹣m﹣2,则﹣的值等于( )
A.1 B.0 C.﹣1 D.﹣
(2019年广西南宁市、北部湾经济区、北海市、崇左市、防城港市、钦州市)将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( )
A.60° B.65° C.75° D.85°
如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=35°,则∠EAC的度数为( )
A. 40° B. 35° C. 30° D. 25°
(2017年山东滨州市)如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为( )
A.40° B.36° C.30° D.25°
(2020年四川省雅安市)不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
(2017年山东枣庄市)实数a,b在数轴上对应点的位置如图所示,化简|a|+的结果是( )
A.﹣2a+b B.2a﹣b C.﹣b D.b
(2021年青海)如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
A.7.5 B.8 C.15 D.无法确定
(2020年湖北省荆门市)中,,D为的中点,,则的面积为( )
A. B. C. D.
(2019年重庆市(b卷))若数使关于的不等式组有且仅有三个整数解,且使关于的分式方程的解为正数,则所有满足条件的整数的值之和是( )
A. B. C. D.1
1 、填空题(本大题共8小题,每小题3分,共24分)
(2021年山东省临沂市)比较大小:___5(选填“”、“ ”、“ ” ).
(2020年山东省济宁市)已知三角形的两边长分别为3和6,则这个三角形的第三边长可以是__________(写出一个即可),
(2017年广西百色市 )下列四个命题中:①对顶角相等;②同旁内角互补;③全等三角形的对应角相等;④两直线平行,同位角相等,其中假命题的有 (填序号)
(2014-2015学年湖北省襄阳市八年级上期末数学试卷)等腰三角形的周长为16,其一边长为6,则另两边的长为__________
(2021年内蒙古鄂尔多斯)计算:___________.
(2020年湖南省常德市)计算:﹣=_____.
等腰三角形一腰上的高与另一腰的夹角为40°,则这个等腰三角形的一个底角的度数为 .
(2020年四川省遂宁市)若关于x的不等式组有且只有三个整数解,则m的取值范围是______.
1 、解答题(本大题共8小题,共66分)
(2015年辽宁省锦州市) 先化简,再求值:(1+)÷,其中:x=3﹣3.
(2017年浙江省义乌市 )(1)计算:(2﹣π)0+|4﹣3|﹣.
(2)解不等式:4x+5≤2(x+1)
解答下列各题:
(1)计算:①; ②;
(2)求下列各式中的实数:
①; ②
(2018年四川省攀枝花市)攀枝花市出租车的收费标准是:起步价5元(即行驶距离不超过2千米都需付5元车费),超过2千米以后,每增加1千米,加收1.8元(不足1千米按1千米计).某同学从家乘出租车到学校,付了车费24.8元.求该同学的家到学校的距离在什么范围?
如图,在△ABE中,AD⊥BE于点D,C是BE上一点,BD=DC,且点C在AE的垂直平分线上,若△ABC的周长为18 cm,求DE的长.
(2017年贵州省毕节地区 )某同学准备购买笔和本子送给农村希望小学的同学,在市场上了解到某种本子的单价比某种笔的单价少4元,且用30元买这种本子的数量与用50元买这种笔的数量相同
(1)求这种笔和本子的单价;
(2)该同学打算用自己的100元压岁钱购买这种笔和本子,计划100元刚好用完,并且笔和本子都买,请列出所有购买方案.
如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M.
(1)若∠B=70°,则∠NMA的度数是 ;
(2)探究∠B与∠NMA的关系,并说明理由;
(3)连接MB,若AB=8cm,△MBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在点P,使PB+CP的值最小?若存在,标出点P的位置并求PB+CP的最小值;若不存在,说明理由.
在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.求证:BE+CE=AB;
(3)如图3,将(2)中的∠EDF继续绕点D顺时针旋转一定的角度,使DF与线段AC的延长线交与点F,作DN⊥AC于点N,若DN=FN,求证:BE+CE=(BE-CF).
答案解析
1 、选择题
【考点】平方根
【分析】根据平方根的定义,求数a的平方根,也就是求一个数x,使得x2=a,则x就是a的平方根,由此即可解决问题.
解:,则4的平方根是,
故选择:C.
【点评】本题考查了平方根的定义.注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.
【考点】 分式的化简求值.
【分析】把所给等式整理为2个完全平方式的和为0的形式,得到m,n的值,代入求值即可.
解:由m2+n2=n﹣m﹣2,得
(m+2)2+(n﹣2)2=0,
则m=﹣2,n=2,
∴﹣=﹣﹣=﹣1.
故选:C.
【点评】考查分式的化简求值,把所给等式整理为2个完全平方式的和为0的形式是解决本题的突破点;用到的知识点为:2个完全平方式的和为0,这2个完全平方式的底数为0.
【考点】平行线的性质,三角形的外角性质
【分析】利用三角形外角性质(三角形的一个外角等于不相邻的两个内角和)解题或利用三角形内角和解题皆可.
解:如图:
∵∠BCA=60°,∠DCE=45°,
∴∠2=180°﹣60°﹣45°=75°,
∵HF∥BC,
∴∠1=∠2=75°,
故选:C.
【点评】主要考查了一副三角板所对应的角度是60°,45°,30°,90°和三角形外角的性质.本题容易,解法很灵活.
【考点】全等三角形的性质.
【分析】根据三角形的内角和定理列式求出∠BAC,再根据全等三角形对应角相等可得∠DAE=∠BAC,然后根据∠EAC=∠DAE﹣∠DAC代入数据进行计算即可得解.
解:∵∠B=80°,∠C=30°,
∴∠BAC=180°﹣80°﹣30°=70°,
∵△ABC≌△ADE,
∴∠DAE=∠BAC=70°,
∴∠EAC=∠DAE﹣∠DAC,
=70°﹣35°,
=35°.
故选B.
【点评】本题考查了全等三角形对应角相等的性质,熟记性质并准确识图是解题的关键.
【考点】等腰三角形的性质.
【分析】根据AB=AC可得∠B=∠C,CD=DA可得∠ADB=2∠C=2∠B,BA=BD,可得∠BDA=∠BAD=2∠B,在△ABD中利用三角形内角和定理可求出∠B.
解:∵AB=AC,
∴∠B=∠C,
∵CD=DA,
∴∠C=∠DAC,
∵BA=BD,
∴∠BDA=∠BAD=2∠C=2∠B,
设∠B=α,
则∠BDA=∠BAD=2α,
又∵∠B+∠BAD+∠BDA=180°,
∴α+2α+2α=180°,
∴α=36°,
∴∠B=36°,
故选B.
【点评】本题主要考查等腰三角形的性质,掌握等边对等角是解题的关键,注意三角形内角和定理和方程思想的应用.
【考点】在数轴上表示不等式的解集
【分析】先得出不等式组的解集,再找到对应的数轴表示即可.
解:由题意可得:
不等式组的解集为:-2≤x<1,
在数轴上表示为:
故选A.
【点评】此题主要考查了不等式组解集在数轴上的表示方法:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.
【考点】二次根式的性质与化简;实数与数轴.
【分析】直接利用数轴上a,b的位置,进而得出a<0,a﹣b<0,再利用绝对值以及二次根式的性质化简得出答案.
解:由图可知:a<0,a﹣b<0,
则|a|+
=﹣a﹣(a﹣b)
=﹣2a+b.
故选:A.
【点评】此题主要考查了二次根式的性质以及实数与数轴,正确得出各项符号是解题关键.
【考点】角平分线的性质
【分析】过D点作DE⊥BC于E,如图,根据角平分线的性质得到DE=DA=3,然后根据三角形面积公式计算.
解:如图,过点D作DE⊥BC于点E.
∵∠A=90°,
∴AD⊥AB.
∴AD=DE=3.
又∵BC=5,
∴S△BCD=BC DE=×5×3=7.5.
故选A.
【点评】本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等
【考点】等腰三角形的性质
【分析】连接AD,用等腰三角形的“三线合一”,得到的度数,及,由得,得,计算的面积即可.
解:连接AD,如图所示:
∵,且D为BC中点
∴,且,
∴中,
∵
∴
∴
故选:B.
【点评】本题考查了等腰三角形的性质,及解直角三角形和三角形面积的计算,熟知以上知识是解题的关键.
【考点】解一元一次不等式,分式方程的解,一元一次不等式组的整数解
【分析】先解不等式组根据其有三个整数解,得的一个范围;再解关于的分式方程,根据其解为正数,并考虑增根的情况,再得的一个范围,两个范围综合考虑,则所有满足条件的整数的值可求,从而得其和.
解:由关于的不等式组得
有且仅有三个整数解,
,,2,或3.
,
;
由关于的分式方程得,
,
解为正数,且为增根,
,且,
,且,
所有满足条件的整数的值为:,,0,其和为.
故选:.
【点评】本题属于含参一元一次不等式组和含参分式方程的综合计算题,比较容易错,属于易错题.
1 、填空题
【考点】实数的大小的比较
【分析】先把两数值化成带根号的形式,再根据实数的大小比较方法即可求解.
解:∵,,
而24<25,
∴<5.
故答案为:<.
【点评】此题主要考查了实数的大小的比较,当一个带根号的无理数和一个有理数进行比较时,首选的方法就是把它们还原成带根号的形式,然后比较被开方数即可解决问题.
【考点】三角形三边的关系
【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于三边”,求得第三边的取值范围,即可得出结果.
解:根据三角形的三边关系,得:
第三边应大于6-3=3,而小于6+3=9,
故第三边的长度3<x<9.
故答案为:4(答案不唯一,在3<x<9之内皆可).
【点评】此题主要考查了三角形的三边关系,根据三角形三边关系定理列出不等式,然后解不等式,确定取值范围即可.
【考点】命题与定理.
【分析】要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.
解:①对顶角相等是真命题;
②同旁内角互补是假命题;
③全等三角形的对应角相等是真命题;
④两直线平行,同位角相等是真命题;
故假命题有②,
故答案为:②.
【点评】本题主要考查了命题与定理的运用,解题时注意:命题的“真”“假”是就命题的内容而言,任何一个命题非真即假.
【考点】等腰三角形的性质;三角形三边关系.
【分析】分腰长为6和底边为6,求出其另外两边,再利用三角形的三边关系进行验证即可.
解:当腰为6时,则另两边长为6、4,此时三边满足三角形三边关系;
当底边为6时,则另两边长为5、5,此时三边满足三角形三边关系;
故答案为:6,4或5,5.
【点评】本题考查了等腰三角形的性质及三角形的三边关系,解题的关键是能够分类讨论,难度不大.
【考点】立方根,零指数幂,负整数指数幂
【分析】根据立方根、零指数幂、负整数指数幂的运算法则即可求解.
解:原式=
故答案为:-4
【点评】本题考查了立方根、零指数幂、负整数指数幂、实数的混合运算等知识点,熟知上述的各种运算法则是解题的基础.
【考点】二次根式的混合运算
【分析】直接化简二次根式进而合并得出答案.
解:原式=﹣+2
=3.
故答案为:3.
【点评】本题主要考查了二次根式的混合运算,正确化简二次根式是解答的关键.
【考点】等腰三角形的性质;三角形内角和定理.
【分析】本题已知没有明确三角形的类型,所以应分这个等腰三角形是锐角三角形和钝角三角形两种情况讨论.
解:当这个三角形是锐角三角形时:高与另一腰的夹角为40,则顶角是50°,因而底角是65°;
如图所示:当这个三角形是钝角三角形时:∠ABD=50°,BD⊥CD,
故∠BAD=50°,
所以∠B=∠C=25°
因此这个等腰三角形的一个底角的度数为25°或65°.
故填25°或65°.
【点评】本题考查了等腰三角形的性质及三角形内角和定理;等腰三角形的高线,可能在三角形的内部,边上、外部几种不同情况,因而,遇到与等腰三角形的高有关的计算时应分类讨论.
【考点】一元一次不等式组的整数解
【分析】解不等式组得出其解集为﹣2<x≤,根据不等式组有且只有三个整数解得出1≤<2,解之可得答案.
解:解不等式,得:x>﹣2,
解不等式2x﹣m≤2﹣x,得:x≤,
则不等式组的解集为﹣2<x≤,
∵不等式组有且只有三个整数解,
∴1≤<2,
解得:1≤m<4,
故答案为:1≤m<4.
【点评】本题考查了不等式组的整数解,关键是根据不等式组的整数解求出取值范围,用到的知识点是一元一次不等式的解法.
1 、解答题
【考点】分式的化简求值.
【分析】原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解:原式=
=
=x+1,
当x=3﹣3时,原式=3﹣3+1=3﹣2.
【点评】此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.
【考点】解一元一次不等式;实数的运算;零指数幂.
【分析】(1)原式利用零指数幂法则,绝对值的代数意义,以及二次根式性质计算即可得到结果;
(2)去括号,移项,合并同类项,系数化成1即可求出不等式的解集.
解:(1)原式=1
=﹣3;
(2)去括号,得4x+5≤2x+2
移项合并同类项得,2x≤﹣3
解得x.
【点评】此题考查了实数的运算和一元一次不等式的运算,零指数幂、负整数指数幂,熟练拿握运算法则是解本题的关键。
【考点】二次根式的混合运算,求一个数的立方根
【分析】(1)①从左往右依次计算开平方、乘方、开立方、约分,再计算加减即可;
②先去括号和绝对值,再计算加减即可;
(2)①根据绝对值的性质直接去绝对值即可;
②利用立方根的性质计算即可.
解:(1)①原式
②原式
(2)①
②
【点评】本题考查了二次根式的混合运算、求绝对值、求一个数的立方根,熟练掌握运算法则是解题的关键.
【考点】一元一次不等式组的应用
【分析】已知该同学的家到学校共需支付车费24.8元,从同学的家到学校的距离为x千米,首先去掉前2千米的费用,从而根据题意列出不等式,从而得出答案.
解:设该同学的家到学校的距离是x千米,依题意:
13.8﹣1.8<5+1.8(x﹣2)≤24.8,
解得:12<x≤13.
故该同学的家到学校的距离在大于12小于等于13的范围.
【点评】此题主要考查了一元一次不等式的应用,根据题意明确其收费标准分两部分是完成本题的关键.
【考点】线段垂直平分线的性质
【分析】根据线段垂直平分线的性质得到CA=CE,AB=AC,根据三角形的周长公式计算,得到答案.
解:∵点C在AE的垂直平分线上,
∴CA=CE,
∵AD⊥BE,BD=DC,
∴AB=AC,
∵△ABC的周长为18,
∴AB+BC+AC=18,
∴2AC+2DC=18,
∴AC+DC=9,
∴DE=DC+CE=AC+CD=9(cm).
【点评】本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
【考点】分式方程的应用;二元一次方程的应用.
【分析】(1)首先设这种笔单价为x元,则本子单价为(x﹣4)元,根据题意可得等量关系:30元买这种本子的数量=50元买这种笔的数量,由等量关系可得方程=,再解方程可得答案;
(2)设恰好用完100元,可购买这种笔m支和购买本子n本,根据题意可得这种笔的单价×这种笔的支数m+本子的单价×本子的本数n=1000,再求出整数解即可.
解:(1)设这种笔单价为x元,则本子单价为(x﹣4)元,由题意得:
=,
解得:x=10,
经检验:x=10是原分式方程的解,
则x﹣4=6.
答:这种笔单价为10元,则本子单价为6元;
(2)设恰好用完100元,可购买这种笔m支和购买本子n本,
由题意得:10m+6n=100,
整理得:m=10﹣n,
∵m、n都是正整数,
∴①n=5时,m=7,②n=10时,m=4,③n=15,m=1;
∴有三种方案:
①购买这种笔7支,购买本子5本;
②购买这种笔4支,购买本子10本;
③购买这种笔1支,购买本子15本.
【点评】此题主要考查了分式方程和二元一次方程的应用,关键是正确理解题意,找出题目中的等量关系,列出方程.
【考点】轴对称-最短路线问题;线段垂直平分线的性质;等腰三角形的性质.
【分析】(1)根据等腰三角的性质,三角形的内角和定理,可得∠A的度数,根据直角三角形两锐角的关系,可得答案;
(2)根据等腰三角的性质,三角形的内角和定理,可得∠A的度数,根据直角三角形两锐角的关系,可得答案;
(3)根据垂直平分线的性质,可得AM与MB的关系,再根据三角形的周长,可得答案;根据两点之间线段最短,可得P点与M点的关系,可得PB+PC与AC的关系.
解:(1)若∠B=70°,则∠NMA的度数是 50°,
故答案为:50°;
(2)猜想的结论为:∠NMA=2∠B﹣90°.
理由:∵AB=AC,
∴∠B=∠C,
∴∠A=180°﹣2∠B,
又∵MN垂直平分AB,
∴∠NMA=90°﹣∠A=90°﹣(180°﹣2∠B)=2∠B﹣90°.
(3)如图:
①∵MN垂直平分AB.
∴MB=MA,
又∵△MBC的周长是14cm,
∴AC+BC=14cm,
∴BC=6cm.
②当点P与点M重合时,PB+CP的值最小,最小值是8cm.
【点评】本题考查了轴对称,线段垂直平分线上的点到线段两端点的距离相等得出PB=PA.
【考点】全等三角形的判定好性质,多边形内角和,直角三角形的性质
【分析】根据四边形的内角和定理得出DE⊥AB,从而得到BE的长度;取AB的中点G,连接DG,得出DG为△ABC的中位线,则DG=DC,∠BGD=∠C=60°,根据四边形对角互补得出∠GED=∠DFC,从而得到△DEG和△DFC全等,得到EG=CF,得出答案;取AB的中点G,连接DG,同⑵,易证△DEG≌△DFC得出EG=CF,设CN=x,根据Rt△DCN得出CD=2x,DN=x,根据题意得出EG、BE与x的关系,从而进行说明.
解:⑴由四边形AEDF的内角和为360°,可知DE⊥AB,故BE=2
⑵取AB的中点G,连接DG
易证:DG为△ABC的中位线,故DG=DC,∠BGD=∠C=60°
又四边形AEDF的对角互补,故∠GED=∠DFC
∴△DEG≌△DFC
故EG=CF
∴BE+CF=BE+EG=BG=AB
⑶取AB的中点G,连接DG
同⑵,易证△DEG≌△DFC
故EG=CF
故BE-CF=BE-EG=BG=AB
设CN=x
在Rt△DCN中,CD=2x,DN=x
在RT△DFN中,NF=DN=x,故EG=CF=(-1)x
BE=BG+EG=DC+CF=2x+(-1)x =(+1)x
故BE+CF=(+1)x+(-1)x=2x,
(BE-CF)=[(+1) x-(-1)x]= 2x.
故.
【点评】本题主要考查了等边三角形的判定与性质、四边形的内角和定理、全等三角形的判定与性质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
