2021-2022学年人教版九年级数学下册 28.2解直角三角形及其应用 填空题专题训练 (word版含解析)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册 28.2解直角三角形及其应用 填空题专题训练 (word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 624.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览


文档简介
2021-2022学年人教版九年级数学下册《28.2解直角三角形及其应用》
填空题专题训练(附答案)
1.如图,一艘轮船位于灯塔P的南偏东60°方向,距离灯塔50海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东45°方向上的B处,此时B处与灯塔P的距离为 海里(结果保留根号).
2.如图,海中有一个小岛A.一艘轮船由西向东航行,在B点测得小岛A在北偏东60°方向上;航行12nmile到达C点,这时测得小岛A在北偏东30°方向上.小岛A到航线BC的距离是 nmile(≈1.73,结果用四舍五入法精确到0.1).
3.如图,某海防哨所O发现在它的西北方向,距离哨所400米的A处有一艘船向正东方向航行,航行一段时间后到达哨所北偏东60°方向的B处,则此时这艘船与哨所的距离OB约为 米.(精确到1米,参考数据:≈1.414,≈1.732)
4.如图,一艘渔船正以60海里/小时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1.5小时后到达B处,此时测得岛礁P在北偏东30°方向,同时测得岛礁P正东方向上的避风港M在北偏东60°方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/小时的速度继续航行 小时即可到达.(结果保留根号)
5.在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度为 米.(结果保留根号)
6.如图,为了测量河宽AB(假设河的两岸平行),测得∠ACB=30°,∠ADB=60°,CD=60m,则河宽AB为 m(结果保留根号).
7.如图,海平面上灯塔O方圆100千米范围内有暗礁.一艘轮船自西向东方向航行,在点A处测量得灯塔O在北偏东60°方向,继续航行100千米后,在点B处测量得灯塔O在北偏东37°方向.请你作出判断,为了避免触礁,这艘轮船是否要改变航向? .(填“是”或“否”,参考数据:sin37°≈0.6018,cos37°≈0.7986,tan37°≈0.7536,cot37°≈1.327,≈1.732).
8.如图,A市东偏北60°方向有一旅游景点M,在A市东偏北30°的公路上向前行800米到C处,测得M位于C的北偏西15°,则景点M到公路AC的距离MN为 米(结果保留根号).
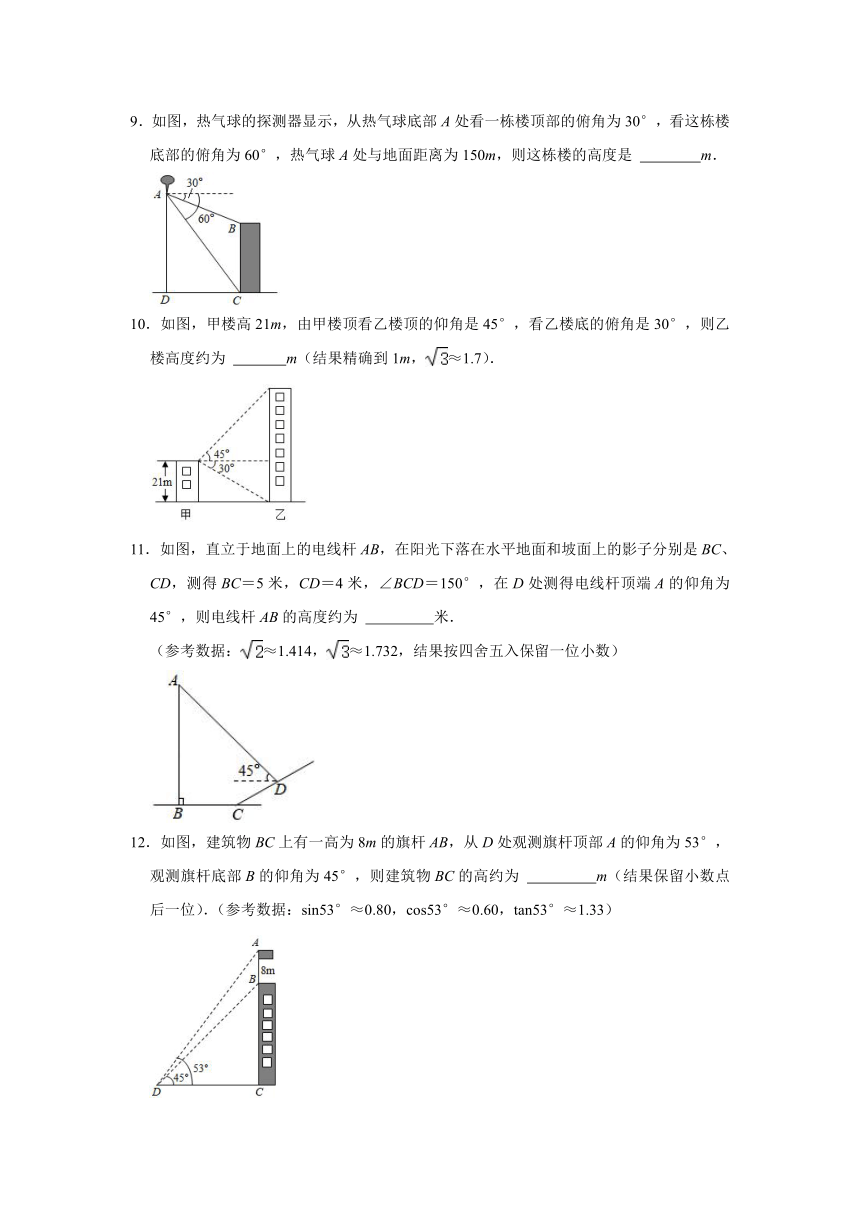
9.如图,热气球的探测器显示,从热气球底部A处看一栋楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处与地面距离为150m,则这栋楼的高度是 m.
10.如图,甲楼高21m,由甲楼顶看乙楼顶的仰角是45°,看乙楼底的俯角是30°,则乙楼高度约为 m(结果精确到1m,≈1.7).
11.如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=5米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为45°,则电线杆AB的高度约为 米.
(参考数据:≈1.414,≈1.732,结果按四舍五入保留一位小数)
12.如图,建筑物BC上有一高为8m的旗杆AB,从D处观测旗杆顶部A的仰角为53°,观测旗杆底部B的仰角为45°,则建筑物BC的高约为 m(结果保留小数点后一位).(参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
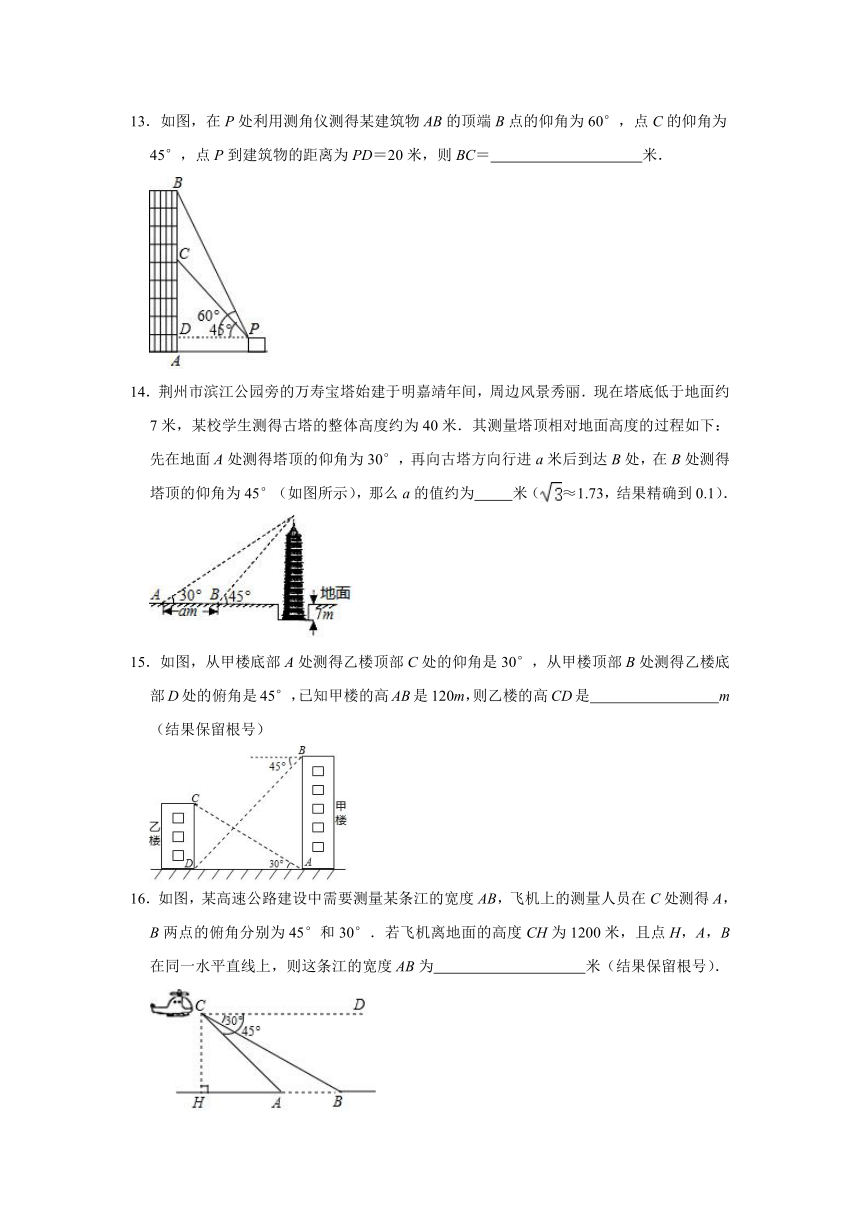
13.如图,在P处利用测角仪测得某建筑物AB的顶端B点的仰角为60°,点C的仰角为45°,点P到建筑物的距离为PD=20米,则BC= 米.
14.荆州市滨江公园旁的万寿宝塔始建于明嘉靖年间,周边风景秀丽.现在塔底低于地面约7米,某校学生测得古塔的整体高度约为40米.其测量塔顶相对地面高度的过程如下:先在地面A处测得塔顶的仰角为30°,再向古塔方向行进a米后到达B处,在B处测得塔顶的仰角为45°(如图所示),那么a的值约为 米(≈1.73,结果精确到0.1).
15.如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知甲楼的高AB是120m,则乙楼的高CD是 m(结果保留根号)
16.如图,某高速公路建设中需要测量某条江的宽度AB,飞机上的测量人员在C处测得A,B两点的俯角分别为45°和30°.若飞机离地面的高度CH为1200米,且点H,A,B在同一水平直线上,则这条江的宽度AB为 米(结果保留根号).
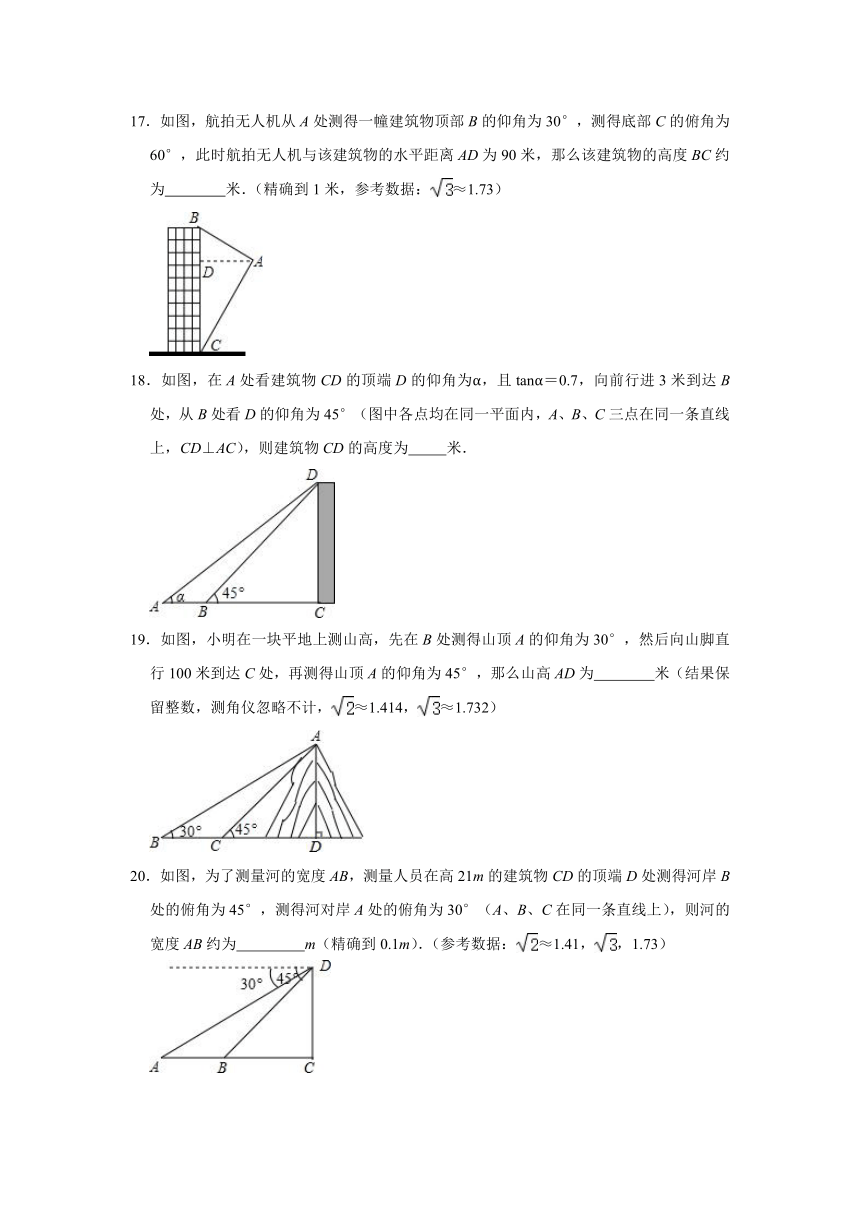
17.如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为90米,那么该建筑物的高度BC约为 米.(精确到1米,参考数据:≈1.73)
18.如图,在A处看建筑物CD的顶端D的仰角为α,且tanα=0.7,向前行进3米到达B处,从B处看D的仰角为45°(图中各点均在同一平面内,A、B、C三点在同一条直线上,CD⊥AC),则建筑物CD的高度为 米.
19.如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为 米(结果保留整数,测角仪忽略不计,≈1.414,≈1.732)
20.如图,为了测量河的宽度AB,测量人员在高21m的建筑物CD的顶端D处测得河岸B处的俯角为45°,测得河对岸A处的俯角为30°(A、B、C在同一条直线上),则河的宽度AB约为 m(精确到0.1m).(参考数据:≈1.41,,1.73)
21.如图,某校教学楼后面紧邻着一个山坡,坡上面是一块平地.BC∥AD,BE⊥AD,斜坡AB长26m,斜坡AB的坡比为12:5.为了减缓坡面,防止山体滑坡,学校决定对该斜坡进行改造.经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.如果改造时保持坡脚A不动,则坡顶B沿BC至少向右移 m时,才能确保山体不滑坡.(取tan50°≈1.2)
22.如图,一架长为6米的梯子AB斜靠在一竖直的墙AO上,这时测得∠ABO=70°,如果梯子的底端B外移到D,则梯子顶端A下移到C,这时又测得∠CDO=50°,那么AC的长度约为 米.(sin70°≈0.94,sin50°≈0.77,cos70°≈0.34,cos50°≈0.64)
23.为加强防汛工作,某市对一拦水坝进行加固.如图,加固前拦水坝的横断面是梯形ABCD.已知迎水坡面AB=12米,背水坡面CD=12米,∠B=60°,加固后拦水坝的横断面为梯形ABED,tanE=,则CE的长为 米.
24.如图是市民广场到解百地下通道的手扶电梯示意图.其中AB、CD分别表示地下通道、市民广场电梯口处地面的水平线,∠ABC=135°,BC的长约是m,则乘电梯从点B到点C上升的高度h是 m.
25.长为4m的梯子搭在墙上与地面成45°角,作业时调整为60°角(如图所示),则梯子的顶端沿墙面升高了 m.
26.“健康荆州,你我同行”,市民小张积极响应“全民健身动起来”号召,坚持在某环形步道上跑步.已知此步道外形近似于如图所示的Rt△ABC,其中∠C=90°,AB与BC间另有步道DE相连,D地在AB正中位置,E地与C地相距1km.若tan∠ABC=,∠DEB=45°,小张某天沿A→C→E→B→D→A路线跑一圈,则他跑了 km.
27.如图是矗立在高速公路边水平地面上的交通警示牌,经过测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则CD的长为 米.(结果保留根号)
28.如图是引拉线固定电线杆的示意图.已知:CD⊥AB,CD=m,∠CAD=∠CBD=60°,则拉线AC的长是 m.
29.如图,一束光线从y轴上点A(0,1)出发,经过x轴上点C反射后经过点B(3,3),则光线从A点到B点经过的路线长是 .
30.如图,△ABC的顶点B、C的坐标分别是(1,0)、(0,),且∠ABC=90°,∠A=30°,则顶点A的坐标是 .
31.如图,已知点A(4,3),点B为直线y=﹣2上的一动点,点C(0,n),﹣2<n<3,AC⊥BC于点C,连接AB.若直线AB与x轴正半轴所夹的锐角为α,那么当sinα的值最大时,n的值为 .
32.如图,在由10个完全相同的正三角形构成的网格图中,∠α、∠β如图所示,则cos(α+β)= .
33.如图,在Rt△ABC中,∠C=90°,点D是AB的中点,ED⊥AB交AC于点E.设∠A=α,且tanα=,则tan2α= .
34.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E,BC=6,sinA=,则DE= .
35.将一副三角尺如图所示叠放在一起,若AB=14cm,则阴影部分的面积是 cm2.
36.芜湖国际动漫节期间,小明进行了富有创意的形象设计.如图1,他在边长为1的正方形ABCD内作等边三角形BCE,并与正方形的对角线交于F、G点,制成如图2的图标.则图标中阴影部分图形AFEGD的面积= .
参考答案
1.解:过P作PC⊥AB于C,如图所示:
由题意得:∠APC=30°,∠BPC=45°,PA=50海里,
在Rt△APC中,cos∠APC=,
∴PC=PA cos∠APC=50×=25(海里),
在Rt△PCB中,cos∠BPC=,
∴PB===25(海里),
故答案为:25.
2.解:过点A作AE⊥BC交BC的延长线于点E,
由题意得,∠BAE=60°,∠CAE=30°,
∴∠ABC=30°,∠ACE=60°,
∴∠BAC=∠ACE﹣∠ABC=30°,
∴∠BAC=∠ABC,
∴AC=BC=12nmile,
在Rt△ACE中,sin∠ACE=,
∴AE=AC sin∠ACE=6≈10.4(nmile),
故小岛A到航线BC的距离是10.4nmile,
故答案为10.4.
3.解:如图,设线段AB交y轴于C,
在直角△OAC中,∠COA=∠CAO=45°,则AC=OC.
∵OA=400米,
∴OC=OA cos45°=400×=200(米).
∵在直角△OBC中,∠COB=60°,OC=200米,
∴OB===400≈566(米)
故答案是:566.
4.解:如图,过点P作PQ⊥AB交AB延长线于点Q,过点M作MN⊥AB交AB延长线于点N,
在直角△AQP中,∠PAQ=45°,则AQ=PQ=60×1.5+BQ=90+BQ(海里),
所以 BQ=PQ﹣90.
在直角△BPQ中,∠BPQ=30°,则BQ=PQ tan30°=PQ(海里),
所以 PQ﹣90=PQ,
所以 PQ=45(3+)(海里)
所以 MN=PQ=45(3+)(海里)
在直角△BMN中,∠MBN=30°,
所以 BM=2MN=90(3+)(海里)
所以 =(小时)
故答案是:.
5.解:如图作BH⊥EF,CK⊥MN,垂足分别为H、K,则四边形BHCK是矩形,
设CK=HB=x,
∵∠CKA=90°,∠CAK=45°,
∴∠CAK=∠ACK=45°,
∴AK=CK=x,BK=HC=AK﹣AB=x﹣30,
∴HD=x﹣30+10=x﹣20,
在RT△BHD中,∵∠BHD=90°,∠HBD=30°,
∴tan30°=,
∴=,
解得x=30+10.
∴河的宽度为(30+10)米.
6.解:∵∠ACB=30°,∠ADB=60°,
∴∠CAD=30°,
∴AD=CD=60m,
在Rt△ABD中,
AB=AD sin∠ADB=60×=30(m).
故答案为:30.
7.解:过点O作OC垂直于AB的延长线于点C.
在Rt△COB中,∠BOC=37°,BC=OCtan37°,
在Rt△AOC中,∠AOC=60°,AC=OCtan60°=OC,
又∵AC=AB+BC,AB=100(km),
即OC=100+OC tan37°,
∴OC=≈102.2(千米).
故OC>100千米,这艘轮船可以不改变航向,不会触礁.
8.解:过点C作CP⊥AM.
∵AC=800米,∠MAC=30°,∠ACM=180°﹣(90°﹣30°+15°)=105°,
∴∠AMC=45°,
∴CP=PM=400米,AP=400米,
∴AM=400+400米,
∵AM PC=AC MN,
∴MN=200+200(米).
9.解:如图,过A作AH⊥BC,交CB的延长线于点H,
在Rt△ACD中,
∵∠CAD=30°,AD=150m,
∴CD=AD tan30°=150×=50(m),
∴AH=CD=50m.
在Rt△ABH中,
∵∠BAH=30°,AE=50m,
∴BH=AH tan30°=50×=50(m),
∴BC=AD﹣BH=150﹣50=100(m),
答:这栋楼的高度为100m.
故答案为:100.
10.解:如图,过A作AE⊥CD于E,
则AB=CE,
在△ACE中,∵∠AEC=90°,∠CAE=30°,EC=AB=21米,
∴AC=21×2=42(米),
∴AE===21≈35.7(米),
在Rt△ADE中,∵∠AED=90°,∠DAE=45°,
∴AE=DE=35.7米,
∴乙楼DC=CE+ED=21+35.7=56.7≈57(米).
答:乙楼的高约为57米.
11.解:延长AD交BC的延长线于E,作DF⊥BE于F,
∵∠BCD=150°,
∴∠DCF=30°,又CD=4米,
∴DF=2米,CF=(米),
由题意得∠E=45°,
∴EF=DF=2米,
∴BE=BC+CF+EF=5+2+2=(7+2)米,
∴AB=BE=7+2≈10.5(米),
故答案为10.5.
12.解:在Rt△BCD中,∠BDC=45°,
则BC=CD,
设BC=CD=x,则AC=x+8,
在Rt△ACD中,tan∠ADC==,
则x+8=x tan53°,
∴x+8=1.33x,
∴x≈24.2(m),
故建筑物BC的高约为24.2m,
故答案为:24.2.
13.解:在Rt△PBD中,tan∠BPD=,
则BD=PD tan∠BPD=20(米),
在Rt△PBD中,∠CPD=45°,
∴CD=PD=20(米),
∴BC=BD﹣CD=(20﹣20)米,
故答案为:(20﹣20).
14.解:如图,设CD为塔身的高,延长AB交CD于E,则CD=40,DE=7,
∴CE=33,
∵∠CBE=45°=∠BCE,∠CAE=30°,
∴BE=CE=33,
∴AE=a+33,
∵tanA=,
∴tan30°=,即33=a+33,
解得a=33(﹣1)≈24.1,
∴a的值约为24.1米,
故答案为:24.1.
15.解:由题意可得:∠BDA=45°,
则AB=AD=120m,
又∵∠CAD=30°,
∴在Rt△ADC中,
tan∠CAD=tan30°==,
解得:CD=40(m),
故答案为:40.
16.解:由于CD∥HB,
∴∠CAH=∠ACD=45°,∠B=∠BCD=30°
在Rt△ACH中,∵∴∠CAH=45°
∴AH=CH=1200米,
在Rt△HCB,∵tan∠B=
∴HB==
==1200(米).
∴AB=HB﹣HA
=1200﹣1200
=1200(﹣1)米
故答案为:1200(﹣1)
17.解:由题意可得:tan30°===,
解得:BD=30(m),
tan60°===,
解得:DC=90(m),
故该建筑物的高度为:BC=BD+DC=120≈208(m),
故答案为:208.
18.解:∵∠DBC=45°,
∴BC=CD,
tanα==,
则=,
解得CD=7(米).
故答案为:7.
19.解:如图,∠ABD=30°,∠ACD=45°,BC=100m,
设AD=xm,
在Rt△ACD中,∵tan∠ACD=,
∴CD=AD=x,
∴BD=BC+CD=x+100,
在Rt△ABD中,∵tan∠ABD=,
∴x=(x+100),
∴x=50(+1)≈137,
即山高AD为137米.
故答案为137.
20.解:在Rt△ACD中,CD=21m,∠DAC=30°,
则AC=CD≈36.3m;
在Rt△BCD中,∠DBC=45°,
则BC=CD=21m,
故AB=AC﹣BC=15.3m.
故答案为:15.3.
21.解:在BC上取点F,使∠FAE=50°,过点F作FH⊥AD于H,
∵BF∥EH,BE⊥AD,FH⊥AD,
∴四边形BEHF为矩形,
∴BF=EH,BE=FH,
∵斜坡AB的坡比为12:5,
∴=,
设BE=12xm,则AE=5xm,
由勾股定理得,AE2+BE2=AB2,即(5x)2+(12x)2=262,
解得,x=2,
∴AE=10m,BE=24m,
∴FH=BE=24m,
在Rt△FAH中,tan∠FAH=,
∴AH=≈20(m),
∴BF=EH=AH﹣AE=10(m),
∴坡顶B沿BC至少向右移10m时,才能确保山体不滑坡,
故答案为:10.
22.解:由题意可得:
∵∠ABO=70°,AB=6m,
∴sin70°==≈0.94,
解得:AO=5.64(m),
∵∠CDO=50°,DC=6m,
∴sin50°=≈0.77,
解得:CO=4.62(m),
则AC=5.64﹣4.62=1.02(m),
答:AC的长度约为1.02米.
故答案为:1.02.
23.解:分别过A、D作AF⊥BC,DG⊥BC,垂点分别为F、G,如图所示.
∵在Rt△ABF中,AB=12米,∠B=60°,
∴sin∠B=,
∴AF=12×=6(米),
∴DG=6(米).
∵在Rt△DGC中,CD=12米,DG=6米,
∴GC==18米.
∵在Rt△DEG中,tanE=,
∴=,
∴GE=26米,
∴CE=GE﹣CG=26﹣18=8(米).
即CE的长为8米.
故答案为8.
24.解:过点C作AB的延长线的垂线CE,即乘电梯从点B到点C上升的高度h,
已知∠ABC=135°,
∴∠CBE=180°﹣∠ABC=45°,
∴CE=BC sin∠CBE=5 sin45°=5 =5.
所以h=5,
故答案为:5.
25.解:由题意知:平滑前梯高为4 sin45°=4 =.
平滑后高为4 sin60°=4 =.
∴升高了2()m.
故答案为:2().
26.解:过D点作DF⊥BC,
设EF=xkm,则DF=xkm,BF=xkm,
在Rt△BFD中,BD==xkm,
∵D地在AB正中位置,
∴AB=2BD=xkm,
∵tan∠ABC=,
∴cos∠ABC=,
∴=,
解得x=3,
则BC=8km,AC=6km,AB=10km,
小张某天沿A→C→E→B→D→A路线跑一圈,他跑了8+10+6=24(km).
故答案为:24.
27.解:在Rt△CMB中,∵∠CMB=90°,MB=AM+AB=12米,∠MBC=30°,
∴CM=MB tan30°=12×=4,
在Rt△ADM中,∵∠AMD=90°,∠MAD=45°,
∴∠MAD=∠MDA=45°,
∴MD=AM=4米,
∴CD=CM﹣DM=(4﹣4)米,
故答案为:4﹣4.
28.解:AC=CD÷sin60°=6(米).
29.解:A关于x轴的对称点A′坐标是(0,﹣1)连接A′B,交x轴于点C,
作DB∥A′A,A′D∥OC,交DB于D,
故光线从点A到点B所经过的路程A′B===5.
30.解:过点A作AG⊥x轴,交x轴于点G.
∵B、C的坐标分别是(1,0)、(0,),
∴OC=,OB=1,
∴BC==2.
∵∠ABC=90°,∠BAC=30°,
∴AB====2.
∵∠ABG+∠CBO=90°,∠BCO+∠CBO=90°,
∴∠ABG=∠BCO.
∴sin∠ABG===,cos∠ABG===,
∴AG=,BG=3.
∴OG=1+3=4,
∴顶点A的坐标是(4,).
故答案为:(4,).
31.解:过点A作AM⊥y轴于点M,作AN⊥BN交于点N,
∵直线y=﹣2∥x轴,故∠ABN=α,
当sinα的值最大时,则tanα=值最大,
故BN最小,即BG最大时,tanα最大,
即当BG最大时,sinα的值最大,
设BG=y,
则AM=4,GC=n+2,CM=3﹣n,
∵∠ACM+∠MAC=90°,∠ACM+∠BCG=90°,
∴∠CAM=∠BCG,
∴tan∠CAM=tan∠BCG,
∴,即,
∴y=﹣(n﹣3)(n+2),
∵﹣<0,
故当n=(3﹣2)=时,y取得最大值,
故n=,
故答案为:.
32.解:给图中相关点标上字母,连接DE,如图所示.
在△ABC中,∠ABC=120°,BA=BC,
∴∠α=30°.
同理,可得出:∠CDE=∠CED=30°=∠α.
又∵∠AEC=60°,
∴∠AED=∠AEC+∠CED=90°.
设等边三角形的边长为a,则AE=2a,DE=2×sin60° a=a,
∴AD==a,
∴cos(α+β)==.
故答案为:.
33.解:连接BE,
∵点D是AB的中点,ED⊥AB,∠A=α,
∴ED是AB的垂直平分线,
∴EB=EA,
∴∠EBA=∠A=α,
∴∠BEC=2α,
∵tanα=,设DE=a,
∴AD=3a,AE=,
∴AB=6a,
∴BC=,AC=
∴CE=AC﹣AE=,
∴tan2α=,
故答案为:.
34.解:∵BC=6,sinA=,
∴AB=10,
∴AC==8,
∵D是AB的中点,
∴AD=AB=5,
∵△ADE∽△ACB,
∴=,即=,
解得:DE=.
故答案为:.
35.解:∵∠B=30°,∠ACB=90°,AB=14cm,
∴AC=7cm.
由题意可知BC∥ED,
∴∠AFC=∠ADE=45°,
∴AC=CF=7cm.
故S△ACF=×7×7=(cm2).
故答案为:.
36.解:方法1:设AC与BD交于点O,
∵AC、BD是正方形的对角线,
∴AC⊥BD,OA=OB,
在△BCE中,∠EBC=60°,∠OBC=45°,
∴∠EBO=60°﹣45°,
∴FO=tan(60°﹣45°) OB,
∴S△BOF=OF OB=tan(60°﹣45°) OB2,
∴S△BAF=S△BAO﹣S△BOF=﹣tan(60°﹣45°) OB2=﹣tan(60°﹣45°) OB2=OB2,
同理,得S△CGD=OB2,
∵S△CBE=sin60°=sin60°=AB2,
∴S ABCD﹣S△CBE﹣S△BAF﹣S△CGD=AB2﹣AB2﹣OB2,
∵OB=BD,BD2=AB2+AD2,AB=AD=1,
∴S ABCD﹣S△CBE﹣S△BAF﹣S△CGD=1﹣﹣(××(1+1)=,
图标中阴影部分图形AFEGD的面积=.
方法2:过G作GH⊥CD于H,
则易得△GDH是等腰直角三角形,设DH=GH=x,
∵△BEC是等边三角形,
∴∠BCE=60°,
∴∠ECD=90°﹣60°=30°,
∴CH=GH÷tan30°=x÷=x,
∵CD=DH+CH=1,
即x+x=1,
x(1+)=1,
解得x===,
∴S△CGD=×1×=
同理S△BFA=
易得S△BCE=
∴S阴影=S正方形ABCD﹣S△BCE﹣S△BAF﹣S△CGD
=1﹣﹣﹣
=.
故答案为:.
填空题专题训练(附答案)
1.如图,一艘轮船位于灯塔P的南偏东60°方向,距离灯塔50海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东45°方向上的B处,此时B处与灯塔P的距离为 海里(结果保留根号).
2.如图,海中有一个小岛A.一艘轮船由西向东航行,在B点测得小岛A在北偏东60°方向上;航行12nmile到达C点,这时测得小岛A在北偏东30°方向上.小岛A到航线BC的距离是 nmile(≈1.73,结果用四舍五入法精确到0.1).
3.如图,某海防哨所O发现在它的西北方向,距离哨所400米的A处有一艘船向正东方向航行,航行一段时间后到达哨所北偏东60°方向的B处,则此时这艘船与哨所的距离OB约为 米.(精确到1米,参考数据:≈1.414,≈1.732)
4.如图,一艘渔船正以60海里/小时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1.5小时后到达B处,此时测得岛礁P在北偏东30°方向,同时测得岛礁P正东方向上的避风港M在北偏东60°方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/小时的速度继续航行 小时即可到达.(结果保留根号)
5.在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度为 米.(结果保留根号)
6.如图,为了测量河宽AB(假设河的两岸平行),测得∠ACB=30°,∠ADB=60°,CD=60m,则河宽AB为 m(结果保留根号).
7.如图,海平面上灯塔O方圆100千米范围内有暗礁.一艘轮船自西向东方向航行,在点A处测量得灯塔O在北偏东60°方向,继续航行100千米后,在点B处测量得灯塔O在北偏东37°方向.请你作出判断,为了避免触礁,这艘轮船是否要改变航向? .(填“是”或“否”,参考数据:sin37°≈0.6018,cos37°≈0.7986,tan37°≈0.7536,cot37°≈1.327,≈1.732).
8.如图,A市东偏北60°方向有一旅游景点M,在A市东偏北30°的公路上向前行800米到C处,测得M位于C的北偏西15°,则景点M到公路AC的距离MN为 米(结果保留根号).
9.如图,热气球的探测器显示,从热气球底部A处看一栋楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处与地面距离为150m,则这栋楼的高度是 m.
10.如图,甲楼高21m,由甲楼顶看乙楼顶的仰角是45°,看乙楼底的俯角是30°,则乙楼高度约为 m(结果精确到1m,≈1.7).
11.如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=5米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为45°,则电线杆AB的高度约为 米.
(参考数据:≈1.414,≈1.732,结果按四舍五入保留一位小数)
12.如图,建筑物BC上有一高为8m的旗杆AB,从D处观测旗杆顶部A的仰角为53°,观测旗杆底部B的仰角为45°,则建筑物BC的高约为 m(结果保留小数点后一位).(参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
13.如图,在P处利用测角仪测得某建筑物AB的顶端B点的仰角为60°,点C的仰角为45°,点P到建筑物的距离为PD=20米,则BC= 米.
14.荆州市滨江公园旁的万寿宝塔始建于明嘉靖年间,周边风景秀丽.现在塔底低于地面约7米,某校学生测得古塔的整体高度约为40米.其测量塔顶相对地面高度的过程如下:先在地面A处测得塔顶的仰角为30°,再向古塔方向行进a米后到达B处,在B处测得塔顶的仰角为45°(如图所示),那么a的值约为 米(≈1.73,结果精确到0.1).
15.如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知甲楼的高AB是120m,则乙楼的高CD是 m(结果保留根号)
16.如图,某高速公路建设中需要测量某条江的宽度AB,飞机上的测量人员在C处测得A,B两点的俯角分别为45°和30°.若飞机离地面的高度CH为1200米,且点H,A,B在同一水平直线上,则这条江的宽度AB为 米(结果保留根号).
17.如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为90米,那么该建筑物的高度BC约为 米.(精确到1米,参考数据:≈1.73)
18.如图,在A处看建筑物CD的顶端D的仰角为α,且tanα=0.7,向前行进3米到达B处,从B处看D的仰角为45°(图中各点均在同一平面内,A、B、C三点在同一条直线上,CD⊥AC),则建筑物CD的高度为 米.
19.如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为 米(结果保留整数,测角仪忽略不计,≈1.414,≈1.732)
20.如图,为了测量河的宽度AB,测量人员在高21m的建筑物CD的顶端D处测得河岸B处的俯角为45°,测得河对岸A处的俯角为30°(A、B、C在同一条直线上),则河的宽度AB约为 m(精确到0.1m).(参考数据:≈1.41,,1.73)
21.如图,某校教学楼后面紧邻着一个山坡,坡上面是一块平地.BC∥AD,BE⊥AD,斜坡AB长26m,斜坡AB的坡比为12:5.为了减缓坡面,防止山体滑坡,学校决定对该斜坡进行改造.经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.如果改造时保持坡脚A不动,则坡顶B沿BC至少向右移 m时,才能确保山体不滑坡.(取tan50°≈1.2)
22.如图,一架长为6米的梯子AB斜靠在一竖直的墙AO上,这时测得∠ABO=70°,如果梯子的底端B外移到D,则梯子顶端A下移到C,这时又测得∠CDO=50°,那么AC的长度约为 米.(sin70°≈0.94,sin50°≈0.77,cos70°≈0.34,cos50°≈0.64)
23.为加强防汛工作,某市对一拦水坝进行加固.如图,加固前拦水坝的横断面是梯形ABCD.已知迎水坡面AB=12米,背水坡面CD=12米,∠B=60°,加固后拦水坝的横断面为梯形ABED,tanE=,则CE的长为 米.
24.如图是市民广场到解百地下通道的手扶电梯示意图.其中AB、CD分别表示地下通道、市民广场电梯口处地面的水平线,∠ABC=135°,BC的长约是m,则乘电梯从点B到点C上升的高度h是 m.
25.长为4m的梯子搭在墙上与地面成45°角,作业时调整为60°角(如图所示),则梯子的顶端沿墙面升高了 m.
26.“健康荆州,你我同行”,市民小张积极响应“全民健身动起来”号召,坚持在某环形步道上跑步.已知此步道外形近似于如图所示的Rt△ABC,其中∠C=90°,AB与BC间另有步道DE相连,D地在AB正中位置,E地与C地相距1km.若tan∠ABC=,∠DEB=45°,小张某天沿A→C→E→B→D→A路线跑一圈,则他跑了 km.
27.如图是矗立在高速公路边水平地面上的交通警示牌,经过测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则CD的长为 米.(结果保留根号)
28.如图是引拉线固定电线杆的示意图.已知:CD⊥AB,CD=m,∠CAD=∠CBD=60°,则拉线AC的长是 m.
29.如图,一束光线从y轴上点A(0,1)出发,经过x轴上点C反射后经过点B(3,3),则光线从A点到B点经过的路线长是 .
30.如图,△ABC的顶点B、C的坐标分别是(1,0)、(0,),且∠ABC=90°,∠A=30°,则顶点A的坐标是 .
31.如图,已知点A(4,3),点B为直线y=﹣2上的一动点,点C(0,n),﹣2<n<3,AC⊥BC于点C,连接AB.若直线AB与x轴正半轴所夹的锐角为α,那么当sinα的值最大时,n的值为 .
32.如图,在由10个完全相同的正三角形构成的网格图中,∠α、∠β如图所示,则cos(α+β)= .
33.如图,在Rt△ABC中,∠C=90°,点D是AB的中点,ED⊥AB交AC于点E.设∠A=α,且tanα=,则tan2α= .
34.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E,BC=6,sinA=,则DE= .
35.将一副三角尺如图所示叠放在一起,若AB=14cm,则阴影部分的面积是 cm2.
36.芜湖国际动漫节期间,小明进行了富有创意的形象设计.如图1,他在边长为1的正方形ABCD内作等边三角形BCE,并与正方形的对角线交于F、G点,制成如图2的图标.则图标中阴影部分图形AFEGD的面积= .
参考答案
1.解:过P作PC⊥AB于C,如图所示:
由题意得:∠APC=30°,∠BPC=45°,PA=50海里,
在Rt△APC中,cos∠APC=,
∴PC=PA cos∠APC=50×=25(海里),
在Rt△PCB中,cos∠BPC=,
∴PB===25(海里),
故答案为:25.
2.解:过点A作AE⊥BC交BC的延长线于点E,
由题意得,∠BAE=60°,∠CAE=30°,
∴∠ABC=30°,∠ACE=60°,
∴∠BAC=∠ACE﹣∠ABC=30°,
∴∠BAC=∠ABC,
∴AC=BC=12nmile,
在Rt△ACE中,sin∠ACE=,
∴AE=AC sin∠ACE=6≈10.4(nmile),
故小岛A到航线BC的距离是10.4nmile,
故答案为10.4.
3.解:如图,设线段AB交y轴于C,
在直角△OAC中,∠COA=∠CAO=45°,则AC=OC.
∵OA=400米,
∴OC=OA cos45°=400×=200(米).
∵在直角△OBC中,∠COB=60°,OC=200米,
∴OB===400≈566(米)
故答案是:566.
4.解:如图,过点P作PQ⊥AB交AB延长线于点Q,过点M作MN⊥AB交AB延长线于点N,
在直角△AQP中,∠PAQ=45°,则AQ=PQ=60×1.5+BQ=90+BQ(海里),
所以 BQ=PQ﹣90.
在直角△BPQ中,∠BPQ=30°,则BQ=PQ tan30°=PQ(海里),
所以 PQ﹣90=PQ,
所以 PQ=45(3+)(海里)
所以 MN=PQ=45(3+)(海里)
在直角△BMN中,∠MBN=30°,
所以 BM=2MN=90(3+)(海里)
所以 =(小时)
故答案是:.
5.解:如图作BH⊥EF,CK⊥MN,垂足分别为H、K,则四边形BHCK是矩形,
设CK=HB=x,
∵∠CKA=90°,∠CAK=45°,
∴∠CAK=∠ACK=45°,
∴AK=CK=x,BK=HC=AK﹣AB=x﹣30,
∴HD=x﹣30+10=x﹣20,
在RT△BHD中,∵∠BHD=90°,∠HBD=30°,
∴tan30°=,
∴=,
解得x=30+10.
∴河的宽度为(30+10)米.
6.解:∵∠ACB=30°,∠ADB=60°,
∴∠CAD=30°,
∴AD=CD=60m,
在Rt△ABD中,
AB=AD sin∠ADB=60×=30(m).
故答案为:30.
7.解:过点O作OC垂直于AB的延长线于点C.
在Rt△COB中,∠BOC=37°,BC=OCtan37°,
在Rt△AOC中,∠AOC=60°,AC=OCtan60°=OC,
又∵AC=AB+BC,AB=100(km),
即OC=100+OC tan37°,
∴OC=≈102.2(千米).
故OC>100千米,这艘轮船可以不改变航向,不会触礁.
8.解:过点C作CP⊥AM.
∵AC=800米,∠MAC=30°,∠ACM=180°﹣(90°﹣30°+15°)=105°,
∴∠AMC=45°,
∴CP=PM=400米,AP=400米,
∴AM=400+400米,
∵AM PC=AC MN,
∴MN=200+200(米).
9.解:如图,过A作AH⊥BC,交CB的延长线于点H,
在Rt△ACD中,
∵∠CAD=30°,AD=150m,
∴CD=AD tan30°=150×=50(m),
∴AH=CD=50m.
在Rt△ABH中,
∵∠BAH=30°,AE=50m,
∴BH=AH tan30°=50×=50(m),
∴BC=AD﹣BH=150﹣50=100(m),
答:这栋楼的高度为100m.
故答案为:100.
10.解:如图,过A作AE⊥CD于E,
则AB=CE,
在△ACE中,∵∠AEC=90°,∠CAE=30°,EC=AB=21米,
∴AC=21×2=42(米),
∴AE===21≈35.7(米),
在Rt△ADE中,∵∠AED=90°,∠DAE=45°,
∴AE=DE=35.7米,
∴乙楼DC=CE+ED=21+35.7=56.7≈57(米).
答:乙楼的高约为57米.
11.解:延长AD交BC的延长线于E,作DF⊥BE于F,
∵∠BCD=150°,
∴∠DCF=30°,又CD=4米,
∴DF=2米,CF=(米),
由题意得∠E=45°,
∴EF=DF=2米,
∴BE=BC+CF+EF=5+2+2=(7+2)米,
∴AB=BE=7+2≈10.5(米),
故答案为10.5.
12.解:在Rt△BCD中,∠BDC=45°,
则BC=CD,
设BC=CD=x,则AC=x+8,
在Rt△ACD中,tan∠ADC==,
则x+8=x tan53°,
∴x+8=1.33x,
∴x≈24.2(m),
故建筑物BC的高约为24.2m,
故答案为:24.2.
13.解:在Rt△PBD中,tan∠BPD=,
则BD=PD tan∠BPD=20(米),
在Rt△PBD中,∠CPD=45°,
∴CD=PD=20(米),
∴BC=BD﹣CD=(20﹣20)米,
故答案为:(20﹣20).
14.解:如图,设CD为塔身的高,延长AB交CD于E,则CD=40,DE=7,
∴CE=33,
∵∠CBE=45°=∠BCE,∠CAE=30°,
∴BE=CE=33,
∴AE=a+33,
∵tanA=,
∴tan30°=,即33=a+33,
解得a=33(﹣1)≈24.1,
∴a的值约为24.1米,
故答案为:24.1.
15.解:由题意可得:∠BDA=45°,
则AB=AD=120m,
又∵∠CAD=30°,
∴在Rt△ADC中,
tan∠CAD=tan30°==,
解得:CD=40(m),
故答案为:40.
16.解:由于CD∥HB,
∴∠CAH=∠ACD=45°,∠B=∠BCD=30°
在Rt△ACH中,∵∴∠CAH=45°
∴AH=CH=1200米,
在Rt△HCB,∵tan∠B=
∴HB==
==1200(米).
∴AB=HB﹣HA
=1200﹣1200
=1200(﹣1)米
故答案为:1200(﹣1)
17.解:由题意可得:tan30°===,
解得:BD=30(m),
tan60°===,
解得:DC=90(m),
故该建筑物的高度为:BC=BD+DC=120≈208(m),
故答案为:208.
18.解:∵∠DBC=45°,
∴BC=CD,
tanα==,
则=,
解得CD=7(米).
故答案为:7.
19.解:如图,∠ABD=30°,∠ACD=45°,BC=100m,
设AD=xm,
在Rt△ACD中,∵tan∠ACD=,
∴CD=AD=x,
∴BD=BC+CD=x+100,
在Rt△ABD中,∵tan∠ABD=,
∴x=(x+100),
∴x=50(+1)≈137,
即山高AD为137米.
故答案为137.
20.解:在Rt△ACD中,CD=21m,∠DAC=30°,
则AC=CD≈36.3m;
在Rt△BCD中,∠DBC=45°,
则BC=CD=21m,
故AB=AC﹣BC=15.3m.
故答案为:15.3.
21.解:在BC上取点F,使∠FAE=50°,过点F作FH⊥AD于H,
∵BF∥EH,BE⊥AD,FH⊥AD,
∴四边形BEHF为矩形,
∴BF=EH,BE=FH,
∵斜坡AB的坡比为12:5,
∴=,
设BE=12xm,则AE=5xm,
由勾股定理得,AE2+BE2=AB2,即(5x)2+(12x)2=262,
解得,x=2,
∴AE=10m,BE=24m,
∴FH=BE=24m,
在Rt△FAH中,tan∠FAH=,
∴AH=≈20(m),
∴BF=EH=AH﹣AE=10(m),
∴坡顶B沿BC至少向右移10m时,才能确保山体不滑坡,
故答案为:10.
22.解:由题意可得:
∵∠ABO=70°,AB=6m,
∴sin70°==≈0.94,
解得:AO=5.64(m),
∵∠CDO=50°,DC=6m,
∴sin50°=≈0.77,
解得:CO=4.62(m),
则AC=5.64﹣4.62=1.02(m),
答:AC的长度约为1.02米.
故答案为:1.02.
23.解:分别过A、D作AF⊥BC,DG⊥BC,垂点分别为F、G,如图所示.
∵在Rt△ABF中,AB=12米,∠B=60°,
∴sin∠B=,
∴AF=12×=6(米),
∴DG=6(米).
∵在Rt△DGC中,CD=12米,DG=6米,
∴GC==18米.
∵在Rt△DEG中,tanE=,
∴=,
∴GE=26米,
∴CE=GE﹣CG=26﹣18=8(米).
即CE的长为8米.
故答案为8.
24.解:过点C作AB的延长线的垂线CE,即乘电梯从点B到点C上升的高度h,
已知∠ABC=135°,
∴∠CBE=180°﹣∠ABC=45°,
∴CE=BC sin∠CBE=5 sin45°=5 =5.
所以h=5,
故答案为:5.
25.解:由题意知:平滑前梯高为4 sin45°=4 =.
平滑后高为4 sin60°=4 =.
∴升高了2()m.
故答案为:2().
26.解:过D点作DF⊥BC,
设EF=xkm,则DF=xkm,BF=xkm,
在Rt△BFD中,BD==xkm,
∵D地在AB正中位置,
∴AB=2BD=xkm,
∵tan∠ABC=,
∴cos∠ABC=,
∴=,
解得x=3,
则BC=8km,AC=6km,AB=10km,
小张某天沿A→C→E→B→D→A路线跑一圈,他跑了8+10+6=24(km).
故答案为:24.
27.解:在Rt△CMB中,∵∠CMB=90°,MB=AM+AB=12米,∠MBC=30°,
∴CM=MB tan30°=12×=4,
在Rt△ADM中,∵∠AMD=90°,∠MAD=45°,
∴∠MAD=∠MDA=45°,
∴MD=AM=4米,
∴CD=CM﹣DM=(4﹣4)米,
故答案为:4﹣4.
28.解:AC=CD÷sin60°=6(米).
29.解:A关于x轴的对称点A′坐标是(0,﹣1)连接A′B,交x轴于点C,
作DB∥A′A,A′D∥OC,交DB于D,
故光线从点A到点B所经过的路程A′B===5.
30.解:过点A作AG⊥x轴,交x轴于点G.
∵B、C的坐标分别是(1,0)、(0,),
∴OC=,OB=1,
∴BC==2.
∵∠ABC=90°,∠BAC=30°,
∴AB====2.
∵∠ABG+∠CBO=90°,∠BCO+∠CBO=90°,
∴∠ABG=∠BCO.
∴sin∠ABG===,cos∠ABG===,
∴AG=,BG=3.
∴OG=1+3=4,
∴顶点A的坐标是(4,).
故答案为:(4,).
31.解:过点A作AM⊥y轴于点M,作AN⊥BN交于点N,
∵直线y=﹣2∥x轴,故∠ABN=α,
当sinα的值最大时,则tanα=值最大,
故BN最小,即BG最大时,tanα最大,
即当BG最大时,sinα的值最大,
设BG=y,
则AM=4,GC=n+2,CM=3﹣n,
∵∠ACM+∠MAC=90°,∠ACM+∠BCG=90°,
∴∠CAM=∠BCG,
∴tan∠CAM=tan∠BCG,
∴,即,
∴y=﹣(n﹣3)(n+2),
∵﹣<0,
故当n=(3﹣2)=时,y取得最大值,
故n=,
故答案为:.
32.解:给图中相关点标上字母,连接DE,如图所示.
在△ABC中,∠ABC=120°,BA=BC,
∴∠α=30°.
同理,可得出:∠CDE=∠CED=30°=∠α.
又∵∠AEC=60°,
∴∠AED=∠AEC+∠CED=90°.
设等边三角形的边长为a,则AE=2a,DE=2×sin60° a=a,
∴AD==a,
∴cos(α+β)==.
故答案为:.
33.解:连接BE,
∵点D是AB的中点,ED⊥AB,∠A=α,
∴ED是AB的垂直平分线,
∴EB=EA,
∴∠EBA=∠A=α,
∴∠BEC=2α,
∵tanα=,设DE=a,
∴AD=3a,AE=,
∴AB=6a,
∴BC=,AC=
∴CE=AC﹣AE=,
∴tan2α=,
故答案为:.
34.解:∵BC=6,sinA=,
∴AB=10,
∴AC==8,
∵D是AB的中点,
∴AD=AB=5,
∵△ADE∽△ACB,
∴=,即=,
解得:DE=.
故答案为:.
35.解:∵∠B=30°,∠ACB=90°,AB=14cm,
∴AC=7cm.
由题意可知BC∥ED,
∴∠AFC=∠ADE=45°,
∴AC=CF=7cm.
故S△ACF=×7×7=(cm2).
故答案为:.
36.解:方法1:设AC与BD交于点O,
∵AC、BD是正方形的对角线,
∴AC⊥BD,OA=OB,
在△BCE中,∠EBC=60°,∠OBC=45°,
∴∠EBO=60°﹣45°,
∴FO=tan(60°﹣45°) OB,
∴S△BOF=OF OB=tan(60°﹣45°) OB2,
∴S△BAF=S△BAO﹣S△BOF=﹣tan(60°﹣45°) OB2=﹣tan(60°﹣45°) OB2=OB2,
同理,得S△CGD=OB2,
∵S△CBE=sin60°=sin60°=AB2,
∴S ABCD﹣S△CBE﹣S△BAF﹣S△CGD=AB2﹣AB2﹣OB2,
∵OB=BD,BD2=AB2+AD2,AB=AD=1,
∴S ABCD﹣S△CBE﹣S△BAF﹣S△CGD=1﹣﹣(××(1+1)=,
图标中阴影部分图形AFEGD的面积=.
方法2:过G作GH⊥CD于H,
则易得△GDH是等腰直角三角形,设DH=GH=x,
∵△BEC是等边三角形,
∴∠BCE=60°,
∴∠ECD=90°﹣60°=30°,
∴CH=GH÷tan30°=x÷=x,
∵CD=DH+CH=1,
即x+x=1,
x(1+)=1,
解得x===,
∴S△CGD=×1×=
同理S△BFA=
易得S△BCE=
∴S阴影=S正方形ABCD﹣S△BCE﹣S△BAF﹣S△CGD
=1﹣﹣﹣
=.
故答案为:.
