北师大版八年级数学上册 1.1 蚂蚁怎样走最近课件(共18张PPT)
文档属性
| 名称 | 北师大版八年级数学上册 1.1 蚂蚁怎样走最近课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 615.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 14:17:48 | ||
图片预览





文档简介
(共18张PPT)
1.3 蚂蚁怎样走最近
2、已知 ABC中BC=41, AC=40, AB=9, 则此三角形为_______三角形, ______是最大角.
3、以 ABC的三条边为边长向外作正方形, 依次得到的面积是25, 144 , 169, 则这个三角形是______三角形.
1、三角形的三边分别是a,b,c, 且满足等式(a+b)2-c2=2ab, 则此三角形是:( )
A. 直角三角形; B. 是锐角三角形;
C.是钝角三角形; D. 是等腰直角三角形.
A
直角
∠ A
直角
创设情境 温故探新
我怎么走
会最近呢
有一个圆柱,它的高等于
12厘米,底面上圆的周长
等于18厘米,在圆柱下底
面上的A点有一只蚂蚁,
它想从点A爬到点B , 蚂
蚁沿着圆柱侧面爬行的
最短路程是多少 (π的
值取3)
A
B
C
创设情境 温故探新
1、有一圆柱形食品盒,它的高等于18cm,底面半径
为4cm, 蚂蚁爬行的速度为2cm/s.如果在盒外下底面的A
处有一只蚂蚁,它想吃到盒外对面中部点B处的食物,那
么它至少需要多少时间 (π取3 )
·
A·
·B
合作交流探究新知
2. 如图,一圆柱高4cm,底面半径0.5cm,一只蚂蚁从A
点绕圆柱的侧面一圈爬到点B处吃食,要爬行的最短
路程是是多少(结果π取3)
A·
B·
合作交流探究新知
A
B
A’
B
A
A’
r
O
h
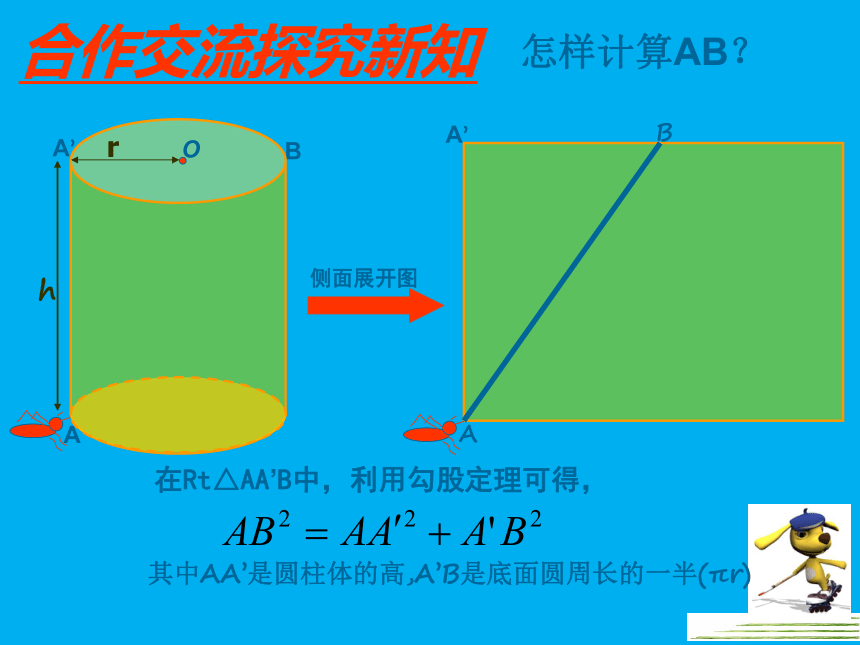
怎样计算AB?
在Rt△AA’B中,利用勾股定理可得,
侧面展开图
其中AA’是圆柱体的高,A’B是底面圆周长的一半(πr)
合作交流探究新知
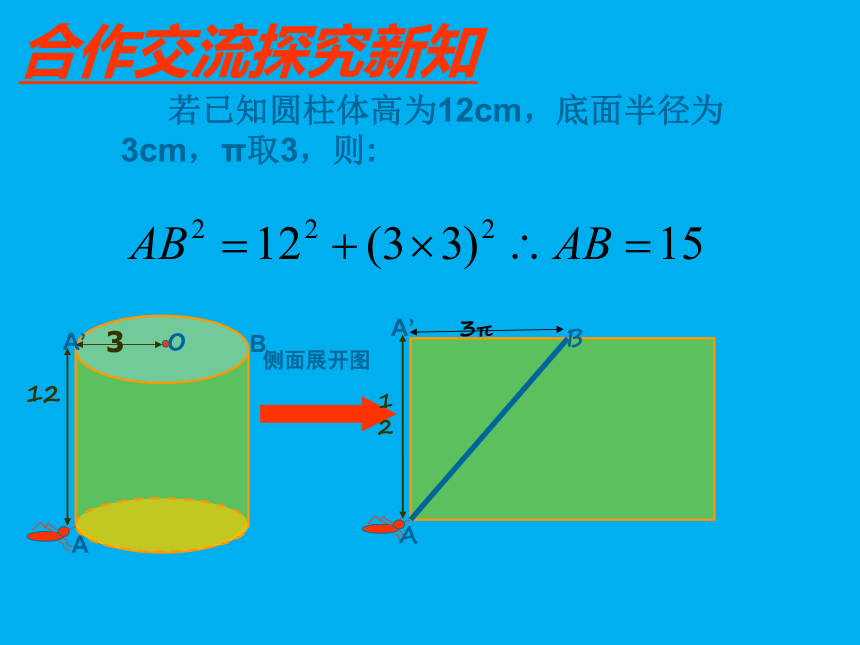
若已知圆柱体高为12cm,底面半径为3cm,π取3,则:
B
A
A’
3
O
12
侧面展开图
12
3π
A
A’
B
合作交流探究新知
合作交流探究新知
1.甲、乙两位探险者到沙漠进行探险,某日早晨8:00甲先出发,他以6km/h的速度向正东行走,1小时后乙出发,他以5km/h的速度向正北行走。上午10:00,甲、乙两人相距多远?
解:如图:已知A是甲、乙的出发点,10:00甲到达B点,乙到达C点.则:
AB=2×6=12(千米)
AC=1×5=5(千米)
在Rt△ABC中
∴BC=13(千米)
即甲乙两人相距13千米
反馈练习巩固新知
2.如图,台阶A处的蚂蚁要爬到B处搬运食物,它怎么走最近?并求出最近距离。
反馈练习巩固新知
甲、乙两位探险者到沙漠进行探险.某日早晨8:00甲先出发,他以6千米/小时的速度向东行走,1小时后乙出发,他以5千米/小时的速度向北行进,上午10:00,甲、乙二人相距多远
东
北
甲
乙
反馈练习巩固新知
有一个水池,水面是一个边长为10尺的正方形,在
水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根
芦苇拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池
的深度和这根芦苇的长度各是多少
5尺
1尺
x 尺
水池
反馈练习巩固新知
解:设水池的水深AC为x尺,则这根芦苇长为AD=AB=(x+1)尺,
在直角三角形ABC中,BC=5尺
由勾股定理得:BC2+AC2=AB2
即 52+ x2= (x+1)2
25+ x2= x2+2 x+1,
2 x=24,
∴ x=12, x+1=13
答:水池的水深12尺,这根芦苇长13尺。
5尺
x 尺
水池
反馈练习巩固新知
2、如图,有一个无盖长方体盒子,它的长是60厘米,宽和高都是40厘米,在A处有一只蚂蚁,它想吃到B点处的食物,那么它爬行的最短路程是多少?
A
B
A
B
C
100
40
AB2=BC2+AC2=1002+402=11600
∴AB≈108厘米
反馈练习巩固新知
2、如图,有一个长方体盒子,它的长是60厘米,宽和高都是40厘米,在A处有一只蚂蚁,它想吃到B点处的食物,那么它爬行的最短路程是多少?
A
B
A
B
60
80
c
AB2=AC2+BC2=602+802=1002
∴蚂蚁爬行的最短路程为100厘米。
反馈练习巩固新知
解:设水池的水深AC为x尺,则这根芦苇长为
AD=AB=(x+1)尺,
在直角三角形ABC中,BC=5尺
由勾股定理得:BC2+AC2=AB2
即 52+ x2= (x+1)2
25+ x2= x2+2 x+1,
2 x=24,
∴ x=12, x+1=13
答:水池的水深12尺,这根芦苇长13尺。
反馈练习巩固新知
课 堂 小 结
能说说运用勾股定理的知识
可以解决实际生活中哪些问题
2*.右图是学校的旗杆,旗杆上的绳子垂到了地面,并多出了一段,现在老师想知道旗杆的高度,能帮老师想个办法吗 请你与同伴交流设计方案
1.课本习题1.5第1,2,3题。
布置作业
1.3 蚂蚁怎样走最近
2、已知 ABC中BC=41, AC=40, AB=9, 则此三角形为_______三角形, ______是最大角.
3、以 ABC的三条边为边长向外作正方形, 依次得到的面积是25, 144 , 169, 则这个三角形是______三角形.
1、三角形的三边分别是a,b,c, 且满足等式(a+b)2-c2=2ab, 则此三角形是:( )
A. 直角三角形; B. 是锐角三角形;
C.是钝角三角形; D. 是等腰直角三角形.
A
直角
∠ A
直角
创设情境 温故探新
我怎么走
会最近呢
有一个圆柱,它的高等于
12厘米,底面上圆的周长
等于18厘米,在圆柱下底
面上的A点有一只蚂蚁,
它想从点A爬到点B , 蚂
蚁沿着圆柱侧面爬行的
最短路程是多少 (π的
值取3)
A
B
C
创设情境 温故探新
1、有一圆柱形食品盒,它的高等于18cm,底面半径
为4cm, 蚂蚁爬行的速度为2cm/s.如果在盒外下底面的A
处有一只蚂蚁,它想吃到盒外对面中部点B处的食物,那
么它至少需要多少时间 (π取3 )
·
A·
·B
合作交流探究新知
2. 如图,一圆柱高4cm,底面半径0.5cm,一只蚂蚁从A
点绕圆柱的侧面一圈爬到点B处吃食,要爬行的最短
路程是是多少(结果π取3)
A·
B·
合作交流探究新知
A
B
A’
B
A
A’
r
O
h
怎样计算AB?
在Rt△AA’B中,利用勾股定理可得,
侧面展开图
其中AA’是圆柱体的高,A’B是底面圆周长的一半(πr)
合作交流探究新知
若已知圆柱体高为12cm,底面半径为3cm,π取3,则:
B
A
A’
3
O
12
侧面展开图
12
3π
A
A’
B
合作交流探究新知
合作交流探究新知
1.甲、乙两位探险者到沙漠进行探险,某日早晨8:00甲先出发,他以6km/h的速度向正东行走,1小时后乙出发,他以5km/h的速度向正北行走。上午10:00,甲、乙两人相距多远?
解:如图:已知A是甲、乙的出发点,10:00甲到达B点,乙到达C点.则:
AB=2×6=12(千米)
AC=1×5=5(千米)
在Rt△ABC中
∴BC=13(千米)
即甲乙两人相距13千米
反馈练习巩固新知
2.如图,台阶A处的蚂蚁要爬到B处搬运食物,它怎么走最近?并求出最近距离。
反馈练习巩固新知
甲、乙两位探险者到沙漠进行探险.某日早晨8:00甲先出发,他以6千米/小时的速度向东行走,1小时后乙出发,他以5千米/小时的速度向北行进,上午10:00,甲、乙二人相距多远
东
北
甲
乙
反馈练习巩固新知
有一个水池,水面是一个边长为10尺的正方形,在
水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根
芦苇拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池
的深度和这根芦苇的长度各是多少
5尺
1尺
x 尺
水池
反馈练习巩固新知
解:设水池的水深AC为x尺,则这根芦苇长为AD=AB=(x+1)尺,
在直角三角形ABC中,BC=5尺
由勾股定理得:BC2+AC2=AB2
即 52+ x2= (x+1)2
25+ x2= x2+2 x+1,
2 x=24,
∴ x=12, x+1=13
答:水池的水深12尺,这根芦苇长13尺。
5尺
x 尺
水池
反馈练习巩固新知
2、如图,有一个无盖长方体盒子,它的长是60厘米,宽和高都是40厘米,在A处有一只蚂蚁,它想吃到B点处的食物,那么它爬行的最短路程是多少?
A
B
A
B
C
100
40
AB2=BC2+AC2=1002+402=11600
∴AB≈108厘米
反馈练习巩固新知
2、如图,有一个长方体盒子,它的长是60厘米,宽和高都是40厘米,在A处有一只蚂蚁,它想吃到B点处的食物,那么它爬行的最短路程是多少?
A
B
A
B
60
80
c
AB2=AC2+BC2=602+802=1002
∴蚂蚁爬行的最短路程为100厘米。
反馈练习巩固新知
解:设水池的水深AC为x尺,则这根芦苇长为
AD=AB=(x+1)尺,
在直角三角形ABC中,BC=5尺
由勾股定理得:BC2+AC2=AB2
即 52+ x2= (x+1)2
25+ x2= x2+2 x+1,
2 x=24,
∴ x=12, x+1=13
答:水池的水深12尺,这根芦苇长13尺。
反馈练习巩固新知
课 堂 小 结
能说说运用勾股定理的知识
可以解决实际生活中哪些问题
2*.右图是学校的旗杆,旗杆上的绳子垂到了地面,并多出了一段,现在老师想知道旗杆的高度,能帮老师想个办法吗 请你与同伴交流设计方案
1.课本习题1.5第1,2,3题。
布置作业
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
