2021-2022学年苏科版九年级数学下册6.4.1平行线分线段成比例及平行线截三角形相似--课后提升练(word解析版)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学下册6.4.1平行线分线段成比例及平行线截三角形相似--课后提升练(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览


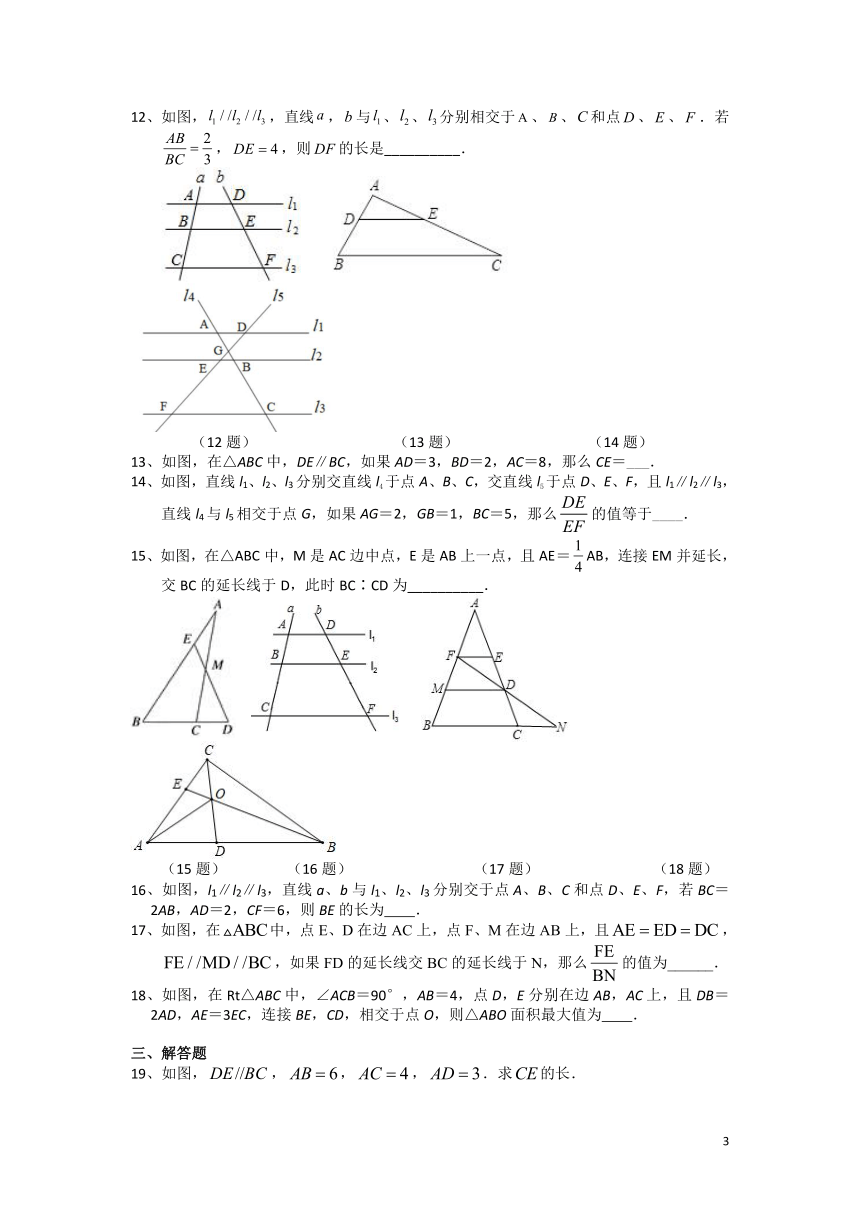


文档简介
6.4.1平行线分线段成比例及平行线截三角形相似--课后提升练
2021-2022学年苏科版九年级数学下册
一、选择题
1、如图,,直线a,b与分别相交于A,B,C和D,E,F.若,
则的长为( )
A.10 B. C.12 D.14
(1题) (2题) (3题) (4题)
2、如图,三条直线a∥b∥c,若,则=( )
A. B. C. D.
3、如图,在中,,若,,则的值为( )
A. B.2 C. D.
4、如图:在△ABC中,点D在BC边上,连接AD,GEBD且交AB于点E,GFAC且交CD于点F,则下列结论一定正确的是( )
A.= B.= C.= D.=
5、AD 是△ABC 的中线,E是AD 上一点,AE=AD,BE 的延长线交 AC 于 F,则的值为( )
A. B. C. D.
(5题) (6题) (7题)
6、如图,在 ABCD中,对角线AC、BD相交于点O,在DA的延长线上取点E,连接OE交AB于点F,已知AD=11,CD=14,且AF=2,则AE的长为( )
A.2.3 B.2.2 C.2.1 D.2
7、如图,在△ABC中,EF//BC,EG//AB,则下列式子一定正确的是( )
A. B. C. D.
8、如图,在梯形ABCD中,AD∥BC,点E、F分别在边AB、CD上,AD∥EF,如果AE:AB=1:3,
AD=4,BC=10,那么EF的长为( )
A. 5 B. 6 C. 7 D. 8
9、如图,在 ABCD中,AB=12,AD=8,∠ABC的平分线交CD于点F,交AD的延长线于点E,CG⊥BE,垂足为G,若EF=2,则线段CG的长为( )
A. B. C. D.
(9题) (10题) (11题)
10、如图所示,BE=3EC,D是线段AC的中点,BD和AE交于点F,已知△ABC的面积是7,
求四边形DCEF的面积( )
A.1 B. C. D.2
二、填空题
11、如图,△ABC中,点D、E分别在边AB,BC上,DE//AC,若DB=4,DA=2,BE=3,则EC=_________.
12、如图,,直线,与、、分别相交于、、和点、、.若,,则的长是__________.
(12题) (13题) (14题)
13、如图,在△ABC中,DE∥BC,如果AD=3,BD=2,AC=8,那么CE=___.
14、如图,直线l1、l2、l3分别交直线l4于点A、B、C,交直线l5于点D、E、F,且l1∥l2∥l3,直线l4与l5相交于点G,如果AG=2,GB=1,BC=5,那么的值等于____.
15、如图,在△ABC中,M是AC边中点,E是AB上一点,且AE=AB,连接EM并延长,交BC的延长线于D,此时BC∶CD为__________.
(15题) (16题) (17题) (18题)
16、如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别交于点A、B、C和点D、E、F,若BC=2AB,AD=2,CF=6,则BE的长为 .
17、如图,在中,点E、D在边AC上,点F、M在边AB上,且,,如果FD的延长线交BC的延长线于N,那么的值为______.
18、如图,在Rt△ABC中,∠ACB=90°,AB=4,点D,E分别在边AB,AC上,且DB=2AD,AE=3EC,连接BE,CD,相交于点O,则△ABO面积最大值为 .
三、解答题
19、如图,,,,.求的长.
20、如图,l1∥l2∥l3,AB=3,AD=2,DE=4,EF=7.5,求BC、BF的长.
21、如图,在中,D为AC上一点,E为CB的延长线上一点,连接BD交AB于点F,且,.求证:.
22、已知:如图,点、在的边上,点在边上,且,.
求证:.
23、已知:平行四边形,是延长线上一点,与、交于、.求证:.
24、如图,在中,是的中点,是边延长线上的点,连结交于点.
求证:.
25、如图,已知:正方形ABCD,点E在CB的延长线上,连接AE、DE,DE与边AB交于点F,FG∥BE交AE于点G.
(1)求证:GF=BF;
(2)若EB=1,BC=4,求AG的长;
(3)在BC边上取点M,使得BM=BE,连接AM交DE于点O.求证:FO ED=OD EF.
26、如图,在△ABC中,点D为BC上一点,点P在AD上,过点P作PM∥AC交AB于点M,作PN∥AB交AC于点N.
(1)若点D是BC的中点,
①若AP:PD=2:1,求AM:AB的值
②证明:;
(2)若点D是BC上任意一点,试证明:.
6.4.1平行线分线段成比例及平行线截三角形相似--课后提升练
2021-2022学年苏科版九年级数学下册(解析)
一、选择题
1、如图,,直线a,b与分别相交于A,B,C和D,E,F.若,
则的长为( )
A.10 B. C.12 D.14
【答案】D
【分析】
根据平行线分线段成比例的基本事实,建立比值关系求解即可.
【详解】
解:∵,且
∴, ∴
∴
故答案选:D
2、如图,三条直线a∥b∥c,若,则=( )
A. B. C. D.
【分析】
根据平行线分线段成比例的性质,即可求解.
【详解】
解:∵
∴
∴
故选B
3、如图,在中,,若,,则的值为( )
A. B.2 C. D.
【分析】
根据平行线分线段成比例定理可得.
【详解】
解:,,
,
故选:D.
4、如图:在△ABC中,点D在BC边上,连接AD,GEBD且交AB于点E,GFAC且交CD于点F,则下列结论一定正确的是( )
A.= B.= C.= D.=
【分析】
由GEBD、GFAC利用平行线分线段成比例,可得出,,进而可得出,此题得解.
【详解】
解:∵GEBD、GFAC,
∴,,
∴.
故选:C.
5、AD 是△ABC 的中线,E是AD 上一点,AE=AD,BE 的延长线交 AC 于 F,则的值为( )
A. B. C. D.
【分析】
作DG∥AC交BF于G,如图,根据平行线分线段成比例定理,由DG∥CF得
,即FC=2DG,由DG∥AF,,则,然后计算AF:FC.
【详解】
作DG∥AC交BF于G,如图,
∵AD是△ABC的中线,∴BD=CD,
∵DG∥CF,∴=,∴FC=2DG,
∵DG∥AF,∴,∴,
∴.
故选C.
6、如图,在 ABCD中,对角线AC、BD相交于点O,在DA的延长线上取点E,连接OE交AB于点F,已知AD=11,CD=14,且AF=2,则AE的长为( )
A.2.3 B.2.2 C.2.1 D.2
【分析】
过O点作OM∥AB,求出AM和MO的长,利用△AEF∽△MEO,得到关于AE的比例式,求出AE的长即可.
【详解】
解:过O点作OM∥AB,交AD于M,
∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD=14,
∴O为BD的中点,
又∵OM∥AB,
∴OM是△ABD的中位线,
∴AM=DM=AD=,OM=AB=7.
∵AF∥OM,
∴△AEF∽△MEO,
∴,
∴,
∴AE=.
故选B.
7、如图,在△ABC中,EF//BC,EG//AB,则下列式子一定正确的是( )
A. B. C. D.
【答案】D
【分析】根据平行线分线段成比例定理逐一判断即可.
【详解】∵EG//AB,EF//BC,∴,
∵AC≠EC∴不成立,∴选项A错误;
∵EG//AB,EF//BC,∴,,
∵AE≠EC,∴不成立,∴选项B错误;
∵EG//AB,EF//BC,∴,
∵DF≠AF∴不成立,∴选项C错误;
∵EG//AB,EF//BC,∴,,∴,∴选项D正确;
故选D.
8、如图,在梯形ABCD中,AD∥BC,点E、F分别在边AB、CD上,AD∥EF,如果AE:AB=1:3,
AD=4,BC=10,那么EF的长为( )
A. 5 B. 6 C. 7 D. 8
【答案】B
【解析】
【分析】连接BD交EF于点G,由平行线得出DF:DC=AE:AB=1:3,△BEG∽△BAD,△DFG∽△DCB,得出EG:4=2:3,GF:10=1:3,解得EG=,GF=,即可得出答案.
【详解】解:连接BD交EF于点G,
∵AE:AB=1:3,
∴EB:AB=2:3,
∵AD∥EF∥BC,
∴DF:DC=AE:AB=1:3,△BEG∽△BAD,△DFG∽△DCB,
∴EG:AD=EB:AB=2:3,GF:BC=DF:DC=1:3,
即EG:4=2:3,GF:10=1:3,
∴EG=,GF=,
∴EF=+=6.
故选B.
9、如图,在 ABCD中,AB=12,AD=8,∠ABC的平分线交CD于点F,交AD的延长线于点E,CG⊥BE,垂足为G,若EF=2,则线段CG的长为( )
A. B. C. D.
【详解】
∵∠ABC的平分线交CD于点F,∴∠ABE=∠CBE,
∵四边形ABCD是平行四边形,∴DC∥AB,
∴∠CBE=∠CFB=∠ABE=∠E,
∴CF=BC=AD=8,AE=AB=12,
∵AD=8,∴DE=4,
∵DC∥AB,∴,∴,∴EB=6,
∵CF=CB,CG⊥BF,∴BG=BF=2,
在Rt△BCG中,BC=8,BG=2,根据勾股定理得,CG===,
故选C.
10、如图所示,BE=3EC,D是线段AC的中点,BD和AE交于点F,已知△ABC的面积是7,
求四边形DCEF的面积( )
A.1 B. C. D.2
【答案】B
【解析】
【分析】
过点D作DH∥AE,交BC于H,先证得EH=CH,再证明,由此得到,根据BE=3CE求出△ACE的面积,即可得到答案.
【详解】过点D作DH∥AE,交BC于H,
∵点D是AC的中点,∴,即EH=CH,
∵BE=3CE,∴,∴,∴,
∵, ∴,
∵BE=3CE,∴, ∴四边形DCEF的面积=.
故选:B.
二、填空题
11、如图,△ABC中,点D、E分别在边AB,BC上,DE//AC,若DB=4,DA=2,BE=3,则EC=_________.
【详解】
试题分析:∵DE//AC,∴DB:AD=BE:CE,∴4:2=3:EC,EC=.
12、如图,,直线,与、、分别相交于、、和点、、.若,,则的长是__________.
【分析】
根据平行线分线段成比例定理列出比例式,把已知数据代入计算即可.
【详解】
解:∵,,
∴,即,
解得,,
∴,
故答案为:10.
13、如图,在△ABC中,DE∥BC,如果AD=3,BD=2,AC=8,那么CE=___.
【答案】
【解析】
【分析】根据平行线分线段成比例,可得,从而可以求得AE的长,进而即可求解.
【详解】解:∵DE∥BC,
∴,
∵AD=3,BD=2,AC=8,
∴,
∴AE=,
∴CE=AC-AE=8-=,
故答案是:.
14、如图,直线l1、l2、l3分别交直线l4于点A、B、C,交直线l5于点D、E、F,且l1∥l2∥l3,直线l4与l5相交于点G,如果AG=2,GB=1,BC=5,那么的值等于____.
【答案】
【解析】
【分析】根据平行线分线段成比例可得,代入计算,可求得答案.
【详解】解:∵AG=2,GB=1,
∴AB=AG+BG=3,
∵直线l1∥l2∥l3,
∴,
故答案是:.
15、如图,在△ABC中,M是AC边中点,E是AB上一点,且AE=AB,连接EM并延长,交BC的延长线于D,此时BC∶CD为__________.
【分析】
过C点作CP∥AB,交DE于P,由PC∥AE知,由AM=CM,得PC=AE,根据AE=AB得CP=AB,CP=BE,由CP∥BE得,可得BD=3CD,继而得到答案.
【详解】
过C点作CP∥AB,交DE于P,如图,
∵PC∥AE,
∴,
而AM=CM,
∴PC=AE,
∵AE=AB,
∴CP=AB,
∴CP=BE,
∵CP∥BE,
∴,
∴BD=3CD,
∴BC=2CD,即BC:CD为2:1,
故答案为2:1.
16、如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别交于点A、B、C和点D、E、F,若BC=2AB,AD=2,CF=6,则BE的长为 .
【分析】过A作DF的平行线,交BE于G,交CF于H,依据BG∥CH,即可得到,进而得出BE的长.
【解析】如图所示,过A作DF的平行线,交BE于G,交CF于H,
则AD=GE=HF=2,CH=6﹣2=4,
∵BG∥CH,
∴,即,
∴BG=,
∴BE=BG+GE=+2=,
故答案为:.
17、如图,在中,点E、D在边AC上,点F、M在边AB上,且,,如果FD的延长线交BC的延长线于N,那么的值为______.
【答案】
【解析】
【分析】
首先证明EF:BC=1:3,再利用全等三角形的性质证明即可解决问题.
【详解】
解:,, ,
又,,≌,,
::3,::4,,
故答案为.
18、如图,在Rt△ABC中,∠ACB=90°,AB=4,点D,E分别在边AB,AC上,且DB=2AD,AE=3EC,连接BE,CD,相交于点O,则△ABO面积最大值为 .
【分析】过点D作DF∥AE,根据平行线分线段成比例定理可得则,根据已知,可得DO=2OC,C在以AB为直径的圆上,设圆心为G,当CG⊥AB时,△ABC的面积最大为:×4×2=4,即可求出此时△ABO的最大面积.
【解析】如图,过点D作DF∥AE,
则,
∵,
∴DF=2EC,
∴DO=2OC,
∴DO=DC,
∴S△ADO=S△ADC,S△BDO=S△BDC,
∴S△ABO=S△ABC,
∵∠ACB=90°,
∴C在以AB为直径的圆上,设圆心为G,
当CG⊥AB时,△ABC的面积最大为:4×2=4,
此时△ABO的面积最大为:×4=.
故答案为:.
三、解答题
19、如图,,,,.求的长.
【答案】6
【分析】
根据平行线截线段成比例进行计算.
【详解】
解:,
,即,
,
.
20、如图,l1∥l2∥l3,AB=3,AD=2,DE=4,EF=7.5,求BC、BF的长.
【分析】
由平行线分线段成比例解答即可.
【详解】
∵l1∥l2∥l3,∴,
∵AB=3,AD=2,DE=4,∴,解得:BC=6,
∵l1∥l2∥l3,
∵AB=3,AD=2,DE=4,EF=7.5,
∴,∴,解得:BF=2.5.
21、如图,在中,D为AC上一点,E为CB的延长线上一点,连接BD交AB于点F,且,.求证:.
【解析】
【分析】
运用平行线分线段成比例定理式,结合已知条件得到,即可解决问题.
【详解】
∵,∴,,∵,∴,∴.
22、已知:如图,点、在的边上,点在边上,且,.
求证:.
【分析】
由平行线分线段成比例可以得到,
则根据等量代换可以推知,即.
【详解】
∵ ,∴ .
∵ ,∴ ,
∴ ,即.
23、已知:平行四边形,是延长线上一点,与、交于、.求证:.
【分析】
由平行四边形对边互相平行,可得平行线分线段成比例,得出比例式进行等比代换即可得证.
【详解】
解:∵四边形是平行四边形,
∴,.
∴,
∴,即.
24、如图,在中,是的中点,是边延长线上的点,连结交于点.
求证:.
【答案】见解析
【分析】
过点作交于,根据平行线分线段成比例定理和中点的性质得到,,利用等量代换得到答案.
【详解】
证明:过点作交于,
∴,
∵是的中点,∴,∴,
∵,∴,
∴.
25、如图,已知:正方形ABCD,点E在CB的延长线上,连接AE、DE,DE与边AB交于点F,FG∥BE交AE于点G.
(1)求证:GF=BF;
(2)若EB=1,BC=4,求AG的长;
(3)在BC边上取点M,使得BM=BE,连接AM交DE于点O.求证:FO ED=OD EF.
【分析】
(1)根据正方形的性质得到AD∥BC,AB∥CD,AD=CD,根据相似三角形的性质列出比例式,等量代换即可;
(2)根据勾股定理求出AE,根据相似三角形的性质计算即可;
(3)延长GF交AM于H,根据平行线分线段成比例定理得到,由于BM=BE,得到GF=FH,由GF∥AD,得到,等量代换得到,即,于是得到结论.
【详解】
解:(1)∵四边形ABCD是正方形,∴AD∥BC,AB∥CD,AD=CD,
∵GF∥BE,∴GF∥BC,∴GF∥AD,∴,
∵AB∥CD,,
∵AD=CD,∴GF=BF;
(2)∵EB=1,BC=4,
∴=4,AE=,
∴=4,
∴AG=;
(3)延长GF交AM于H,
∵GF∥BC,∴FH∥BC,∴,∴,
∵BM=BE,∴GF=FH,
∵GF∥AD,∴,,
∴, ∴,∴FO ED=OD EF.
26、如图,在△ABC中,点D为BC上一点,点P在AD上,过点P作PM∥AC交AB于点M,作PN∥AB交AC于点N.
(1)若点D是BC的中点,
①若AP:PD=2:1,求AM:AB的值
②证明:;
(2)若点D是BC上任意一点,试证明:.
【答案】(1)①;②见解析;(2)见解析.
【分析】
(1)①过点D作DE∥PM交AB于E,由点D为BC中点与AP:PD=2:1,根据平行线分线段成比例定理,即可求得AM:AB的值;
②延长AD至点Q,使DQ=AD,连BQ、CQ,易得四边形ABQC是平行四边形,由平行四边形的性质可得PM∥BQ,PN∥CQ,继而可得;
(2)过点D作DE∥PM交AB于E,即可得,又由PM∥AC,根据平行线分线段成比例定理可得,继而求得.
【详解】
(1)①过点D作DE∥PM交AB于E,
∵PM∥AC,∴DE∥AC,.
∵点D为BC中点,∴点E是AB中点,且,∴;
②延长AD至点Q,使DQ=AD,连BQ、CQ,
∵DQ=AD,BD=DC,四边形ABQC是平行四边形.
∴PM∥BQ,PN∥CQ,∴,,
∴;(注:像第(1)题那样作辅助线也可以.)
(3)过点D作DE∥PM交AB于E,∴,
又∵PM∥AC,∴DE∥AC,∴,
∴,
同理可得:,
∴.
2021-2022学年苏科版九年级数学下册
一、选择题
1、如图,,直线a,b与分别相交于A,B,C和D,E,F.若,
则的长为( )
A.10 B. C.12 D.14
(1题) (2题) (3题) (4题)
2、如图,三条直线a∥b∥c,若,则=( )
A. B. C. D.
3、如图,在中,,若,,则的值为( )
A. B.2 C. D.
4、如图:在△ABC中,点D在BC边上,连接AD,GEBD且交AB于点E,GFAC且交CD于点F,则下列结论一定正确的是( )
A.= B.= C.= D.=
5、AD 是△ABC 的中线,E是AD 上一点,AE=AD,BE 的延长线交 AC 于 F,则的值为( )
A. B. C. D.
(5题) (6题) (7题)
6、如图,在 ABCD中,对角线AC、BD相交于点O,在DA的延长线上取点E,连接OE交AB于点F,已知AD=11,CD=14,且AF=2,则AE的长为( )
A.2.3 B.2.2 C.2.1 D.2
7、如图,在△ABC中,EF//BC,EG//AB,则下列式子一定正确的是( )
A. B. C. D.
8、如图,在梯形ABCD中,AD∥BC,点E、F分别在边AB、CD上,AD∥EF,如果AE:AB=1:3,
AD=4,BC=10,那么EF的长为( )
A. 5 B. 6 C. 7 D. 8
9、如图,在 ABCD中,AB=12,AD=8,∠ABC的平分线交CD于点F,交AD的延长线于点E,CG⊥BE,垂足为G,若EF=2,则线段CG的长为( )
A. B. C. D.
(9题) (10题) (11题)
10、如图所示,BE=3EC,D是线段AC的中点,BD和AE交于点F,已知△ABC的面积是7,
求四边形DCEF的面积( )
A.1 B. C. D.2
二、填空题
11、如图,△ABC中,点D、E分别在边AB,BC上,DE//AC,若DB=4,DA=2,BE=3,则EC=_________.
12、如图,,直线,与、、分别相交于、、和点、、.若,,则的长是__________.
(12题) (13题) (14题)
13、如图,在△ABC中,DE∥BC,如果AD=3,BD=2,AC=8,那么CE=___.
14、如图,直线l1、l2、l3分别交直线l4于点A、B、C,交直线l5于点D、E、F,且l1∥l2∥l3,直线l4与l5相交于点G,如果AG=2,GB=1,BC=5,那么的值等于____.
15、如图,在△ABC中,M是AC边中点,E是AB上一点,且AE=AB,连接EM并延长,交BC的延长线于D,此时BC∶CD为__________.
(15题) (16题) (17题) (18题)
16、如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别交于点A、B、C和点D、E、F,若BC=2AB,AD=2,CF=6,则BE的长为 .
17、如图,在中,点E、D在边AC上,点F、M在边AB上,且,,如果FD的延长线交BC的延长线于N,那么的值为______.
18、如图,在Rt△ABC中,∠ACB=90°,AB=4,点D,E分别在边AB,AC上,且DB=2AD,AE=3EC,连接BE,CD,相交于点O,则△ABO面积最大值为 .
三、解答题
19、如图,,,,.求的长.
20、如图,l1∥l2∥l3,AB=3,AD=2,DE=4,EF=7.5,求BC、BF的长.
21、如图,在中,D为AC上一点,E为CB的延长线上一点,连接BD交AB于点F,且,.求证:.
22、已知:如图,点、在的边上,点在边上,且,.
求证:.
23、已知:平行四边形,是延长线上一点,与、交于、.求证:.
24、如图,在中,是的中点,是边延长线上的点,连结交于点.
求证:.
25、如图,已知:正方形ABCD,点E在CB的延长线上,连接AE、DE,DE与边AB交于点F,FG∥BE交AE于点G.
(1)求证:GF=BF;
(2)若EB=1,BC=4,求AG的长;
(3)在BC边上取点M,使得BM=BE,连接AM交DE于点O.求证:FO ED=OD EF.
26、如图,在△ABC中,点D为BC上一点,点P在AD上,过点P作PM∥AC交AB于点M,作PN∥AB交AC于点N.
(1)若点D是BC的中点,
①若AP:PD=2:1,求AM:AB的值
②证明:;
(2)若点D是BC上任意一点,试证明:.
6.4.1平行线分线段成比例及平行线截三角形相似--课后提升练
2021-2022学年苏科版九年级数学下册(解析)
一、选择题
1、如图,,直线a,b与分别相交于A,B,C和D,E,F.若,
则的长为( )
A.10 B. C.12 D.14
【答案】D
【分析】
根据平行线分线段成比例的基本事实,建立比值关系求解即可.
【详解】
解:∵,且
∴, ∴
∴
故答案选:D
2、如图,三条直线a∥b∥c,若,则=( )
A. B. C. D.
【分析】
根据平行线分线段成比例的性质,即可求解.
【详解】
解:∵
∴
∴
故选B
3、如图,在中,,若,,则的值为( )
A. B.2 C. D.
【分析】
根据平行线分线段成比例定理可得.
【详解】
解:,,
,
故选:D.
4、如图:在△ABC中,点D在BC边上,连接AD,GEBD且交AB于点E,GFAC且交CD于点F,则下列结论一定正确的是( )
A.= B.= C.= D.=
【分析】
由GEBD、GFAC利用平行线分线段成比例,可得出,,进而可得出,此题得解.
【详解】
解:∵GEBD、GFAC,
∴,,
∴.
故选:C.
5、AD 是△ABC 的中线,E是AD 上一点,AE=AD,BE 的延长线交 AC 于 F,则的值为( )
A. B. C. D.
【分析】
作DG∥AC交BF于G,如图,根据平行线分线段成比例定理,由DG∥CF得
,即FC=2DG,由DG∥AF,,则,然后计算AF:FC.
【详解】
作DG∥AC交BF于G,如图,
∵AD是△ABC的中线,∴BD=CD,
∵DG∥CF,∴=,∴FC=2DG,
∵DG∥AF,∴,∴,
∴.
故选C.
6、如图,在 ABCD中,对角线AC、BD相交于点O,在DA的延长线上取点E,连接OE交AB于点F,已知AD=11,CD=14,且AF=2,则AE的长为( )
A.2.3 B.2.2 C.2.1 D.2
【分析】
过O点作OM∥AB,求出AM和MO的长,利用△AEF∽△MEO,得到关于AE的比例式,求出AE的长即可.
【详解】
解:过O点作OM∥AB,交AD于M,
∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD=14,
∴O为BD的中点,
又∵OM∥AB,
∴OM是△ABD的中位线,
∴AM=DM=AD=,OM=AB=7.
∵AF∥OM,
∴△AEF∽△MEO,
∴,
∴,
∴AE=.
故选B.
7、如图,在△ABC中,EF//BC,EG//AB,则下列式子一定正确的是( )
A. B. C. D.
【答案】D
【分析】根据平行线分线段成比例定理逐一判断即可.
【详解】∵EG//AB,EF//BC,∴,
∵AC≠EC∴不成立,∴选项A错误;
∵EG//AB,EF//BC,∴,,
∵AE≠EC,∴不成立,∴选项B错误;
∵EG//AB,EF//BC,∴,
∵DF≠AF∴不成立,∴选项C错误;
∵EG//AB,EF//BC,∴,,∴,∴选项D正确;
故选D.
8、如图,在梯形ABCD中,AD∥BC,点E、F分别在边AB、CD上,AD∥EF,如果AE:AB=1:3,
AD=4,BC=10,那么EF的长为( )
A. 5 B. 6 C. 7 D. 8
【答案】B
【解析】
【分析】连接BD交EF于点G,由平行线得出DF:DC=AE:AB=1:3,△BEG∽△BAD,△DFG∽△DCB,得出EG:4=2:3,GF:10=1:3,解得EG=,GF=,即可得出答案.
【详解】解:连接BD交EF于点G,
∵AE:AB=1:3,
∴EB:AB=2:3,
∵AD∥EF∥BC,
∴DF:DC=AE:AB=1:3,△BEG∽△BAD,△DFG∽△DCB,
∴EG:AD=EB:AB=2:3,GF:BC=DF:DC=1:3,
即EG:4=2:3,GF:10=1:3,
∴EG=,GF=,
∴EF=+=6.
故选B.
9、如图,在 ABCD中,AB=12,AD=8,∠ABC的平分线交CD于点F,交AD的延长线于点E,CG⊥BE,垂足为G,若EF=2,则线段CG的长为( )
A. B. C. D.
【详解】
∵∠ABC的平分线交CD于点F,∴∠ABE=∠CBE,
∵四边形ABCD是平行四边形,∴DC∥AB,
∴∠CBE=∠CFB=∠ABE=∠E,
∴CF=BC=AD=8,AE=AB=12,
∵AD=8,∴DE=4,
∵DC∥AB,∴,∴,∴EB=6,
∵CF=CB,CG⊥BF,∴BG=BF=2,
在Rt△BCG中,BC=8,BG=2,根据勾股定理得,CG===,
故选C.
10、如图所示,BE=3EC,D是线段AC的中点,BD和AE交于点F,已知△ABC的面积是7,
求四边形DCEF的面积( )
A.1 B. C. D.2
【答案】B
【解析】
【分析】
过点D作DH∥AE,交BC于H,先证得EH=CH,再证明,由此得到,根据BE=3CE求出△ACE的面积,即可得到答案.
【详解】过点D作DH∥AE,交BC于H,
∵点D是AC的中点,∴,即EH=CH,
∵BE=3CE,∴,∴,∴,
∵, ∴,
∵BE=3CE,∴, ∴四边形DCEF的面积=.
故选:B.
二、填空题
11、如图,△ABC中,点D、E分别在边AB,BC上,DE//AC,若DB=4,DA=2,BE=3,则EC=_________.
【详解】
试题分析:∵DE//AC,∴DB:AD=BE:CE,∴4:2=3:EC,EC=.
12、如图,,直线,与、、分别相交于、、和点、、.若,,则的长是__________.
【分析】
根据平行线分线段成比例定理列出比例式,把已知数据代入计算即可.
【详解】
解:∵,,
∴,即,
解得,,
∴,
故答案为:10.
13、如图,在△ABC中,DE∥BC,如果AD=3,BD=2,AC=8,那么CE=___.
【答案】
【解析】
【分析】根据平行线分线段成比例,可得,从而可以求得AE的长,进而即可求解.
【详解】解:∵DE∥BC,
∴,
∵AD=3,BD=2,AC=8,
∴,
∴AE=,
∴CE=AC-AE=8-=,
故答案是:.
14、如图,直线l1、l2、l3分别交直线l4于点A、B、C,交直线l5于点D、E、F,且l1∥l2∥l3,直线l4与l5相交于点G,如果AG=2,GB=1,BC=5,那么的值等于____.
【答案】
【解析】
【分析】根据平行线分线段成比例可得,代入计算,可求得答案.
【详解】解:∵AG=2,GB=1,
∴AB=AG+BG=3,
∵直线l1∥l2∥l3,
∴,
故答案是:.
15、如图,在△ABC中,M是AC边中点,E是AB上一点,且AE=AB,连接EM并延长,交BC的延长线于D,此时BC∶CD为__________.
【分析】
过C点作CP∥AB,交DE于P,由PC∥AE知,由AM=CM,得PC=AE,根据AE=AB得CP=AB,CP=BE,由CP∥BE得,可得BD=3CD,继而得到答案.
【详解】
过C点作CP∥AB,交DE于P,如图,
∵PC∥AE,
∴,
而AM=CM,
∴PC=AE,
∵AE=AB,
∴CP=AB,
∴CP=BE,
∵CP∥BE,
∴,
∴BD=3CD,
∴BC=2CD,即BC:CD为2:1,
故答案为2:1.
16、如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别交于点A、B、C和点D、E、F,若BC=2AB,AD=2,CF=6,则BE的长为 .
【分析】过A作DF的平行线,交BE于G,交CF于H,依据BG∥CH,即可得到,进而得出BE的长.
【解析】如图所示,过A作DF的平行线,交BE于G,交CF于H,
则AD=GE=HF=2,CH=6﹣2=4,
∵BG∥CH,
∴,即,
∴BG=,
∴BE=BG+GE=+2=,
故答案为:.
17、如图,在中,点E、D在边AC上,点F、M在边AB上,且,,如果FD的延长线交BC的延长线于N,那么的值为______.
【答案】
【解析】
【分析】
首先证明EF:BC=1:3,再利用全等三角形的性质证明即可解决问题.
【详解】
解:,, ,
又,,≌,,
::3,::4,,
故答案为.
18、如图,在Rt△ABC中,∠ACB=90°,AB=4,点D,E分别在边AB,AC上,且DB=2AD,AE=3EC,连接BE,CD,相交于点O,则△ABO面积最大值为 .
【分析】过点D作DF∥AE,根据平行线分线段成比例定理可得则,根据已知,可得DO=2OC,C在以AB为直径的圆上,设圆心为G,当CG⊥AB时,△ABC的面积最大为:×4×2=4,即可求出此时△ABO的最大面积.
【解析】如图,过点D作DF∥AE,
则,
∵,
∴DF=2EC,
∴DO=2OC,
∴DO=DC,
∴S△ADO=S△ADC,S△BDO=S△BDC,
∴S△ABO=S△ABC,
∵∠ACB=90°,
∴C在以AB为直径的圆上,设圆心为G,
当CG⊥AB时,△ABC的面积最大为:4×2=4,
此时△ABO的面积最大为:×4=.
故答案为:.
三、解答题
19、如图,,,,.求的长.
【答案】6
【分析】
根据平行线截线段成比例进行计算.
【详解】
解:,
,即,
,
.
20、如图,l1∥l2∥l3,AB=3,AD=2,DE=4,EF=7.5,求BC、BF的长.
【分析】
由平行线分线段成比例解答即可.
【详解】
∵l1∥l2∥l3,∴,
∵AB=3,AD=2,DE=4,∴,解得:BC=6,
∵l1∥l2∥l3,
∵AB=3,AD=2,DE=4,EF=7.5,
∴,∴,解得:BF=2.5.
21、如图,在中,D为AC上一点,E为CB的延长线上一点,连接BD交AB于点F,且,.求证:.
【解析】
【分析】
运用平行线分线段成比例定理式,结合已知条件得到,即可解决问题.
【详解】
∵,∴,,∵,∴,∴.
22、已知:如图,点、在的边上,点在边上,且,.
求证:.
【分析】
由平行线分线段成比例可以得到,
则根据等量代换可以推知,即.
【详解】
∵ ,∴ .
∵ ,∴ ,
∴ ,即.
23、已知:平行四边形,是延长线上一点,与、交于、.求证:.
【分析】
由平行四边形对边互相平行,可得平行线分线段成比例,得出比例式进行等比代换即可得证.
【详解】
解:∵四边形是平行四边形,
∴,.
∴,
∴,即.
24、如图,在中,是的中点,是边延长线上的点,连结交于点.
求证:.
【答案】见解析
【分析】
过点作交于,根据平行线分线段成比例定理和中点的性质得到,,利用等量代换得到答案.
【详解】
证明:过点作交于,
∴,
∵是的中点,∴,∴,
∵,∴,
∴.
25、如图,已知:正方形ABCD,点E在CB的延长线上,连接AE、DE,DE与边AB交于点F,FG∥BE交AE于点G.
(1)求证:GF=BF;
(2)若EB=1,BC=4,求AG的长;
(3)在BC边上取点M,使得BM=BE,连接AM交DE于点O.求证:FO ED=OD EF.
【分析】
(1)根据正方形的性质得到AD∥BC,AB∥CD,AD=CD,根据相似三角形的性质列出比例式,等量代换即可;
(2)根据勾股定理求出AE,根据相似三角形的性质计算即可;
(3)延长GF交AM于H,根据平行线分线段成比例定理得到,由于BM=BE,得到GF=FH,由GF∥AD,得到,等量代换得到,即,于是得到结论.
【详解】
解:(1)∵四边形ABCD是正方形,∴AD∥BC,AB∥CD,AD=CD,
∵GF∥BE,∴GF∥BC,∴GF∥AD,∴,
∵AB∥CD,,
∵AD=CD,∴GF=BF;
(2)∵EB=1,BC=4,
∴=4,AE=,
∴=4,
∴AG=;
(3)延长GF交AM于H,
∵GF∥BC,∴FH∥BC,∴,∴,
∵BM=BE,∴GF=FH,
∵GF∥AD,∴,,
∴, ∴,∴FO ED=OD EF.
26、如图,在△ABC中,点D为BC上一点,点P在AD上,过点P作PM∥AC交AB于点M,作PN∥AB交AC于点N.
(1)若点D是BC的中点,
①若AP:PD=2:1,求AM:AB的值
②证明:;
(2)若点D是BC上任意一点,试证明:.
【答案】(1)①;②见解析;(2)见解析.
【分析】
(1)①过点D作DE∥PM交AB于E,由点D为BC中点与AP:PD=2:1,根据平行线分线段成比例定理,即可求得AM:AB的值;
②延长AD至点Q,使DQ=AD,连BQ、CQ,易得四边形ABQC是平行四边形,由平行四边形的性质可得PM∥BQ,PN∥CQ,继而可得;
(2)过点D作DE∥PM交AB于E,即可得,又由PM∥AC,根据平行线分线段成比例定理可得,继而求得.
【详解】
(1)①过点D作DE∥PM交AB于E,
∵PM∥AC,∴DE∥AC,.
∵点D为BC中点,∴点E是AB中点,且,∴;
②延长AD至点Q,使DQ=AD,连BQ、CQ,
∵DQ=AD,BD=DC,四边形ABQC是平行四边形.
∴PM∥BQ,PN∥CQ,∴,,
∴;(注:像第(1)题那样作辅助线也可以.)
(3)过点D作DE∥PM交AB于E,∴,
又∵PM∥AC,∴DE∥AC,∴,
∴,
同理可得:,
∴.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
