2021-2022学年华东师大版八年级数学上册13.2.5 边边边 同步测试卷 (word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版八年级数学上册13.2.5 边边边 同步测试卷 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 212.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览

文档简介
13.2.5 边边边同步测试卷 2021-2022学年华东师大版八年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共7小题,共21分)
用直尺和圆规作一个角等于已知角的作图痕迹如图所示,则作图的依据是()
A. B. C. D.
作AOB的平分线的作图过程如下:
做法如上图:
(1)在OA和OB上分别截取OD,OE,使OD=OE.
(2)分别以D,E为圆心、以大于DE的长为半径作弧,两弧在∠AOB内交于点C.
(3)作射线OC,则OC就是∠AOB的平分线.
用下面三角形全等的判定方法解释作图原理,其中最为恰当的是( )
A. 边角边 B. 角边角 C. 角角边 D. 边边边
如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是()
A. B.
C. D.
如图,已知AB=AC,BD=CD,E是AD上的一点,则下列结论中不成立的是()
A.
B.
C.
D.
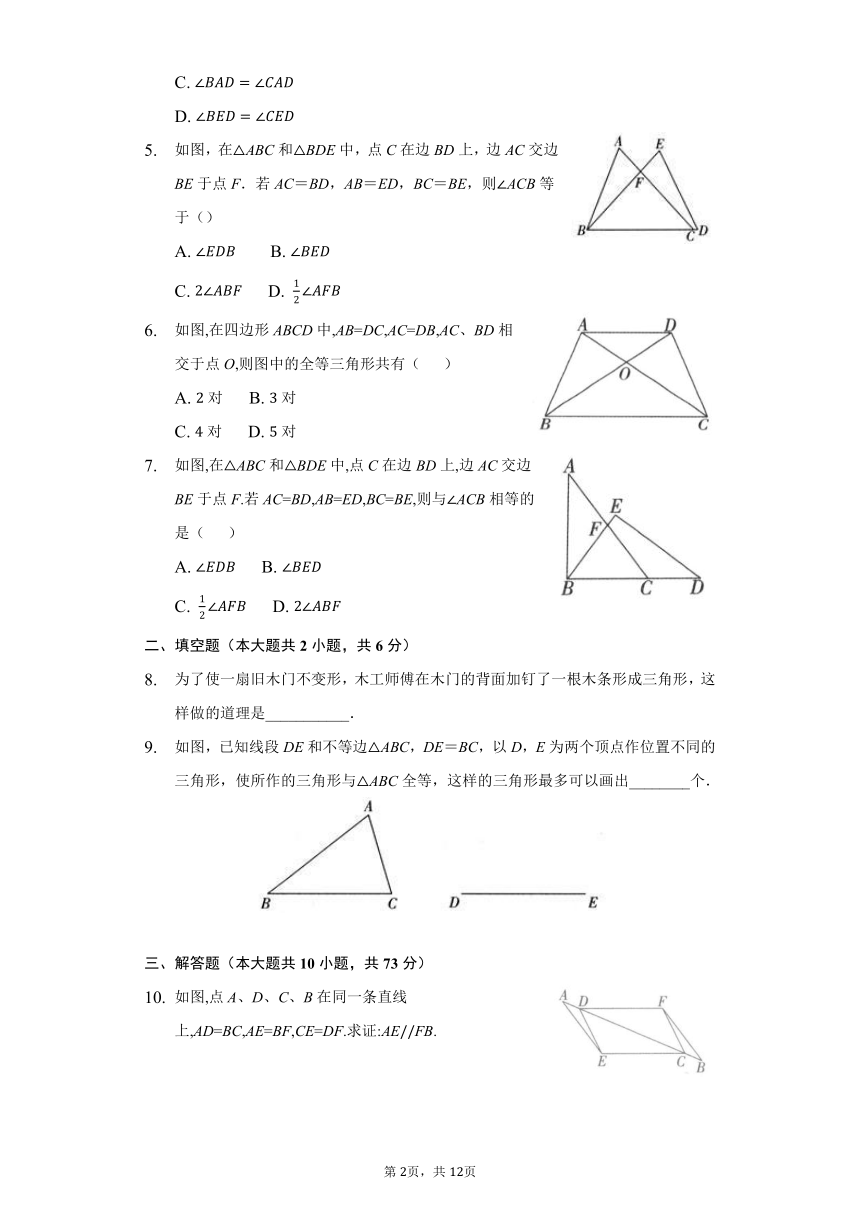
如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,则∠ACB等于()
A. B.
C. D.
如图,在四边形ABCD中,AB=DC,AC=DB,AC、BD相交于点O,则图中的全等三角形共有( )
A. 对 B. 对
C. 对 D. 对
如图,在ABC和BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,则与ACB相等的是( )
A. B.
C. D.
二、填空题(本大题共2小题,共6分)
为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条形成三角形,这样做的道理是___________.
如图,已知线段DE和不等边△ABC,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出________个.
三、解答题(本大题共10小题,共73分)
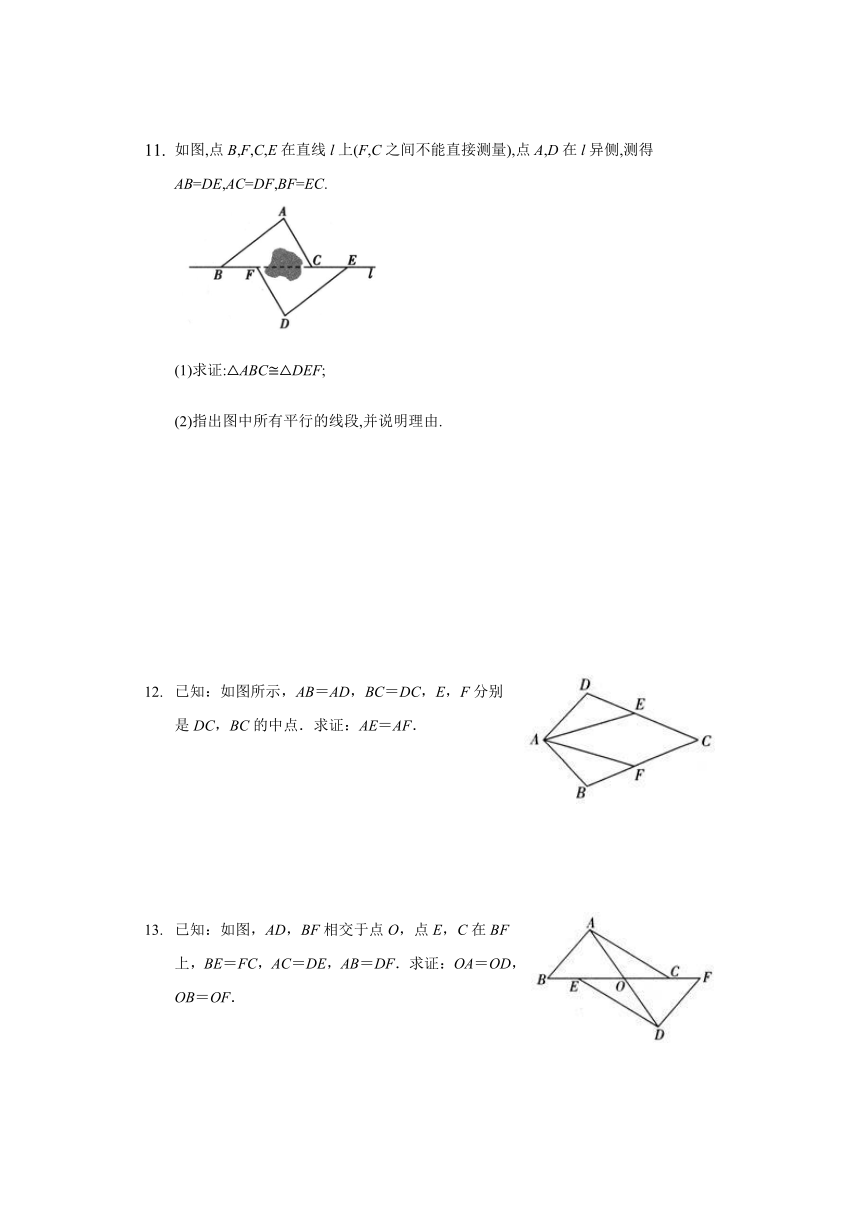
如图,点A、D、C、B在同一条直线上,AD=BC,AE=BF,CE=DF.求证:AEFB.
如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:ABCDEF;
(2)指出图中所有平行的线段,并说明理由.
已知:如图所示,AB=AD,BC=DC,E,F分别是DC,BC的中点.求证:AE=AF.
已知:如图,AD,BF相交于点O,点E,C在BF上,BE=FC,AC=DE,AB=DF.求证:OA=OD,OB=OF.
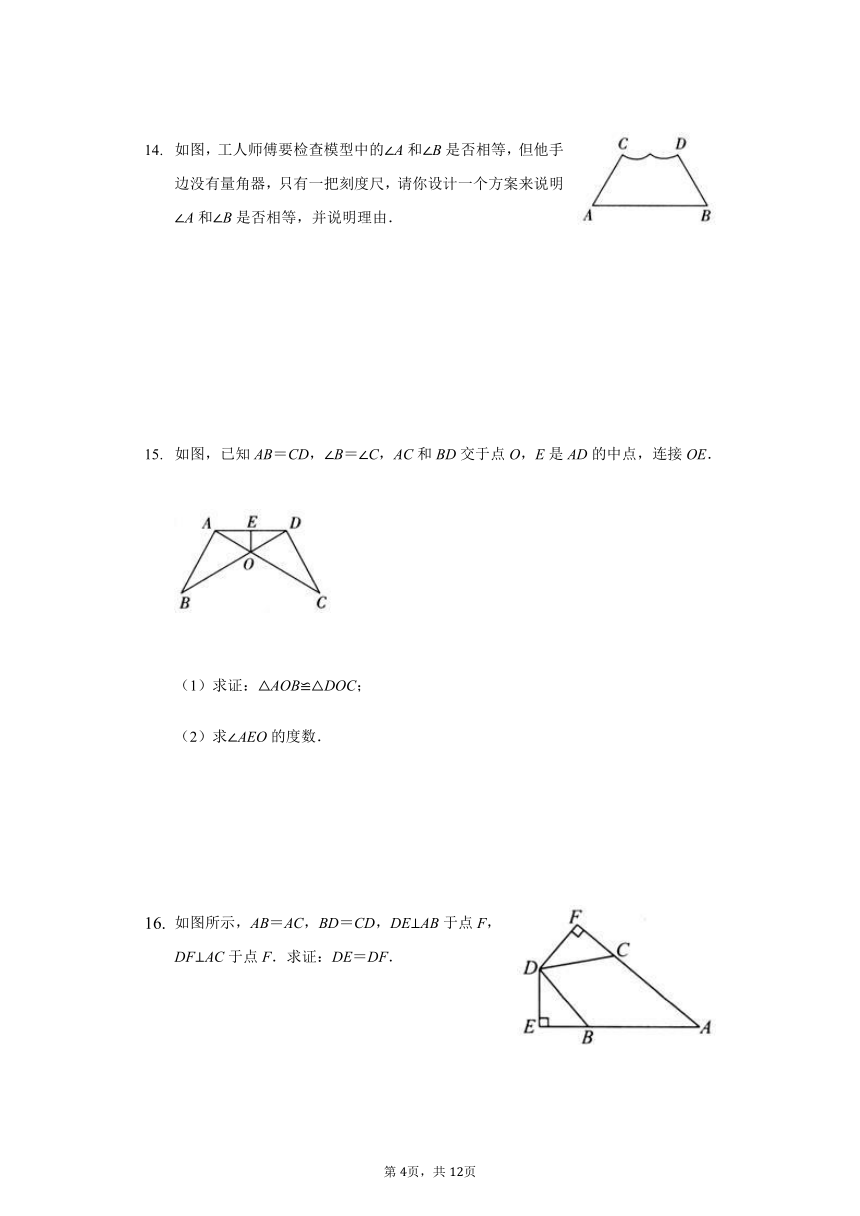
如图,工人师傅要检查模型中的∠A和∠B是否相等,但他手边没有量角器,只有一把刻度尺,请你设计一个方案来说明∠A和∠B是否相等,并说明理由.
如图,已知AB=CD,∠B=∠C,AC和BD交于点O,E是AD的中点,连接OE.
(1)求证:△AOB≌△DOC;
(2)求∠AEO的度数.
如图所示,AB=AC,BD=CD,DE⊥AB于点F,DF⊥AC于点F.求证:DE=DF.
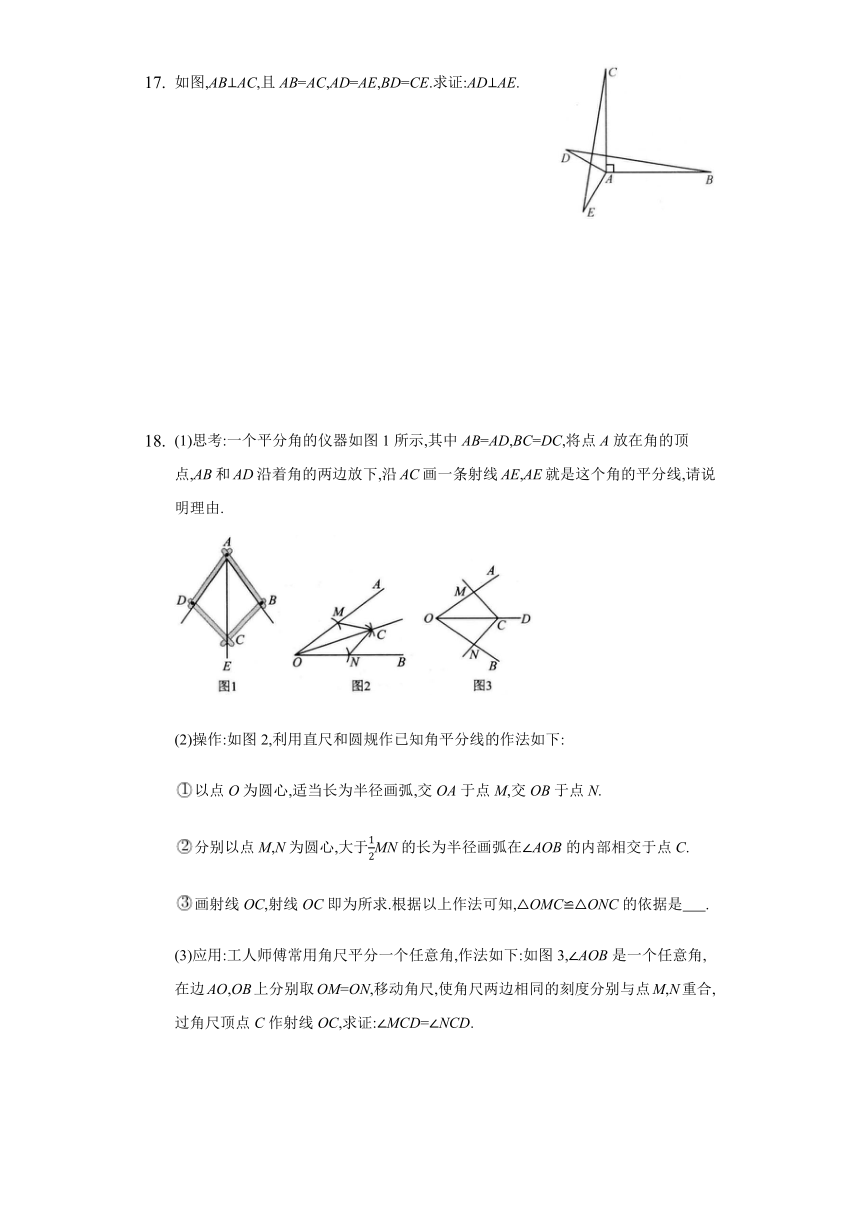
如图,ABAC,且AB=AC,AD=AE,BD=CE.求证:ADAE.
(1)思考:一个平分角的仪器如图1所示,其中AB=AD,BC=DC,将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是这个角的平分线,请说明理由.
(2)操作:如图2,利用直尺和圆规作已知角平分线的作法如下:
以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
分别以点M,N为圆心,大于MN的长为半径画弧在AOB的内部相交于点C.
画射线OC,射线OC即为所求.根据以上作法可知,OMCONC的依据是 .
(3)应用:工人师傅常用角尺平分一个任意角,作法如下:如图3,AOB是一个任意角,在边AO,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合,过角尺顶点C作射线OC,求证:MCD=NCD.
19.如图,将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.
(1)若固定三根木条AB,BC,AD不动,AB=AD=2cm,BC=5cm,量得第四根木条CD=5cm,判断此时B与D是否相等,并说明理由;
(2)若固定一根木条AB不动,AB=2cm,量得木条CD=5cm.如果木条AD,BC的长度不变,当点D移到BA的延长线上时,点C也在BA的延长线上;当点C移到AB的延长线上时,点A,C,D能构成周长为30cm的三角形.求出木条AD,BC的长度.
参考答案
1.【答案】A
2.【答案】D
3.【答案】C
4.【答案】B
5.【答案】D
6.【答案】B
7.【答案】C
8.【答案】三角形具有稳定性
9.【答案】4
10.【答案】证明:AD=BC,
AD+CD=BC+CD,即AC=BD.
在ACE和BDF中,
ACEBDF(SSS).
A=B.
AEFB.
11.【答案】(1)证明:BF=EC,
BF+FC=EC+CF,即BC=EF.
又AB=DE,AC=DF,
ABCDEF(SSS).
(2)解:ABDE,ACDF.
理由:ABCDEF,
ABC=DEF,ACB=DFE.
ABDE,ACDF.
12.【答案】证明:连接AC,
在△ACD和△ACB中,
∵
∴△ACD≌△ACB(SSS),
∴∠ACE=∠ACF.
∵DC=BC,E,F分别是DC,BC的中点,
∴CE=CF.
在△ACE和△ACF中,∵
∴△ACE≌△ACF(SAS),
∴AE=AF.
13.【答案】证明:∵BE=CF,
∴BE+EC=CF+EC,
∴BC=FE.
在△ABC和△DFE中,
∵
∴△ABC≌△DFE(SSS),
∴∠ABF=∠DFB.
在△ABO和△DFO中,
∵
∴△ABO≌△DFO(AAS),
∴OA=OD,OB=OF.
14.【答案】解:①如图,分别在AC和BD上取AE=BG;
②在AB上取AW=BF;
③量出WE的长为a米,FG的长为b米.
如果a=b,则说明∠A和∠B是相等的.
理由如下:在△AEW和△BGF中,
∴△AEW≌△BGF(SSS),
∴∠A=∠B.
15.【答案】证明:(1)在△AOB和△DOC中,
∵
∴△AOB≌△DOC(AAS);
解:(2)∵△AOB≌△DOC,
∴AO=DO.
∵E是AD的中点,
∴AE=DE.
在△AOE和△DOE中,
∴△AOE≌△DOE(SSS).
∴∠AEO=∠DEO.
∵∠AEO+∠DEO=180°,
∴∠AEO=∠DEO=90°.
16.【答案】证明:连接AD,如下图所示:
在△ACD和△ABD中,
,
∴△ACD≌△ABD(SSS),
∴∠EAD=∠FAD,
∴AD平分∠EAF,
又∵DE⊥AE,DF⊥AF,
∴DE=DF.
17.【答案】证明:在ABD和ACE中,
ABDACE(SSS).
EAC=DAB.
DAE=BAC.
ABAC,
BAC=.
DAE=,
即ADAE.
18.【答案】解:(1)在ABC和ADC中,
ABCADC(SSS).
BAC=DAC.
AE是BAD的平分线.
(2)SSS
(3)证明:在OMC和ONC中,
OMCONC(SSS).
MCO=NCO.
MCO+MCD=,NCO+NCD=,
MCD=NCD.
19.【答案】解:
(1)相等.理由:
如图,连结AC,
AB=AD,BC=DC,AC=AC,
ABCADC(SSS),B=D.
(2)设AD=x cm,BC=y cm,根据题意得,
当点D移到BA的延长线上,且点C在点D的右侧时,
解得
在ACD中,AD=13cm,CD=5cm,AC=12cm,
5+12>13,符合题意.
当点D移到BA的延长线上,且点C在点D的左侧时,
解得
在ACD中,AC=17cm,CD=5 cm,AD=8cm,
5+8<17,不合题意.
综上,AD=13cm,BC=10cm.
第2页,共3页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共7小题,共21分)
用直尺和圆规作一个角等于已知角的作图痕迹如图所示,则作图的依据是()
A. B. C. D.
作AOB的平分线的作图过程如下:
做法如上图:
(1)在OA和OB上分别截取OD,OE,使OD=OE.
(2)分别以D,E为圆心、以大于DE的长为半径作弧,两弧在∠AOB内交于点C.
(3)作射线OC,则OC就是∠AOB的平分线.
用下面三角形全等的判定方法解释作图原理,其中最为恰当的是( )
A. 边角边 B. 角边角 C. 角角边 D. 边边边
如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是()
A. B.
C. D.
如图,已知AB=AC,BD=CD,E是AD上的一点,则下列结论中不成立的是()
A.
B.
C.
D.
如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,则∠ACB等于()
A. B.
C. D.
如图,在四边形ABCD中,AB=DC,AC=DB,AC、BD相交于点O,则图中的全等三角形共有( )
A. 对 B. 对
C. 对 D. 对
如图,在ABC和BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,则与ACB相等的是( )
A. B.
C. D.
二、填空题(本大题共2小题,共6分)
为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条形成三角形,这样做的道理是___________.
如图,已知线段DE和不等边△ABC,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出________个.
三、解答题(本大题共10小题,共73分)
如图,点A、D、C、B在同一条直线上,AD=BC,AE=BF,CE=DF.求证:AEFB.
如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:ABCDEF;
(2)指出图中所有平行的线段,并说明理由.
已知:如图所示,AB=AD,BC=DC,E,F分别是DC,BC的中点.求证:AE=AF.
已知:如图,AD,BF相交于点O,点E,C在BF上,BE=FC,AC=DE,AB=DF.求证:OA=OD,OB=OF.
如图,工人师傅要检查模型中的∠A和∠B是否相等,但他手边没有量角器,只有一把刻度尺,请你设计一个方案来说明∠A和∠B是否相等,并说明理由.
如图,已知AB=CD,∠B=∠C,AC和BD交于点O,E是AD的中点,连接OE.
(1)求证:△AOB≌△DOC;
(2)求∠AEO的度数.
如图所示,AB=AC,BD=CD,DE⊥AB于点F,DF⊥AC于点F.求证:DE=DF.
如图,ABAC,且AB=AC,AD=AE,BD=CE.求证:ADAE.
(1)思考:一个平分角的仪器如图1所示,其中AB=AD,BC=DC,将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是这个角的平分线,请说明理由.
(2)操作:如图2,利用直尺和圆规作已知角平分线的作法如下:
以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
分别以点M,N为圆心,大于MN的长为半径画弧在AOB的内部相交于点C.
画射线OC,射线OC即为所求.根据以上作法可知,OMCONC的依据是 .
(3)应用:工人师傅常用角尺平分一个任意角,作法如下:如图3,AOB是一个任意角,在边AO,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合,过角尺顶点C作射线OC,求证:MCD=NCD.
19.如图,将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.
(1)若固定三根木条AB,BC,AD不动,AB=AD=2cm,BC=5cm,量得第四根木条CD=5cm,判断此时B与D是否相等,并说明理由;
(2)若固定一根木条AB不动,AB=2cm,量得木条CD=5cm.如果木条AD,BC的长度不变,当点D移到BA的延长线上时,点C也在BA的延长线上;当点C移到AB的延长线上时,点A,C,D能构成周长为30cm的三角形.求出木条AD,BC的长度.
参考答案
1.【答案】A
2.【答案】D
3.【答案】C
4.【答案】B
5.【答案】D
6.【答案】B
7.【答案】C
8.【答案】三角形具有稳定性
9.【答案】4
10.【答案】证明:AD=BC,
AD+CD=BC+CD,即AC=BD.
在ACE和BDF中,
ACEBDF(SSS).
A=B.
AEFB.
11.【答案】(1)证明:BF=EC,
BF+FC=EC+CF,即BC=EF.
又AB=DE,AC=DF,
ABCDEF(SSS).
(2)解:ABDE,ACDF.
理由:ABCDEF,
ABC=DEF,ACB=DFE.
ABDE,ACDF.
12.【答案】证明:连接AC,
在△ACD和△ACB中,
∵
∴△ACD≌△ACB(SSS),
∴∠ACE=∠ACF.
∵DC=BC,E,F分别是DC,BC的中点,
∴CE=CF.
在△ACE和△ACF中,∵
∴△ACE≌△ACF(SAS),
∴AE=AF.
13.【答案】证明:∵BE=CF,
∴BE+EC=CF+EC,
∴BC=FE.
在△ABC和△DFE中,
∵
∴△ABC≌△DFE(SSS),
∴∠ABF=∠DFB.
在△ABO和△DFO中,
∵
∴△ABO≌△DFO(AAS),
∴OA=OD,OB=OF.
14.【答案】解:①如图,分别在AC和BD上取AE=BG;
②在AB上取AW=BF;
③量出WE的长为a米,FG的长为b米.
如果a=b,则说明∠A和∠B是相等的.
理由如下:在△AEW和△BGF中,
∴△AEW≌△BGF(SSS),
∴∠A=∠B.
15.【答案】证明:(1)在△AOB和△DOC中,
∵
∴△AOB≌△DOC(AAS);
解:(2)∵△AOB≌△DOC,
∴AO=DO.
∵E是AD的中点,
∴AE=DE.
在△AOE和△DOE中,
∴△AOE≌△DOE(SSS).
∴∠AEO=∠DEO.
∵∠AEO+∠DEO=180°,
∴∠AEO=∠DEO=90°.
16.【答案】证明:连接AD,如下图所示:
在△ACD和△ABD中,
,
∴△ACD≌△ABD(SSS),
∴∠EAD=∠FAD,
∴AD平分∠EAF,
又∵DE⊥AE,DF⊥AF,
∴DE=DF.
17.【答案】证明:在ABD和ACE中,
ABDACE(SSS).
EAC=DAB.
DAE=BAC.
ABAC,
BAC=.
DAE=,
即ADAE.
18.【答案】解:(1)在ABC和ADC中,
ABCADC(SSS).
BAC=DAC.
AE是BAD的平分线.
(2)SSS
(3)证明:在OMC和ONC中,
OMCONC(SSS).
MCO=NCO.
MCO+MCD=,NCO+NCD=,
MCD=NCD.
19.【答案】解:
(1)相等.理由:
如图,连结AC,
AB=AD,BC=DC,AC=AC,
ABCADC(SSS),B=D.
(2)设AD=x cm,BC=y cm,根据题意得,
当点D移到BA的延长线上,且点C在点D的右侧时,
解得
在ACD中,AD=13cm,CD=5cm,AC=12cm,
5+12>13,符合题意.
当点D移到BA的延长线上,且点C在点D的左侧时,
解得
在ACD中,AC=17cm,CD=5 cm,AD=8cm,
5+8<17,不合题意.
综上,AD=13cm,BC=10cm.
第2页,共3页
