2021-2022学年人教版(2012)八年级上册14.2.2 完全平方公式 课后培优练习(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版(2012)八年级上册14.2.2 完全平方公式 课后培优练习(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 288.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览




文档简介
14.2.2 完全平方公式
一、单选题
1.已知,则的值等于( )
A.1 B.﹣1 C.0 D.
2.下列运算正确的是( )
A.(a+b)2=a2+b2 B.(-3x3)2=9x6
C. D.(a-b)2=a2-ab+b2
3.若x+4=2y,则代数式x2+4y2﹣4xy的值为( )
A.2 B.4 C.16 D.8
4.下列计算正确的是( )
A. B.
C. D.
5.有若干个大小形状完全相同的小长方形现将其中4个如图1摆放,构造出一个正方形,其中阴影部分面积为45;其中5个如图2摆放,构造出一个长方形,其中阴影部分面积为130(各个小长方形之间不重叠不留空),则每个小长方形的面积为( )
A.4 B.8 C.10 D.16
6.要使x2+kx+是完全平方式,那么k的值是( )
A.k= ±1 B.k= C.k=- D.k=
7.已知x+y=6,xy=4,则等于( )
A.28 B.-28 C.36 D.-36
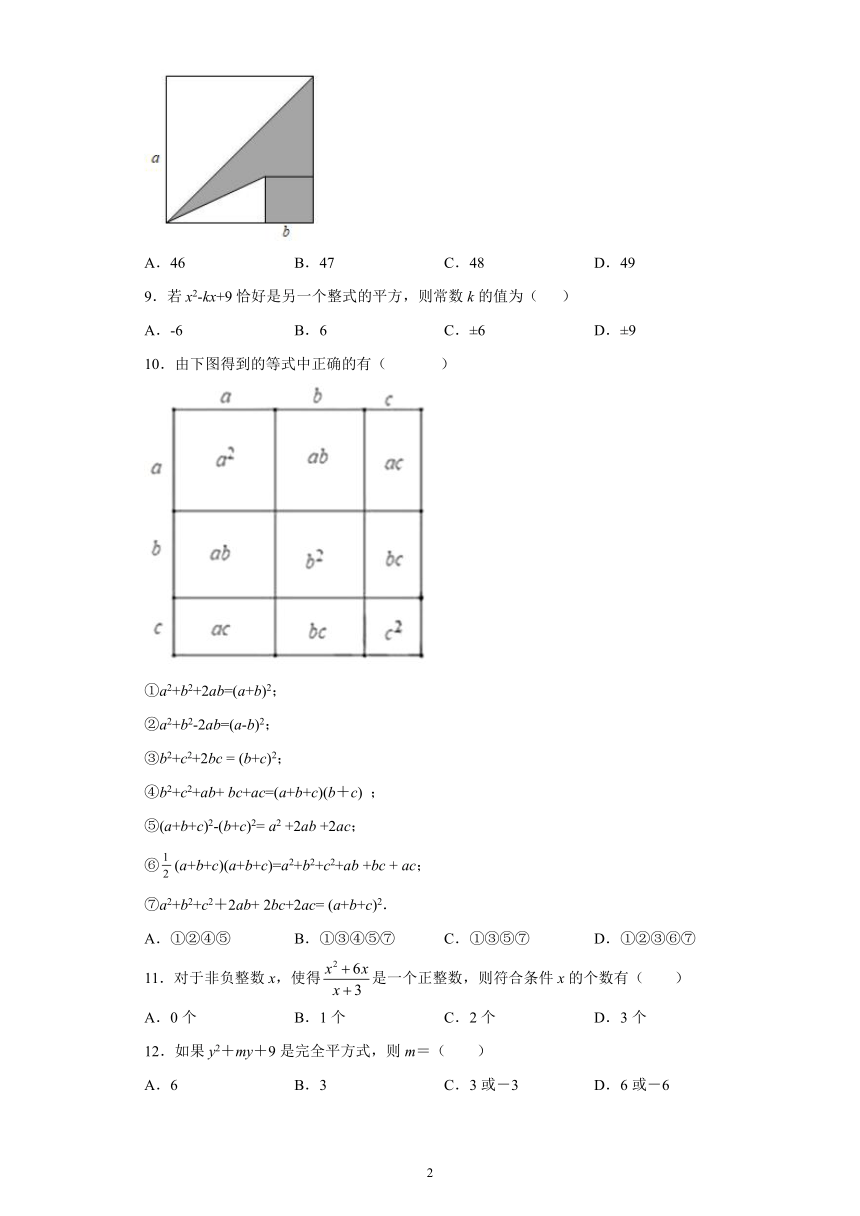
8.如图,两个正方形边长分别为a,b,已知,,则阴影部分的面积为( )
A.46 B.47 C.48 D.49
9.若x2-kx+9恰好是另一个整式的平方,则常数k的值为( )
A.-6 B.6 C.±6 D.±9
10.由下图得到的等式中正确的有( )
①a2+b2+2ab=(a+b)2;
②a2+b2-2ab=(a-b)2;
③b2+c2+2bc = (b+c)2;
④b2+c2+ab+ bc+ac=(a+b+c)(b+c) ;
⑤(a+b+c)2-(b+c)2= a2 +2ab +2ac;
⑥(a+b+c)(a+b+c)=a2+b2+c2+ab +bc + ac;
⑦a2+b2+c2+2ab+ 2bc+2ac= (a+b+c)2.
A.①②④⑤ B.①③④⑤⑦ C.①③⑤⑦ D.①②③⑥⑦
11.对于非负整数x,使得是一个正整数,则符合条件x的个数有( )
A.0个 B.1个 C.2个 D.3个
12.如果y2+my+9是完全平方式,则m=( )
A.6 B.3 C.3或-3 D.6或-6
二、填空题
13.x2+2x+a是一个完全平方式,则常数a的值为 ___.
14.已知,,则________,_________.
15.计算:______;______;______;______.
16.已知,则的值为________.
17.如图是数学教材第52页的图形,是用四个长和宽分别为a、b的全等长方形拼成的一个正方形(所拼图形无重叠、无缝隙),写出代数式(a+b)2、(a﹣b)2、ab之间的等量关系:__________________.
18.已知m2+km+81是完全平方式,则k=_____.
19.已知(a﹣b)2=6,(a+b)2=4,则a2+b2的值为 ___.
三、解答题
20.已知x2+3x-1=0,求4x(x+2)+(x-1)2-3(x2-1)的值.
21.已知的展开式中不含和项
(1)求的值
(2)求的值
22.已知在△ABC中,三边长a,b,c满足 a2+2b2+c2 2ab-2bc=0,请判断△ABC的形状,并证明你的结论.
23.化简求值.
(1)已知,,求和的值;
(2)已知,求代数式的值;
参考答案
1.B
解:∵,
∴,
∴,
∴,
解得m=-2,n=2,
∴=,
故选:B.
2.B
A. (a+b)2=a2+b2+2ab,故错误;
B. (-3x3)2=9x6, 故正确;
C. ,故错误;
D. (a-b)2=a2-2ab+b2, 故错误;
故答案选:B
3.C
解:∵x+4=2y,
∴ ,
∴.
故选:C
4.C
解:A、,故本选项错误,不符合题意;
B、,故本选项错误,不符合题意;
C、,故本选项正确,符合题意;
D、,故本选项错误,不符合题意;
故选:C
5.C
解:设长方形的长为a,宽为b,
由图1可得,(a+b)2-4ab=45,
即a2+b2=2ab+45①,
由图2可得,(2a+b)(a+2b)-5ab=130,
即a2+b2=65②,
由①②得,2ab+45=65,
所以ab=10,
即长方形的面积为10,
故选:C.
6.A
解:∵是完全平方式,
∴ ,
∴,
故选:A.
7.A
解:∵,
∴,
故选A.
8.B
解:由图可知,阴影部分的面积为,
,
,
,
将,代入得:,
即阴影部分的面积为47,
故选:B.
9.C
解:恰好是另一个整式的平方,
,
.
故选C.
10.C
①a2+b2+2ab=(a+b)2;根据左上4个四边形的面积可得,故①正确;
②a2+b2-2ab=(a-b)2;根据图形不可得到,故②不正确;
③b2+c2+2bc = (b+c)2;根据右下4个四边形的面积可得,故③正确;
④b2+c2+ab+ bc+ac=(a+b+c)(b+c) ;根据图形不可得到,故④不正确;
⑤(a+b+c)2-(b+c)2= a2 +2ab +2ac;根据大四边形的面积减去右下四个四边形的面积可得,故⑤正确
⑥(a+b+c)(a+b+c)=a2+b2+c2+ab +bc + ac;根据图形不可得到,故②不正确;
⑦a2+b2+c2+2ab+ 2bc+2ac= (a+b+c)2根据9个四边形的面积和可得,故⑦正确
故正确的有①③⑤⑦
故选C
11.B
,
,
,
,
为非负整数,是一个正整数,
的值只能为6,
即符合条件的个数有1个,
故选:B.
12.D
∵
∴
故选:D.
13.1
解:∵x2+2x+a是一个完全平方式,
∴a= =1,
故答案为:1.
14.12 ±7
解:∵
∴
∴
∴
∴
又
∴
故答案为:12,±7
15. 7
∵,
故答案为:;
∵7,
故答案为:7;
∵,
故答案为:;
∵,
故答案为:.
16.9
解:∵
∴
∴
故答案为:9
17.(a +b)2 =(a -b)2+4ab
解:由两个正方形及四个小长方形的面积关系可得:(a +b)2 =(a -b)2+4ab
故答案为(a +b)2 =(a -b)2+4ab.
18.或
解: m2+km+81
而m2+km+81是完全平方式,
或
故答案为:或
19.
解:,则①
,则②
①②得:
∴
故答案为
20.6
解:4x(x+2)+(x1)23(x21)
=4x2+8x+x22x+13x2+3
=2x2+6x+4
=2(x2+3x)+4,
∵x2+3x1=0,
∴x2+3x=1,
则原式=2+4=6.
21.(1),;(2).
解:(1)原式=
=
=
由于展开式中不含项和项,
∴且,
∴解得:,,
(2)由(1)可知:,,
∴,
∴,
∴,
∴
22.是等边三角形,证明见解析
解:△ABC是等边三角形,理由如下:
∵
∴
又∵,,
∴,
∴
∴是等边三角形
23.(1)17;21;(2)19.
解:(1)∵,,
∴,
;
(2),
,
,
,
∵,
∴原式.
一、单选题
1.已知,则的值等于( )
A.1 B.﹣1 C.0 D.
2.下列运算正确的是( )
A.(a+b)2=a2+b2 B.(-3x3)2=9x6
C. D.(a-b)2=a2-ab+b2
3.若x+4=2y,则代数式x2+4y2﹣4xy的值为( )
A.2 B.4 C.16 D.8
4.下列计算正确的是( )
A. B.
C. D.
5.有若干个大小形状完全相同的小长方形现将其中4个如图1摆放,构造出一个正方形,其中阴影部分面积为45;其中5个如图2摆放,构造出一个长方形,其中阴影部分面积为130(各个小长方形之间不重叠不留空),则每个小长方形的面积为( )
A.4 B.8 C.10 D.16
6.要使x2+kx+是完全平方式,那么k的值是( )
A.k= ±1 B.k= C.k=- D.k=
7.已知x+y=6,xy=4,则等于( )
A.28 B.-28 C.36 D.-36
8.如图,两个正方形边长分别为a,b,已知,,则阴影部分的面积为( )
A.46 B.47 C.48 D.49
9.若x2-kx+9恰好是另一个整式的平方,则常数k的值为( )
A.-6 B.6 C.±6 D.±9
10.由下图得到的等式中正确的有( )
①a2+b2+2ab=(a+b)2;
②a2+b2-2ab=(a-b)2;
③b2+c2+2bc = (b+c)2;
④b2+c2+ab+ bc+ac=(a+b+c)(b+c) ;
⑤(a+b+c)2-(b+c)2= a2 +2ab +2ac;
⑥(a+b+c)(a+b+c)=a2+b2+c2+ab +bc + ac;
⑦a2+b2+c2+2ab+ 2bc+2ac= (a+b+c)2.
A.①②④⑤ B.①③④⑤⑦ C.①③⑤⑦ D.①②③⑥⑦
11.对于非负整数x,使得是一个正整数,则符合条件x的个数有( )
A.0个 B.1个 C.2个 D.3个
12.如果y2+my+9是完全平方式,则m=( )
A.6 B.3 C.3或-3 D.6或-6
二、填空题
13.x2+2x+a是一个完全平方式,则常数a的值为 ___.
14.已知,,则________,_________.
15.计算:______;______;______;______.
16.已知,则的值为________.
17.如图是数学教材第52页的图形,是用四个长和宽分别为a、b的全等长方形拼成的一个正方形(所拼图形无重叠、无缝隙),写出代数式(a+b)2、(a﹣b)2、ab之间的等量关系:__________________.
18.已知m2+km+81是完全平方式,则k=_____.
19.已知(a﹣b)2=6,(a+b)2=4,则a2+b2的值为 ___.
三、解答题
20.已知x2+3x-1=0,求4x(x+2)+(x-1)2-3(x2-1)的值.
21.已知的展开式中不含和项
(1)求的值
(2)求的值
22.已知在△ABC中,三边长a,b,c满足 a2+2b2+c2 2ab-2bc=0,请判断△ABC的形状,并证明你的结论.
23.化简求值.
(1)已知,,求和的值;
(2)已知,求代数式的值;
参考答案
1.B
解:∵,
∴,
∴,
∴,
解得m=-2,n=2,
∴=,
故选:B.
2.B
A. (a+b)2=a2+b2+2ab,故错误;
B. (-3x3)2=9x6, 故正确;
C. ,故错误;
D. (a-b)2=a2-2ab+b2, 故错误;
故答案选:B
3.C
解:∵x+4=2y,
∴ ,
∴.
故选:C
4.C
解:A、,故本选项错误,不符合题意;
B、,故本选项错误,不符合题意;
C、,故本选项正确,符合题意;
D、,故本选项错误,不符合题意;
故选:C
5.C
解:设长方形的长为a,宽为b,
由图1可得,(a+b)2-4ab=45,
即a2+b2=2ab+45①,
由图2可得,(2a+b)(a+2b)-5ab=130,
即a2+b2=65②,
由①②得,2ab+45=65,
所以ab=10,
即长方形的面积为10,
故选:C.
6.A
解:∵是完全平方式,
∴ ,
∴,
故选:A.
7.A
解:∵,
∴,
故选A.
8.B
解:由图可知,阴影部分的面积为,
,
,
,
将,代入得:,
即阴影部分的面积为47,
故选:B.
9.C
解:恰好是另一个整式的平方,
,
.
故选C.
10.C
①a2+b2+2ab=(a+b)2;根据左上4个四边形的面积可得,故①正确;
②a2+b2-2ab=(a-b)2;根据图形不可得到,故②不正确;
③b2+c2+2bc = (b+c)2;根据右下4个四边形的面积可得,故③正确;
④b2+c2+ab+ bc+ac=(a+b+c)(b+c) ;根据图形不可得到,故④不正确;
⑤(a+b+c)2-(b+c)2= a2 +2ab +2ac;根据大四边形的面积减去右下四个四边形的面积可得,故⑤正确
⑥(a+b+c)(a+b+c)=a2+b2+c2+ab +bc + ac;根据图形不可得到,故②不正确;
⑦a2+b2+c2+2ab+ 2bc+2ac= (a+b+c)2根据9个四边形的面积和可得,故⑦正确
故正确的有①③⑤⑦
故选C
11.B
,
,
,
,
为非负整数,是一个正整数,
的值只能为6,
即符合条件的个数有1个,
故选:B.
12.D
∵
∴
故选:D.
13.1
解:∵x2+2x+a是一个完全平方式,
∴a= =1,
故答案为:1.
14.12 ±7
解:∵
∴
∴
∴
∴
又
∴
故答案为:12,±7
15. 7
∵,
故答案为:;
∵7,
故答案为:7;
∵,
故答案为:;
∵,
故答案为:.
16.9
解:∵
∴
∴
故答案为:9
17.(a +b)2 =(a -b)2+4ab
解:由两个正方形及四个小长方形的面积关系可得:(a +b)2 =(a -b)2+4ab
故答案为(a +b)2 =(a -b)2+4ab.
18.或
解: m2+km+81
而m2+km+81是完全平方式,
或
故答案为:或
19.
解:,则①
,则②
①②得:
∴
故答案为
20.6
解:4x(x+2)+(x1)23(x21)
=4x2+8x+x22x+13x2+3
=2x2+6x+4
=2(x2+3x)+4,
∵x2+3x1=0,
∴x2+3x=1,
则原式=2+4=6.
21.(1),;(2).
解:(1)原式=
=
=
由于展开式中不含项和项,
∴且,
∴解得:,,
(2)由(1)可知:,,
∴,
∴,
∴,
∴
22.是等边三角形,证明见解析
解:△ABC是等边三角形,理由如下:
∵
∴
又∵,,
∴,
∴
∴是等边三角形
23.(1)17;21;(2)19.
解:(1)∵,,
∴,
;
(2),
,
,
,
∵,
∴原式.
