湘教版八年级2021-2022学年八年级上册期末模拟练习3(含解析)
文档属性
| 名称 | 湘教版八年级2021-2022学年八年级上册期末模拟练习3(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
湘教版八年级2021-2022期末模拟练习3
姓名:__________班级:__________考号:__________总分__________
1 、选择题(本大题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
(2021年湖南省常德市)若,下列不等式不一定成立的是( )
A. B. C. D.
(2021年辽宁省盘锦市)下列运算正确的是( )
A. B. C. D.
对于任意三角形的高,下列说法不正确的是( )
A. 锐角三角形有三条高
B. 直角三角形只有一条高
C. 任意三角形都有三条高
D. 钝角三角形有两条高在三角形的外部
下列说法正确的是( )
A.两边和一角对应相等的两个三角形全等
B.面积相等的两三角形全等
C.有一边相等的两个等腰直角三角形全等
D.有两角和一边对应相等的两个三角形全等
估计+1的值( )
A.在1和2之间 B.在2和3之间 C.在3和4之间 D.在4和5之间
(2019年湖北省荆门市)﹣的倒数的平方是( )
A.2 B. C.﹣2 D.﹣
如图,已知∠CAB=∠DAB,则下列不能判定△ABC≌△ABD的条件是( )
A. ∠C=∠D B. AC=AD C. ∠CBA=∠DBA D. BC=BD
(2018年湖南省张家界市)若关于x的分式方程=1的解为x=2,则m的值为( )
A.5 B.4 C.3 D.2
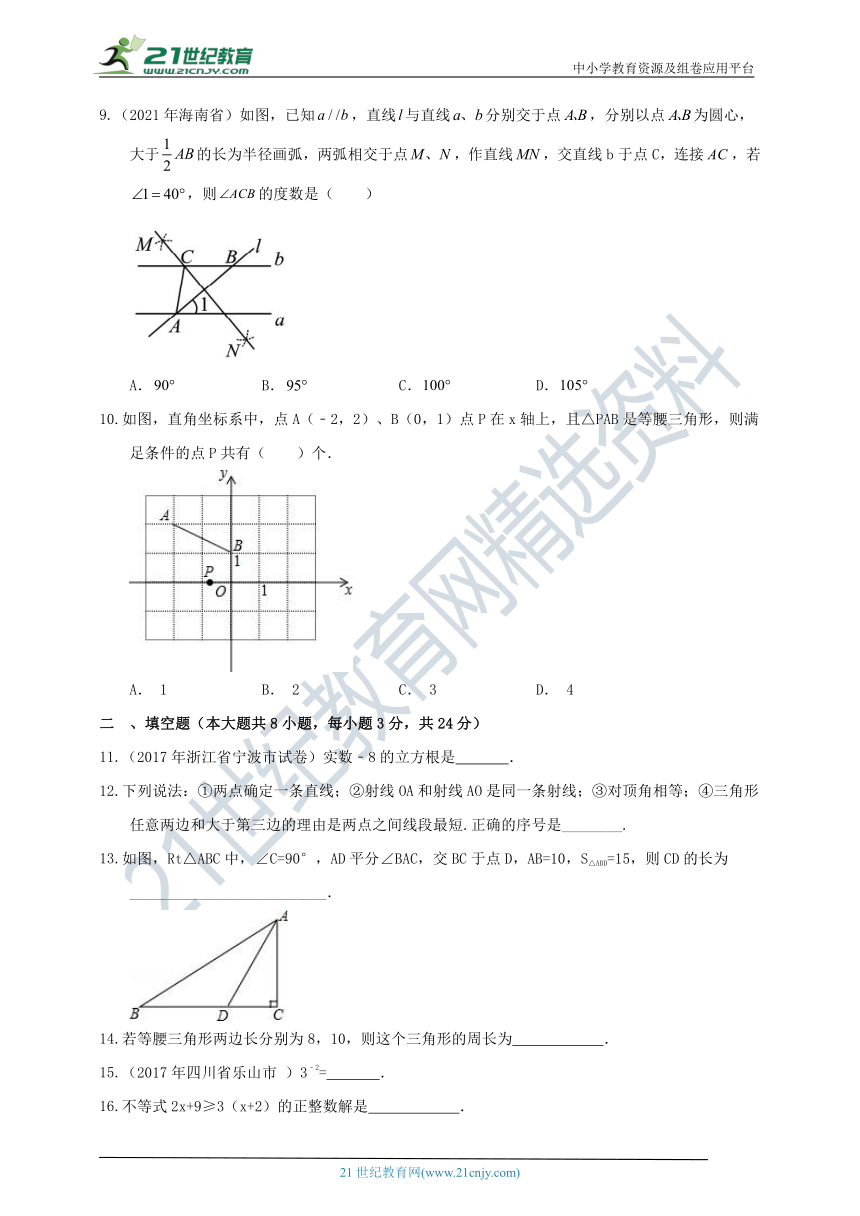
(2021年海南省)如图,已知,直线与直线分别交于点,分别以点为圆心,大于的长为半径画弧,两弧相交于点,作直线,交直线b于点C,连接,若,则的度数是( )
A. B. C. D.
如图,直角坐标系中,点A(﹣2,2)、B(0,1)点P在x轴上,且△PAB是等腰三角形,则满足条件的点P共有( )个.
A. 1 B. 2 C. 3 D. 4
1 、填空题(本大题共8小题,每小题3分,共24分)
(2017年浙江省宁波市试卷)实数﹣8的立方根是 .
下列说法:①两点确定一条直线;②射线OA和射线AO是同一条射线;③对顶角相等;④三角形任意两边和大于第三边的理由是两点之间线段最短.正确的序号是________.
如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为__________________________.
若等腰三角形两边长分别为8,10,则这个三角形的周长为 .
(2017年四川省乐山市 )3﹣2= .
不等式2x+9≥3(x+2)的正整数解是 .
(2021年湖北省荆州市)已知:,,则_____________.
(2018年贵州省遵义市)如图,△ABC中.点D在BC边上,BD=AD=AC,E为CD的中点.若∠CAE=16°,则∠B为 度.
1 、解答题(本大题共8小题,共66分)
(2017年江苏连云港市)化简: .
(2020年北京市)解不等式组:
(1)计算:①;②
(2)解方程组:
(2019年江苏省扬州)“绿水青山就是金山银山”,为了进一步优化河道环境,甲乙两工程队承担河道整治任务,甲、乙两个工程队每天共整治河道1500米,甲工程队整治3600米所用的时间与乙工程队整治2400米所用时间相等。甲工程队每天整治河道多少米?
如图方格纸中每个小正方形的边长均为1,点A,B在小正方形的顶点上.
(1)在图1中画出等腰钝角△ABC(点C在小正方形的顶点上),使△ABC的面积为2;
(2)在图2中画出等腰直角△ABC(点C在小正方形的顶点上),使∠ABC=90°.
(2020年江苏省徐州市)如图,,,.,与交于点.
(1)求证:;
(2)求的度数.
(2018年辽宁省阜新市)在运动会前夕,育红中学都会购买篮球、足球作为奖品.若购买10个篮球和15个足球共花费3000元,且购买一个篮球比购买一个足球多花50元.
(1)求购买一个篮球,一个足球各需多少元?
(2)今年学校计划购买这种篮球和足球共10个,恰逢商场在搞促销活动,篮球打九折,足球打八五折,若此次购买两种球的总费用不超过1050元,则最多可购买多少个篮球?
已知点A在x轴正半轴上,以OA为边作等边OAB,A(x,0),其中x是方程的解.
(1)求点A的坐标;
(2)如图1,点C在y轴正半轴上,以AC为边在第一象限内作等边ACD,连DB并延长交y轴于点E,求的度数;
(3)如图2,点F为x轴正半轴上一动点,点F在点A的右边,连接FB,以FB为边在第一象限内作等边FBG,连GA并延长交y轴于点H,当点F运动时,的值是否发生变化?若不变,求其值;若变化,求出其变化的范围.
答案解析
1 、选择题
【考点】不等式的性质
【分析】根据不等式的性质逐项进行判断即可得到答案.
解:A.在不等式两边同时减去5,不等式仍然成立,即,故选项A不符合题意;
B. 在不等式两边同时除以-5,不等号方向改变,即,故选项B不符合题意;
C.当c≤0时,不等得到,故选项C符合题意;
D. 在不等式两边同时加上c,不等式仍然成立,即,故选项D不符合题意;
故选:C.
【点评】此题主要考查了不等式的性质运用的,熟练掌握不等式的性质是解答此题的关键.
【考点】合并同项类,负整数指数幂,积的乘方,单项式除以单项式
【分析】利用合并同项类,负整数指数幂的运算法则,积的乘方的法则,单项式除以单项式的法则对各选项进行运算即可.
解:、和不是同类项,不能合并,故不符合题意;
、,故不符合题意;
、,故不符合题意;
、,故符合题意.
故选:.
【点评】本题主要考查合并同类项,积的乘方,负整数指数幂,单项式除以单项式,解答的关键是对合并同类项的法则,积的乘方的法则,负整数指数幂的法则,单项式除以单项式的法则的掌握与运用.
【考点】三角形的角平分线、中线和高.
【分析】 根据三角形的高的概念,通过具体作高,发现:任意一个三角形都有三条高,其中锐角三角形的三条高都在三角形的内部;直角三角形有两条高即三角形的两条直角边,一条在内部;钝角三角形有两条高在三角形的外部,一条在内部,据此解答即可.
解:A.锐角三角形有三条高,说法正确,故本选项不符合题意;
B、直角三角形有三条高,说法错误,故本选项符合题意;
C、任意三角形都有三条高,说法正确,故本选项不符合题意;
D、钝角三角形有两条高在三角形的外部,说法正确,故本选项不符合题意;
故选B.
【点评】本题考查了三角形的高:从三角形的一个顶点向它的对边作垂线,垂足与顶点之间的线段叫做三角形的高,注意不同形状的三角形的高的位置.
【考点】全等三角形的判定.
【分析】从各选项提供的已知进行思考,运用判定方法逐一验证,其中D是能够判定三角形全等的,其它选项是错误的.
解:A.两边和一角对应相等,错误,角的位置不确定,而SSA不能确定;
B、错误,面积相等的两三角形不一定重合,不能确定;
C、可能是一个三角形的直角边等于另一个三角形的斜边,故错误;
D、正确,ASA或AAS都能确定.
故选D.
【点评】本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA.SAS、SSS,直角三角形可用HL定理,但AAA.SSA,无法证明三角形全等.在叙述或运用定理时一定要注意位置对应.
【考点】估算无理数的大小.
【分析】直接利用已知无理数得出的取值范围,进而得出答案.
解:∵2<<3,
∴3<+1<4,
∴+1在在3和4之间.
故选:C.
【点评】此题主要考查了估算无理数大小,正确得出的取值范围是解题关键.
【考点】二次根式的性质,算术平方根,实数的性质
【分析】根据倒数,平方的定义以及二次根式的性质化简即可.
解:﹣的倒数的平方为:.
故选:B.
【点评】本题考查了倒数的定义、平方的定义以及二次根式的性质,是基础题,熟记概念是解题的关键
【考点】 全等三角形的判定.
【分析】根据全等三角形的判定定理(SAS,ASA,AAS,SSS)判断即可.
解:A.∵∠D=∠C,∠DAB=∠CAB,AB=AB,
∴根据AAS能推出△ABC≌△ABD,故本选项错误;
B、∵AD=AC,∠DAB=∠CAB,AB=AB,
∴根据SAS能推出△ABC≌△ABD,故本选项错误;
C、∵∠DAB=∠CAB,AB=AB,∠ABD=∠ABC,
∴根据ASA能推出△ABC≌△ABD,故本选项错误;
D、根据BD=BC,AB=AB,∠DAB=∠CAB不能推出△ABC≌△ABD,故本选项正确;
故选D.
【点评】 本题考查了全等三角形判定定理的应用,注意:全等三角形的判定定理有:SAS,ASA,AAS,SSS.
【考点】分式方程的解
【分析】直接解分式方程进而得出答案.
解:∵关于x的分式方程=1的解为x=2,
∴x=m﹣2=2,
解得:m=4.
故选:B.
【点评】此题主要考查了分式方程的解,正确解方程是解题关键.
【考点】线段垂直平分线的作法及性质,平行线的性质,等腰三角形的性质
【分析】根据题意可得直线是线段AB的垂直平分线,进而可得,利用平行线的性质及等腰三角形中等边对等角,可得,所以可求得.
解:∵已知分别以点为圆心,大于的长为半径画弧,两弧相交于点,作直线,交直线b于点C,连接,
∴直线垂直平分线段AB,
∴,
∵,,
∴,
∴,
∴.
故选:C.
【点评】题目主要考查线段垂直平分线的作法及性质、平行线的性质等,根据题意得出直线垂直平分线段AB是解题关键.
【考点】等腰三角形的判定;坐标与图形性质.
【分析】由AB=AP,可得以A为圆心,AB为半径画圆,交x轴有二点P1(﹣1,0),P2(﹣3,0);
由BP=AB,可得以B为圆心,BA为半径画圆,交x轴有二点P3(﹣2,0),(2,0)不能组成△ABP,
由AP=BP,可得AB的垂直平分线交x轴一点P4(PA=PB).
解:如图,点A(﹣2,2)、B(0,1),
①以A为圆心,AB为半径画圆,交x轴有二点P1(﹣1,0),P2(﹣3,0),此时(AP=AB);
②以B为圆心,BA为半径画圆,交x轴有二点P3(﹣2,0),(2,0)不能组成△ABP,故舍去,此时(BP=AB);
③AB的垂直平分线交x轴一点P4(PA=PB),此时(AP=BP);
设此时P4(x,0),
则(x+2)2+4=x2+1,
解得:x=﹣,
∴P4(﹣,0).
∴符合条件的点有4个.
故选D.
【点评】此题考查了等腰三角形的判定.此题那难度适中,注意掌握数形结合思想与分类讨论思想的应用.
1 、填空题
【考点】立方根.
【分析】利用立方根的定义即可求解.
解:∵(﹣2)3=﹣8,
∴﹣8的立方根是﹣2.
故答案﹣2.
【点评】本题主要考查了立方根的概念.如果一个数x的立方等于a,即x的三次方等于a(x3=a),那么这个数x就叫做a的立方根,也叫做三次方根.
【考点】直线、射线、线段,三角形三边的关系
【分析】利用确定直线的条件、射线的定义、对顶角的性质、三角形的三边关系分别判断后即可确定正确的选项.
①两点确定一条直线,正确;
②射线OA和射线AO不是同一条射线,错误;
③对顶角相等,正确;
④三角形任意两边和大于第三边的理由是两点之间线段最短,正确,
故填①③④.
【点评】本题考查了确定直线的条件、射线的定义、对顶角的性质、三角形的三边关系,属于基础知识,比较简单.
【考点】角平分线的性质.
【分析】如图,作辅助线;首先运用角平分线的性质证明CD=DE;其次求出DE的长度,即可解决问题.
解:如图,过点D作DE⊥AB于点E;
∵∠C=90°,AD平分∠BAC,
∴CD=DE;
∵,且AB=10,
∴DE=3,CD=DE=3.
故答案为3.
【点评】该题主要考查了角平分线的性质、三角形的面积公式等几何知识点及其应用问题;解题的关键是作辅助线.
【考点】等腰三角形的性质;三角形三边关系.
【分析】分腰长为8和10两种情况,可求得三角形的三边,再利用三角形的三边关系进行验证,可求得其周长.
解:当腰长为8时,则三角形的三边长分别为8、8、10,满足三角形的三边关系,此时周长为26;
当腰长为10时,则三角形的三边长分别为10、10、8,满足三角形的三边关系,此时周长为28;
综上可知三角形的周长为26或28,
故答案为:26或28.
【点评】本题主要考查等腰三角形的性质,掌握等腰三角形的两腰相等是解题的关键,注意利用三角形的三边关系进行验证.
【考点】负整数指数幂.
【分析】根据幂的负整数指数运算法则计算.
解:原式==.
故答案为:.
【点评】本题考查的是幂的负整数指数运算,先把底数化成其倒数,然后将负整数指数幂当成正的进行计算.
【考点】一元一次不等式的整数解.
【分析】先解不等式,求出其解集,再根据解集判断其正整数解.
解:2x+9≥3(x+2),
去括号得,2x+9≥3x+6,
移项得,2x﹣3x≥6﹣9,
合并同类项得,﹣x≥﹣3,
系数化为1得,x≤3,
故其正整数解为1,2,3.
故答案为:1,2,3.
【点评】本题考查了一元一次不等式的整数解,会解不等式是解题的关键.
【考点】平方差公式,零指数幂,负整数指数幂,二次根式的化简求值
【分析】利用负整数指数幂和零指数幂求出a的值,利用平方差公式,求出b的值,进而即可求解.
解:∵,,
∴,
故答案是:2.
【点评】本题主要考查二次根式求值,熟练掌握负整数指数幂和零指数幂以及平方差公式,是解题的关键.
【考点】三角形内角和定理;等腰三角形的性质
【分析】先判断出∠AEC=90°,进而求出∠ADC=∠C=74°,最后用等腰三角形的外角等于底角的2倍即可得出结论.
解:∵AD=AC,点E是CD中点,
∴AE⊥CD,
∴∠AEC=90°,
∴∠C=90°﹣∠CAE=74°,
∵AD=AC,
∴∠ADC=∠C=74°,
∵AD=BD,
∴2∠B=∠ADC=74°,
∴∠B=37°,
故答案为37°.
【点评】此题主要考查了等腰三角形的性质,直角三角形的性质,三角形外角的性质,求出∠AC=74°是解本题的关键.
1 、解答题
【考点】分式的乘除法.
【分析】根据分式的乘法,可得答案.
解:原式= =.
【点评】这类题主要考查分式的化简,注意约分
【考点】解一元一次不等式组
【分析】分别解每一个不等式,然后即可得出解集.
解:
解不等式①得:,
解不等式②得:,
∴此不等式组的解集为.
【点评】本题考查了解一元一次不等式组,掌握不等式的解法是解题关键.
【考点】二次根式的混合运算,解二元一次方程组
【分析】(1)根据二次根式的运算法则即可求解;
(2)根据加减消元法即可求解.
解:(1)①
=
=
=3-5
=-2
②
=
=
(2)解
①×2得4x-2y=-8③
③-②得3y=15
解得y=5
把y=5代入①得2x-5=-4
解得x=
∴原方程组的解为.
【点评】此题主要考查二次根式与方程组的求解,解题的关键是熟知其运算法则.
【考点】分式方程的应用
【分析】设甲工程队每天整治河道xm,则乙工程队每天整治(1500-x)m,根据“甲工程队整治3600米所用的时间与乙工程队整治2400米所用时间相等”列方程进行求解即可.
解:设甲工程队每天整治河道xm,则乙工程队每天整治(1500-x)m,
由题意得:,
解得:x=900,
经检验的x=900是原方程的根且符合实际意义,
答:甲工程队每天整治河道900米.
【点睛】本题考查了分式方程的应用,弄清题意,找准等量关系列出方程是解题的关键.注意分式方程要进行检验.
【考点】 作图—应用与设计作图.
【分析】 (1)直接利用等腰三角形的性质结合三角形的面积求法得出即可;
(2)直接利用等腰三角形的性质结合直角三角形的性质得出即可.
解:(1)如图1所示:△ABC即为所求;
(2)如图2所示:△ABC即为所求.
【点评】 此题主要考查了应用设计与作图,正确利用等腰三角形的性质得出是解题关键.
【考点】三角形的内角和,全等三角形的判定与性质
【分析】(1)根据题意证明△ACE≌△BCD即可求解;
(2)根据三角形的内角和及全等三角形的性质即可得到的度数.
解:(1)∵,,
∴∠ACB=∠ECD=90°
∴∠ACB+∠BCE=∠ECD+∠BCE
即∠ACE=∠BCD
又.
∴△ACE≌△BCD
∴
(2)∵△ACE≌△BCD
∴∠A=∠B
设AE与BC交于O点,
∴∠AOC=∠BOF
∴∠A+∠AOC+∠ACO=∠B+∠BOF+∠BFO=180°
∴∠BFO=∠ACO=90°
故=180°-∠BFO=90°.
【点评】此题主要考查全等三角形的判定与性质,解题的关键是熟知全等三角形的判定定理.
【考点】二元一次方程组的应用;一元一次不等式的应用
【分析】(1)设购买一个篮球需x元,购买一个足球需y元,根据题意列出方程组解答即可;
(2)设购买a个篮球,根据题意列出不等式解答即可.
解:(1)设购买一个篮球需x元,购买一个足球需y元,根据题意可得:
,
解得:,
答:购买一个篮球,一个足球各需150元,100元;
(2)设购买a个篮球,根据题意可得:0.9×150a+0.85×100(10﹣a)≤1050,
解得:a≤4,
答;最多可购买4个篮球.
【点评】本题考查二元一次方程组的应用、一元一次不等式的应用,关键是根据数量作为等量关系列出方程,根据总费用作为不等关系列出不等式求解.
【考点】解分式方程,等边三角形性质,全等三角形的性质和判定
【分析】(1)先求出方程的解为,即可求解;
(2)由“SAS”可证△CAO≌△DAB,可得∠DBA=∠COA=90°,由四边形内角和定理可求解;
(3)由“SAS”可证△ABG≌△OBF可得OF=AG,∠BAG=∠BOF=60°,可求∠OAH=60°,可得AH=6,即可求解.
解:(1)∵是方程的解.
解得:,
检验当时,,,
∴是原方程的解,
∴点;
(2)∵△ACD,△ABO是等边三角形,
∴AO=AB,AD=AC,∠BAO=∠CAD=60°,
∴∠CAO=∠BAD,且AO=AB,AD=AC,
∴△CAO≌△DAB(SAS)
∴∠DBA=∠COA=90°,
∴∠ABE=90°,
∵∠AOE+∠ABE+∠OAB+∠BEO=360°,
∴∠BEO=120°;
(3)GH AF的值是定值,
理由如下:∵△ABC,△BFG是等边三角形,
∴BO=AB=AO=3,FB=BG,∠BOA=∠ABO=∠FBG=60°,
∴∠OBF=∠ABG,且OB=AB,BF=BG,
∴△ABG≌△OBF(SAS),
∴OF=AG,∠BAG=∠BOF=60°,
∴AG=OF=OA+AF=3+AF,
∵∠OAH=180° ∠OAB ∠BAG,
∴∠OAH=60°,且∠AOH=90°,OA=3,
∴AH=6,
∴GH AF=AH+AG AF=6+3+AF AF=9.
【点评】本题是三角形综合题,考查了分式方程的解法,等边三角形性质,全等三角形的性质和判定的应用,主要考查学生运用定理进行推理的能力.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
湘教版八年级2021-2022期末模拟练习3
姓名:__________班级:__________考号:__________总分__________
1 、选择题(本大题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
(2021年湖南省常德市)若,下列不等式不一定成立的是( )
A. B. C. D.
(2021年辽宁省盘锦市)下列运算正确的是( )
A. B. C. D.
对于任意三角形的高,下列说法不正确的是( )
A. 锐角三角形有三条高
B. 直角三角形只有一条高
C. 任意三角形都有三条高
D. 钝角三角形有两条高在三角形的外部
下列说法正确的是( )
A.两边和一角对应相等的两个三角形全等
B.面积相等的两三角形全等
C.有一边相等的两个等腰直角三角形全等
D.有两角和一边对应相等的两个三角形全等
估计+1的值( )
A.在1和2之间 B.在2和3之间 C.在3和4之间 D.在4和5之间
(2019年湖北省荆门市)﹣的倒数的平方是( )
A.2 B. C.﹣2 D.﹣
如图,已知∠CAB=∠DAB,则下列不能判定△ABC≌△ABD的条件是( )
A. ∠C=∠D B. AC=AD C. ∠CBA=∠DBA D. BC=BD
(2018年湖南省张家界市)若关于x的分式方程=1的解为x=2,则m的值为( )
A.5 B.4 C.3 D.2
(2021年海南省)如图,已知,直线与直线分别交于点,分别以点为圆心,大于的长为半径画弧,两弧相交于点,作直线,交直线b于点C,连接,若,则的度数是( )
A. B. C. D.
如图,直角坐标系中,点A(﹣2,2)、B(0,1)点P在x轴上,且△PAB是等腰三角形,则满足条件的点P共有( )个.
A. 1 B. 2 C. 3 D. 4
1 、填空题(本大题共8小题,每小题3分,共24分)
(2017年浙江省宁波市试卷)实数﹣8的立方根是 .
下列说法:①两点确定一条直线;②射线OA和射线AO是同一条射线;③对顶角相等;④三角形任意两边和大于第三边的理由是两点之间线段最短.正确的序号是________.
如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为__________________________.
若等腰三角形两边长分别为8,10,则这个三角形的周长为 .
(2017年四川省乐山市 )3﹣2= .
不等式2x+9≥3(x+2)的正整数解是 .
(2021年湖北省荆州市)已知:,,则_____________.
(2018年贵州省遵义市)如图,△ABC中.点D在BC边上,BD=AD=AC,E为CD的中点.若∠CAE=16°,则∠B为 度.
1 、解答题(本大题共8小题,共66分)
(2017年江苏连云港市)化简: .
(2020年北京市)解不等式组:
(1)计算:①;②
(2)解方程组:
(2019年江苏省扬州)“绿水青山就是金山银山”,为了进一步优化河道环境,甲乙两工程队承担河道整治任务,甲、乙两个工程队每天共整治河道1500米,甲工程队整治3600米所用的时间与乙工程队整治2400米所用时间相等。甲工程队每天整治河道多少米?
如图方格纸中每个小正方形的边长均为1,点A,B在小正方形的顶点上.
(1)在图1中画出等腰钝角△ABC(点C在小正方形的顶点上),使△ABC的面积为2;
(2)在图2中画出等腰直角△ABC(点C在小正方形的顶点上),使∠ABC=90°.
(2020年江苏省徐州市)如图,,,.,与交于点.
(1)求证:;
(2)求的度数.
(2018年辽宁省阜新市)在运动会前夕,育红中学都会购买篮球、足球作为奖品.若购买10个篮球和15个足球共花费3000元,且购买一个篮球比购买一个足球多花50元.
(1)求购买一个篮球,一个足球各需多少元?
(2)今年学校计划购买这种篮球和足球共10个,恰逢商场在搞促销活动,篮球打九折,足球打八五折,若此次购买两种球的总费用不超过1050元,则最多可购买多少个篮球?
已知点A在x轴正半轴上,以OA为边作等边OAB,A(x,0),其中x是方程的解.
(1)求点A的坐标;
(2)如图1,点C在y轴正半轴上,以AC为边在第一象限内作等边ACD,连DB并延长交y轴于点E,求的度数;
(3)如图2,点F为x轴正半轴上一动点,点F在点A的右边,连接FB,以FB为边在第一象限内作等边FBG,连GA并延长交y轴于点H,当点F运动时,的值是否发生变化?若不变,求其值;若变化,求出其变化的范围.
答案解析
1 、选择题
【考点】不等式的性质
【分析】根据不等式的性质逐项进行判断即可得到答案.
解:A.在不等式两边同时减去5,不等式仍然成立,即,故选项A不符合题意;
B. 在不等式两边同时除以-5,不等号方向改变,即,故选项B不符合题意;
C.当c≤0时,不等得到,故选项C符合题意;
D. 在不等式两边同时加上c,不等式仍然成立,即,故选项D不符合题意;
故选:C.
【点评】此题主要考查了不等式的性质运用的,熟练掌握不等式的性质是解答此题的关键.
【考点】合并同项类,负整数指数幂,积的乘方,单项式除以单项式
【分析】利用合并同项类,负整数指数幂的运算法则,积的乘方的法则,单项式除以单项式的法则对各选项进行运算即可.
解:、和不是同类项,不能合并,故不符合题意;
、,故不符合题意;
、,故不符合题意;
、,故符合题意.
故选:.
【点评】本题主要考查合并同类项,积的乘方,负整数指数幂,单项式除以单项式,解答的关键是对合并同类项的法则,积的乘方的法则,负整数指数幂的法则,单项式除以单项式的法则的掌握与运用.
【考点】三角形的角平分线、中线和高.
【分析】 根据三角形的高的概念,通过具体作高,发现:任意一个三角形都有三条高,其中锐角三角形的三条高都在三角形的内部;直角三角形有两条高即三角形的两条直角边,一条在内部;钝角三角形有两条高在三角形的外部,一条在内部,据此解答即可.
解:A.锐角三角形有三条高,说法正确,故本选项不符合题意;
B、直角三角形有三条高,说法错误,故本选项符合题意;
C、任意三角形都有三条高,说法正确,故本选项不符合题意;
D、钝角三角形有两条高在三角形的外部,说法正确,故本选项不符合题意;
故选B.
【点评】本题考查了三角形的高:从三角形的一个顶点向它的对边作垂线,垂足与顶点之间的线段叫做三角形的高,注意不同形状的三角形的高的位置.
【考点】全等三角形的判定.
【分析】从各选项提供的已知进行思考,运用判定方法逐一验证,其中D是能够判定三角形全等的,其它选项是错误的.
解:A.两边和一角对应相等,错误,角的位置不确定,而SSA不能确定;
B、错误,面积相等的两三角形不一定重合,不能确定;
C、可能是一个三角形的直角边等于另一个三角形的斜边,故错误;
D、正确,ASA或AAS都能确定.
故选D.
【点评】本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA.SAS、SSS,直角三角形可用HL定理,但AAA.SSA,无法证明三角形全等.在叙述或运用定理时一定要注意位置对应.
【考点】估算无理数的大小.
【分析】直接利用已知无理数得出的取值范围,进而得出答案.
解:∵2<<3,
∴3<+1<4,
∴+1在在3和4之间.
故选:C.
【点评】此题主要考查了估算无理数大小,正确得出的取值范围是解题关键.
【考点】二次根式的性质,算术平方根,实数的性质
【分析】根据倒数,平方的定义以及二次根式的性质化简即可.
解:﹣的倒数的平方为:.
故选:B.
【点评】本题考查了倒数的定义、平方的定义以及二次根式的性质,是基础题,熟记概念是解题的关键
【考点】 全等三角形的判定.
【分析】根据全等三角形的判定定理(SAS,ASA,AAS,SSS)判断即可.
解:A.∵∠D=∠C,∠DAB=∠CAB,AB=AB,
∴根据AAS能推出△ABC≌△ABD,故本选项错误;
B、∵AD=AC,∠DAB=∠CAB,AB=AB,
∴根据SAS能推出△ABC≌△ABD,故本选项错误;
C、∵∠DAB=∠CAB,AB=AB,∠ABD=∠ABC,
∴根据ASA能推出△ABC≌△ABD,故本选项错误;
D、根据BD=BC,AB=AB,∠DAB=∠CAB不能推出△ABC≌△ABD,故本选项正确;
故选D.
【点评】 本题考查了全等三角形判定定理的应用,注意:全等三角形的判定定理有:SAS,ASA,AAS,SSS.
【考点】分式方程的解
【分析】直接解分式方程进而得出答案.
解:∵关于x的分式方程=1的解为x=2,
∴x=m﹣2=2,
解得:m=4.
故选:B.
【点评】此题主要考查了分式方程的解,正确解方程是解题关键.
【考点】线段垂直平分线的作法及性质,平行线的性质,等腰三角形的性质
【分析】根据题意可得直线是线段AB的垂直平分线,进而可得,利用平行线的性质及等腰三角形中等边对等角,可得,所以可求得.
解:∵已知分别以点为圆心,大于的长为半径画弧,两弧相交于点,作直线,交直线b于点C,连接,
∴直线垂直平分线段AB,
∴,
∵,,
∴,
∴,
∴.
故选:C.
【点评】题目主要考查线段垂直平分线的作法及性质、平行线的性质等,根据题意得出直线垂直平分线段AB是解题关键.
【考点】等腰三角形的判定;坐标与图形性质.
【分析】由AB=AP,可得以A为圆心,AB为半径画圆,交x轴有二点P1(﹣1,0),P2(﹣3,0);
由BP=AB,可得以B为圆心,BA为半径画圆,交x轴有二点P3(﹣2,0),(2,0)不能组成△ABP,
由AP=BP,可得AB的垂直平分线交x轴一点P4(PA=PB).
解:如图,点A(﹣2,2)、B(0,1),
①以A为圆心,AB为半径画圆,交x轴有二点P1(﹣1,0),P2(﹣3,0),此时(AP=AB);
②以B为圆心,BA为半径画圆,交x轴有二点P3(﹣2,0),(2,0)不能组成△ABP,故舍去,此时(BP=AB);
③AB的垂直平分线交x轴一点P4(PA=PB),此时(AP=BP);
设此时P4(x,0),
则(x+2)2+4=x2+1,
解得:x=﹣,
∴P4(﹣,0).
∴符合条件的点有4个.
故选D.
【点评】此题考查了等腰三角形的判定.此题那难度适中,注意掌握数形结合思想与分类讨论思想的应用.
1 、填空题
【考点】立方根.
【分析】利用立方根的定义即可求解.
解:∵(﹣2)3=﹣8,
∴﹣8的立方根是﹣2.
故答案﹣2.
【点评】本题主要考查了立方根的概念.如果一个数x的立方等于a,即x的三次方等于a(x3=a),那么这个数x就叫做a的立方根,也叫做三次方根.
【考点】直线、射线、线段,三角形三边的关系
【分析】利用确定直线的条件、射线的定义、对顶角的性质、三角形的三边关系分别判断后即可确定正确的选项.
①两点确定一条直线,正确;
②射线OA和射线AO不是同一条射线,错误;
③对顶角相等,正确;
④三角形任意两边和大于第三边的理由是两点之间线段最短,正确,
故填①③④.
【点评】本题考查了确定直线的条件、射线的定义、对顶角的性质、三角形的三边关系,属于基础知识,比较简单.
【考点】角平分线的性质.
【分析】如图,作辅助线;首先运用角平分线的性质证明CD=DE;其次求出DE的长度,即可解决问题.
解:如图,过点D作DE⊥AB于点E;
∵∠C=90°,AD平分∠BAC,
∴CD=DE;
∵,且AB=10,
∴DE=3,CD=DE=3.
故答案为3.
【点评】该题主要考查了角平分线的性质、三角形的面积公式等几何知识点及其应用问题;解题的关键是作辅助线.
【考点】等腰三角形的性质;三角形三边关系.
【分析】分腰长为8和10两种情况,可求得三角形的三边,再利用三角形的三边关系进行验证,可求得其周长.
解:当腰长为8时,则三角形的三边长分别为8、8、10,满足三角形的三边关系,此时周长为26;
当腰长为10时,则三角形的三边长分别为10、10、8,满足三角形的三边关系,此时周长为28;
综上可知三角形的周长为26或28,
故答案为:26或28.
【点评】本题主要考查等腰三角形的性质,掌握等腰三角形的两腰相等是解题的关键,注意利用三角形的三边关系进行验证.
【考点】负整数指数幂.
【分析】根据幂的负整数指数运算法则计算.
解:原式==.
故答案为:.
【点评】本题考查的是幂的负整数指数运算,先把底数化成其倒数,然后将负整数指数幂当成正的进行计算.
【考点】一元一次不等式的整数解.
【分析】先解不等式,求出其解集,再根据解集判断其正整数解.
解:2x+9≥3(x+2),
去括号得,2x+9≥3x+6,
移项得,2x﹣3x≥6﹣9,
合并同类项得,﹣x≥﹣3,
系数化为1得,x≤3,
故其正整数解为1,2,3.
故答案为:1,2,3.
【点评】本题考查了一元一次不等式的整数解,会解不等式是解题的关键.
【考点】平方差公式,零指数幂,负整数指数幂,二次根式的化简求值
【分析】利用负整数指数幂和零指数幂求出a的值,利用平方差公式,求出b的值,进而即可求解.
解:∵,,
∴,
故答案是:2.
【点评】本题主要考查二次根式求值,熟练掌握负整数指数幂和零指数幂以及平方差公式,是解题的关键.
【考点】三角形内角和定理;等腰三角形的性质
【分析】先判断出∠AEC=90°,进而求出∠ADC=∠C=74°,最后用等腰三角形的外角等于底角的2倍即可得出结论.
解:∵AD=AC,点E是CD中点,
∴AE⊥CD,
∴∠AEC=90°,
∴∠C=90°﹣∠CAE=74°,
∵AD=AC,
∴∠ADC=∠C=74°,
∵AD=BD,
∴2∠B=∠ADC=74°,
∴∠B=37°,
故答案为37°.
【点评】此题主要考查了等腰三角形的性质,直角三角形的性质,三角形外角的性质,求出∠AC=74°是解本题的关键.
1 、解答题
【考点】分式的乘除法.
【分析】根据分式的乘法,可得答案.
解:原式= =.
【点评】这类题主要考查分式的化简,注意约分
【考点】解一元一次不等式组
【分析】分别解每一个不等式,然后即可得出解集.
解:
解不等式①得:,
解不等式②得:,
∴此不等式组的解集为.
【点评】本题考查了解一元一次不等式组,掌握不等式的解法是解题关键.
【考点】二次根式的混合运算,解二元一次方程组
【分析】(1)根据二次根式的运算法则即可求解;
(2)根据加减消元法即可求解.
解:(1)①
=
=
=3-5
=-2
②
=
=
(2)解
①×2得4x-2y=-8③
③-②得3y=15
解得y=5
把y=5代入①得2x-5=-4
解得x=
∴原方程组的解为.
【点评】此题主要考查二次根式与方程组的求解,解题的关键是熟知其运算法则.
【考点】分式方程的应用
【分析】设甲工程队每天整治河道xm,则乙工程队每天整治(1500-x)m,根据“甲工程队整治3600米所用的时间与乙工程队整治2400米所用时间相等”列方程进行求解即可.
解:设甲工程队每天整治河道xm,则乙工程队每天整治(1500-x)m,
由题意得:,
解得:x=900,
经检验的x=900是原方程的根且符合实际意义,
答:甲工程队每天整治河道900米.
【点睛】本题考查了分式方程的应用,弄清题意,找准等量关系列出方程是解题的关键.注意分式方程要进行检验.
【考点】 作图—应用与设计作图.
【分析】 (1)直接利用等腰三角形的性质结合三角形的面积求法得出即可;
(2)直接利用等腰三角形的性质结合直角三角形的性质得出即可.
解:(1)如图1所示:△ABC即为所求;
(2)如图2所示:△ABC即为所求.
【点评】 此题主要考查了应用设计与作图,正确利用等腰三角形的性质得出是解题关键.
【考点】三角形的内角和,全等三角形的判定与性质
【分析】(1)根据题意证明△ACE≌△BCD即可求解;
(2)根据三角形的内角和及全等三角形的性质即可得到的度数.
解:(1)∵,,
∴∠ACB=∠ECD=90°
∴∠ACB+∠BCE=∠ECD+∠BCE
即∠ACE=∠BCD
又.
∴△ACE≌△BCD
∴
(2)∵△ACE≌△BCD
∴∠A=∠B
设AE与BC交于O点,
∴∠AOC=∠BOF
∴∠A+∠AOC+∠ACO=∠B+∠BOF+∠BFO=180°
∴∠BFO=∠ACO=90°
故=180°-∠BFO=90°.
【点评】此题主要考查全等三角形的判定与性质,解题的关键是熟知全等三角形的判定定理.
【考点】二元一次方程组的应用;一元一次不等式的应用
【分析】(1)设购买一个篮球需x元,购买一个足球需y元,根据题意列出方程组解答即可;
(2)设购买a个篮球,根据题意列出不等式解答即可.
解:(1)设购买一个篮球需x元,购买一个足球需y元,根据题意可得:
,
解得:,
答:购买一个篮球,一个足球各需150元,100元;
(2)设购买a个篮球,根据题意可得:0.9×150a+0.85×100(10﹣a)≤1050,
解得:a≤4,
答;最多可购买4个篮球.
【点评】本题考查二元一次方程组的应用、一元一次不等式的应用,关键是根据数量作为等量关系列出方程,根据总费用作为不等关系列出不等式求解.
【考点】解分式方程,等边三角形性质,全等三角形的性质和判定
【分析】(1)先求出方程的解为,即可求解;
(2)由“SAS”可证△CAO≌△DAB,可得∠DBA=∠COA=90°,由四边形内角和定理可求解;
(3)由“SAS”可证△ABG≌△OBF可得OF=AG,∠BAG=∠BOF=60°,可求∠OAH=60°,可得AH=6,即可求解.
解:(1)∵是方程的解.
解得:,
检验当时,,,
∴是原方程的解,
∴点;
(2)∵△ACD,△ABO是等边三角形,
∴AO=AB,AD=AC,∠BAO=∠CAD=60°,
∴∠CAO=∠BAD,且AO=AB,AD=AC,
∴△CAO≌△DAB(SAS)
∴∠DBA=∠COA=90°,
∴∠ABE=90°,
∵∠AOE+∠ABE+∠OAB+∠BEO=360°,
∴∠BEO=120°;
(3)GH AF的值是定值,
理由如下:∵△ABC,△BFG是等边三角形,
∴BO=AB=AO=3,FB=BG,∠BOA=∠ABO=∠FBG=60°,
∴∠OBF=∠ABG,且OB=AB,BF=BG,
∴△ABG≌△OBF(SAS),
∴OF=AG,∠BAG=∠BOF=60°,
∴AG=OF=OA+AF=3+AF,
∵∠OAH=180° ∠OAB ∠BAG,
∴∠OAH=60°,且∠AOH=90°,OA=3,
∴AH=6,
∴GH AF=AH+AG AF=6+3+AF AF=9.
【点评】本题是三角形综合题,考查了分式方程的解法,等边三角形性质,全等三角形的性质和判定的应用,主要考查学生运用定理进行推理的能力.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
