人教版初中数学九年级上册25.3.1用频率估计概率 课件 (共19张PPT)
文档属性
| 名称 | 人教版初中数学九年级上册25.3.1用频率估计概率 课件 (共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
25.3用频率估计概率(第一课时)
引出新知
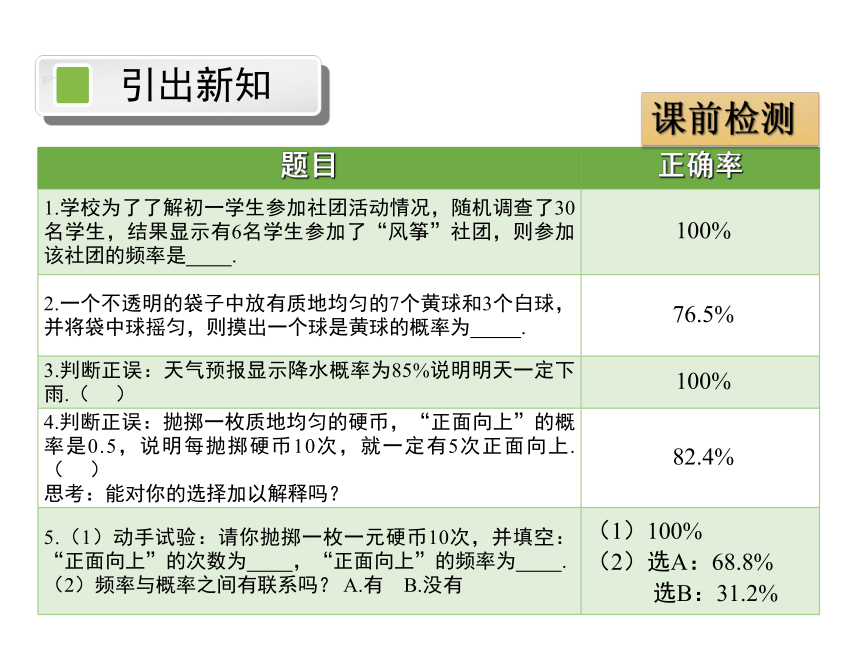
题目 正确率
1.学校为了了解初一学生参加社团活动情况,随机调查了30名学生,结果显示有6名学生参加了“风筝”社团,则参加该社团的频率是 . 100%
2.一个不透明的袋子中放有质地均匀的7个黄球和3个白球,并将袋中球摇匀,则摸出一个球是黄球的概率为 . 76.5%
3.判断正误:天气预报显示降水概率为85%说明明天一定下雨.( ) 100%
4.判断正误:抛掷一枚质地均匀的硬币,“正面向上”的概率是0.5,说明每抛掷硬币10次,就一定有5次正面向上.( )
思考:能对你的选择加以解释吗? 82.4%
5.(1)动手试验:请你抛掷一枚一元硬币10次,并填空:“正面向上”的次数为 ,“正面向上”的频率为 .
(2)频率与概率之间有联系吗? A.有 B.没有 (1)100%
(2)选A:68.8%
选B:31.2%
课前检测
形成认知
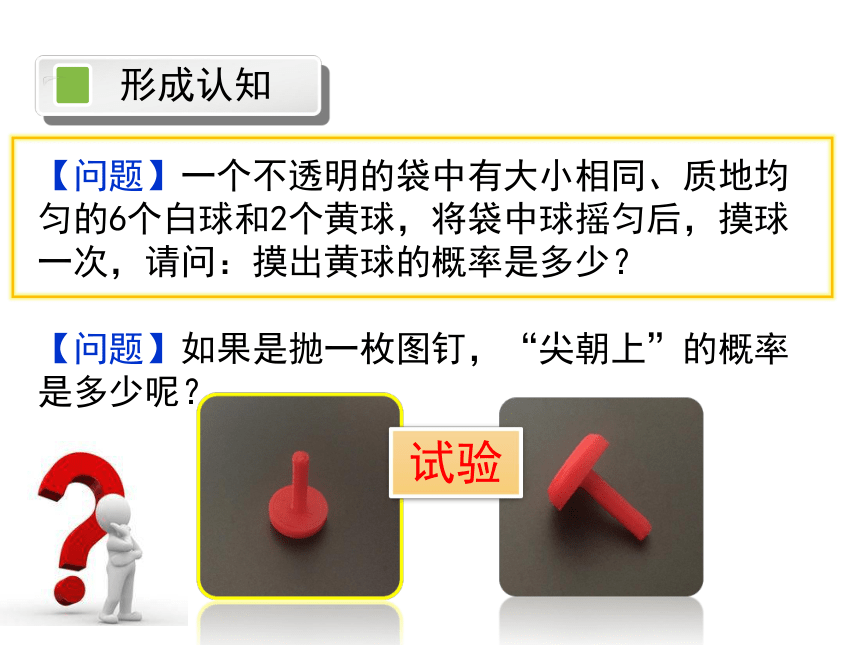
【问题】一个不透明的袋中有大小相同、质地均匀的6个白球和2个黄球,将袋中球摇匀后,摸球一次,请问:摸出黄球的概率是多少?
【问题】如果是抛一枚图钉,“尖朝上”的概率是多少呢?
试验
【活动一】摸球试验
【活动任务】
每两位同学一组,一次摸一个球,观察颜色,记录并放回,摇匀后再摸下一次,完成50次试验.
【活动要求】
分工合作,将试验数据记录在活动记录表中,并拍照上传到作品库.
形成认知
试验条件相同
【问题】各组在相同条件下做的试验,为什么摸出黄球的频率不同?
【总结】每次试验结果都是不确定的,即使再做50次试验,试验结果与前50次试验也不一定相同.
所以频率具有随机性.
形成认知
【问题】为什么试验所得出的频率与摸出黄球的概率不同?
接下来该做什么呢?
掷硬币试验历史数据:
【问题】通过以上活动,你有什么体会?
【总结】
虽然频率具有随机性,但在大量重复试验下,随着试验次数增多,频率会越来越稳定在概率附近.
所以频率具有规律性.
用频率可以估计概率.
形成认知
【反思】频率与概率之间有没有联系?频率与概率一样吗 说说你的看法.
【总结】
频率是试验数据,具有不确定性,受试验影响;
概率是确定的,随机事件的概率本身存在,不随试验次数变化;
在大量重复试验下,频率可以作为概率一个很好的估计.
形成认知
【解决问题】抛一枚“图钉”,“尖朝上”概率是多少?
发展认知
用频率估计概率
【猜一猜】“尖朝上”的可能性大还是“尖落在桌面上”的可能性大?
“尖朝上”的概率大约是多少?
【活动二】抛“图钉”试验
【活动任务】
借助从摸球试验中获得的经验,估计在相同条件下,抛一枚“图钉”,“尖朝上”的概率是多少?
【活动要求】
1.保证试验条件基本相同;
2.根据活动记录表上的要求记录试验数据;
3.整理试验数据,输入Excel中,并提交.
发展认知
发展认知
【反思】通过这个试验,你又有哪些体会?
应用“用频率估计概率”的方法时,前提条件是什么?
【总结】
“用频率估计概率”的方法更具一般性;
在应用时要注意“同等条件下的大量重复试验”这个条件.
1、某射手进行射击,结果如下表所示:
射击次数n 20 100 200 500 800
击中靶心次数m
13
58
104
255
404
击中靶心频率m/n
(1)这个射手射击一次,击中靶心的概率是多少?
0.5
(2)这射手射击1600次,击中靶心的次数是 。
800
0.65
0.58
0.52
0.51
0.55
小刀试牛
2、一批西装质量抽检情况如下:
抽检件数 200 400 600 800 1000 1200
正品件数 190 390 576 773 967 1160
次品的频率
(1)填写表格中次品的频率.
(2)从这批西装中任选一套是次品的概率是多少
(3)若要销售这批西装2000件,为了方便购买次品西装的顾客前来调换,至少应该进多少件西装
2069
小刀试牛
3.如图,小明、小华用4张扑克牌(方块2、黑桃4、黑桃5、梅花5)玩游戏,他俩将扑克牌洗匀后,背面朝上放置在桌面上,小明先抽,小华后抽,抽出的牌不放回。
(1)若小明恰好抽到了黑桃4。
①请在下边框中绘制这种情况的树状图;
②求小华抽出的牌面数字比4大的概率。
(2)小明、小华约定:若小明抽到的牌面数字比小华的大,则小明胜;反之,则小明负。你认为这个游戏是否公平?说明你的理由。
小刀试牛
1.下列事件发生的概率为0的是( )
A、随意掷一枚均匀的硬币两次,至少有一次反面朝上
B、今年冬天黑龙江会下雪
C、随意掷两个均匀的骰子,朝上面的点数之和为1
D、一个转盘被分成6个扇形,按红、白、白、红、红、白排列,转动转盘,指针停在红色区域.
2.某商店举办有奖储蓄活动,购货满100元者发对奖券一张,在10000张奖券中,设特等奖1个,一等奖10个,二等奖100个。若某人购物满100元,那么他中一等奖的概率是( )
A. B. C. D.
C
B
当堂练习
3.一个袋子中装有6个黑球3个白球,这些球除颜色外,形状、大小、质等完全相同.在看不到球的条件下,随机地从这个袋子中摸出一个球,求摸到白球的概率为多少
4.一只口袋中放着若干只红球和白球,这两种球除了颜色以外没有任何其他区别,袋中的球已经搅匀,蒙上眼睛从口袋中取出一只球,取出红球的概率是 .
(1)取出白球的概率是多少?
(2)如果袋中的白球有18只,那么袋中的红球有多少只?
(提示:利用概率的计算公式用方程进行计算.)
当堂练习
课堂小结
1.本节课你学到了什么知识?
2.应用“用频率估计概率”的方法求随机事件发生的概率时,需要注意什么?
3.在本节课学习的过程中,有哪些经验可以为你今后的学习提供帮助?
概率统计在很多领域中具有广泛的应用,比如“遗传学之父”——生物学家孟德尔,利用豌豆实验发现了遗传规律,其中就用到了用频率估计概率.
课堂小结
谢谢同学们的认真参与!
25.3用频率估计概率(第一课时)
引出新知
题目 正确率
1.学校为了了解初一学生参加社团活动情况,随机调查了30名学生,结果显示有6名学生参加了“风筝”社团,则参加该社团的频率是 . 100%
2.一个不透明的袋子中放有质地均匀的7个黄球和3个白球,并将袋中球摇匀,则摸出一个球是黄球的概率为 . 76.5%
3.判断正误:天气预报显示降水概率为85%说明明天一定下雨.( ) 100%
4.判断正误:抛掷一枚质地均匀的硬币,“正面向上”的概率是0.5,说明每抛掷硬币10次,就一定有5次正面向上.( )
思考:能对你的选择加以解释吗? 82.4%
5.(1)动手试验:请你抛掷一枚一元硬币10次,并填空:“正面向上”的次数为 ,“正面向上”的频率为 .
(2)频率与概率之间有联系吗? A.有 B.没有 (1)100%
(2)选A:68.8%
选B:31.2%
课前检测
形成认知
【问题】一个不透明的袋中有大小相同、质地均匀的6个白球和2个黄球,将袋中球摇匀后,摸球一次,请问:摸出黄球的概率是多少?
【问题】如果是抛一枚图钉,“尖朝上”的概率是多少呢?
试验
【活动一】摸球试验
【活动任务】
每两位同学一组,一次摸一个球,观察颜色,记录并放回,摇匀后再摸下一次,完成50次试验.
【活动要求】
分工合作,将试验数据记录在活动记录表中,并拍照上传到作品库.
形成认知
试验条件相同
【问题】各组在相同条件下做的试验,为什么摸出黄球的频率不同?
【总结】每次试验结果都是不确定的,即使再做50次试验,试验结果与前50次试验也不一定相同.
所以频率具有随机性.
形成认知
【问题】为什么试验所得出的频率与摸出黄球的概率不同?
接下来该做什么呢?
掷硬币试验历史数据:
【问题】通过以上活动,你有什么体会?
【总结】
虽然频率具有随机性,但在大量重复试验下,随着试验次数增多,频率会越来越稳定在概率附近.
所以频率具有规律性.
用频率可以估计概率.
形成认知
【反思】频率与概率之间有没有联系?频率与概率一样吗 说说你的看法.
【总结】
频率是试验数据,具有不确定性,受试验影响;
概率是确定的,随机事件的概率本身存在,不随试验次数变化;
在大量重复试验下,频率可以作为概率一个很好的估计.
形成认知
【解决问题】抛一枚“图钉”,“尖朝上”概率是多少?
发展认知
用频率估计概率
【猜一猜】“尖朝上”的可能性大还是“尖落在桌面上”的可能性大?
“尖朝上”的概率大约是多少?
【活动二】抛“图钉”试验
【活动任务】
借助从摸球试验中获得的经验,估计在相同条件下,抛一枚“图钉”,“尖朝上”的概率是多少?
【活动要求】
1.保证试验条件基本相同;
2.根据活动记录表上的要求记录试验数据;
3.整理试验数据,输入Excel中,并提交.
发展认知
发展认知
【反思】通过这个试验,你又有哪些体会?
应用“用频率估计概率”的方法时,前提条件是什么?
【总结】
“用频率估计概率”的方法更具一般性;
在应用时要注意“同等条件下的大量重复试验”这个条件.
1、某射手进行射击,结果如下表所示:
射击次数n 20 100 200 500 800
击中靶心次数m
13
58
104
255
404
击中靶心频率m/n
(1)这个射手射击一次,击中靶心的概率是多少?
0.5
(2)这射手射击1600次,击中靶心的次数是 。
800
0.65
0.58
0.52
0.51
0.55
小刀试牛
2、一批西装质量抽检情况如下:
抽检件数 200 400 600 800 1000 1200
正品件数 190 390 576 773 967 1160
次品的频率
(1)填写表格中次品的频率.
(2)从这批西装中任选一套是次品的概率是多少
(3)若要销售这批西装2000件,为了方便购买次品西装的顾客前来调换,至少应该进多少件西装
2069
小刀试牛
3.如图,小明、小华用4张扑克牌(方块2、黑桃4、黑桃5、梅花5)玩游戏,他俩将扑克牌洗匀后,背面朝上放置在桌面上,小明先抽,小华后抽,抽出的牌不放回。
(1)若小明恰好抽到了黑桃4。
①请在下边框中绘制这种情况的树状图;
②求小华抽出的牌面数字比4大的概率。
(2)小明、小华约定:若小明抽到的牌面数字比小华的大,则小明胜;反之,则小明负。你认为这个游戏是否公平?说明你的理由。
小刀试牛
1.下列事件发生的概率为0的是( )
A、随意掷一枚均匀的硬币两次,至少有一次反面朝上
B、今年冬天黑龙江会下雪
C、随意掷两个均匀的骰子,朝上面的点数之和为1
D、一个转盘被分成6个扇形,按红、白、白、红、红、白排列,转动转盘,指针停在红色区域.
2.某商店举办有奖储蓄活动,购货满100元者发对奖券一张,在10000张奖券中,设特等奖1个,一等奖10个,二等奖100个。若某人购物满100元,那么他中一等奖的概率是( )
A. B. C. D.
C
B
当堂练习
3.一个袋子中装有6个黑球3个白球,这些球除颜色外,形状、大小、质等完全相同.在看不到球的条件下,随机地从这个袋子中摸出一个球,求摸到白球的概率为多少
4.一只口袋中放着若干只红球和白球,这两种球除了颜色以外没有任何其他区别,袋中的球已经搅匀,蒙上眼睛从口袋中取出一只球,取出红球的概率是 .
(1)取出白球的概率是多少?
(2)如果袋中的白球有18只,那么袋中的红球有多少只?
(提示:利用概率的计算公式用方程进行计算.)
当堂练习
课堂小结
1.本节课你学到了什么知识?
2.应用“用频率估计概率”的方法求随机事件发生的概率时,需要注意什么?
3.在本节课学习的过程中,有哪些经验可以为你今后的学习提供帮助?
概率统计在很多领域中具有广泛的应用,比如“遗传学之父”——生物学家孟德尔,利用豌豆实验发现了遗传规律,其中就用到了用频率估计概率.
课堂小结
谢谢同学们的认真参与!
同课章节目录
