2021-2022学年人教版数学七年级上册4.3.2 角的比较与运算 课件(29张)
文档属性
| 名称 | 2021-2022学年人教版数学七年级上册4.3.2 角的比较与运算 课件(29张) |

|
|
| 格式 | zip | ||
| 文件大小 | 922.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 00:00:00 | ||
图片预览





文档简介
(共29张PPT)
人教版 七年级上
4.3.2 角的比较与运算
学习目标
1.通过观察与操作,体会角的大小,会比较角的大小,能估计一个角的大小;
2.在图形中认识角的和、差关系,在操作中认识角的平分线。
知识回顾
1.叙述角的定义.
2. 比较线段长短,有哪些方法呢?
(1).静态:有公共端点的两条射线组成的图形叫做角.
(2).动态:角可以看成是一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形。射线旋转时经过的平面部分叫角的内部。
知识回顾
1.叠合法
2.度量法
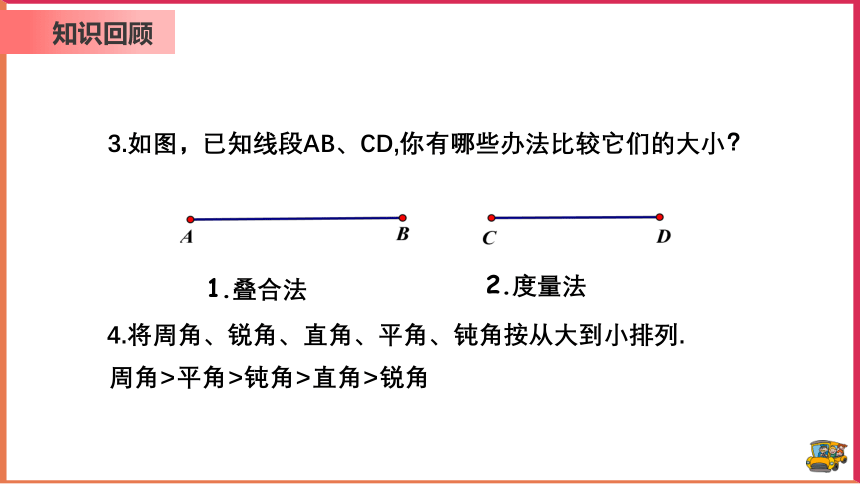
3.如图,已知线段AB、CD,你有哪些办法比较它们的大小?
4.将周角、锐角、直角、平角、钝角按从大到小排列.
周角>平角>钝角>直角>锐角
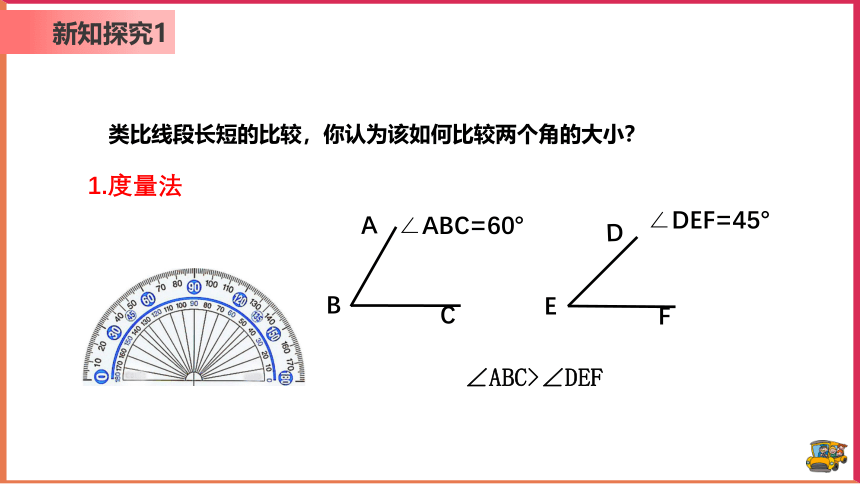
类比线段长短的比较,你认为该如何比较两个角的大小?
新知探究1
B
C
A
E
F
D
∠ABC=60°
∠DEF=45°
∠ABC>∠DEF
1.度量法
新知探究1
1.把量角器放在角的上面;使量角器的中心和角的顶点重合;
2.零度刻度线和角的一条边重合;
3.角的另一条边所对的量角器上的刻度,就是这个角的度数。
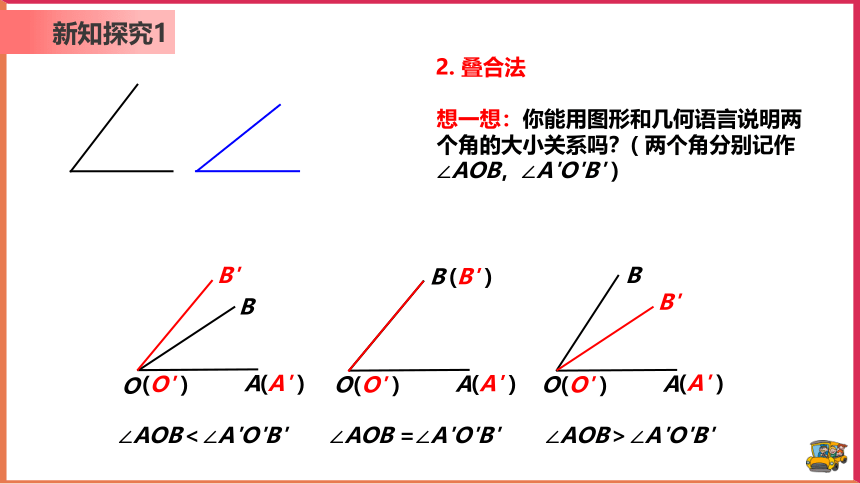
2. 叠合法
A
B
O
(O' )
B'
(A' )
A
B
O
A
B
O
想一想:你能用图形和几何语言说明两个角的大小关系吗?( 两个角分别记作∠AOB,∠A'O'B' )
(O' )
B'
(A' )
∠AOB<∠A'O'B'
∠AOB =∠A'O'B'
∠AOB>∠A'O'B'
(O' )
(B' )
(A' )
新知探究1
思考:图中共有几个角?它们之间有什么关系?
答:有三个角,关系是:
∠AOC是∠AOB与 ∠BOC的和,记作 ∠AOC=∠AOB+∠BOC,
∠AOB是 ∠AOC与 ∠BOC的差,记作 ∠AOB=∠AOC-∠BOC,
∠BOC是 ∠AOC与 ∠AOB的差,记作 ∠BOC=∠AOC-∠AOB.
O
C
B
A
新知探究1
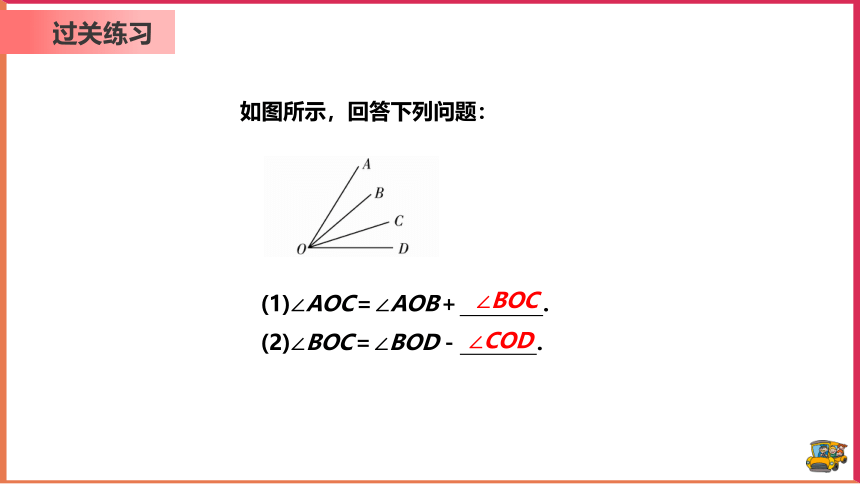
如图所示,回答下列问题:
(1)∠AOC=∠AOB+ .
(2)∠BOC=∠BOD- .
∠BOC
∠COD
过关练习
B
A
O
C
动手做一做:在纸上画∠AOB,然后将其剪下来,将其沿经过顶点的线对折,使边OA与OB重合.将角展开,折痕上任取一点记作点C.类比线段中点的定义,填空:
∠AOC_____∠COB;
∠AOB=_____∠AOC.
=
2
新知探究2
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
O
B
A
C
∵ OC 是∠AOB 的角平分线,
∴ ∠AOC =∠BOC
∠AOB =2∠BOC =2∠AOC.
我们把射线OC叫做∠AOB的角平分线
课堂小结
例1 如图,O 是直线 AB 上一点,∠AOC=53°17′,求∠BOC 的度数.
解:∵∠AOB 是平角,
∠AOB= ∠AOC+∠BOC.
∴∠BOC=∠AOB-∠AOC
=180°-53°17′
=179°60′-53°17′
=126°43′.
O
C
B
A
如何计算?
可以向 180 借
1 ,化为60′.
例题讲解
如图,已知∠AOB=80°,∠AOC=15°,OD是∠AOB的平分线,求∠DOC的度数.
解:因为∠AOB=80°,OD是∠AOB的平分线,
所以∠AOD=∠BOD=40°.
因为∠AOC=15°,
所以∠DOC=∠AOD-∠AOC=40°-15°=25°.
变式训练
例2 把一个周角 7 等分,每一份是多少度的角 (精确到分)?
解:360°÷7 = 51°+3°÷7
= 51°+180′÷7
≈ 51°26′.
答:每份是51°26′的角.
有余数,可以把度的余数化成分后再除
例题讲解
解:设∠BOC=4x°,则∠COD=5x°,∠DOA=6x°,
∠AOB=360°-(4x°+5x°+6x°),
因为∠BOC-∠AOB=20°,
所以4x°-[360°-(4x°+5x°+6x°)]=20°,
解得x=20,所以∠AOB=60°.
如图,∠BOC-∠AOB=20°,∠BOC∶∠COD∶∠DOA=4∶5∶6,求∠AOB的度数.
变式训练
方法总结:涉及到度、分、秒的角度的加与减,要将度与度、分与分、秒与秒分别相加、减,分秒相加时逢60要进位,相减时要借1作60.
变式训练
要点1 角的比较
1. 度量法:用 量出角的度数,根据 大小来比较.
2. 叠合法:把两个角叠合比较,使它们的顶点和一条边 ,另一条边落在 ,根据另一条边的位置进行比较.
要点1 1. 量角器 度数 2. 重合 同侧
课堂小结
要点2 角的平分线
1. 一般地,从一个角的顶点出发,把这个角分成两个 的角的 ,叫做这个角的平分线.角平分线是在角的 从角的顶点引出的一条射线,不是直线或 .
2. 类似角的平分线,从角的顶点引出的射线,将角分成 的n个角,叫做角的n等分线.
要点2 1. 相等 射线 内部 线段 2. 相等
课堂小结
要点3 角的运算
角的运算的实质是求角的和、差、倍、分,这里的加减,要将度与度、分与分、秒与秒相加减,分秒相加时逢 要进位,相减时要借 作60.
要点3 60 1
课堂小结
体验收获
今天我们学习了哪些知识?
1.如果比较两个角的大小?
2.怎样表示角的和与差呢?
3.什么是角的平分线?
达标检测
1.填空:
(1)∠AOC=∠AOB+∠_______;
(2)∠BOD=∠COD+∠_______;
(3)∠AOC=∠AOD-∠_______;
(4)∠BOC=∠______-∠______-∠_____;
(5)∠BOC=∠AOC+∠BOD-∠_______.
BOC
BOC
COD
AOD
AOB
COD
AOD
达标检测
2.已知∠ABC=30°,BD是∠ABC的平分线,则∠ABD=______度.
15
B
达标检测
5. 下列说法错误的是( )
A. 角的大小与角的边的长短没有关系
B. 角的大小与它们的度数大小是一致的
C. 用叠合法比较两个角的大小,只要把两个角的顶点和任意一边重合即可
D. 用度量法比较两个角的大小,只要把两个角的度数量出,比较度数的大小即可
C
达标检测
6. 如图所示,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是( )
A. 20° B. 25° C. 30° D. 70°
D
达标检测
7. 如图所示,若∠AOB=∠COD,那么( )
A. ∠1>∠2 B. ∠1<∠2
C. ∠1=∠2 D. ∠1,∠2大小不定
C
达标检测
解:由OD平分∠AOC,OE平分∠BOC,
可知∠1=∠2,∠3=∠4,
∠AOB=∠1+∠2+∠3+∠4=2∠2+2∠3=2(∠2+∠3)=2∠DOE=2×90°=180°,
所以A,O,B在同一条直线上.
8. 如图所示,OD平分∠AOC,OE平分∠BOC,且∠DOE=90°,试说明:A,O,B三点在同一条直线上.
达标检测
9. 如图,∠BOC-∠AOB=20°,∠BOC∶∠COD∶∠DOA=4∶5∶6,求∠AOB的度数.
解:设∠BOC=4x°,
则∠COD=5x°,∠DOA=6x°,∠AOB=360°-(4x°+5x°+6x°),
因为∠BOC-∠AOB=20°,
所以4x°-[360°-(4x°+5x°+6x°)]=20°,
解得x=20,所以∠AOB=60°.
达标检测
作业布置
教材练习题1-3题
人教版 七年级上
4.3.2 角的比较与运算
学习目标
1.通过观察与操作,体会角的大小,会比较角的大小,能估计一个角的大小;
2.在图形中认识角的和、差关系,在操作中认识角的平分线。
知识回顾
1.叙述角的定义.
2. 比较线段长短,有哪些方法呢?
(1).静态:有公共端点的两条射线组成的图形叫做角.
(2).动态:角可以看成是一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形。射线旋转时经过的平面部分叫角的内部。
知识回顾
1.叠合法
2.度量法
3.如图,已知线段AB、CD,你有哪些办法比较它们的大小?
4.将周角、锐角、直角、平角、钝角按从大到小排列.
周角>平角>钝角>直角>锐角
类比线段长短的比较,你认为该如何比较两个角的大小?
新知探究1
B
C
A
E
F
D
∠ABC=60°
∠DEF=45°
∠ABC>∠DEF
1.度量法
新知探究1
1.把量角器放在角的上面;使量角器的中心和角的顶点重合;
2.零度刻度线和角的一条边重合;
3.角的另一条边所对的量角器上的刻度,就是这个角的度数。
2. 叠合法
A
B
O
(O' )
B'
(A' )
A
B
O
A
B
O
想一想:你能用图形和几何语言说明两个角的大小关系吗?( 两个角分别记作∠AOB,∠A'O'B' )
(O' )
B'
(A' )
∠AOB<∠A'O'B'
∠AOB =∠A'O'B'
∠AOB>∠A'O'B'
(O' )
(B' )
(A' )
新知探究1
思考:图中共有几个角?它们之间有什么关系?
答:有三个角,关系是:
∠AOC是∠AOB与 ∠BOC的和,记作 ∠AOC=∠AOB+∠BOC,
∠AOB是 ∠AOC与 ∠BOC的差,记作 ∠AOB=∠AOC-∠BOC,
∠BOC是 ∠AOC与 ∠AOB的差,记作 ∠BOC=∠AOC-∠AOB.
O
C
B
A
新知探究1
如图所示,回答下列问题:
(1)∠AOC=∠AOB+ .
(2)∠BOC=∠BOD- .
∠BOC
∠COD
过关练习
B
A
O
C
动手做一做:在纸上画∠AOB,然后将其剪下来,将其沿经过顶点的线对折,使边OA与OB重合.将角展开,折痕上任取一点记作点C.类比线段中点的定义,填空:
∠AOC_____∠COB;
∠AOB=_____∠AOC.
=
2
新知探究2
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
O
B
A
C
∵ OC 是∠AOB 的角平分线,
∴ ∠AOC =∠BOC
∠AOB =2∠BOC =2∠AOC.
我们把射线OC叫做∠AOB的角平分线
课堂小结
例1 如图,O 是直线 AB 上一点,∠AOC=53°17′,求∠BOC 的度数.
解:∵∠AOB 是平角,
∠AOB= ∠AOC+∠BOC.
∴∠BOC=∠AOB-∠AOC
=180°-53°17′
=179°60′-53°17′
=126°43′.
O
C
B
A
如何计算?
可以向 180 借
1 ,化为60′.
例题讲解
如图,已知∠AOB=80°,∠AOC=15°,OD是∠AOB的平分线,求∠DOC的度数.
解:因为∠AOB=80°,OD是∠AOB的平分线,
所以∠AOD=∠BOD=40°.
因为∠AOC=15°,
所以∠DOC=∠AOD-∠AOC=40°-15°=25°.
变式训练
例2 把一个周角 7 等分,每一份是多少度的角 (精确到分)?
解:360°÷7 = 51°+3°÷7
= 51°+180′÷7
≈ 51°26′.
答:每份是51°26′的角.
有余数,可以把度的余数化成分后再除
例题讲解
解:设∠BOC=4x°,则∠COD=5x°,∠DOA=6x°,
∠AOB=360°-(4x°+5x°+6x°),
因为∠BOC-∠AOB=20°,
所以4x°-[360°-(4x°+5x°+6x°)]=20°,
解得x=20,所以∠AOB=60°.
如图,∠BOC-∠AOB=20°,∠BOC∶∠COD∶∠DOA=4∶5∶6,求∠AOB的度数.
变式训练
方法总结:涉及到度、分、秒的角度的加与减,要将度与度、分与分、秒与秒分别相加、减,分秒相加时逢60要进位,相减时要借1作60.
变式训练
要点1 角的比较
1. 度量法:用 量出角的度数,根据 大小来比较.
2. 叠合法:把两个角叠合比较,使它们的顶点和一条边 ,另一条边落在 ,根据另一条边的位置进行比较.
要点1 1. 量角器 度数 2. 重合 同侧
课堂小结
要点2 角的平分线
1. 一般地,从一个角的顶点出发,把这个角分成两个 的角的 ,叫做这个角的平分线.角平分线是在角的 从角的顶点引出的一条射线,不是直线或 .
2. 类似角的平分线,从角的顶点引出的射线,将角分成 的n个角,叫做角的n等分线.
要点2 1. 相等 射线 内部 线段 2. 相等
课堂小结
要点3 角的运算
角的运算的实质是求角的和、差、倍、分,这里的加减,要将度与度、分与分、秒与秒相加减,分秒相加时逢 要进位,相减时要借 作60.
要点3 60 1
课堂小结
体验收获
今天我们学习了哪些知识?
1.如果比较两个角的大小?
2.怎样表示角的和与差呢?
3.什么是角的平分线?
达标检测
1.填空:
(1)∠AOC=∠AOB+∠_______;
(2)∠BOD=∠COD+∠_______;
(3)∠AOC=∠AOD-∠_______;
(4)∠BOC=∠______-∠______-∠_____;
(5)∠BOC=∠AOC+∠BOD-∠_______.
BOC
BOC
COD
AOD
AOB
COD
AOD
达标检测
2.已知∠ABC=30°,BD是∠ABC的平分线,则∠ABD=______度.
15
B
达标检测
5. 下列说法错误的是( )
A. 角的大小与角的边的长短没有关系
B. 角的大小与它们的度数大小是一致的
C. 用叠合法比较两个角的大小,只要把两个角的顶点和任意一边重合即可
D. 用度量法比较两个角的大小,只要把两个角的度数量出,比较度数的大小即可
C
达标检测
6. 如图所示,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是( )
A. 20° B. 25° C. 30° D. 70°
D
达标检测
7. 如图所示,若∠AOB=∠COD,那么( )
A. ∠1>∠2 B. ∠1<∠2
C. ∠1=∠2 D. ∠1,∠2大小不定
C
达标检测
解:由OD平分∠AOC,OE平分∠BOC,
可知∠1=∠2,∠3=∠4,
∠AOB=∠1+∠2+∠3+∠4=2∠2+2∠3=2(∠2+∠3)=2∠DOE=2×90°=180°,
所以A,O,B在同一条直线上.
8. 如图所示,OD平分∠AOC,OE平分∠BOC,且∠DOE=90°,试说明:A,O,B三点在同一条直线上.
达标检测
9. 如图,∠BOC-∠AOB=20°,∠BOC∶∠COD∶∠DOA=4∶5∶6,求∠AOB的度数.
解:设∠BOC=4x°,
则∠COD=5x°,∠DOA=6x°,∠AOB=360°-(4x°+5x°+6x°),
因为∠BOC-∠AOB=20°,
所以4x°-[360°-(4x°+5x°+6x°)]=20°,
解得x=20,所以∠AOB=60°.
达标检测
作业布置
教材练习题1-3题
