2021-2022学年人教版数学七年级上册3.4.4 解一元一次方程----分段计费功能问题 课件(29张)
文档属性
| 名称 | 2021-2022学年人教版数学七年级上册3.4.4 解一元一次方程----分段计费功能问题 课件(29张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 00:00:00 | ||
图片预览





文档简介
(共29张PPT)
人教版 七年级上
3.4.2 解一元一次方程
-分段计费功能
学习目标
1.理解分段计费问题的原理,分清有关数量关系,能正确找出实际问题中蕴含的等量关系;
2.培养运用一元一次方程解决实际问题的能力;
3.体会分类思想和方程建模思想,增强应用意识和应用能力。
情境引入
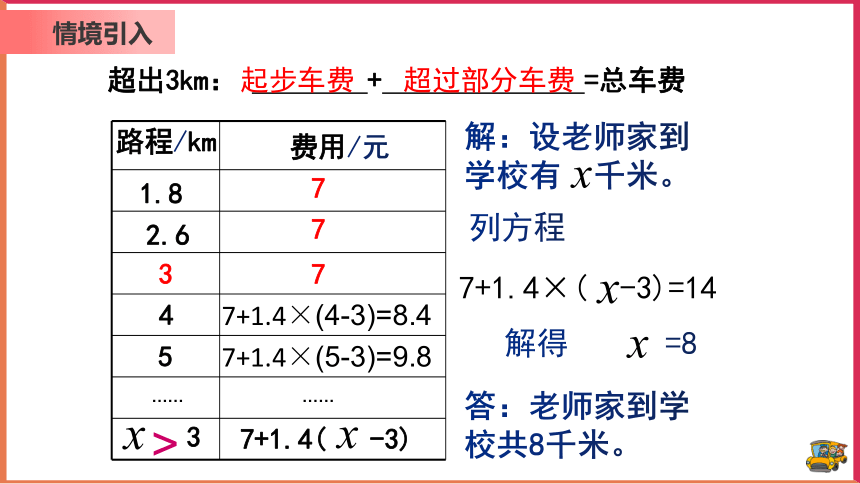
哈密市出租车收费标准:行程不超过3千米,收起步价7元;超过部分每千米路程收费1.4元.(不足1千米按1千米计算)
老师下车时共付车费14元,问老师家到学校的距离?
情境引入
7
7
7
……
……
4
3
2.6
1.8
路程/km
费用/元
7+1.4×(4-3)=8.4
7+1.4( -3)
7+1.4×(5-3)=9.8
解:设老师家到学校有 千米。
列方程
7+1.4×( -3)=14
5
解得 =8
答:老师家到学校共8千米。
超出3km: + =总车费
起步车费
超过部分车费
>
3
分析下图中展示的通讯公司的通信套餐,小组讨论每一种套餐的优惠情况。
新知导入
下表给出的是两种移动电话的计费方式:
月使用费固定收
主叫不超限定时间不再收费
主叫超时,超时部分加收超时费
被叫免费
……
你能从表格中得到哪些信息呢?
新知讲解
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费/(元/分)
主叫限定时间/分
月使用
费/元
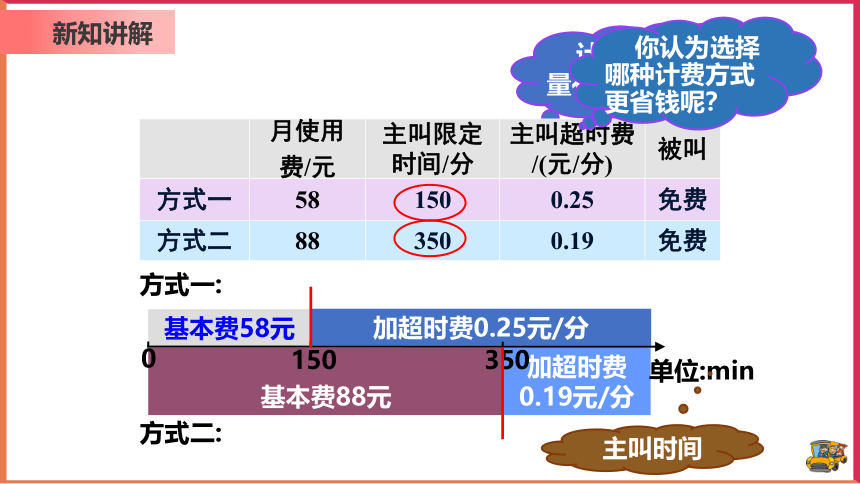
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
0
150
350
单位:min
方式一:
方式二:
计费与什么量有关系呢?
主叫时间
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费/(元/分)
主叫限定时间/分
月使用
费/元
新知讲解
你认为选择哪种计费方式更省钱呢?
设一个月内用移动电话主叫为t min(t是正整数).列表说明:当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
主叫时间t /分 方式一计费/元 方式二计费/元
t <150
t =150
150 < t <350
t =350
t >350
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
0
150
350
单位:min
t
方式一:
方式二:
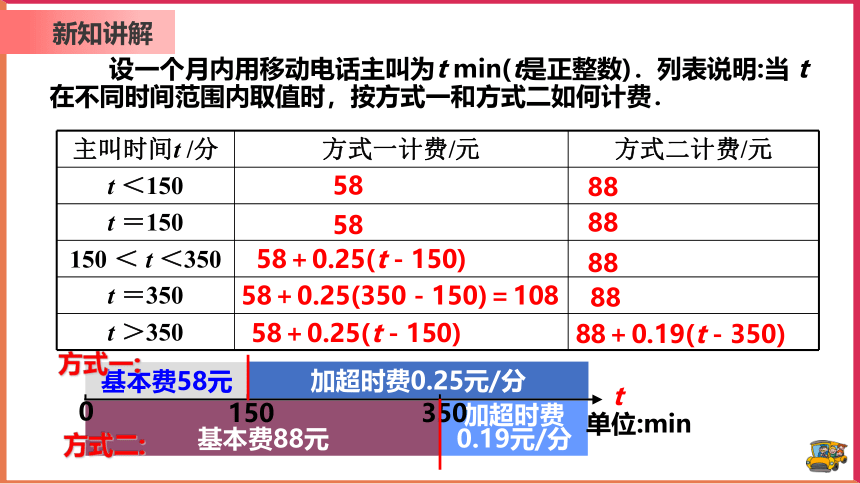
58
58
58+0.25(t-150)
58+0.25(350-150)=108
58+0.25(t-150)
88
88
88
88
88+0.19(t-350)
新知讲解
设一个月内用移动电话主叫为t min(t是正整数).列表说明:当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
主叫时间t /分 方式一计费/元 方式二计费/元
t <150
t =150
150 < t <350
t =350
t >350
58
58
58+0.25(t-150)
58+0.25(350-150)=108
58+0.25(t-150)
88
88
88
88
88+0.19(t-350)
<
省钱
<
省钱
>
省钱
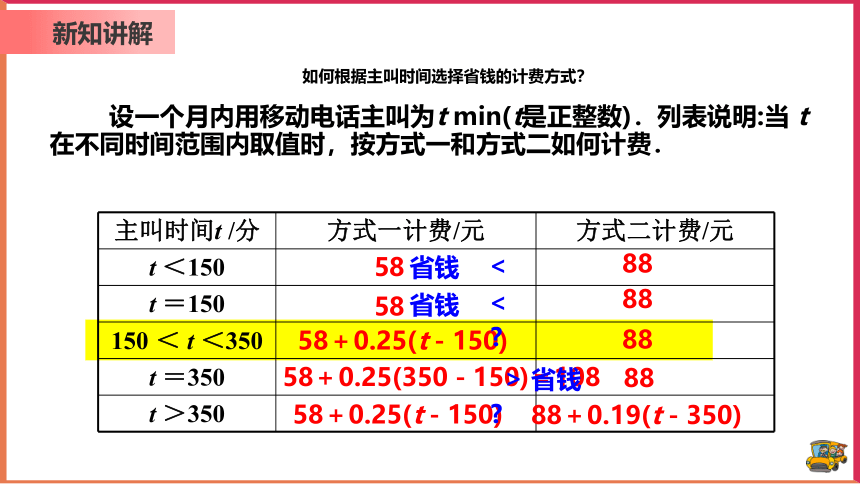
如何根据主叫时间选择省钱的计费方式?
新知讲解
解:令 58+0.25(t-150) =88
解得: t =270
∴当 t =270分时,两种计费方式的费用相等,
当150 < t < 270时,方式一的计费省钱;
和270 < t < 350时,方式二的计费省钱.
主叫时间t /分a 方式一计费/元 方式二计费/元
150 < t <350 58+0.25(t-150) 88
新知讲解
哪种方式省钱呢?
设一个月内用移动电话主叫为t min(t是正整数).列表说明:当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
主叫时间t /分 方式一计费/元 方式二计费/元
t <150
t =150
150 < t <350
t =350
t >350
58
58
58+0.25(t-150)
58+0.25(350-150)=108
58+0.25(t-150)
88
88
88
88
88+0.19(t-350)
<
省钱
<
省钱
>
省钱
新知讲解
如何根据主叫时间选择省钱的计费方式?
解:当t >350时,按方式一的计费为108元加上超出350min部分的超时费0.25(t-350)
按方式二的计费为88元加上超出350min部分的超时费0.19(t-350)
∴按方式二的计费省钱.
主叫时间t /分 方式一计费/元 方式二计费/元
t >350 58+0.25(t-150) 88+0.19(t-350)
新知讲解
哪种方式省钱呢?
综合以上的分析,可以发现:
时,选择方式一省钱;
时,选择方式二省钱.
t <270
t >270
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
单位:min
t
方式一:
方式二:
270
省钱
省钱
相等
新知讲解
分段计费问题解题思路:
1.在用含未知数的式子表示分段计费问题的费用时,要分清在未知数的不同取值范围内费用的不同计算方式,否则易混淆而出错.
2.若已知费用求未知数的值,要注意分类讨论,防止漏解,同时,要对分类讨论求出的未知数的值进行检验,看它是否符合对应的取值范围.
归纳
过关练习
某同学花了30元钱购买图书馆会员证,只限本人使用,凭证购入场券每张1元,不凭证购入场券每张4元,要想使得购会员证比不购会员证合算,该同学去图书馆阅览应超过( )
A.8次 B.9次 C.10次 D.11次
分析:设x次时两种方式花费相同,则
30+x=4x
解得 x=10
C
某校计划购买若干台电脑,现在从两家商场了解到同一型号的电脑每台报价均为4000元,甲商场经理说:“第一台按原报价收费,其余每台优惠25%.”乙商场经理说:“每台优惠20%.”
(1)若购买4台,哪家商场较优惠?买6台呢?
解:(1)购买4台时,
甲商场:4000+(1-0.25)×4000×3=13000(元)
乙商场: (1-0.20) ×4000×4=12800(元)
∴购买4台时,乙商场较优惠;
购买6台时,
甲商场:4000+(1-0.25)×4000×5=19000(元)
乙商场: (1-0.20) ×4000×6=19200(元)
购买6台时,甲商场较优惠.
过关练习
某校计划购买若干台电脑,现在从两家商场了解到同一型号的电脑每台报价均为4000元,甲商场经理说:“第一台按原报价收费,其余每台优惠25%.”乙商场经理说:“每台优惠20%.”
(2)买多少台,两家商场收费一样多?
解:(2)设买x台收费一样,列方程得
4000+0.75×4000(x-1) =0.8×4000x,
解得x=5,
∴买5台收费一样多.
过关练习
某校计划购买若干台电脑,现在从两家商场了解到同一型号的电脑每台报价均为4000元,甲商场经理说:“第一台按原报价收费,其余每台优惠25%.”乙商场经理说:“每台优惠20%.”
(3)你知道怎样选择更省钱吗?
解:(3)当购买数量少于5台时,选乙商场;
当购买数量超过5台时,选甲商场;
当购买数量为5台时,两商场收费一样多,可以从甲、乙两家商场中任选一家.
过关练习
要点 利用一元一次方程解计费问题
解答这类问题的一般步骤:运用一元一次方程解应用题的方法,求解使方案值 的情况;用特殊值试探去选择方案,取 一元一次方程解的值,比较两种方案的优劣后下结论.
相等
小于(或大于)
课堂小结
体验收获
今天我们学习了哪些知识?
1.电话计费问题的核心问题是什么?
2.探究解题的过程大致包含哪几个步骤?
3.我们在探究过程中用到了哪些方法,你有哪些收获?
1. 某电信公司的一种计费标准是:通话时间不超过3分钟,收话费0.2元,以后每分钟收话费0.1元,若小张的话费仅有2.4元,则他能持续通话的最长时间为( )
A. 23分钟 B. 24分钟 C. 25分钟 D. 26分钟
C
达标检测
2.有一旅客带30 kg行李从北京到广州,按民航规定,旅客最多可免费携带20 kg行李,超过部分每千克按飞机票价的1.5%购买行李票.已知该旅客购买的行李票为180元,则他的飞机票价为( )
A.800元 B.1000元 C.1200元 D.1400元
C
达标检测
3. 小明所在城市的“阶梯水价”收费办法是:每户用水不超过5吨,每吨水费x元;超过5吨,超过部分每吨加收2元,小明家今年5月份用水9吨,共交水费为44元,根据题意列出关于x的方程正确的是( )
A. 5x+4(x+2)=44 B. 5x+4(x-2)=44
C. 9(x+2)=44 D. 9(x+2)-4×2=44
A
达标检测
4. 某市居民用电价格改革方案已出台,为鼓励居民节约用电,对居民生活用电实行阶梯价,如下表:
“一户一表”用电量 不超过a千瓦时 超过a千瓦时的部分
单价(元/千瓦时) 0.5 0.6
小芳家二月份用电200千瓦时,交电费105元,则a= .
150
达标检测
5. 某城市按以下规定收取每月的燃气费:用气如果不超过60m3,按每立方米0.8元收费;如果超过60m3,超过部分按每立方米1.2元收费.已知某用户4月份燃气费平均每立方米0.88元,那么4月份这位用户应交燃气费多少元?
解:由4月份煤气费平均每立方米0.88元,
可得4月份用煤气一定超过60m3,
设4月份用了煤气x立方米,
由题意得:60×0.8+(x-60)×1.2=0.88×x,
解得x=75,则所交煤气费为75×0.88=66(元).
答:4月份这位用户应交煤气费66元.
达标检测
6. 我市某医药公司要把药品运往外地,现有两种运输方式可供选择:
方式一:使用快递公司的邮车运输,装卸收费400元,另外每公里运输路程再加收4元;
方式二:使用铁路运输公司的火车运输,装卸收费820元,另外每公里运输路程再加收2元.
你认为选用哪种运输方式较好,为什么?
达标检测
解:设运输路程为x公里,
则方式一的运输费用为(4x+400)元,
方式二的运输费用为(2x+820)元.
由4x+400=2x+820,解得x=210.综上所述,
可知当运输路程越大时,方式一的费用越多,
所以当运输路程小于210公里时,选择运输方式一较好;
当运输路程等于210公里时,选择两种运输方式费用一样多;
当运输路程大于210公里,选择运输方式二较好.
达标检测
分段计费问题
分清在未知数的不同取值范围内费用的不同计算方式
注意分类讨论,防止漏解
要对分类讨论求出的未知数的值进行检验,看它是否符合对应的取值范围
课堂总结
作业布置
教材练习1-3题
人教版 七年级上
3.4.2 解一元一次方程
-分段计费功能
学习目标
1.理解分段计费问题的原理,分清有关数量关系,能正确找出实际问题中蕴含的等量关系;
2.培养运用一元一次方程解决实际问题的能力;
3.体会分类思想和方程建模思想,增强应用意识和应用能力。
情境引入
哈密市出租车收费标准:行程不超过3千米,收起步价7元;超过部分每千米路程收费1.4元.(不足1千米按1千米计算)
老师下车时共付车费14元,问老师家到学校的距离?
情境引入
7
7
7
……
……
4
3
2.6
1.8
路程/km
费用/元
7+1.4×(4-3)=8.4
7+1.4( -3)
7+1.4×(5-3)=9.8
解:设老师家到学校有 千米。
列方程
7+1.4×( -3)=14
5
解得 =8
答:老师家到学校共8千米。
超出3km: + =总车费
起步车费
超过部分车费
>
3
分析下图中展示的通讯公司的通信套餐,小组讨论每一种套餐的优惠情况。
新知导入
下表给出的是两种移动电话的计费方式:
月使用费固定收
主叫不超限定时间不再收费
主叫超时,超时部分加收超时费
被叫免费
……
你能从表格中得到哪些信息呢?
新知讲解
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费/(元/分)
主叫限定时间/分
月使用
费/元
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
0
150
350
单位:min
方式一:
方式二:
计费与什么量有关系呢?
主叫时间
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费/(元/分)
主叫限定时间/分
月使用
费/元
新知讲解
你认为选择哪种计费方式更省钱呢?
设一个月内用移动电话主叫为t min(t是正整数).列表说明:当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
主叫时间t /分 方式一计费/元 方式二计费/元
t <150
t =150
150 < t <350
t =350
t >350
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
0
150
350
单位:min
t
方式一:
方式二:
58
58
58+0.25(t-150)
58+0.25(350-150)=108
58+0.25(t-150)
88
88
88
88
88+0.19(t-350)
新知讲解
设一个月内用移动电话主叫为t min(t是正整数).列表说明:当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
主叫时间t /分 方式一计费/元 方式二计费/元
t <150
t =150
150 < t <350
t =350
t >350
58
58
58+0.25(t-150)
58+0.25(350-150)=108
58+0.25(t-150)
88
88
88
88
88+0.19(t-350)
<
省钱
<
省钱
>
省钱
如何根据主叫时间选择省钱的计费方式?
新知讲解
解:令 58+0.25(t-150) =88
解得: t =270
∴当 t =270分时,两种计费方式的费用相等,
当150 < t < 270时,方式一的计费省钱;
和270 < t < 350时,方式二的计费省钱.
主叫时间t /分a 方式一计费/元 方式二计费/元
150 < t <350 58+0.25(t-150) 88
新知讲解
哪种方式省钱呢?
设一个月内用移动电话主叫为t min(t是正整数).列表说明:当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
主叫时间t /分 方式一计费/元 方式二计费/元
t <150
t =150
150 < t <350
t =350
t >350
58
58
58+0.25(t-150)
58+0.25(350-150)=108
58+0.25(t-150)
88
88
88
88
88+0.19(t-350)
<
省钱
<
省钱
>
省钱
新知讲解
如何根据主叫时间选择省钱的计费方式?
解:当t >350时,按方式一的计费为108元加上超出350min部分的超时费0.25(t-350)
按方式二的计费为88元加上超出350min部分的超时费0.19(t-350)
∴按方式二的计费省钱.
主叫时间t /分 方式一计费/元 方式二计费/元
t >350 58+0.25(t-150) 88+0.19(t-350)
新知讲解
哪种方式省钱呢?
综合以上的分析,可以发现:
时,选择方式一省钱;
时,选择方式二省钱.
t <270
t >270
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
单位:min
t
方式一:
方式二:
270
省钱
省钱
相等
新知讲解
分段计费问题解题思路:
1.在用含未知数的式子表示分段计费问题的费用时,要分清在未知数的不同取值范围内费用的不同计算方式,否则易混淆而出错.
2.若已知费用求未知数的值,要注意分类讨论,防止漏解,同时,要对分类讨论求出的未知数的值进行检验,看它是否符合对应的取值范围.
归纳
过关练习
某同学花了30元钱购买图书馆会员证,只限本人使用,凭证购入场券每张1元,不凭证购入场券每张4元,要想使得购会员证比不购会员证合算,该同学去图书馆阅览应超过( )
A.8次 B.9次 C.10次 D.11次
分析:设x次时两种方式花费相同,则
30+x=4x
解得 x=10
C
某校计划购买若干台电脑,现在从两家商场了解到同一型号的电脑每台报价均为4000元,甲商场经理说:“第一台按原报价收费,其余每台优惠25%.”乙商场经理说:“每台优惠20%.”
(1)若购买4台,哪家商场较优惠?买6台呢?
解:(1)购买4台时,
甲商场:4000+(1-0.25)×4000×3=13000(元)
乙商场: (1-0.20) ×4000×4=12800(元)
∴购买4台时,乙商场较优惠;
购买6台时,
甲商场:4000+(1-0.25)×4000×5=19000(元)
乙商场: (1-0.20) ×4000×6=19200(元)
购买6台时,甲商场较优惠.
过关练习
某校计划购买若干台电脑,现在从两家商场了解到同一型号的电脑每台报价均为4000元,甲商场经理说:“第一台按原报价收费,其余每台优惠25%.”乙商场经理说:“每台优惠20%.”
(2)买多少台,两家商场收费一样多?
解:(2)设买x台收费一样,列方程得
4000+0.75×4000(x-1) =0.8×4000x,
解得x=5,
∴买5台收费一样多.
过关练习
某校计划购买若干台电脑,现在从两家商场了解到同一型号的电脑每台报价均为4000元,甲商场经理说:“第一台按原报价收费,其余每台优惠25%.”乙商场经理说:“每台优惠20%.”
(3)你知道怎样选择更省钱吗?
解:(3)当购买数量少于5台时,选乙商场;
当购买数量超过5台时,选甲商场;
当购买数量为5台时,两商场收费一样多,可以从甲、乙两家商场中任选一家.
过关练习
要点 利用一元一次方程解计费问题
解答这类问题的一般步骤:运用一元一次方程解应用题的方法,求解使方案值 的情况;用特殊值试探去选择方案,取 一元一次方程解的值,比较两种方案的优劣后下结论.
相等
小于(或大于)
课堂小结
体验收获
今天我们学习了哪些知识?
1.电话计费问题的核心问题是什么?
2.探究解题的过程大致包含哪几个步骤?
3.我们在探究过程中用到了哪些方法,你有哪些收获?
1. 某电信公司的一种计费标准是:通话时间不超过3分钟,收话费0.2元,以后每分钟收话费0.1元,若小张的话费仅有2.4元,则他能持续通话的最长时间为( )
A. 23分钟 B. 24分钟 C. 25分钟 D. 26分钟
C
达标检测
2.有一旅客带30 kg行李从北京到广州,按民航规定,旅客最多可免费携带20 kg行李,超过部分每千克按飞机票价的1.5%购买行李票.已知该旅客购买的行李票为180元,则他的飞机票价为( )
A.800元 B.1000元 C.1200元 D.1400元
C
达标检测
3. 小明所在城市的“阶梯水价”收费办法是:每户用水不超过5吨,每吨水费x元;超过5吨,超过部分每吨加收2元,小明家今年5月份用水9吨,共交水费为44元,根据题意列出关于x的方程正确的是( )
A. 5x+4(x+2)=44 B. 5x+4(x-2)=44
C. 9(x+2)=44 D. 9(x+2)-4×2=44
A
达标检测
4. 某市居民用电价格改革方案已出台,为鼓励居民节约用电,对居民生活用电实行阶梯价,如下表:
“一户一表”用电量 不超过a千瓦时 超过a千瓦时的部分
单价(元/千瓦时) 0.5 0.6
小芳家二月份用电200千瓦时,交电费105元,则a= .
150
达标检测
5. 某城市按以下规定收取每月的燃气费:用气如果不超过60m3,按每立方米0.8元收费;如果超过60m3,超过部分按每立方米1.2元收费.已知某用户4月份燃气费平均每立方米0.88元,那么4月份这位用户应交燃气费多少元?
解:由4月份煤气费平均每立方米0.88元,
可得4月份用煤气一定超过60m3,
设4月份用了煤气x立方米,
由题意得:60×0.8+(x-60)×1.2=0.88×x,
解得x=75,则所交煤气费为75×0.88=66(元).
答:4月份这位用户应交煤气费66元.
达标检测
6. 我市某医药公司要把药品运往外地,现有两种运输方式可供选择:
方式一:使用快递公司的邮车运输,装卸收费400元,另外每公里运输路程再加收4元;
方式二:使用铁路运输公司的火车运输,装卸收费820元,另外每公里运输路程再加收2元.
你认为选用哪种运输方式较好,为什么?
达标检测
解:设运输路程为x公里,
则方式一的运输费用为(4x+400)元,
方式二的运输费用为(2x+820)元.
由4x+400=2x+820,解得x=210.综上所述,
可知当运输路程越大时,方式一的费用越多,
所以当运输路程小于210公里时,选择运输方式一较好;
当运输路程等于210公里时,选择两种运输方式费用一样多;
当运输路程大于210公里,选择运输方式二较好.
达标检测
分段计费问题
分清在未知数的不同取值范围内费用的不同计算方式
注意分类讨论,防止漏解
要对分类讨论求出的未知数的值进行检验,看它是否符合对应的取值范围
课堂总结
作业布置
教材练习1-3题
