2021-2022学年高二上学期生物人教版选择性必修2 1.2 种群的数量变化课件(51张ppt)
文档属性
| 名称 | 2021-2022学年高二上学期生物人教版选择性必修2 1.2 种群的数量变化课件(51张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 25.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 生物学 | ||
| 更新时间 | 2021-11-26 00:00:00 | ||
图片预览








文档简介
(共51张PPT)
第2节 种群数量的变化
问题探讨
我们的手上难免沾染细菌。细菌的繁殖速率很快,因而我们要常洗手。假设在营养和生存空间没有限制的情况下,某种细菌每20min就通过分裂繁殖一次。
1.第n代细菌数量的计算公式是什么?
设细菌的初始数量为N0;
第一次分裂产生的细菌为第一代,数量为N0×2; 第n代的数量为N0×2n。
2. 72h后,由一个细菌分裂产生的细菌数量是多少?
2216
3. 在一个培养瓶中,细菌的数量会一直按照这个公式描述的趋势增长吗?
不会,因为培养瓶中的营养物质和空间是有限的;该公式成立是在理想条件下的。
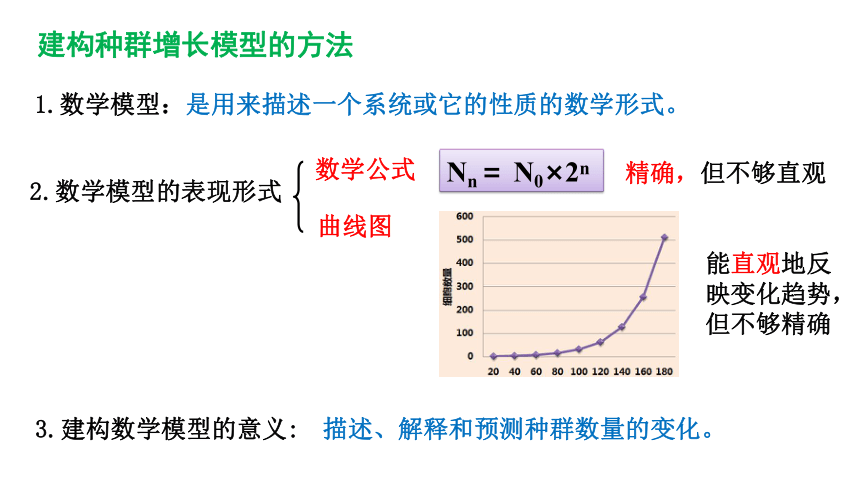
2.数学模型的表现形式
数学公式
曲线图
3.建构数学模型的意义:
描述、解释和预测种群数量的变化。
1.数学模型:是用来描述一个系统或它的性质的数学形式。
建构种群增长模型的方法
Nn= N0×2n
精确,但不够直观
能直观地反映变化趋势,但不够精确
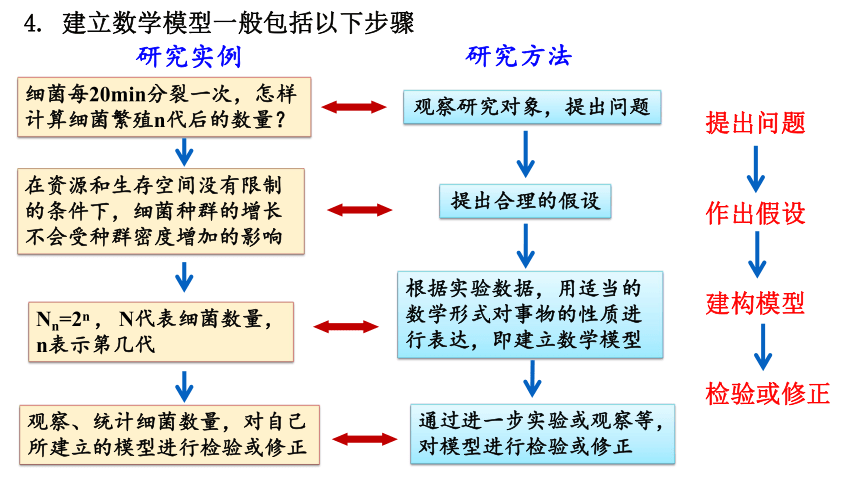
细菌每20min分裂一次,怎样计算细菌繁殖n代后的数量?
在资源和生存空间没有限制的条件下,细菌种群的增长不会受种群密度增加的影响
Nn=2n , N代表细菌数量,n表示第几代
观察、统计细菌数量,对自己所建立的模型进行检验或修正
研究实例
研究方法
观察研究对象,提出问题
提出合理的假设
根据实验数据,用适当的数学形式对事物的性质进行表达,即建立数学模型
通过进一步实验或观察等,对模型进行检验或修正
4. 建立数学模型一般包括以下步骤
提出问题
作出假设
建构模型
检验或修正
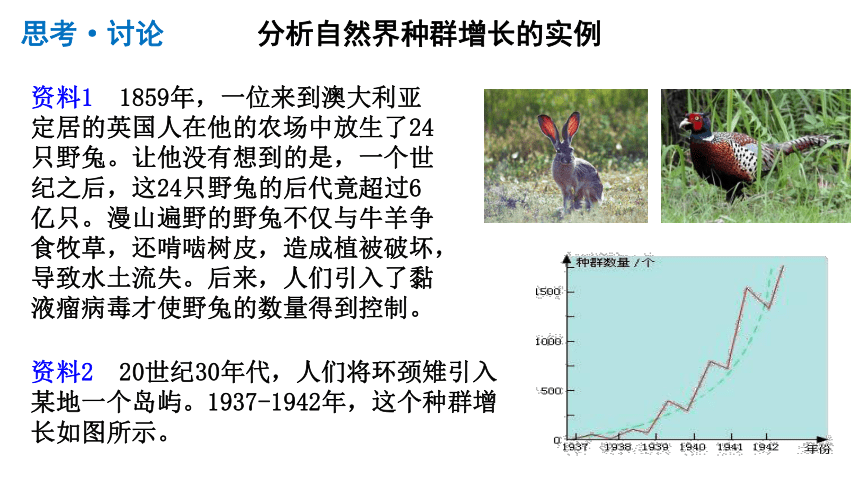
思考·讨论
分析自然界种群增长的实例
资料1 1859年,一位来到澳大利亚定居的英国人在他的农场中放生了24只野兔。让他没有想到的是,一个世纪之后,这24只野兔的后代竟超过6亿只。漫山遍野的野兔不仅与牛羊争食牧草,还啃啮树皮,造成植被破坏,导致水土流失。后来,人们引入了黏液瘤病毒才使野兔的数量得到控制。
资料2 20世纪30年代,人们将环颈雉引入某地一个岛屿。1937-1942年,这个种群增长如图所示。
1.这两个资料中种群增长有什么共同点
讨论
种群数量增长迅猛,且呈无限增长趋势。
2.种群出现这种增长的原因是什么?
食物充足,缺少天敌等。
3.这种种群增长的趋势能不能一直持续下去?为什么?
不能,因为资源和空间是有限的。
种群的“J”形增长
1.概念:自然界有类似细菌在理想条件下种群数量增长的形式,如果以时间为横坐标,种群数量为纵坐标画出曲线来表示,曲线则大致呈“J”型。这种类型的种群增长称为“J”型增长。
注意:该曲线的起点不是原点
2.“J”型增长的数学模型
(1)模型假设:
①条件:食物和空间条件充裕、气候适宜、
没有天敌和其他竞争物种(即无环境阻力)
思考:哪些情况下可能出现这种条件?
实验室条件下、迁移入新环境(如物种入侵)
思考:生物迁入新环境一定会出现J形增长吗?
不一定
(2)建立模型:t年后种群数量为Nt=N0×λt
参数含义:N0:该种群的起始数量
t:时间
Nt:表示t年后该种群的数量
λ:表示该种群数量是前一年种群数量的倍数
②数量变化:种群的数量每年以一定的倍数增长,第二年的数量是第一年的λ倍。
注意:J形增长的λ为定值;若λ不为定值,则说明种群数量变化非J形增长。
种群“J”型增长实例
凤眼莲(俗称水葫芦)原产于南美,1901年作为花卉引入中国。由于繁殖迅速,又几乎没有竞争对手和天敌,我国目前有184万吨。它对其生活的水面采取了野蛮的封锁策略,挡住阳光,导致水下植物得不到足够光照而死亡。
丹麦被生蚝入侵
众所周知,上个世纪30年代初的时候,日本侵华的原因,让很多日本人就因此来到我们国内生活。也为了制定发展计划,日本人带来了许多的入侵物种,其中最出名的就是学名克氏原螯虾的小龙虾,小龙虾原产于美洲,日本人从当地引进到了本土,之后在30年代左右的时候引入中国,在南京一代大量养殖。往后的岁月中,小龙虾迅速占领了亚热带的大多数池塘农田,因为拥有良好的排毒减毒机制,能够将这些污染最终会转移到壳体,通过不断蜕皮排到毒素,所以小龙虾能够适应各种各样的环境。也因为如此,中国人发现小龙虾能吃了之后,开始大量发展小龙虾料理,如今小龙虾已经成为国内最主要的经济淡水虾类,每年都被中国人吃到需要养殖来保证产量。
种群增长率与种群增长速率
①种群增长率:指种群在一定时间内增加的个体数占原来个体总数的比率,即增长率=(现有个体数-原有个体数)/原有个体数×100%
②种群增长速率:指单位时间内新增加的个体数(即种群数量增长曲线的斜率),增长速率=(现有个体数-原有个体数)/时间×100%
=(出生数-死亡数)/时间×100%
故增长率不能等同于增长速率
种群增长速率就是曲线上通过每一点的切线(即斜率)
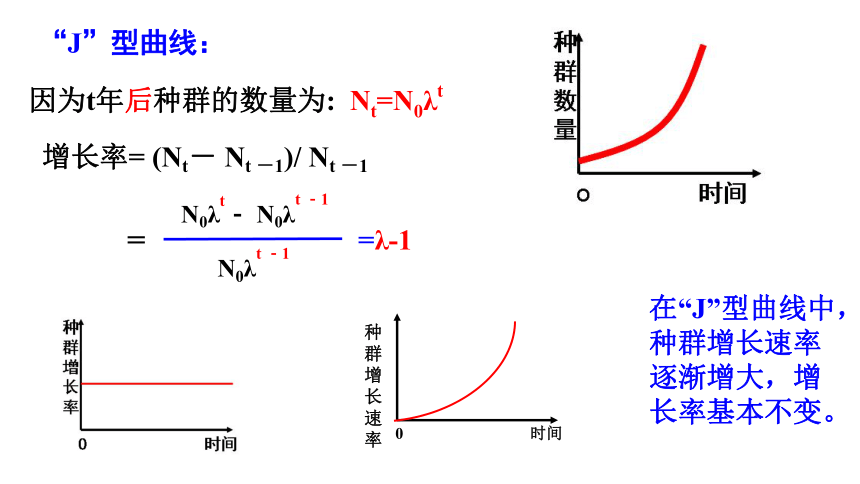
“J”型曲线:
因为t年后种群的数量为: Nt=N0λt
增长率= (Nt- Nt -1)/ Nt -1
N0λt- N0λt -1
N0λt -1
=
=λ-1
在“J”型曲线中,种群增长速率逐渐增大,增长率基本不变。
0 时间
种群增长速率
【思考1】
①当λ=1时,种群数量如何变化?
②当λ>1时,种群数量如何变化?
③当0<λ<1时,种群数量如何变化?
④当λ=0时,种群数量如何变化?
【思考2】当λ>1时,种群一定呈“J”形增长吗?
增长率=0,种群数量不变(相对稳定)
增长率>0, 种群数量增长
增长率<0,种群数量下降
不一定;只有λ>1且为定值时,种群增长才为“J”形增长。
λ
现有个体数
原有个体数
=
雌体没有繁殖,种群在下一代中灭亡
现学现用:据图说出种群数量如何变化
1-4年,种群数量_______________
4-5年,种群数量_______________
5-9年,种群数量_______________
9-10年,种群数量______________
10-11年,种群数量_____________
11-13年,种群数量___________ __
前9年,种群数量第_______年最高
9-13年,种群数量第______年最低
呈“J”形增长
增长
相对稳定
下降
下降
11-12下降,12-13增长
5
12
种群增长的“S”型曲线
生态学家高斯对大草履虫种群研究的实验:
在0.5mL培养液中放入5个大草履虫,然后每隔24 小时统计一次数据,经过反复实验,结果如下:
时间(D) 种群大小
1 20.4
2 137.2
3 319.0
4 369.0
5 375.3
6 375.4
像这样,种群经过一定时间的增长后,数量趋于稳定,增长曲线呈“S”形,这种类型的种群增长称为“S”形增长。
①模型假设:资源和空间有限,天敌的制约等(即存在环境阻力)
②建立模型: 一定的环境条件所能维持的种群最大数量称为环境容纳量,又称K值。
③曲线图分析:
ab段(适应期):种群基数小,需要适应新
环境,增长较缓慢。
bc段(加速期):资源和空间丰富,出生率
升高,种群数量增长迅速。
c点(转折期):出生率大于死亡率, 此时种群增长速率最大。
cd段(减速期):资源和空间有限,种群密度增大,种内竞争加剧,出生率降低,死亡率升高,种群增长减缓。
de段(饱和期):出生率约等于死亡率,种群增长速率几乎为0,种群数量达到K值,且维持相对稳定。种群数量达到最大,且种内斗争最剧。
思考:1、自然条件下,为什么种群增长到K值左右便会趋于稳定?
自然条件下,资源和空间总是有限的。
当种群密度增大时,种内竞争就会加剧,这就会使种群的出生率降低,死亡率升高。
当死亡率升高至与出生率相等时,种群的增长就会停止,有时会稳定在一定的水平(K值)。
种内竞争对种群数量起调节作用。
2.种群数量到达K值后就不再变化了吗?
3.K值是不是种群数量的最大值?
4.同一种群的K值是固定不变的吗?
在K值上下波动,动态平衡
不是;K值是种群在一定环境条件下所能维持的种群最大数量
不是;
食物减少和活动范围缩小等不利条件下,K值会变小;
食物充足和生存空间扩大等有利条件下,K值会增大。
“S”型曲线
S形曲线的增长速率先变大,在种群数量为K/2时达到最大,后逐渐减小,直至为零(K值)
*种群数量曲线不能从原点出发,增长速率曲线可以从原点出发
K值和1/2K值的应用
(1)野生生物的保护
应对措施:
建立自然保护区,提供更宽广的生存空间,改善它们的栖息环境,减小环境阻力,从而提高环境容纳量(K值),是保护它们的根本措施。
野生大熊猫数量锐减的原因:
栖息地遭到破坏,食物减少和活动范围缩小,K 值变小。
①从环境容纳量考虑:增大环境阻力,降低环境容纳量。
(2)有害生物的防治
例如:将粮食和其他食物储藏在安全处,断绝或减少它们的食物来源;室内采取硬化地面等措施,减少它们挖造巢穴的场所;养殖或释放它们的天敌;搞好环境卫生;等等。
②从1/2K值考虑:在种群增长刚开始(达到1/2K之前)的时候就进行防治;(绝对不能让种群数量增长到1/2K值)
(3)资源的合理利用
捕鱼时,在刚超过1/2K时开始捕捞;要使被捕种群的剩余量维持在1/2K附近。
目的:以持续获得最大的捕捞量
种群数量>K/2时是最佳捕捞时期!
草原最大载畜量不超过K值→合理确定载畜量
最大捕捞量≠最大日捕获量
①要持续获得最大捕捞量:K/2之后捕捞
②要获得日捕获量:应在种群密度最大时捕捞(即K值时)
1.“J”型曲线用达尔文的观点分析表明生物具有过度繁殖的特性。
2.图中阴影部分表示:环境阻力;用达尔文的观点分析指:通过生存斗争被淘汰的个体数量,也即代表自然选择的作用。
用达尔文的观点分析“J”、“S”型曲线
时间
种群数量
J型曲线
S型曲线
K值
“J”型曲线无 K值, 无种内斗争, 无天敌。
种群在没有环境阻力的条件下呈现“J”型增长,实际上是“S”型增长的最初阶段, “J”型增长是一定时间内的增长方式,最终是以”S”型增长结束,这是生态因素和物种本身相互影响的结果。
4. 在环境不遭受破坏的情况下, 种群数量会在 上下波动。当种群数量偏离K值的时候,会通过 调节使种群数量回到K值。
3. 同一种生物的K值不是固定不变的:
K值会随着环境的改变而发生变化, 当
环境遭受破坏时,K值变化是 ;
当环境条件状况改善时,K值会 。
负反馈
下降
上升
K值附近
5. K值并不是种群数量的最大值:
K值是环境容纳量,即在保证环境不被破坏的前提下所能容纳的最大值;种群所达到的最大值会超过K值,但这个值存在的时间很短,因为环境已遭到破坏。
K值的四种表示方法
(1)① 对应的种群增长速率为0,
数量最大,为K值。
② 对应的种群增长速率最大,为K/2值。
(2)B点对应的种群出生率与死亡率相等,种群数量达到最大,为 。
A点
A'点
K值
(3)① 对应的种群数量为K值。
② 对应的种群出生率与死亡率差值最大,为K/2值。
(4)① 对应的种群个体数最多,即K值。
② 对应的种群个体数为K/2值。
C点
C'点
D点
D'点
种群增长的两种曲线的比较
J型曲线 S型曲线
条件
特点
有无K值
曲线 环境资源无限
环境资源有限
连续增长
增长到K值后稳定
无
有K值
环境阻力
食物不足
空间有限
种内斗争
天敌捕食
气候不适
寄生虫
传染病等
K值:环境容纳量
种群数量的波动
②但对于大多数生物的种群来说,种群数量总是在波动中。处在波动状态的种群,在特定条件下可能出现种群爆发。如蝗灾、赤潮等。
东亚飞蝗种群数量的波动
①在自然界,有的种群能够在一段时间内维持数量的相对稳定。
③当种群长期处于不利条件下,种群数量会出现持续性或急剧的下降;如遭遇人类乱捕滥杀和栖息地破坏。
种群的延续需要有一定的个体数量为基础;当一个种群的数量过少,种群可能会由于近亲繁殖等原因而衰退、消亡。
*对于那些已经低于种群延续所需要的最小种群数量的物种,需要采取有效的措施进行保护。
环境因素
种群的出生率、死亡率、迁出和迁入率
种群数量的变化
食物、气候、天敌、传染病等
增或减
增长、波动、稳定、下降等
影响种群数量变化的因素
直接因素:出生率、死亡率、迁入、迁出
间接因素:年龄组成和性别比例
重要因素:人类的活动
自然因素:食物、气候、天敌、传染病等
(1)有利于野生生物资源的合理利用及保护。
(2)为人工养殖及种植业中合理控制种群数量、适时捕捞、采伐等提供理论指导。
(3)通过研究种群数量变动规律,为害虫的预测及防治提供科学依据。
(4)有利于对濒危动物种群的拯救和恢复。
研究种群数量变化的意义
酿酒和做面包都需要酵母菌,这些酵母菌可以用液体培养基(培养液)来培养。培养液中酵母菌种群的增长情况,与发酵食品的制作有密切关系。
培养液中酵母菌种群数量的变化
探究·实践
1.单细胞真核生物
2.兼性厌氧菌
3.出芽生殖
1.实验目的:初步学会酵母菌等微生物的计数及种群数量变化曲线的绘制。
2.实验原理:用液体培养基(培养液)培养酵母菌,种群的增长受培养液的成分、空间、pH、温度等因素的影响。
3.提出问题:培养液中酵母菌种群的数量是怎样随时间变化的?
4.材料用具:酵母菌、无菌马铃薯培养液或肉汤培养液、试管、血细胞计数板、滴管、显微镜等。
5.讨论思路:
自变量:
因变量:
无关变量:
时间
酵母菌数量
培养液的体积等
计数室
1mm
大方格的长和宽各为1mm,深度为0.1mm,即1mm×1mm×0.1mm,其容积为0.1mm3
计数室
血细胞计数板:专门用于计数单细胞微生物的一种仪器
1个计数室的面积为1mm2 ,1个计数
室内有400个小方格。每个小方格的面积1/400mm2
② 1/400mm2的含义
① 0.10mm的含义
计数室的深度为0.1mm
计数室通常有两种规格:
25×16型:即大方格内分为25中格,每一中格又分为16小格
16×25型:即大方格内分为16中格,每一中格又分为25小格
不管计数室是哪一种构造,其每一大方格都是由16×25=25×16=400个小方格组成
取样方法:如图B所示,25中格×16小格的计数板,需要对四个顶角及中央5个中格中的酵母菌进行计数;如图C所示,16中格×25小格的计数板,则只需对四个顶角中格中的酵母菌进行计数。随后估算出每个小方格中的酵母菌数。
(1)怎样对酵母菌进行计数?
采用抽样检测的方法:
先将盖玻片放在血细胞计数板的计数室上,用吸管吸取培养液,滴于盖玻片边缘,让培养液自行渗入。多余的培养液用滤纸吸去。稍待片刻,待酵母菌全部沉降到计数室底部,将计数板放在载物台的中央,计数一个小方格内的酵母菌数量,在以此为根据,估算酵母菌数量。
如果先加培养液再盖盖玻片,那么盖玻片可能由于已加入液滴的表面张力而不能严密地盖到计数板表面,使计数室内部液体增多,导致计数结果偏高。
说明:大方格体积=0.1立方毫米,每个大方格共分为25个中方格,共有25×16=400个小方格
1mL培养液中细胞个数=每小方格中细胞的个数×400 ×104×稀释倍数
1 mL培养液中细胞个数=中方格中酵母菌数量的平均值×25×104 ×稀释倍数
1.从试管中吸出培养液进行计数之前,建议你将试管轻轻振荡几次。这是为什么?
目的是使培养液中的酵母菌均匀分布,以保证估算的准确性,减少误差。
2.如果一个小方格内酵母菌过多,难以计数,应采取怎样的措施?
稀释一定倍数后,再用血球计数板计数
思考
用无菌水稀释至每小格细胞数目为5~10 个
稀释100倍
只计数相邻两边及其夹角的酵母菌数。
(计上不计下,计左不计右)
3.对于压在小方格界线上的酵母菌,应当怎样计数?
4.为什么要待酵母菌全部沉降到计数室底部再计数?
酵母菌全部沉降到计数室底部,减少实验误差。
5.本探究需要设置对照吗?如果需要请讨论对照组应怎样设计和操作;如果不需要,请说明理由。
酵母菌在不同时间内的数量可以形成自身前后对照,不需另设对照实验。
6.需要做重复实验吗?
需要重复实验,以提高实验数据的准确性;对每个样品可计数三次,再取平均值
7.怎么分辨死亡细胞和有活性的细胞?
死亡细胞多集结成团;
可以借助台盼蓝染色(死亡细胞呈蓝色)
第0天 第1天 第2天 第3天 第4天 第5天 第6天
第1组
第2组
第3组
------
第n组
平均值
8.怎样记录结果?记录表怎样设计?
实施计划
首先通过显微镜观察,估算出10mL培养液中酵母菌的初始数量(N0),在此之后连续观察7天,分布记录下这7天的数值
第1天
第4天
第6天
第7天
死亡
分析结果,得出结论
酵母菌增长曲线分析
酵母菌增长的总趋势是先增加再降低。
原因是在开始时培养液的营养充足、空间充裕、条件适宜,因此酵母菌大量繁殖,种群数量剧增。
随着酵母菌数量的不断增多,营养消耗、pH变化、有害代谢产物积累等,使生存条件恶化,酵母菌死亡率高于出生率,种群数量下降。
注意事项
(1)取样时间需一致,且应做到随机取样(每天同一时间取样,或者每隔相同一段时间取样)
(2)抽取样液之前,需要振荡,使酵母菌均匀分布,如果未振荡试管就吸出培养液,可能出现两种情况:一是从试管下部吸取的培养液浓度偏大;二是从试管上部吸出的培养液浓度偏小。因为酵母菌会沉降在瓶底。
(3)若保持培养条件,酵母菌种群数量不会一直保持稳定,将会下降,因为营养物质减少、代谢废物增多、空间有限、pH降低等。
(4)血细胞计数板使用完毕后,用水冲洗干净或浸泡在酒精溶液中,切勿用硬物洗刷或抹擦,以免损坏网格刻度。
[检测] “S”型曲线与其增长速率的关系
K/2
t0 t1 t2 时间
种群数量
K
a
b
c
d
e
⑴图乙的fg段相当于图甲的 段
⑵图乙的g点相当于图甲的 点
⑶图乙的gh段相当于图甲的 段
⑷图乙的h点相当于图甲的 段
甲
乙
增长速率变化:
0~K/2时逐渐增大
K/2~K时逐渐减小
在 K/2时达到最大
在K时增长速率为0
ac
c
cd
de
t0 t1 t2 时间
0 K/2 K 数量
增长速率
f
g
h
种群数量的变化
种群增长模型
建构种群增长模型的方法
种群的“S”形增长
种群的“J”形增长
自然种群的数量变动
条件:食物和空间充裕、气候适宜、无天敌和其他竞争物种
特点:种群数量每年以一定倍数增长
一段时间内相对稳定(接近K值)
条件:食物和空间有限
特点:种群增长速率先增大后减小,最后为0
K值:一定环境条件下所能维持的种群最大数量
探究培养液中酵母菌种群数量变化(验证种群数量增长模型)
持续性的或急剧的下降,甚至衰退和消亡
规则或不规则波动。(K值是种群数量波动的平均值,波动中的生物,在某些特定条件下可能出现种群爆发)
小结
第2节 种群数量的变化
问题探讨
我们的手上难免沾染细菌。细菌的繁殖速率很快,因而我们要常洗手。假设在营养和生存空间没有限制的情况下,某种细菌每20min就通过分裂繁殖一次。
1.第n代细菌数量的计算公式是什么?
设细菌的初始数量为N0;
第一次分裂产生的细菌为第一代,数量为N0×2; 第n代的数量为N0×2n。
2. 72h后,由一个细菌分裂产生的细菌数量是多少?
2216
3. 在一个培养瓶中,细菌的数量会一直按照这个公式描述的趋势增长吗?
不会,因为培养瓶中的营养物质和空间是有限的;该公式成立是在理想条件下的。
2.数学模型的表现形式
数学公式
曲线图
3.建构数学模型的意义:
描述、解释和预测种群数量的变化。
1.数学模型:是用来描述一个系统或它的性质的数学形式。
建构种群增长模型的方法
Nn= N0×2n
精确,但不够直观
能直观地反映变化趋势,但不够精确
细菌每20min分裂一次,怎样计算细菌繁殖n代后的数量?
在资源和生存空间没有限制的条件下,细菌种群的增长不会受种群密度增加的影响
Nn=2n , N代表细菌数量,n表示第几代
观察、统计细菌数量,对自己所建立的模型进行检验或修正
研究实例
研究方法
观察研究对象,提出问题
提出合理的假设
根据实验数据,用适当的数学形式对事物的性质进行表达,即建立数学模型
通过进一步实验或观察等,对模型进行检验或修正
4. 建立数学模型一般包括以下步骤
提出问题
作出假设
建构模型
检验或修正
思考·讨论
分析自然界种群增长的实例
资料1 1859年,一位来到澳大利亚定居的英国人在他的农场中放生了24只野兔。让他没有想到的是,一个世纪之后,这24只野兔的后代竟超过6亿只。漫山遍野的野兔不仅与牛羊争食牧草,还啃啮树皮,造成植被破坏,导致水土流失。后来,人们引入了黏液瘤病毒才使野兔的数量得到控制。
资料2 20世纪30年代,人们将环颈雉引入某地一个岛屿。1937-1942年,这个种群增长如图所示。
1.这两个资料中种群增长有什么共同点
讨论
种群数量增长迅猛,且呈无限增长趋势。
2.种群出现这种增长的原因是什么?
食物充足,缺少天敌等。
3.这种种群增长的趋势能不能一直持续下去?为什么?
不能,因为资源和空间是有限的。
种群的“J”形增长
1.概念:自然界有类似细菌在理想条件下种群数量增长的形式,如果以时间为横坐标,种群数量为纵坐标画出曲线来表示,曲线则大致呈“J”型。这种类型的种群增长称为“J”型增长。
注意:该曲线的起点不是原点
2.“J”型增长的数学模型
(1)模型假设:
①条件:食物和空间条件充裕、气候适宜、
没有天敌和其他竞争物种(即无环境阻力)
思考:哪些情况下可能出现这种条件?
实验室条件下、迁移入新环境(如物种入侵)
思考:生物迁入新环境一定会出现J形增长吗?
不一定
(2)建立模型:t年后种群数量为Nt=N0×λt
参数含义:N0:该种群的起始数量
t:时间
Nt:表示t年后该种群的数量
λ:表示该种群数量是前一年种群数量的倍数
②数量变化:种群的数量每年以一定的倍数增长,第二年的数量是第一年的λ倍。
注意:J形增长的λ为定值;若λ不为定值,则说明种群数量变化非J形增长。
种群“J”型增长实例
凤眼莲(俗称水葫芦)原产于南美,1901年作为花卉引入中国。由于繁殖迅速,又几乎没有竞争对手和天敌,我国目前有184万吨。它对其生活的水面采取了野蛮的封锁策略,挡住阳光,导致水下植物得不到足够光照而死亡。
丹麦被生蚝入侵
众所周知,上个世纪30年代初的时候,日本侵华的原因,让很多日本人就因此来到我们国内生活。也为了制定发展计划,日本人带来了许多的入侵物种,其中最出名的就是学名克氏原螯虾的小龙虾,小龙虾原产于美洲,日本人从当地引进到了本土,之后在30年代左右的时候引入中国,在南京一代大量养殖。往后的岁月中,小龙虾迅速占领了亚热带的大多数池塘农田,因为拥有良好的排毒减毒机制,能够将这些污染最终会转移到壳体,通过不断蜕皮排到毒素,所以小龙虾能够适应各种各样的环境。也因为如此,中国人发现小龙虾能吃了之后,开始大量发展小龙虾料理,如今小龙虾已经成为国内最主要的经济淡水虾类,每年都被中国人吃到需要养殖来保证产量。
种群增长率与种群增长速率
①种群增长率:指种群在一定时间内增加的个体数占原来个体总数的比率,即增长率=(现有个体数-原有个体数)/原有个体数×100%
②种群增长速率:指单位时间内新增加的个体数(即种群数量增长曲线的斜率),增长速率=(现有个体数-原有个体数)/时间×100%
=(出生数-死亡数)/时间×100%
故增长率不能等同于增长速率
种群增长速率就是曲线上通过每一点的切线(即斜率)
“J”型曲线:
因为t年后种群的数量为: Nt=N0λt
增长率= (Nt- Nt -1)/ Nt -1
N0λt- N0λt -1
N0λt -1
=
=λ-1
在“J”型曲线中,种群增长速率逐渐增大,增长率基本不变。
0 时间
种群增长速率
【思考1】
①当λ=1时,种群数量如何变化?
②当λ>1时,种群数量如何变化?
③当0<λ<1时,种群数量如何变化?
④当λ=0时,种群数量如何变化?
【思考2】当λ>1时,种群一定呈“J”形增长吗?
增长率=0,种群数量不变(相对稳定)
增长率>0, 种群数量增长
增长率<0,种群数量下降
不一定;只有λ>1且为定值时,种群增长才为“J”形增长。
λ
现有个体数
原有个体数
=
雌体没有繁殖,种群在下一代中灭亡
现学现用:据图说出种群数量如何变化
1-4年,种群数量_______________
4-5年,种群数量_______________
5-9年,种群数量_______________
9-10年,种群数量______________
10-11年,种群数量_____________
11-13年,种群数量___________ __
前9年,种群数量第_______年最高
9-13年,种群数量第______年最低
呈“J”形增长
增长
相对稳定
下降
下降
11-12下降,12-13增长
5
12
种群增长的“S”型曲线
生态学家高斯对大草履虫种群研究的实验:
在0.5mL培养液中放入5个大草履虫,然后每隔24 小时统计一次数据,经过反复实验,结果如下:
时间(D) 种群大小
1 20.4
2 137.2
3 319.0
4 369.0
5 375.3
6 375.4
像这样,种群经过一定时间的增长后,数量趋于稳定,增长曲线呈“S”形,这种类型的种群增长称为“S”形增长。
①模型假设:资源和空间有限,天敌的制约等(即存在环境阻力)
②建立模型: 一定的环境条件所能维持的种群最大数量称为环境容纳量,又称K值。
③曲线图分析:
ab段(适应期):种群基数小,需要适应新
环境,增长较缓慢。
bc段(加速期):资源和空间丰富,出生率
升高,种群数量增长迅速。
c点(转折期):出生率大于死亡率, 此时种群增长速率最大。
cd段(减速期):资源和空间有限,种群密度增大,种内竞争加剧,出生率降低,死亡率升高,种群增长减缓。
de段(饱和期):出生率约等于死亡率,种群增长速率几乎为0,种群数量达到K值,且维持相对稳定。种群数量达到最大,且种内斗争最剧。
思考:1、自然条件下,为什么种群增长到K值左右便会趋于稳定?
自然条件下,资源和空间总是有限的。
当种群密度增大时,种内竞争就会加剧,这就会使种群的出生率降低,死亡率升高。
当死亡率升高至与出生率相等时,种群的增长就会停止,有时会稳定在一定的水平(K值)。
种内竞争对种群数量起调节作用。
2.种群数量到达K值后就不再变化了吗?
3.K值是不是种群数量的最大值?
4.同一种群的K值是固定不变的吗?
在K值上下波动,动态平衡
不是;K值是种群在一定环境条件下所能维持的种群最大数量
不是;
食物减少和活动范围缩小等不利条件下,K值会变小;
食物充足和生存空间扩大等有利条件下,K值会增大。
“S”型曲线
S形曲线的增长速率先变大,在种群数量为K/2时达到最大,后逐渐减小,直至为零(K值)
*种群数量曲线不能从原点出发,增长速率曲线可以从原点出发
K值和1/2K值的应用
(1)野生生物的保护
应对措施:
建立自然保护区,提供更宽广的生存空间,改善它们的栖息环境,减小环境阻力,从而提高环境容纳量(K值),是保护它们的根本措施。
野生大熊猫数量锐减的原因:
栖息地遭到破坏,食物减少和活动范围缩小,K 值变小。
①从环境容纳量考虑:增大环境阻力,降低环境容纳量。
(2)有害生物的防治
例如:将粮食和其他食物储藏在安全处,断绝或减少它们的食物来源;室内采取硬化地面等措施,减少它们挖造巢穴的场所;养殖或释放它们的天敌;搞好环境卫生;等等。
②从1/2K值考虑:在种群增长刚开始(达到1/2K之前)的时候就进行防治;(绝对不能让种群数量增长到1/2K值)
(3)资源的合理利用
捕鱼时,在刚超过1/2K时开始捕捞;要使被捕种群的剩余量维持在1/2K附近。
目的:以持续获得最大的捕捞量
种群数量>K/2时是最佳捕捞时期!
草原最大载畜量不超过K值→合理确定载畜量
最大捕捞量≠最大日捕获量
①要持续获得最大捕捞量:K/2之后捕捞
②要获得日捕获量:应在种群密度最大时捕捞(即K值时)
1.“J”型曲线用达尔文的观点分析表明生物具有过度繁殖的特性。
2.图中阴影部分表示:环境阻力;用达尔文的观点分析指:通过生存斗争被淘汰的个体数量,也即代表自然选择的作用。
用达尔文的观点分析“J”、“S”型曲线
时间
种群数量
J型曲线
S型曲线
K值
“J”型曲线无 K值, 无种内斗争, 无天敌。
种群在没有环境阻力的条件下呈现“J”型增长,实际上是“S”型增长的最初阶段, “J”型增长是一定时间内的增长方式,最终是以”S”型增长结束,这是生态因素和物种本身相互影响的结果。
4. 在环境不遭受破坏的情况下, 种群数量会在 上下波动。当种群数量偏离K值的时候,会通过 调节使种群数量回到K值。
3. 同一种生物的K值不是固定不变的:
K值会随着环境的改变而发生变化, 当
环境遭受破坏时,K值变化是 ;
当环境条件状况改善时,K值会 。
负反馈
下降
上升
K值附近
5. K值并不是种群数量的最大值:
K值是环境容纳量,即在保证环境不被破坏的前提下所能容纳的最大值;种群所达到的最大值会超过K值,但这个值存在的时间很短,因为环境已遭到破坏。
K值的四种表示方法
(1)① 对应的种群增长速率为0,
数量最大,为K值。
② 对应的种群增长速率最大,为K/2值。
(2)B点对应的种群出生率与死亡率相等,种群数量达到最大,为 。
A点
A'点
K值
(3)① 对应的种群数量为K值。
② 对应的种群出生率与死亡率差值最大,为K/2值。
(4)① 对应的种群个体数最多,即K值。
② 对应的种群个体数为K/2值。
C点
C'点
D点
D'点
种群增长的两种曲线的比较
J型曲线 S型曲线
条件
特点
有无K值
曲线 环境资源无限
环境资源有限
连续增长
增长到K值后稳定
无
有K值
环境阻力
食物不足
空间有限
种内斗争
天敌捕食
气候不适
寄生虫
传染病等
K值:环境容纳量
种群数量的波动
②但对于大多数生物的种群来说,种群数量总是在波动中。处在波动状态的种群,在特定条件下可能出现种群爆发。如蝗灾、赤潮等。
东亚飞蝗种群数量的波动
①在自然界,有的种群能够在一段时间内维持数量的相对稳定。
③当种群长期处于不利条件下,种群数量会出现持续性或急剧的下降;如遭遇人类乱捕滥杀和栖息地破坏。
种群的延续需要有一定的个体数量为基础;当一个种群的数量过少,种群可能会由于近亲繁殖等原因而衰退、消亡。
*对于那些已经低于种群延续所需要的最小种群数量的物种,需要采取有效的措施进行保护。
环境因素
种群的出生率、死亡率、迁出和迁入率
种群数量的变化
食物、气候、天敌、传染病等
增或减
增长、波动、稳定、下降等
影响种群数量变化的因素
直接因素:出生率、死亡率、迁入、迁出
间接因素:年龄组成和性别比例
重要因素:人类的活动
自然因素:食物、气候、天敌、传染病等
(1)有利于野生生物资源的合理利用及保护。
(2)为人工养殖及种植业中合理控制种群数量、适时捕捞、采伐等提供理论指导。
(3)通过研究种群数量变动规律,为害虫的预测及防治提供科学依据。
(4)有利于对濒危动物种群的拯救和恢复。
研究种群数量变化的意义
酿酒和做面包都需要酵母菌,这些酵母菌可以用液体培养基(培养液)来培养。培养液中酵母菌种群的增长情况,与发酵食品的制作有密切关系。
培养液中酵母菌种群数量的变化
探究·实践
1.单细胞真核生物
2.兼性厌氧菌
3.出芽生殖
1.实验目的:初步学会酵母菌等微生物的计数及种群数量变化曲线的绘制。
2.实验原理:用液体培养基(培养液)培养酵母菌,种群的增长受培养液的成分、空间、pH、温度等因素的影响。
3.提出问题:培养液中酵母菌种群的数量是怎样随时间变化的?
4.材料用具:酵母菌、无菌马铃薯培养液或肉汤培养液、试管、血细胞计数板、滴管、显微镜等。
5.讨论思路:
自变量:
因变量:
无关变量:
时间
酵母菌数量
培养液的体积等
计数室
1mm
大方格的长和宽各为1mm,深度为0.1mm,即1mm×1mm×0.1mm,其容积为0.1mm3
计数室
血细胞计数板:专门用于计数单细胞微生物的一种仪器
1个计数室的面积为1mm2 ,1个计数
室内有400个小方格。每个小方格的面积1/400mm2
② 1/400mm2的含义
① 0.10mm的含义
计数室的深度为0.1mm
计数室通常有两种规格:
25×16型:即大方格内分为25中格,每一中格又分为16小格
16×25型:即大方格内分为16中格,每一中格又分为25小格
不管计数室是哪一种构造,其每一大方格都是由16×25=25×16=400个小方格组成
取样方法:如图B所示,25中格×16小格的计数板,需要对四个顶角及中央5个中格中的酵母菌进行计数;如图C所示,16中格×25小格的计数板,则只需对四个顶角中格中的酵母菌进行计数。随后估算出每个小方格中的酵母菌数。
(1)怎样对酵母菌进行计数?
采用抽样检测的方法:
先将盖玻片放在血细胞计数板的计数室上,用吸管吸取培养液,滴于盖玻片边缘,让培养液自行渗入。多余的培养液用滤纸吸去。稍待片刻,待酵母菌全部沉降到计数室底部,将计数板放在载物台的中央,计数一个小方格内的酵母菌数量,在以此为根据,估算酵母菌数量。
如果先加培养液再盖盖玻片,那么盖玻片可能由于已加入液滴的表面张力而不能严密地盖到计数板表面,使计数室内部液体增多,导致计数结果偏高。
说明:大方格体积=0.1立方毫米,每个大方格共分为25个中方格,共有25×16=400个小方格
1mL培养液中细胞个数=每小方格中细胞的个数×400 ×104×稀释倍数
1 mL培养液中细胞个数=中方格中酵母菌数量的平均值×25×104 ×稀释倍数
1.从试管中吸出培养液进行计数之前,建议你将试管轻轻振荡几次。这是为什么?
目的是使培养液中的酵母菌均匀分布,以保证估算的准确性,减少误差。
2.如果一个小方格内酵母菌过多,难以计数,应采取怎样的措施?
稀释一定倍数后,再用血球计数板计数
思考
用无菌水稀释至每小格细胞数目为5~10 个
稀释100倍
只计数相邻两边及其夹角的酵母菌数。
(计上不计下,计左不计右)
3.对于压在小方格界线上的酵母菌,应当怎样计数?
4.为什么要待酵母菌全部沉降到计数室底部再计数?
酵母菌全部沉降到计数室底部,减少实验误差。
5.本探究需要设置对照吗?如果需要请讨论对照组应怎样设计和操作;如果不需要,请说明理由。
酵母菌在不同时间内的数量可以形成自身前后对照,不需另设对照实验。
6.需要做重复实验吗?
需要重复实验,以提高实验数据的准确性;对每个样品可计数三次,再取平均值
7.怎么分辨死亡细胞和有活性的细胞?
死亡细胞多集结成团;
可以借助台盼蓝染色(死亡细胞呈蓝色)
第0天 第1天 第2天 第3天 第4天 第5天 第6天
第1组
第2组
第3组
------
第n组
平均值
8.怎样记录结果?记录表怎样设计?
实施计划
首先通过显微镜观察,估算出10mL培养液中酵母菌的初始数量(N0),在此之后连续观察7天,分布记录下这7天的数值
第1天
第4天
第6天
第7天
死亡
分析结果,得出结论
酵母菌增长曲线分析
酵母菌增长的总趋势是先增加再降低。
原因是在开始时培养液的营养充足、空间充裕、条件适宜,因此酵母菌大量繁殖,种群数量剧增。
随着酵母菌数量的不断增多,营养消耗、pH变化、有害代谢产物积累等,使生存条件恶化,酵母菌死亡率高于出生率,种群数量下降。
注意事项
(1)取样时间需一致,且应做到随机取样(每天同一时间取样,或者每隔相同一段时间取样)
(2)抽取样液之前,需要振荡,使酵母菌均匀分布,如果未振荡试管就吸出培养液,可能出现两种情况:一是从试管下部吸取的培养液浓度偏大;二是从试管上部吸出的培养液浓度偏小。因为酵母菌会沉降在瓶底。
(3)若保持培养条件,酵母菌种群数量不会一直保持稳定,将会下降,因为营养物质减少、代谢废物增多、空间有限、pH降低等。
(4)血细胞计数板使用完毕后,用水冲洗干净或浸泡在酒精溶液中,切勿用硬物洗刷或抹擦,以免损坏网格刻度。
[检测] “S”型曲线与其增长速率的关系
K/2
t0 t1 t2 时间
种群数量
K
a
b
c
d
e
⑴图乙的fg段相当于图甲的 段
⑵图乙的g点相当于图甲的 点
⑶图乙的gh段相当于图甲的 段
⑷图乙的h点相当于图甲的 段
甲
乙
增长速率变化:
0~K/2时逐渐增大
K/2~K时逐渐减小
在 K/2时达到最大
在K时增长速率为0
ac
c
cd
de
t0 t1 t2 时间
0 K/2 K 数量
增长速率
f
g
h
种群数量的变化
种群增长模型
建构种群增长模型的方法
种群的“S”形增长
种群的“J”形增长
自然种群的数量变动
条件:食物和空间充裕、气候适宜、无天敌和其他竞争物种
特点:种群数量每年以一定倍数增长
一段时间内相对稳定(接近K值)
条件:食物和空间有限
特点:种群增长速率先增大后减小,最后为0
K值:一定环境条件下所能维持的种群最大数量
探究培养液中酵母菌种群数量变化(验证种群数量增长模型)
持续性的或急剧的下降,甚至衰退和消亡
规则或不规则波动。(K值是种群数量波动的平均值,波动中的生物,在某些特定条件下可能出现种群爆发)
小结
