2021-2022人教版八年级上册数学25.3用频率估计概率同步作业(Word版含答案)
文档属性
| 名称 | 2021-2022人教版八年级上册数学25.3用频率估计概率同步作业(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 215.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 00:00:00 | ||
图片预览


文档简介
人教版八年级上册数学25.3用频率估计概率同步作业
一、单选题
1.在一个不透明的袋子中有除颜色外均相同的6个白球和若干黑球,通过多次摸球试验后,发现摸到白球的频率约为30%,估计袋中黑球有( )个.
A.8 B.9 C.14 D.15
2.一个不透明的袋子中装有除颜色外完全相同的黑、白棋子若干,小明进行了大量的摸出棋子记录颜色后放回再摸的试验,发现摸出黑棋子的频率稳定在0.6附近,那么摸出白棋子的概率约是( )
A. B. C. D.
3.在一个不透明的布袋中装有50个红、白两种颜色的球,除颜色外其他都相同,小东通过多次摸球试验后发现,摸到红球的频率稳定在0.30左右,则布袋中红球可能有( )
A.13个 B.15个 C.25个 D.35个
4.在一个不透明的盒子中装有m个除颜色外完全相同的球,这m个球中只有4个红球.若每次将球充分搅匀后,任意摸出1个球记下颜色后再放回盒子.通过大量重复试验后,发现摸到红球的频率稳定在25%左右,则m的值大约为( )
A.10 B.12 C.16 D.20
5.已知数据:,,,,.其中无理数出现的频率为( )
A. B. C. D.
6.如图1所示,平整的地面上有一个不规则图案(图中阴影部分),小明想了解该图案的面积是多少,他采取了以下办法:用一个长为,宽为的长方形,将不规则图案围起来,然后在适当位置随机朝长方形区域扔小球,并记录小球落在不规则图案上的次数(小球扔在界线上或长方形区域外不计入试验结果),他将若干次有效试验的结果绘制成了图2所示的折线统计图,由此可估计不规则图案的面积大约是( )
A. B. C. D.
7.育种小组对某品种小麦发芽情况进行测试,在测试基本情况相同的条件下,得到如下数据:
抽查小麦粒数 100 500 1000 2000 3000 4000
发芽粒数 95 486 968 1940 2907
则的值最有可能是( )
A.3680 B.3720 C.3880 D.3960
8.甲、乙两名同学在一次用频率去估计概率的实验中,统计了某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是( )
A.抛一枚硬币,连续两次出现正面的概率
B.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
C.任意写一个正整数,它能被5整除的概率
D.掷一枚正六面体的骰子,出现1点的概率
二、填空题
9.在一个不透明的袋子中,有除颜色外完全相同的7个黑球、5个白球,若干个红球,每次摇匀后摸出一球,记下颜色后再放回袋中.通过大量重复摸球实验后,发现摸到红球的频率稳定在0.4,由此可估计袋中红球的个数为_______.
10.为了估计鱼塘中鱼的条数,养鱼者首先从鱼塘中打捞30条鱼做上标记,然后放回鱼塘,经过一段时间后,等有标记的鱼完全混合于鱼群中,再打捞200条鱼,发现其中带标记的鱼有3条,则鱼塘中鱼的条数估计有_____条.
11.一般地,当试验的可能结果有很多且各种可能结果发生的可能性相等时,则用列举法,利用概率公式__________的方式得出概率.
当试验的所有可能结果不是有限个,或各种可能结果发生的可能性不相等时,常常是通过______来估计概率,即在同样条件下,大量重复试验所得到的随机事件发生的频率的稳定值来估计这个事件发生的_______.
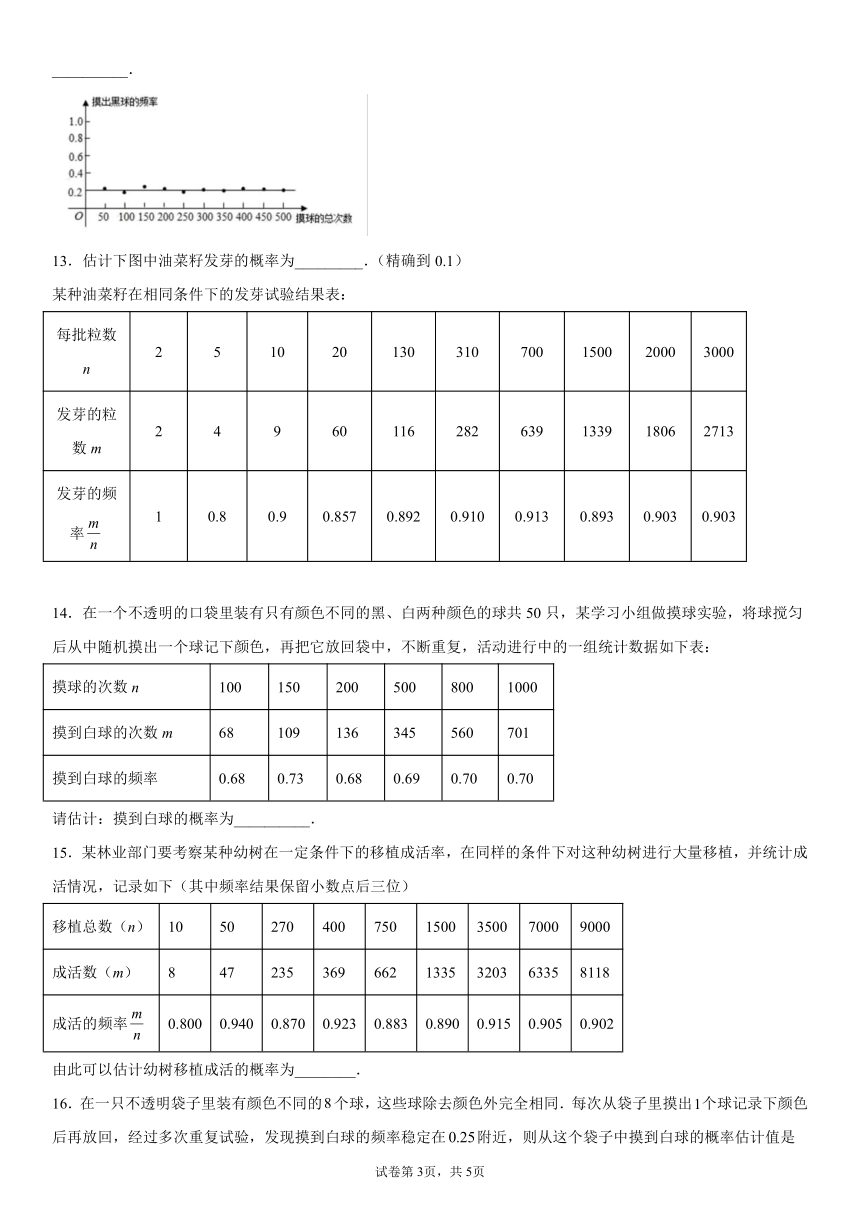
12.社团课上,同学们进行了“摸球游戏”在一个不透明的盒子里装有几十个除颜色不同外其余均相同的黑、白两种球,将盒子里面的球搅匀后从中随机摸一个球记下颜色,再把它放回盒子中,不断重复上述过程整理数据后,制作了“摸出黑球的频率”与“摸球的总次数”的关系图如图所示,经分析可以估计盒子里黑球与白球的个数比为__________.
13.估计下图中油菜籽发芽的概率为_________.(精确到0.1)
某种油菜籽在相同条件下的发芽试验结果表:
每批粒数n 2 5 10 20 130 310 700 1500 2000 3000
发芽的粒数m 2 4 9 60 116 282 639 1339 1806 2713
发芽的频率 1 0.8 0.9 0.857 0.892 0.910 0.913 0.893 0.903 0.903
14.在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共50只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,活动进行中的一组统计数据如下表:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 68 109 136 345 560 701
摸到白球的频率 0.68 0.73 0.68 0.69 0.70 0.70
请估计:摸到白球的概率为__________.
15.某林业部门要考察某种幼树在一定条件下的移植成活率,在同样的条件下对这种幼树进行大量移植,并统计成活情况,记录如下(其中频率结果保留小数点后三位)
移植总数(n) 10 50 270 400 750 1500 3500 7000 9000
成活数(m) 8 47 235 369 662 1335 3203 6335 8118
成活的频率 0.800 0.940 0.870 0.923 0.883 0.890 0.915 0.905 0.902
由此可以估计幼树移植成活的概率为________.
16.在一只不透明袋子里装有颜色不同的个球,这些球除去颜色外完全相同.每次从袋子里摸出个球记录下颜色后再放回,经过多次重复试验,发现摸到白球的频率稳定在附近,则从这个袋子中摸到白球的概率估计值是______.
三、解答题
17.在一个暗箱里放有a个除颜色外都完全相同的红、白、蓝三种球,其中红球有4个,白球有10个,每次将球搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球实验后发现,摸到红球的频率稳定在20%.
(1)试求出a的值;
(2)从中任意摸出一个球,下列事件:①该球是红球;②该球是白球;③该球是蓝球.试估计这三个事件发生的可能性的大小,并将三个事件按发生的可能性从小到大的顺序排列(用序号表示事件).
18.某射手在同一条件下进行射击,结果如下表所示:
射击次数(n) 10 20 50 100 200 500
击中靶心次数(m) 9 19 44 91 178 451
击中靶心频率()
(1)计算表中击中靶心的各个频率(精确到0.01);
(2)这个射手射击一次,击中靶心的概率约是多少(精确到0.1)?
19.你相信那些用摸彩来吸引人去碰“运气”的游戏吗?某人设摊“摸彩”,他手拿一个布袋,内装除颜色外完全相同的4个红球和4个绿球,每次让顾客“免费”从袋中摸出4个球,输赢的规则是:
所摸球的颜色 顾客的收益
4个全红 得50元
3红1绿 得20元
2红2绿 失30元
1红3绿 得20元
4个全绿 得50元
若你摸出了2红2绿则失30元,而对于其他四种情况,你均能赢钱.乍一看,此规则似乎对顾客有利,许多人都难免动心去碰碰“运气”,甚至有人连连试了数次.然而,顾客大多数都免不了以失败告终,而且试的次数越多,输的也就越多.假如5种情况是等可能的,则赢的机会为,输的机会仅为,平均每摸5次有4次都应该赢,但游戏的妙处就在于这5种情况的发生不是等可能的.经过计算可知,这5种情况出现的概率如下:
所摸球的颜色 出现的概率
4个全红
3红1绿
2红2绿
1红3绿
4个全绿
从表中可以看出,要想摸出“4个全红”或“4个全绿”的概率仅为,而摸到2红2绿的概率为,即有超过一半的机会失30元.
请你计算这种游戏中顾客每摸一次球的平均收益.
20.在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黄球6个.
(1)先从袋子中取出个红球(且为正整数),再从袋子中随机摸一个小球,将“摸出黄球”记为事件A.
①若事件为必然事件,则的值为______;
②若事件为随机事件,则的值为______.
(2)先从袋子中取出个红球,再放入个一样的黄球并摇匀,经过多次试验,随机摸出一个黄球的频率在附近摆动,求的值.
参考答案
1.C
2.B
3.B
4.C
5.B
6.B
7.C
8.B
9.8
10.2000
11.P(A)= 统计频率 概率
12.1:4
13.0.9
14.
15.0.892
16.0.25
17.(1)20;(2)①③②.
18.(1)击中靶心的各个频率依次是:0.90,0.95,0.88,0.91,0.89,0.90;(2) 0.9.
19.元
20.(1)①4;②2或3;(2)
试卷第4页,共5页
试卷第5页,共5页
一、单选题
1.在一个不透明的袋子中有除颜色外均相同的6个白球和若干黑球,通过多次摸球试验后,发现摸到白球的频率约为30%,估计袋中黑球有( )个.
A.8 B.9 C.14 D.15
2.一个不透明的袋子中装有除颜色外完全相同的黑、白棋子若干,小明进行了大量的摸出棋子记录颜色后放回再摸的试验,发现摸出黑棋子的频率稳定在0.6附近,那么摸出白棋子的概率约是( )
A. B. C. D.
3.在一个不透明的布袋中装有50个红、白两种颜色的球,除颜色外其他都相同,小东通过多次摸球试验后发现,摸到红球的频率稳定在0.30左右,则布袋中红球可能有( )
A.13个 B.15个 C.25个 D.35个
4.在一个不透明的盒子中装有m个除颜色外完全相同的球,这m个球中只有4个红球.若每次将球充分搅匀后,任意摸出1个球记下颜色后再放回盒子.通过大量重复试验后,发现摸到红球的频率稳定在25%左右,则m的值大约为( )
A.10 B.12 C.16 D.20
5.已知数据:,,,,.其中无理数出现的频率为( )
A. B. C. D.
6.如图1所示,平整的地面上有一个不规则图案(图中阴影部分),小明想了解该图案的面积是多少,他采取了以下办法:用一个长为,宽为的长方形,将不规则图案围起来,然后在适当位置随机朝长方形区域扔小球,并记录小球落在不规则图案上的次数(小球扔在界线上或长方形区域外不计入试验结果),他将若干次有效试验的结果绘制成了图2所示的折线统计图,由此可估计不规则图案的面积大约是( )
A. B. C. D.
7.育种小组对某品种小麦发芽情况进行测试,在测试基本情况相同的条件下,得到如下数据:
抽查小麦粒数 100 500 1000 2000 3000 4000
发芽粒数 95 486 968 1940 2907
则的值最有可能是( )
A.3680 B.3720 C.3880 D.3960
8.甲、乙两名同学在一次用频率去估计概率的实验中,统计了某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是( )
A.抛一枚硬币,连续两次出现正面的概率
B.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
C.任意写一个正整数,它能被5整除的概率
D.掷一枚正六面体的骰子,出现1点的概率
二、填空题
9.在一个不透明的袋子中,有除颜色外完全相同的7个黑球、5个白球,若干个红球,每次摇匀后摸出一球,记下颜色后再放回袋中.通过大量重复摸球实验后,发现摸到红球的频率稳定在0.4,由此可估计袋中红球的个数为_______.
10.为了估计鱼塘中鱼的条数,养鱼者首先从鱼塘中打捞30条鱼做上标记,然后放回鱼塘,经过一段时间后,等有标记的鱼完全混合于鱼群中,再打捞200条鱼,发现其中带标记的鱼有3条,则鱼塘中鱼的条数估计有_____条.
11.一般地,当试验的可能结果有很多且各种可能结果发生的可能性相等时,则用列举法,利用概率公式__________的方式得出概率.
当试验的所有可能结果不是有限个,或各种可能结果发生的可能性不相等时,常常是通过______来估计概率,即在同样条件下,大量重复试验所得到的随机事件发生的频率的稳定值来估计这个事件发生的_______.
12.社团课上,同学们进行了“摸球游戏”在一个不透明的盒子里装有几十个除颜色不同外其余均相同的黑、白两种球,将盒子里面的球搅匀后从中随机摸一个球记下颜色,再把它放回盒子中,不断重复上述过程整理数据后,制作了“摸出黑球的频率”与“摸球的总次数”的关系图如图所示,经分析可以估计盒子里黑球与白球的个数比为__________.
13.估计下图中油菜籽发芽的概率为_________.(精确到0.1)
某种油菜籽在相同条件下的发芽试验结果表:
每批粒数n 2 5 10 20 130 310 700 1500 2000 3000
发芽的粒数m 2 4 9 60 116 282 639 1339 1806 2713
发芽的频率 1 0.8 0.9 0.857 0.892 0.910 0.913 0.893 0.903 0.903
14.在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共50只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,活动进行中的一组统计数据如下表:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 68 109 136 345 560 701
摸到白球的频率 0.68 0.73 0.68 0.69 0.70 0.70
请估计:摸到白球的概率为__________.
15.某林业部门要考察某种幼树在一定条件下的移植成活率,在同样的条件下对这种幼树进行大量移植,并统计成活情况,记录如下(其中频率结果保留小数点后三位)
移植总数(n) 10 50 270 400 750 1500 3500 7000 9000
成活数(m) 8 47 235 369 662 1335 3203 6335 8118
成活的频率 0.800 0.940 0.870 0.923 0.883 0.890 0.915 0.905 0.902
由此可以估计幼树移植成活的概率为________.
16.在一只不透明袋子里装有颜色不同的个球,这些球除去颜色外完全相同.每次从袋子里摸出个球记录下颜色后再放回,经过多次重复试验,发现摸到白球的频率稳定在附近,则从这个袋子中摸到白球的概率估计值是______.
三、解答题
17.在一个暗箱里放有a个除颜色外都完全相同的红、白、蓝三种球,其中红球有4个,白球有10个,每次将球搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球实验后发现,摸到红球的频率稳定在20%.
(1)试求出a的值;
(2)从中任意摸出一个球,下列事件:①该球是红球;②该球是白球;③该球是蓝球.试估计这三个事件发生的可能性的大小,并将三个事件按发生的可能性从小到大的顺序排列(用序号表示事件).
18.某射手在同一条件下进行射击,结果如下表所示:
射击次数(n) 10 20 50 100 200 500
击中靶心次数(m) 9 19 44 91 178 451
击中靶心频率()
(1)计算表中击中靶心的各个频率(精确到0.01);
(2)这个射手射击一次,击中靶心的概率约是多少(精确到0.1)?
19.你相信那些用摸彩来吸引人去碰“运气”的游戏吗?某人设摊“摸彩”,他手拿一个布袋,内装除颜色外完全相同的4个红球和4个绿球,每次让顾客“免费”从袋中摸出4个球,输赢的规则是:
所摸球的颜色 顾客的收益
4个全红 得50元
3红1绿 得20元
2红2绿 失30元
1红3绿 得20元
4个全绿 得50元
若你摸出了2红2绿则失30元,而对于其他四种情况,你均能赢钱.乍一看,此规则似乎对顾客有利,许多人都难免动心去碰碰“运气”,甚至有人连连试了数次.然而,顾客大多数都免不了以失败告终,而且试的次数越多,输的也就越多.假如5种情况是等可能的,则赢的机会为,输的机会仅为,平均每摸5次有4次都应该赢,但游戏的妙处就在于这5种情况的发生不是等可能的.经过计算可知,这5种情况出现的概率如下:
所摸球的颜色 出现的概率
4个全红
3红1绿
2红2绿
1红3绿
4个全绿
从表中可以看出,要想摸出“4个全红”或“4个全绿”的概率仅为,而摸到2红2绿的概率为,即有超过一半的机会失30元.
请你计算这种游戏中顾客每摸一次球的平均收益.
20.在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黄球6个.
(1)先从袋子中取出个红球(且为正整数),再从袋子中随机摸一个小球,将“摸出黄球”记为事件A.
①若事件为必然事件,则的值为______;
②若事件为随机事件,则的值为______.
(2)先从袋子中取出个红球,再放入个一样的黄球并摇匀,经过多次试验,随机摸出一个黄球的频率在附近摆动,求的值.
参考答案
1.C
2.B
3.B
4.C
5.B
6.B
7.C
8.B
9.8
10.2000
11.P(A)= 统计频率 概率
12.1:4
13.0.9
14.
15.0.892
16.0.25
17.(1)20;(2)①③②.
18.(1)击中靶心的各个频率依次是:0.90,0.95,0.88,0.91,0.89,0.90;(2) 0.9.
19.元
20.(1)①4;②2或3;(2)
试卷第4页,共5页
试卷第5页,共5页
同课章节目录
