2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册2.5.2圆与圆的位置关系教学 课件(共28张PPT)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册2.5.2圆与圆的位置关系教学 课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-28 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
2.5.2圆与圆的位置关系
二、探究典例,初步应用
三、具体感知,理性分析
四、初步应用,理解概念
一、创设情境,引发思考
五、归纳小结,课后作业
创设情境,引发思考
【实际情境】
每逢节假日农村集市上出现各式各样套圈活动,套硬币更是博人眼球,商家圈起来一小片空地,撒满一元,五角和一角的硬币,玩家花10元钱可套30环,看似简单套起来却没有那么容易,要求套环落地后不触碰硬币,毕竟硬币面值越大,想套中就越难。
一、创设情境,引发思考
问题1:
(1)每次套圈时把目标硬币和套环看成两个圆,那么这两个圆满足什么位置关系才算套中?
(2)为什么硬币面值越大,想套中就越难?
(3)两个圆的位置关系和圆心距以及半径存在怎样的数量关系?
【数学情境】
尺规作图,请同学们在纸上分别画出半径为 和 的圆,以小组为单位进行汇总,看看可以画出多少种位置关系,并探讨不同位置关系的圆心距满足的条件,由特殊到一般,归纳任意两圆位置关系及满足条件.
位置关系
图示
圆心距与半径的关系
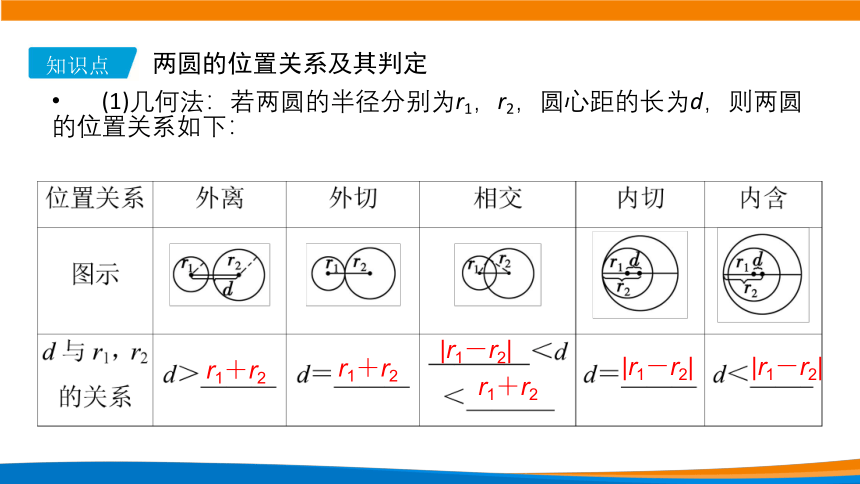
(1)几何法:若两圆的半径分别为r1,r2,圆心距的长为d,则两圆的位置关系如下:
知识点
两圆的位置关系及其判定
r1+r2
r1+r2
|r1-r2|
r1+r2
|r1-r2|
|r1-r2|
知识点
问题2:如果建立平面直角坐标系,把目标硬币和套环看成两个圆,得到两个圆的方程,类比直线与圆的位置关系,是否可以根据方程组解的个数,来判断两个圆的位置关系?
则方程组解的个数与两圆的位置关系如下:
方程组解的个数 2组 1组 0组
两圆的公共点个数 2个 1个 0个
两圆的位置关系 ________ ______________ ______________
相交
外切或内切
外离或内含
知识点
知识点
探究典例,初步应用
活动 判断两圆的位置关系
已知圆C1:x2+y2-2ax-2y+a2-15=0(a>0),
圆C2:x2+y2-4ax-2y+4a2=0(a>0).试求a为何值时,
两圆C1,C2的位置关系为: (1)相切;(2)相交;(3)外离;(4)内含?
【分析】 先求出圆心距,与两半径的和或差比较求出a的值.
题型探究
(1)当|C1C2|=r1+r2=5,即a=5时,两圆外切;
(2)当|C1C2|=r1-r2=3,即a=3时,两圆内切.
(3)当3<|C1C2|<5,即3<a<5时,两圆相交.
(4)当|C1C2|>5,即a>5时,两圆外离.
(5)当|C1C2|<3,即0<a<3时,两圆内含.
【规律方法】判断两圆的位置关系的两种方法
(1)几何法:利用两圆半径的和或差与圆心距作比较,得到两圆的位置关系.
(2)代数法:把两圆位置关系的判定完全转化为代数问题,转化为方程组的解的组数问题.
具体感知,理性分析
已知圆C1: ,圆C2: ,试判断圆C1与圆C2的位置关系.
解法1:将圆C1与圆C2的方程联立,得到方程组
①-②,得
③
活动 判断两圆的位置关系
①
②
将上式代入①,并整理,得 ④
方程④的根的判别式
所以这两个圆相交.
圆C2的圆心为(2,2),半径r2= .
解法2:把圆C1的方程化为标准方程,得
圆C1的圆心为(-1,-4),半径r1=5.
把圆C2的方程化为标准方程,得
圆C1与圆C2的连心线的长为
圆C1与圆C2的两半径之和 ,两半径长之差
所以圆C1与圆C2相交.
问题3: 如果两圆方程联立消元后得到的方程的 ,它说明什么?你能据此确定两圆是内切还是外切吗?如何判断两圆是内切还是外切呢?
如果 ,则两圆相切;
此时无法判定两圆是内切还
是外切,
还要根据两圆的半径与连心线的长作进一步判断.
如果 ,则两圆相离,包括外离和内含.
问题4:画出圆C1与圆C2以及方程③表示的直线,你发现了什么?并求出圆C1与圆C2的交点坐标.
③
A
B
解:两相交圆方程相减得公共弦方程
将 式代入①,并整理,得 ④
③
解得:x1=-1,x2=3.
得 y1=1,y2=-1.
点A(-1,1),B(3,-1).
初步应用,理解概念
例1(2021·皖南八校联考)已知圆 的方程为 , 圆 的方程为 ,如果这两个圆有且只有一个公共点,那么a的所有取值构成的集合是( )
A.{1,-1} B.{3,-3}
C.{1,-1,3,-3} D.{5,-5,3,-3}
C
解析: 两圆只有1个公共点,则两圆外切或内切.
如果两圆外切,则|a|=2+1=3,a=±3;
如果两圆内切,则|a|=1,a=±1.
综上,a∈{1,-1,3,-3},选C.
A.(1,0)和(0,1) B.(1,0)和(0,-1)
C. (-1,0)和(0,-1) D.(-1,0)和(0,1)
C
例3:已知两圆x2+y2-2x+10y-24=0和x2+y2+2x+2y-8=0,求公共弦的长度.
【解析】以 的中点 为原点, 所在的直线为x轴,建立如图所示的平面直角坐标系,则 由已知|PM|= |PN|, 得|PM|2=2|PN|2.因为两圆的半径长均为1, 所以|PO1|2-1=2(|PO2|2-1).
设P(x,y),则(x+2)2+y2-1=2[(x-2)2+y2-1],
化简,得(x-6)2+y2=33,
所以所求轨迹方程为(x-6)2+y2=33.
归纳小结,课后作业
1.判断圆与圆的位置关系的两种方法:几何法和代数法
3.满足某种几何条件的动点圆的轨迹问题,用的是坐标法.这种方法建立了几何与代数之间的联系,体现了数形结合思想.
2.求两个相交圆公共弦长的两种方法:几何法和代数法
归纳小结
课后作业
1.教科书130页练习;习题4.2 A组第4、9、10、11题.
2.步步高《圆与圆位置关系》相应习题
再会!
2.5.2圆与圆的位置关系
二、探究典例,初步应用
三、具体感知,理性分析
四、初步应用,理解概念
一、创设情境,引发思考
五、归纳小结,课后作业
创设情境,引发思考
【实际情境】
每逢节假日农村集市上出现各式各样套圈活动,套硬币更是博人眼球,商家圈起来一小片空地,撒满一元,五角和一角的硬币,玩家花10元钱可套30环,看似简单套起来却没有那么容易,要求套环落地后不触碰硬币,毕竟硬币面值越大,想套中就越难。
一、创设情境,引发思考
问题1:
(1)每次套圈时把目标硬币和套环看成两个圆,那么这两个圆满足什么位置关系才算套中?
(2)为什么硬币面值越大,想套中就越难?
(3)两个圆的位置关系和圆心距以及半径存在怎样的数量关系?
【数学情境】
尺规作图,请同学们在纸上分别画出半径为 和 的圆,以小组为单位进行汇总,看看可以画出多少种位置关系,并探讨不同位置关系的圆心距满足的条件,由特殊到一般,归纳任意两圆位置关系及满足条件.
位置关系
图示
圆心距与半径的关系
(1)几何法:若两圆的半径分别为r1,r2,圆心距的长为d,则两圆的位置关系如下:
知识点
两圆的位置关系及其判定
r1+r2
r1+r2
|r1-r2|
r1+r2
|r1-r2|
|r1-r2|
知识点
问题2:如果建立平面直角坐标系,把目标硬币和套环看成两个圆,得到两个圆的方程,类比直线与圆的位置关系,是否可以根据方程组解的个数,来判断两个圆的位置关系?
则方程组解的个数与两圆的位置关系如下:
方程组解的个数 2组 1组 0组
两圆的公共点个数 2个 1个 0个
两圆的位置关系 ________ ______________ ______________
相交
外切或内切
外离或内含
知识点
知识点
探究典例,初步应用
活动 判断两圆的位置关系
已知圆C1:x2+y2-2ax-2y+a2-15=0(a>0),
圆C2:x2+y2-4ax-2y+4a2=0(a>0).试求a为何值时,
两圆C1,C2的位置关系为: (1)相切;(2)相交;(3)外离;(4)内含?
【分析】 先求出圆心距,与两半径的和或差比较求出a的值.
题型探究
(1)当|C1C2|=r1+r2=5,即a=5时,两圆外切;
(2)当|C1C2|=r1-r2=3,即a=3时,两圆内切.
(3)当3<|C1C2|<5,即3<a<5时,两圆相交.
(4)当|C1C2|>5,即a>5时,两圆外离.
(5)当|C1C2|<3,即0<a<3时,两圆内含.
【规律方法】判断两圆的位置关系的两种方法
(1)几何法:利用两圆半径的和或差与圆心距作比较,得到两圆的位置关系.
(2)代数法:把两圆位置关系的判定完全转化为代数问题,转化为方程组的解的组数问题.
具体感知,理性分析
已知圆C1: ,圆C2: ,试判断圆C1与圆C2的位置关系.
解法1:将圆C1与圆C2的方程联立,得到方程组
①-②,得
③
活动 判断两圆的位置关系
①
②
将上式代入①,并整理,得 ④
方程④的根的判别式
所以这两个圆相交.
圆C2的圆心为(2,2),半径r2= .
解法2:把圆C1的方程化为标准方程,得
圆C1的圆心为(-1,-4),半径r1=5.
把圆C2的方程化为标准方程,得
圆C1与圆C2的连心线的长为
圆C1与圆C2的两半径之和 ,两半径长之差
所以圆C1与圆C2相交.
问题3: 如果两圆方程联立消元后得到的方程的 ,它说明什么?你能据此确定两圆是内切还是外切吗?如何判断两圆是内切还是外切呢?
如果 ,则两圆相切;
此时无法判定两圆是内切还
是外切,
还要根据两圆的半径与连心线的长作进一步判断.
如果 ,则两圆相离,包括外离和内含.
问题4:画出圆C1与圆C2以及方程③表示的直线,你发现了什么?并求出圆C1与圆C2的交点坐标.
③
A
B
解:两相交圆方程相减得公共弦方程
将 式代入①,并整理,得 ④
③
解得:x1=-1,x2=3.
得 y1=1,y2=-1.
点A(-1,1),B(3,-1).
初步应用,理解概念
例1(2021·皖南八校联考)已知圆 的方程为 , 圆 的方程为 ,如果这两个圆有且只有一个公共点,那么a的所有取值构成的集合是( )
A.{1,-1} B.{3,-3}
C.{1,-1,3,-3} D.{5,-5,3,-3}
C
解析: 两圆只有1个公共点,则两圆外切或内切.
如果两圆外切,则|a|=2+1=3,a=±3;
如果两圆内切,则|a|=1,a=±1.
综上,a∈{1,-1,3,-3},选C.
A.(1,0)和(0,1) B.(1,0)和(0,-1)
C. (-1,0)和(0,-1) D.(-1,0)和(0,1)
C
例3:已知两圆x2+y2-2x+10y-24=0和x2+y2+2x+2y-8=0,求公共弦的长度.
【解析】以 的中点 为原点, 所在的直线为x轴,建立如图所示的平面直角坐标系,则 由已知|PM|= |PN|, 得|PM|2=2|PN|2.因为两圆的半径长均为1, 所以|PO1|2-1=2(|PO2|2-1).
设P(x,y),则(x+2)2+y2-1=2[(x-2)2+y2-1],
化简,得(x-6)2+y2=33,
所以所求轨迹方程为(x-6)2+y2=33.
归纳小结,课后作业
1.判断圆与圆的位置关系的两种方法:几何法和代数法
3.满足某种几何条件的动点圆的轨迹问题,用的是坐标法.这种方法建立了几何与代数之间的联系,体现了数形结合思想.
2.求两个相交圆公共弦长的两种方法:几何法和代数法
归纳小结
课后作业
1.教科书130页练习;习题4.2 A组第4、9、10、11题.
2.步步高《圆与圆位置关系》相应习题
再会!
