2021-2022学年北师大版九年级数学下册2.3确定二次函数表达式同步训练(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册2.3确定二次函数表达式同步训练(Word版,附答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 306.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览




文档简介
2021-2022学年北师大版九年级数学下册《2.3确定二次函数表达式》培优训练(附答案)
1.函数写成y=a(x﹣h)2+k的形式是( )
A. B.
C. D.
2.已知抛物线与二次函数y=2x2的图象的开口大小相同,开口方向相反,且顶点坐标为(﹣1,2021),则该抛物线对应的函数表达式为( )
A.y=﹣2(x﹣1)2+2021 B.y=2(x﹣1)2+2021
C.y=2(x+1)2+2021 D.y=﹣2(x+1)2+2021
3.如图是一个不倒翁的部分剖面图,可看作一个抛物线,若肚子最大的宽度AB=10cm,OD=15cm,按图示位置建立的平面直角坐标系可知,抛物线表达式为( )
A.y=x2 B.y=﹣x2 C.y=x2 D.y=﹣x2
4.已知二次函数的图象如图所示,那么此函数的解析式只可能是( )
A.y=﹣x2+x+3 B.y=﹣x2﹣3x﹣3 C.y=﹣x2﹣x+3 D.y=x2+x+3
5.顶点为(﹣6,0),开口向下,形状与函数y=x2的图象相同的抛物线的表达式是 .
6.已知抛物线与x轴交点的横坐标分别为3,1;与y轴交点的纵坐标为6,则二次函数的关系式是 .
7.在平面直角坐标系中,抛物线y=ax2+bx+c的顶点为A,且经过平行四边形ABCD的顶点A,B(1,m),D(7,1),它的对称轴经过AC,BD的交点,若AB=5,则这条抛物线的解析式为 .
8.已知某抛物线的顶点为(2,4),且过点(1,2).
(1)求抛物线的解析式;
(2)动点P(a,6)能否在抛物线上?请说明理由;
(3)若点A(m,y1),B(n,y2)都在抛物线上,且m<n<0,比较y1,y2的大小,并说明理由.
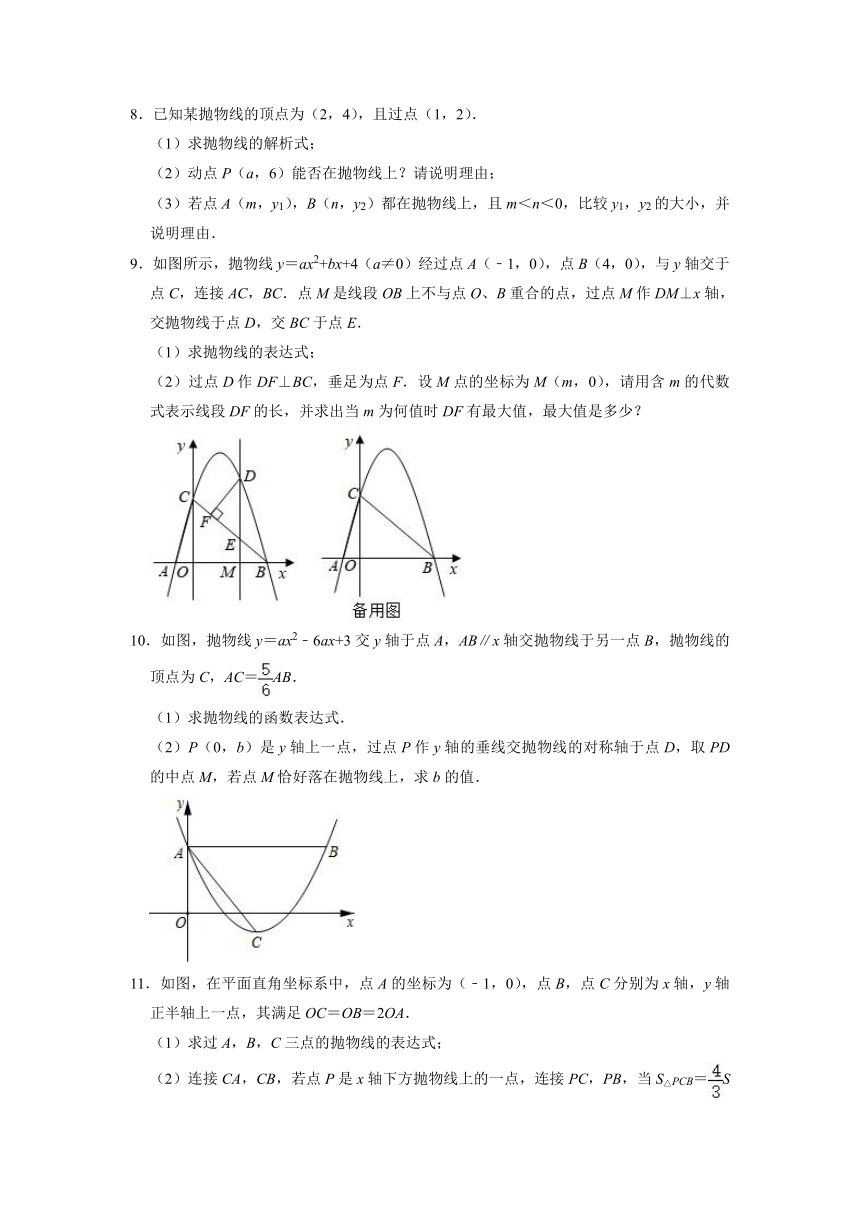
9.如图所示,抛物线y=ax2+bx+4(a≠0)经过点A(﹣1,0),点B(4,0),与y轴交于点C,连接AC,BC.点M是线段OB上不与点O、B重合的点,过点M作DM⊥x轴,交抛物线于点D,交BC于点E.
(1)求抛物线的表达式;
(2)过点D作DF⊥BC,垂足为点F.设M点的坐标为M(m,0),请用含m的代数式表示线段DF的长,并求出当m为何值时DF有最大值,最大值是多少?
10.如图,抛物线y=ax2﹣6ax+3交y轴于点A,AB∥x轴交抛物线于另一点B,抛物线的顶点为C,AC=AB.
(1)求抛物线的函数表达式.
(2)P(0,b)是y轴上一点,过点P作y轴的垂线交抛物线的对称轴于点D,取PD的中点M,若点M恰好落在抛物线上,求b的值.
11.如图,在平面直角坐标系中,点A的坐标为(﹣1,0),点B,点C分别为x轴,y轴正半轴上一点,其满足OC=OB=2OA.
(1)求过A,B,C三点的抛物线的表达式;
(2)连接CA,CB,若点P是x轴下方抛物线上的一点,连接PC,PB,当S△PCB=S△ACB时,求点P的坐标.
12.已知抛物线y=ax2+2ax+5﹣a2经过点(﹣3,﹣5).
(1)求该抛物线的表达式及顶点坐标.
(2)设点A(m,y1),B(1,y2)在抛物线上,若y1>y2,求m的取值范围.
13.如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0)
(1)求抛物线的解析式和顶点E坐标;
(2)该抛物线有一点D,使得S△DBC=S△EBC,求点D的坐标.
14.如图,抛物线的顶点为A(﹣3,﹣3),此抛物线交x轴于O、B两点.
(1)求此抛物线的解析式;
(2)求△AOB的面积;
(3)若抛物线上另一点P满足S△POB=S△AOB,请求出点P的坐标.
15.如图,已知抛物线的顶点为A(0,1),矩形CDEF的顶点C、F在抛物线上,点D、E在x轴上,CF交y轴于点B(0,2),且矩形面积为8.
(1)求此抛物线的解析式;
(2)求当﹣1≤x≤3时,y的取值范围;
(3)直接写出当y>3时,x的取值范围.
16.如图,在平面直角坐标系中,∠AOB=90°,AO=BO,点A的坐标为(﹣1,3).
(1)求点B的坐标;
(2)抛物线y=ax2+bx经过点A、B,求它的解析式.
17.平面直角坐标系中,函数y=x2﹣2ax﹣1(a为常数)的图象与y轴交于点A.
(1)直接写出A点坐标;
(2)当此函数图象经过点(1,2)时,求此函数表达式,并写出函数y随x增大而增大时x的取值范围;
(3)当x≥0时,若函数y=x2﹣2ax﹣1(a为常数)图象最低点到直线y=2a的距离为3,求a的值.
18.如图,两条抛物线y1=﹣x2+4,y2=﹣x2+bx+c相交于A,B两点,点A在x轴负半轴上,且为抛物线y2的最高点.
(1)求抛物线y2的解析式和点B的坐标;
(2)点C是抛物线y1上A,B之间的一点,过点C作x轴的垂线交y2于点D,当线段CD取最大值时,求S△BCD.
19.如图,在平面坐标系xOy中,点A的坐标为(1,0),点P的横坐标为2,将点A绕点P旋转,使它的对应点B恰好落在x轴上(不与A点重合);再将点B绕点O逆时针旋转90°得到点C.
(1)直接写出点B和点C的坐标;
(2)求经过A,B,C三点的抛物线的表达式.
参考答案
1.解:=﹣(x2﹣6x+9﹣9)﹣2=(x﹣3)2+1,即y=(x﹣1)2+.
故选:D.
2.解:∵抛物线的顶点坐标为(﹣1,2021),
∴抛物线的解析式为y=a(x+1)2+2021,
∵抛物线y=a(x+1)2+2021二次函数y=2x2的图象的开口大小相同,开口方向相反,
∴a=﹣2,
∴抛物线的解析式为y=﹣2(x+1)2+2021.
故选:D.
3.解:由题意可知A(﹣5,15),B(5,15),顶点是原点,
设抛物线的解析式为y=ax2,
∴15=25a,
解得a=,
∴抛物线表达式为y=x2,
故选:A.
4.解:∵抛物线开口向下,
∴a<0,
∵对称轴在y轴的左侧,
∴a、b同号,
∴b<0,
∵抛物线交y轴的正半轴,
∴c>0.
故选:C.
5.解:设所求的抛物线的关系式为y=a(x﹣h)2+k,
∵顶点为(﹣6,0),
∴h=﹣6,k=0,
又∵开口向下,形状与函数y=x2的图象相同,
∴a=﹣,
∴抛物线的关系式为:y=﹣(x+6)2,
6.解:设所求抛物线是y=ax2+bx+c,根据题意得,
,
解得
,
故所求函数解析式是y=2x2﹣8x+6.
故答案是y=2x2﹣8x+6.
7.解:设抛物线的解析式为y=ax2+bx+c(a≠0),
因为四边形ABCD是平行四边形,
所以AC,BD互相平分且O'为AC,BD的中点,
又因为B(1,m),D(7,1),
所以,
所以抛物线对称轴为直线x=4,
过点A作AE⊥直线x=1于点E,
因为AE=3,AB=5,由勾股定理可得“,
又因为B(1,m),所以A(4,m﹣4)或(4,m+4),
因为B在抛物线上,所以B(1,a+b+c),A(4,a+b+c﹣4)或(4,a+b+c+4),
根据抛物线经过点D(7,1),A(4,a+b+c﹣4)或(4,a+b+c+4)且对称轴为直线x=4可列方程为:
或,
解得:或.
故抛物线的解析式为:或y=﹣+﹣.
8.解:(1)设抛物线的解析式为y=a(x﹣2)2+4,
将(1,2)代入上式得2=a(1﹣2)2+4,
解得a=﹣2,
∴抛物线的解析式为y=﹣2(x﹣2)2+4,
(2)动点P(a,6)不在抛物线上,理由如下:
∵抛物线y=﹣2(x﹣2)2+4的最大值为4,
∴动点P(a,6)不在抛物线上;
(3)∵抛物线的函数关系式为:y=﹣2(x﹣2)2+4,
∴抛物线的开口向下,对称轴为直线x=2,
∴当x<2时,y随x的增大而增大,
∵点A(m,y1),B(n,y2)都在抛物线上,且m<n<0<2,
∴y1<y2.
9.解:(1)A(﹣1,0),B(4,0)分别代入y=ax2+bx+4(a≠0)得,
解得:,
∴抛物线的表达式为:y=﹣x2+3x+4;
(2)把x=0代入y=﹣x2+3x+4得y=4,
∴C(0,4),
设BC所在直线解析式为y=kx+b,
把B(4,0),C(0,4)代入y=kx+b得:
,
解得,
∴y=﹣x+4,
设M(m,0),则D(m,﹣m2+3m+4),E(m,﹣m+4),
∴DE=﹣m2+3m+4+m﹣4=﹣m2+4m,
∵OB=OC=4,OC⊥OB,
∴∠OBC=∠OCB=45°,
∵DM⊥x轴,
∴∠DEF=∠BEM=45°,
又∵DF⊥BC,
∴DF=DE=(﹣m2+4m)=(m﹣2)2+2,
∵<0,
∴当m=2时,DF有最大值为2.
10.解:(1)抛物线y=ax2﹣6ax+3交y轴于点A,
令x=0,则y=3,
∴点A(0,3),
对称轴为:x=﹣=3,
∵AB∥x轴,
∴A、B关于x=3对称,
∴B(6,3),则AB=6,
又AC=AB=5,
过C作AB的垂线CN,
则AN=3,
在Rt△ACN中,
由勾股定理得:CN===4,
∴C(3,﹣1),
把C点坐标代入y=ax2﹣6ax+3得,
﹣1=9a﹣18a+3,
解得:a=,
∴抛物线函数表达式为:y=x2﹣x+3.
(2)由题意得:D点坐标为(3,b),
∵M为PD中点,
∴M(,b),
又∵M在抛物线上,代入得:
b=×﹣×+3=0,
∴b=0.
11.解:(1)∵点A的坐标为(﹣1,0),OC=OB=2OA.
∴B(2,0),C(0,2),
设过A、B、C三点的抛物线的解析式为y=a(x﹣2)(x+1),
把点C(0,2)代入,解得:a=﹣1,
所以抛物线的解析式为:y=﹣(x﹣2)(x+1)=﹣x2+x+2;
(2)如图,
∵S△ACB=AB OC=×3×2=3,
∴S△PCB=S△ACB=4,
∵点P是x轴下方抛物线上的一点,设P(m,﹣m2+m+2),
∴直线PC为y=(﹣m+1)x+2,y=0时,x=,m<﹣1或m>2,
∴S△PCB=BM [2﹣(﹣m2+m+2)]=×(2﹣)×(m2﹣m)=4,
解得:m=1﹣,
∴点P的坐标为(1+,﹣3﹣)或(1﹣,﹣3).
12.解:(1)∵抛物线y=ax2+2ax+5﹣a2经过点(﹣3,﹣5),
∴﹣5=9a﹣6a+5﹣a2,
解得a1=﹣2,a2=5,
当a=﹣2时,该抛物线的表达式是y=﹣2x2﹣4x+1=﹣2(x+1)2+3,顶点坐标为(﹣1,3),
当a=5时,该抛物线的表达式是y=5x2+10x﹣20=5(x+1)2﹣25,顶点坐标为(﹣1,﹣25),
由上可得,当a=﹣2时,该抛物线的表达式是y=﹣2x2﹣4x+1,顶点坐标为(﹣1,3);
当a=5时,该抛物线的表达式是y=5x2+10x﹣20,顶点坐标为(﹣1,﹣25);
(2)∵点A(m,y1),B(1,y2)在抛物线上,y1>y2,
∴当a=﹣2时,抛物线的表达式是y=﹣2x2﹣4x+1,顶点坐标为(﹣1,3),则﹣3<m<1;
当a=5时,该抛物线的表达式是y=5x2+10x﹣20,顶点坐标为(﹣1,﹣25),则m>1或m<﹣3.
13.解:(1)由题意,设y=a(x﹣1)(x﹣5),
代入A(0,4),得,
∴,
∴,
故顶点E坐标为;
(2)∵S△DBC=S△EBC,
∴两个三角形在公共边BC上的高相等,
又点E到BC的距离为,
∴点D到BC的距离也为,
则(x﹣3)2﹣=,
解得x=3±2,
则点D或.
14.解:(1)如图,连接AB、OA.设抛物线的解析式为y=a(x+3)2﹣3,
把(0,0)代入得a×32﹣3=0,解得a=,
所以此抛物线的解析式为y=(x+3)2﹣3;
(2)∵抛物线的对称轴为直线x=﹣3,
∴B点坐标为(﹣6,0),
∴△AOB的面积=×6×3=9;
(3)设P点坐标为(x,y),
∵S△POB=S△AOB,
∴|y|×6=9,
解得y=3或y=﹣3(舍去),
∴(x+3)2﹣3=3,
解得x1=3﹣3,x2=﹣3﹣3,
∴P点坐标为(3﹣3,3),(﹣3﹣3,3).
15.解:(1)∵A(0,1)为抛物线顶点,
∴抛物线对称轴为y轴,
∵C,F在抛物线上,
∴BC=BF,
∵矩形CDEF面积为CF OB=8,
∴CF==4,
∴BC=BF=2,
∴点F坐标为(2,2),
设抛物线解析式为y=ax2+1,
把(2,2)代入解析式得2=4a+1,
解得a=,
∴抛物线解析式为y=x2+1.
(2)∵抛物线开口向上,对称轴为y轴,
∴当x=0时,y取最小值为1,
∵3﹣0>0﹣(﹣1),
∴x=3时y取最大值,
把x=3代入y=x2+1得.
∴1≤y≤.
(3)把y=3代入y=x2+1得3=x2+1,
解得x=﹣2或x=2,
∴y>3时,x<﹣2或x>2.
16.解:(1)作AC⊥x轴于点C,BD⊥x轴于点D.
∴∠ACO=∠BDO=90°,∠AOC+∠CAO=90°.
∵∠AOB=90°,
∴∠AOC+∠BOD=90°.
∴∠CAO=∠BOD.
又∵AO=BO,
∴△AOC≌△OBD(AAS).
又∵A(﹣1,3),
∴AC=OD=3,OC=BD=1,
∴B(3,1).
(2)由抛物线y=ax2+bx经过点A(﹣1,3)、B(3,1)得,
解得,
∴解析式为.
17.解:(1)当x=0时,y=x2﹣2ax﹣1=﹣1,
∴点A的坐标为:(0,﹣1);
(2)将点(1,2)代入y=x2﹣2ax﹣1,
得:2=1﹣2a﹣1,
解得:a=﹣1,
∴函数的表达式为:y=x2+2x﹣1,
∵y=x2+2x﹣1=(x+1)2﹣2,
∴抛物线的开口向上,对称轴为直线x=﹣1,
∴当x≥﹣1时,y随x的增大而增大;
(3)抛物线y=x2﹣2ax﹣1=(x﹣a)2﹣a2﹣1的对称轴为:x=a,顶点坐标为:(a,﹣a2﹣1),
当a<0时,对称轴在y轴左侧,
∵x≥0,
∴最低点就是A(0,﹣1),
如图所示:
∵图象的最低点到直线y=2a的距离为2,
∴|2a﹣(﹣1)|=3,
解得:a=﹣2或a=1(舍去),
当a>0,对称轴在y轴右侧,
∵x≥0,
∴顶点(a,﹣a2﹣1)就是最低点,
如图所示:
∴2a﹣(﹣a2﹣1)=3,
整理得:(a+1)2=3,
解得:a1=﹣1﹣(不合题意舍去),a2=﹣1+;
综上所述,a的值为﹣2或﹣1+;
18.解:(1)当y1=0时,即﹣x2+4=0,解得x=2或x=﹣2,
又点A在x轴的负半轴,
∴点A(﹣2,0),
∵点A(﹣2,0),是抛物线y2的最高点.
∴﹣=﹣2,即b=﹣,
把A(﹣2,0)代入y2=﹣x2﹣x+c得,c=﹣,
∴抛物线y2的解析式为:y2=﹣x2﹣x﹣;
由得,,,
∵A(﹣2,0),
∴点B(3,﹣5),
答:抛物线y2的解析式为:y2=﹣x2﹣x﹣,点B(3,﹣5);
(2)由题意得,CD=y1﹣y2=﹣x2+4﹣(﹣x2﹣x﹣),
即:CD=﹣x2+x+,
当x=﹣=时,CD最大=﹣×+×+=5,
∴S△BCD=×5×(3﹣)=.
19.解:(1)如图所示,点B的坐标为(3,0),点C的坐标为(0,3),
(2)设抛物线解析式为y=a(x﹣1)(x﹣3)(a≠0),
把(0,3)代入得:3a=3,
解得:a=1,
∴抛物线解析式为y=x2﹣4x+3.
1.函数写成y=a(x﹣h)2+k的形式是( )
A. B.
C. D.
2.已知抛物线与二次函数y=2x2的图象的开口大小相同,开口方向相反,且顶点坐标为(﹣1,2021),则该抛物线对应的函数表达式为( )
A.y=﹣2(x﹣1)2+2021 B.y=2(x﹣1)2+2021
C.y=2(x+1)2+2021 D.y=﹣2(x+1)2+2021
3.如图是一个不倒翁的部分剖面图,可看作一个抛物线,若肚子最大的宽度AB=10cm,OD=15cm,按图示位置建立的平面直角坐标系可知,抛物线表达式为( )
A.y=x2 B.y=﹣x2 C.y=x2 D.y=﹣x2
4.已知二次函数的图象如图所示,那么此函数的解析式只可能是( )
A.y=﹣x2+x+3 B.y=﹣x2﹣3x﹣3 C.y=﹣x2﹣x+3 D.y=x2+x+3
5.顶点为(﹣6,0),开口向下,形状与函数y=x2的图象相同的抛物线的表达式是 .
6.已知抛物线与x轴交点的横坐标分别为3,1;与y轴交点的纵坐标为6,则二次函数的关系式是 .
7.在平面直角坐标系中,抛物线y=ax2+bx+c的顶点为A,且经过平行四边形ABCD的顶点A,B(1,m),D(7,1),它的对称轴经过AC,BD的交点,若AB=5,则这条抛物线的解析式为 .
8.已知某抛物线的顶点为(2,4),且过点(1,2).
(1)求抛物线的解析式;
(2)动点P(a,6)能否在抛物线上?请说明理由;
(3)若点A(m,y1),B(n,y2)都在抛物线上,且m<n<0,比较y1,y2的大小,并说明理由.
9.如图所示,抛物线y=ax2+bx+4(a≠0)经过点A(﹣1,0),点B(4,0),与y轴交于点C,连接AC,BC.点M是线段OB上不与点O、B重合的点,过点M作DM⊥x轴,交抛物线于点D,交BC于点E.
(1)求抛物线的表达式;
(2)过点D作DF⊥BC,垂足为点F.设M点的坐标为M(m,0),请用含m的代数式表示线段DF的长,并求出当m为何值时DF有最大值,最大值是多少?
10.如图,抛物线y=ax2﹣6ax+3交y轴于点A,AB∥x轴交抛物线于另一点B,抛物线的顶点为C,AC=AB.
(1)求抛物线的函数表达式.
(2)P(0,b)是y轴上一点,过点P作y轴的垂线交抛物线的对称轴于点D,取PD的中点M,若点M恰好落在抛物线上,求b的值.
11.如图,在平面直角坐标系中,点A的坐标为(﹣1,0),点B,点C分别为x轴,y轴正半轴上一点,其满足OC=OB=2OA.
(1)求过A,B,C三点的抛物线的表达式;
(2)连接CA,CB,若点P是x轴下方抛物线上的一点,连接PC,PB,当S△PCB=S△ACB时,求点P的坐标.
12.已知抛物线y=ax2+2ax+5﹣a2经过点(﹣3,﹣5).
(1)求该抛物线的表达式及顶点坐标.
(2)设点A(m,y1),B(1,y2)在抛物线上,若y1>y2,求m的取值范围.
13.如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0)
(1)求抛物线的解析式和顶点E坐标;
(2)该抛物线有一点D,使得S△DBC=S△EBC,求点D的坐标.
14.如图,抛物线的顶点为A(﹣3,﹣3),此抛物线交x轴于O、B两点.
(1)求此抛物线的解析式;
(2)求△AOB的面积;
(3)若抛物线上另一点P满足S△POB=S△AOB,请求出点P的坐标.
15.如图,已知抛物线的顶点为A(0,1),矩形CDEF的顶点C、F在抛物线上,点D、E在x轴上,CF交y轴于点B(0,2),且矩形面积为8.
(1)求此抛物线的解析式;
(2)求当﹣1≤x≤3时,y的取值范围;
(3)直接写出当y>3时,x的取值范围.
16.如图,在平面直角坐标系中,∠AOB=90°,AO=BO,点A的坐标为(﹣1,3).
(1)求点B的坐标;
(2)抛物线y=ax2+bx经过点A、B,求它的解析式.
17.平面直角坐标系中,函数y=x2﹣2ax﹣1(a为常数)的图象与y轴交于点A.
(1)直接写出A点坐标;
(2)当此函数图象经过点(1,2)时,求此函数表达式,并写出函数y随x增大而增大时x的取值范围;
(3)当x≥0时,若函数y=x2﹣2ax﹣1(a为常数)图象最低点到直线y=2a的距离为3,求a的值.
18.如图,两条抛物线y1=﹣x2+4,y2=﹣x2+bx+c相交于A,B两点,点A在x轴负半轴上,且为抛物线y2的最高点.
(1)求抛物线y2的解析式和点B的坐标;
(2)点C是抛物线y1上A,B之间的一点,过点C作x轴的垂线交y2于点D,当线段CD取最大值时,求S△BCD.
19.如图,在平面坐标系xOy中,点A的坐标为(1,0),点P的横坐标为2,将点A绕点P旋转,使它的对应点B恰好落在x轴上(不与A点重合);再将点B绕点O逆时针旋转90°得到点C.
(1)直接写出点B和点C的坐标;
(2)求经过A,B,C三点的抛物线的表达式.
参考答案
1.解:=﹣(x2﹣6x+9﹣9)﹣2=(x﹣3)2+1,即y=(x﹣1)2+.
故选:D.
2.解:∵抛物线的顶点坐标为(﹣1,2021),
∴抛物线的解析式为y=a(x+1)2+2021,
∵抛物线y=a(x+1)2+2021二次函数y=2x2的图象的开口大小相同,开口方向相反,
∴a=﹣2,
∴抛物线的解析式为y=﹣2(x+1)2+2021.
故选:D.
3.解:由题意可知A(﹣5,15),B(5,15),顶点是原点,
设抛物线的解析式为y=ax2,
∴15=25a,
解得a=,
∴抛物线表达式为y=x2,
故选:A.
4.解:∵抛物线开口向下,
∴a<0,
∵对称轴在y轴的左侧,
∴a、b同号,
∴b<0,
∵抛物线交y轴的正半轴,
∴c>0.
故选:C.
5.解:设所求的抛物线的关系式为y=a(x﹣h)2+k,
∵顶点为(﹣6,0),
∴h=﹣6,k=0,
又∵开口向下,形状与函数y=x2的图象相同,
∴a=﹣,
∴抛物线的关系式为:y=﹣(x+6)2,
6.解:设所求抛物线是y=ax2+bx+c,根据题意得,
,
解得
,
故所求函数解析式是y=2x2﹣8x+6.
故答案是y=2x2﹣8x+6.
7.解:设抛物线的解析式为y=ax2+bx+c(a≠0),
因为四边形ABCD是平行四边形,
所以AC,BD互相平分且O'为AC,BD的中点,
又因为B(1,m),D(7,1),
所以,
所以抛物线对称轴为直线x=4,
过点A作AE⊥直线x=1于点E,
因为AE=3,AB=5,由勾股定理可得“,
又因为B(1,m),所以A(4,m﹣4)或(4,m+4),
因为B在抛物线上,所以B(1,a+b+c),A(4,a+b+c﹣4)或(4,a+b+c+4),
根据抛物线经过点D(7,1),A(4,a+b+c﹣4)或(4,a+b+c+4)且对称轴为直线x=4可列方程为:
或,
解得:或.
故抛物线的解析式为:或y=﹣+﹣.
8.解:(1)设抛物线的解析式为y=a(x﹣2)2+4,
将(1,2)代入上式得2=a(1﹣2)2+4,
解得a=﹣2,
∴抛物线的解析式为y=﹣2(x﹣2)2+4,
(2)动点P(a,6)不在抛物线上,理由如下:
∵抛物线y=﹣2(x﹣2)2+4的最大值为4,
∴动点P(a,6)不在抛物线上;
(3)∵抛物线的函数关系式为:y=﹣2(x﹣2)2+4,
∴抛物线的开口向下,对称轴为直线x=2,
∴当x<2时,y随x的增大而增大,
∵点A(m,y1),B(n,y2)都在抛物线上,且m<n<0<2,
∴y1<y2.
9.解:(1)A(﹣1,0),B(4,0)分别代入y=ax2+bx+4(a≠0)得,
解得:,
∴抛物线的表达式为:y=﹣x2+3x+4;
(2)把x=0代入y=﹣x2+3x+4得y=4,
∴C(0,4),
设BC所在直线解析式为y=kx+b,
把B(4,0),C(0,4)代入y=kx+b得:
,
解得,
∴y=﹣x+4,
设M(m,0),则D(m,﹣m2+3m+4),E(m,﹣m+4),
∴DE=﹣m2+3m+4+m﹣4=﹣m2+4m,
∵OB=OC=4,OC⊥OB,
∴∠OBC=∠OCB=45°,
∵DM⊥x轴,
∴∠DEF=∠BEM=45°,
又∵DF⊥BC,
∴DF=DE=(﹣m2+4m)=(m﹣2)2+2,
∵<0,
∴当m=2时,DF有最大值为2.
10.解:(1)抛物线y=ax2﹣6ax+3交y轴于点A,
令x=0,则y=3,
∴点A(0,3),
对称轴为:x=﹣=3,
∵AB∥x轴,
∴A、B关于x=3对称,
∴B(6,3),则AB=6,
又AC=AB=5,
过C作AB的垂线CN,
则AN=3,
在Rt△ACN中,
由勾股定理得:CN===4,
∴C(3,﹣1),
把C点坐标代入y=ax2﹣6ax+3得,
﹣1=9a﹣18a+3,
解得:a=,
∴抛物线函数表达式为:y=x2﹣x+3.
(2)由题意得:D点坐标为(3,b),
∵M为PD中点,
∴M(,b),
又∵M在抛物线上,代入得:
b=×﹣×+3=0,
∴b=0.
11.解:(1)∵点A的坐标为(﹣1,0),OC=OB=2OA.
∴B(2,0),C(0,2),
设过A、B、C三点的抛物线的解析式为y=a(x﹣2)(x+1),
把点C(0,2)代入,解得:a=﹣1,
所以抛物线的解析式为:y=﹣(x﹣2)(x+1)=﹣x2+x+2;
(2)如图,
∵S△ACB=AB OC=×3×2=3,
∴S△PCB=S△ACB=4,
∵点P是x轴下方抛物线上的一点,设P(m,﹣m2+m+2),
∴直线PC为y=(﹣m+1)x+2,y=0时,x=,m<﹣1或m>2,
∴S△PCB=BM [2﹣(﹣m2+m+2)]=×(2﹣)×(m2﹣m)=4,
解得:m=1﹣,
∴点P的坐标为(1+,﹣3﹣)或(1﹣,﹣3).
12.解:(1)∵抛物线y=ax2+2ax+5﹣a2经过点(﹣3,﹣5),
∴﹣5=9a﹣6a+5﹣a2,
解得a1=﹣2,a2=5,
当a=﹣2时,该抛物线的表达式是y=﹣2x2﹣4x+1=﹣2(x+1)2+3,顶点坐标为(﹣1,3),
当a=5时,该抛物线的表达式是y=5x2+10x﹣20=5(x+1)2﹣25,顶点坐标为(﹣1,﹣25),
由上可得,当a=﹣2时,该抛物线的表达式是y=﹣2x2﹣4x+1,顶点坐标为(﹣1,3);
当a=5时,该抛物线的表达式是y=5x2+10x﹣20,顶点坐标为(﹣1,﹣25);
(2)∵点A(m,y1),B(1,y2)在抛物线上,y1>y2,
∴当a=﹣2时,抛物线的表达式是y=﹣2x2﹣4x+1,顶点坐标为(﹣1,3),则﹣3<m<1;
当a=5时,该抛物线的表达式是y=5x2+10x﹣20,顶点坐标为(﹣1,﹣25),则m>1或m<﹣3.
13.解:(1)由题意,设y=a(x﹣1)(x﹣5),
代入A(0,4),得,
∴,
∴,
故顶点E坐标为;
(2)∵S△DBC=S△EBC,
∴两个三角形在公共边BC上的高相等,
又点E到BC的距离为,
∴点D到BC的距离也为,
则(x﹣3)2﹣=,
解得x=3±2,
则点D或.
14.解:(1)如图,连接AB、OA.设抛物线的解析式为y=a(x+3)2﹣3,
把(0,0)代入得a×32﹣3=0,解得a=,
所以此抛物线的解析式为y=(x+3)2﹣3;
(2)∵抛物线的对称轴为直线x=﹣3,
∴B点坐标为(﹣6,0),
∴△AOB的面积=×6×3=9;
(3)设P点坐标为(x,y),
∵S△POB=S△AOB,
∴|y|×6=9,
解得y=3或y=﹣3(舍去),
∴(x+3)2﹣3=3,
解得x1=3﹣3,x2=﹣3﹣3,
∴P点坐标为(3﹣3,3),(﹣3﹣3,3).
15.解:(1)∵A(0,1)为抛物线顶点,
∴抛物线对称轴为y轴,
∵C,F在抛物线上,
∴BC=BF,
∵矩形CDEF面积为CF OB=8,
∴CF==4,
∴BC=BF=2,
∴点F坐标为(2,2),
设抛物线解析式为y=ax2+1,
把(2,2)代入解析式得2=4a+1,
解得a=,
∴抛物线解析式为y=x2+1.
(2)∵抛物线开口向上,对称轴为y轴,
∴当x=0时,y取最小值为1,
∵3﹣0>0﹣(﹣1),
∴x=3时y取最大值,
把x=3代入y=x2+1得.
∴1≤y≤.
(3)把y=3代入y=x2+1得3=x2+1,
解得x=﹣2或x=2,
∴y>3时,x<﹣2或x>2.
16.解:(1)作AC⊥x轴于点C,BD⊥x轴于点D.
∴∠ACO=∠BDO=90°,∠AOC+∠CAO=90°.
∵∠AOB=90°,
∴∠AOC+∠BOD=90°.
∴∠CAO=∠BOD.
又∵AO=BO,
∴△AOC≌△OBD(AAS).
又∵A(﹣1,3),
∴AC=OD=3,OC=BD=1,
∴B(3,1).
(2)由抛物线y=ax2+bx经过点A(﹣1,3)、B(3,1)得,
解得,
∴解析式为.
17.解:(1)当x=0时,y=x2﹣2ax﹣1=﹣1,
∴点A的坐标为:(0,﹣1);
(2)将点(1,2)代入y=x2﹣2ax﹣1,
得:2=1﹣2a﹣1,
解得:a=﹣1,
∴函数的表达式为:y=x2+2x﹣1,
∵y=x2+2x﹣1=(x+1)2﹣2,
∴抛物线的开口向上,对称轴为直线x=﹣1,
∴当x≥﹣1时,y随x的增大而增大;
(3)抛物线y=x2﹣2ax﹣1=(x﹣a)2﹣a2﹣1的对称轴为:x=a,顶点坐标为:(a,﹣a2﹣1),
当a<0时,对称轴在y轴左侧,
∵x≥0,
∴最低点就是A(0,﹣1),
如图所示:
∵图象的最低点到直线y=2a的距离为2,
∴|2a﹣(﹣1)|=3,
解得:a=﹣2或a=1(舍去),
当a>0,对称轴在y轴右侧,
∵x≥0,
∴顶点(a,﹣a2﹣1)就是最低点,
如图所示:
∴2a﹣(﹣a2﹣1)=3,
整理得:(a+1)2=3,
解得:a1=﹣1﹣(不合题意舍去),a2=﹣1+;
综上所述,a的值为﹣2或﹣1+;
18.解:(1)当y1=0时,即﹣x2+4=0,解得x=2或x=﹣2,
又点A在x轴的负半轴,
∴点A(﹣2,0),
∵点A(﹣2,0),是抛物线y2的最高点.
∴﹣=﹣2,即b=﹣,
把A(﹣2,0)代入y2=﹣x2﹣x+c得,c=﹣,
∴抛物线y2的解析式为:y2=﹣x2﹣x﹣;
由得,,,
∵A(﹣2,0),
∴点B(3,﹣5),
答:抛物线y2的解析式为:y2=﹣x2﹣x﹣,点B(3,﹣5);
(2)由题意得,CD=y1﹣y2=﹣x2+4﹣(﹣x2﹣x﹣),
即:CD=﹣x2+x+,
当x=﹣=时,CD最大=﹣×+×+=5,
∴S△BCD=×5×(3﹣)=.
19.解:(1)如图所示,点B的坐标为(3,0),点C的坐标为(0,3),
(2)设抛物线解析式为y=a(x﹣1)(x﹣3)(a≠0),
把(0,3)代入得:3a=3,
解得:a=1,
∴抛物线解析式为y=x2﹣4x+3.
