2021-2022学年北师大版九年级数学下册2.2二次函数的图象与性质培优训练(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册2.2二次函数的图象与性质培优训练(Word版,附答案解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 542.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览


文档简介
2021-2022学年北师大版九年级数学下册《2.2二次函数的图象与性质》培优训练(附答案)
一.选择题(共8小题)
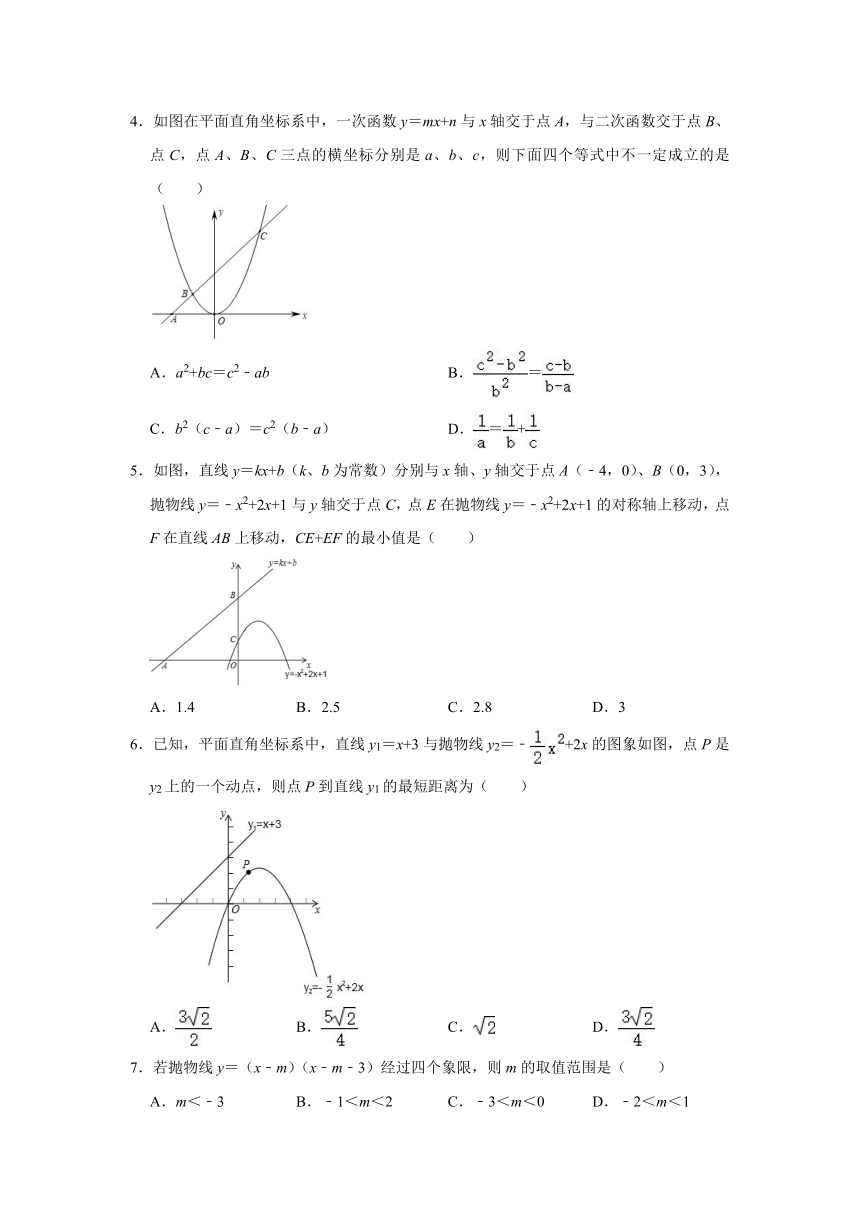
1.如图,抛物线y=ax2+bx+c的对称轴为x=﹣1,且过点(,0),有下列结论:
①abc>0; ②a﹣2b+4c>0;③25a﹣10b+4c=0;④3b+2c>0;
其中所有正确的结论是( )
A.①③ B.①③④ C.①②③ D.①②③④
2.如图,函数y=ax2+bx+c的图象过点(﹣1,0)和(m,0),请思考下列判断:
①abc<0;②4a+c<2b;③=1﹣;④am2+(2a+b)m+a+b+c<0;⑤|am+a|=正确的是( )
A.①③⑤ B.①②③④⑤ C.①③④ D.①②③⑤
3.已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )
A.abc>0 B.b2﹣4ac<0 C.9a+3b+c>0 D.c+8a<0
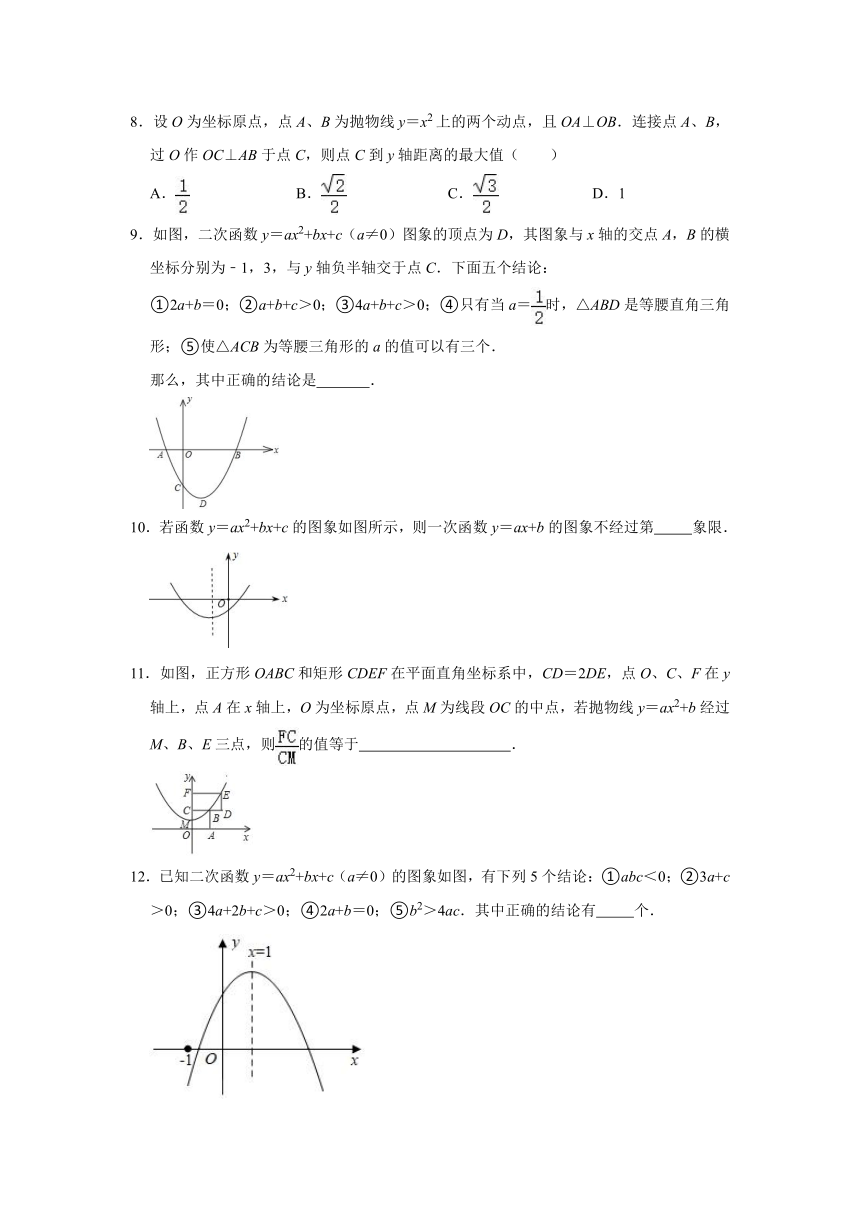
4.如图在平面直角坐标系中,一次函数y=mx+n与x轴交于点A,与二次函数交于点B、点C,点A、B、C三点的横坐标分别是a、b、c,则下面四个等式中不一定成立的是( )
A.a2+bc=c2﹣ab B.=
C.b2(c﹣a)=c2(b﹣a) D.=+
5.如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(﹣4,0)、B(0,3),抛物线y=﹣x2+2x+1与y轴交于点C,点E在抛物线y=﹣x2+2x+1的对称轴上移动,点F在直线AB上移动,CE+EF的最小值是( )
A.1.4 B.2.5 C.2.8 D.3
6.已知,平面直角坐标系中,直线y1=x+3与抛物线y2=﹣+2x的图象如图,点P是y2上的一个动点,则点P到直线y1的最短距离为( )
A. B. C. D.
7.若抛物线y=(x﹣m)(x﹣m﹣3)经过四个象限,则m的取值范围是( )
A.m<﹣3 B.﹣1<m<2 C.﹣3<m<0 D.﹣2<m<1
8.设O为坐标原点,点A、B为抛物线y=x2上的两个动点,且OA⊥OB.连接点A、B,过O作OC⊥AB于点C,则点C到y轴距离的最大值( )
A. B. C. D.1
9.如图,二次函数y=ax2+bx+c(a≠0)图象的顶点为D,其图象与x轴的交点A,B的横坐标分别为﹣1,3,与y轴负半轴交于点C.下面五个结论:
①2a+b=0;②a+b+c>0;③4a+b+c>0;④只有当a=时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值可以有三个.
那么,其中正确的结论是 .
10.若函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b的图象不经过第 象限.
11.如图,正方形OABC和矩形CDEF在平面直角坐标系中,CD=2DE,点O、C、F在y轴上,点A在x轴上,O为坐标原点,点M为线段OC的中点,若抛物线y=ax2+b经过M、B、E三点,则的值等于 .
12.已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:①abc<0;②3a+c>0;③4a+2b+c>0;④2a+b=0;⑤b2>4ac.其中正确的结论有 个.
13.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:
x … ﹣1 0 1 4 …
y … 10 5 2 5 …
则当x≥1时,y的最小值是 .
14.已知M、N两点关于y轴对称,且点M在双曲线上,点N在直线y=﹣x+3上,设点M坐标为(a,b),则y=﹣abx2+(a+b)x的顶点坐标为 .
15.如图,正方形ABCD的边长为2,E为边AD上一动点,连接BE、CE,以CE为边向右侧作正方形CEFG.
(1)若BE=,则正方形CEFG的面积为 ;
(2)连接DF、DG,则△DFG面积的最小值为 .
16.已知矩形长与宽分别为a、b(a>b),截一个面积最大的菱形,使菱形的顶点落在矩形的边上,该菱形最大面积为 .
17.当﹣1≤x≤1时,函数y=﹣x2﹣2mx+2n+1的最小值是﹣4,最大值是0,则m、n的值分别是 .
18.在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(﹣2,6),C(2,2)两点.
(1)记抛物线顶点为D,求△BCD的面积;
(2)若直线y=﹣x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.
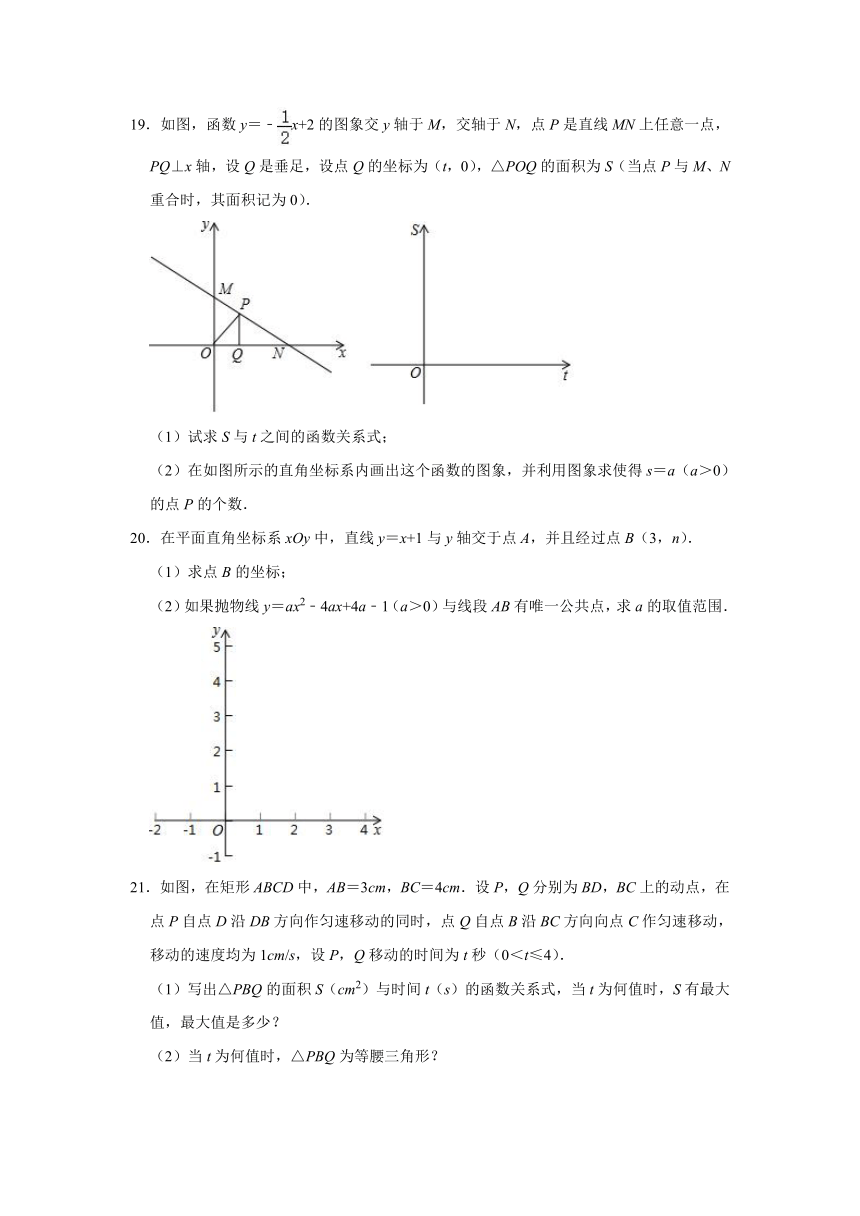
19.如图,函数y=﹣x+2的图象交y轴于M,交轴于N,点P是直线MN上任意一点,PQ⊥x轴,设Q是垂足,设点Q的坐标为(t,0),△POQ的面积为S(当点P与M、N重合时,其面积记为0).
(1)试求S与t之间的函数关系式;
(2)在如图所示的直角坐标系内画出这个函数的图象,并利用图象求使得s=a(a>0)的点P的个数.
20.在平面直角坐标系xOy中,直线y=x+1与y轴交于点A,并且经过点B(3,n).
(1)求点B的坐标;
(2)如果抛物线y=ax2﹣4ax+4a﹣1(a>0)与线段AB有唯一公共点,求a的取值范围.
21.如图,在矩形ABCD中,AB=3cm,BC=4cm.设P,Q分别为BD,BC上的动点,在点P自点D沿DB方向作匀速移动的同时,点Q自点B沿BC方向向点C作匀速移动,移动的速度均为1cm/s,设P,Q移动的时间为t秒(0<t≤4).
(1)写出△PBQ的面积S(cm2)与时间t(s)的函数关系式,当t为何值时,S有最大值,最大值是多少?
(2)当t为何值时,△PBQ为等腰三角形?
22.如图,已知抛物线y=x2+bx+c经过A(﹣1,0),B(3,0)两点.
(1)求b和c;
(2)当0<x<4时,求y的取值范围;
(3)点P为x轴下方抛物线上一点,试说明P点运动到哪个位置时S△PAB最大,并求出最大面积.
23.如图,在平面直角坐标系中,抛物线y=﹣x2﹣x+与直线y=x+b交于A、B两点,其中点A在x轴上,点P是直线AB上方的抛物线上一动点(不与点A、B重合)过P作y轴的平行线交直线于点C,连接PA、PB.
(1)求直线的解析式及A、B点的坐标;
(2)当△APB面积最大时,求点P的坐标以及最大面积.
参考答案
1.解:①观察图象可知:
a<0,b<0,c>0,∴abc>0,
所以①正确;
②当x=时,y=0,
即a+b+c=0,
∴a+2b+4c=0,
∴a+4c=﹣2b,
∴a﹣2b+4c=﹣4b>0,
所以②正确;
③因为对称轴x=﹣1,抛物线与x轴的交点(,0),
所以与x轴的另一个交点为(﹣,0),
当x=﹣时,a﹣b+c=0,
∴25a﹣10b+4c=0.
所以③正确;
④当x=时,a+2b+4c=0,
又对称轴:﹣=﹣1,
∴b=2a,a=b,
b+2b+4c=0,
∴b=﹣c.
∴3b+2c=﹣c+2c=﹣c<0,
∴3b+2c<0.
所以④错误.
或者∵当x=1时,a+b+c<0,
∴c<﹣a﹣b,
又∵b=2a,
∴a=b,
∴c<﹣b,
∴2c<﹣3b,
∴2c+3b<0,
∴结论④错误
故选:C.
2.解:∵抛物线开口向下,
∴a<0,
∵抛物线交y轴于正半轴,
∴c>0,
∵﹣>0,
∴b>0,
∴abc<0,故①正确,
∵x=﹣2时,y<0,
∴4a﹣2b+c<0,即4a+c<2b,故②正确,
∵y=ax2+bx+c的图象过点(﹣1,0)和(m,0),
∴﹣1×m=,am2+bm+c=0,
∴++=0,
∴=1﹣,故③正确,
∵﹣1+m=﹣,
∴﹣a+am=﹣b,
∴am=a﹣b,
∵am2+(2a+b)m+a+b+c
=am2+bm+c+2am+a+b
=2a﹣2b+a+b
=3a﹣b<0,故④正确,
∵m+1=|﹣|,
∴m+1=||,
∴|am+a|=,故⑤正确,
故选:B.
3.解:A.∵二次函数的图象开口向下,图象与y轴交于y轴的正半轴上,
∴a<0,c>0,
∵抛物线的对称轴是直线x=1,
∴﹣=1,
∴b=﹣2a>0,
∴abc<0,故本选项错误;
B.∵图象与x轴有两个交点,
∴b2﹣4ac>0,故本选项错误;
C.∵对称轴是直线x=1,与x轴一个交点是(﹣1,0),
∴与x轴另一个交点的坐标是(3,0),
把x=3代入二次函数y=ax2+bx+c(a≠0)得:y=9a+3b+c=0,故本选项错误;
D.∵当x=3时,y=0,
∵b=﹣2a,
∴y=ax2﹣2ax+c,
把x=4代入得:y=16a﹣8a+c=8a+c<0,
故选:D.
4.解:一次函数y=mx+n与x轴的轴交于点A,故点(a,0),
将点A(a,0)坐标代入一次函数表达式得:0=am+n,
解得:n=﹣am,
故一次函数的表达式为y=mx﹣am,
∵点B、C在一次函数上,故点B、C的坐标分别为(b,mb﹣ma)、(c,mc﹣ma),
设二次函数的表达式为y=Ax2,
点B、C在该二次函数上,则,
(1)②﹣①得:A(b2﹣c2)=m(c﹣b),等式两边同除以Ab2得,,即,故B正确,不符合题意;
(2)①÷②得:③,即C正确,不符合题意;
(3)化简③得:a=,即=,故D正确,不符合题意;
(4)化简A得:a2﹣c2=﹣bc﹣ab,化简得:a+b=c,而从上述各式看,该式不一定成立,故A符合题意,
故选:A.
5.解:如图,设C点关于抛物线对称轴的对称点为C′,由对称的性质可得CE=C′E,
∴CE+EF=C′E+EF,
∴当F、E、C′三点一线且C′F与AB垂直时CE+EF最小,
由题意可得,解得,
∴直线解析式为y=x+3;
∵C(0,1),
∴C′(2,1),
∴直线C′F的解析式为y=﹣x+,
由,解得,
∴F(,),
∴C′F==
即CE+EF的最小值为.
故选:C.
6.解:设过点P平行直线y1的解析式为y=x+b,
当直线y=x+b与抛物线只有一个交点时,点P到直线y1的距离最小,
由,消去y得到:x2﹣2x+2b=0,
当Δ=0时,4﹣8b=0,
∴b=,
∴直线的解析式为y=x+,
如图设直线y1交x轴于A,交y轴于B,直线y=x+交x轴于C,作CD⊥AB于D,PE⊥AB于E,则A(﹣3,0),B(0,3),C(﹣,0)
∴OA=OB=3,OC=,AC=,
∴∠DAC=45°,
∴CD==,
∵AB∥PC,CD⊥AB,PE⊥AB,
∴PE=CD=,
故选:B.
7.解:令y=0,得 (x﹣m)(x﹣m﹣3)=0,
解得x1=m,x2=m+3,
∴抛物线与x轴的两个交点为(m,0 )和(m+3,0),
∵抛物线经过四个象限,
∴(m,0 )和(m+3,0)分别位于原点两侧,
即 m<0<m+3,
∴﹣3<m<0,
故选:C.
8.解:如图,分别作AE、BF垂直于x轴于点E、F,
设OE=a,OF=b,由抛物线解析式为y=x2,
则AE=a2,BF=b2,
作AH⊥BF于H,交y轴于点G,连接AB交y轴于点D,
设点D(0,m),
∵DG∥BH,
∴△ADG∽△ABH,
∴,即.
化简得:m=ab.
∵∠AOB=90°,
∴∠AOE+∠BOF=90°,
又∠AOE+∠EAO=90°,
∴∠BOF=∠EAO,
又∠AEO=∠BFO=90°,
∴△AEO∽△OFB.
∴,
即,
化简得ab=1.
则m=ab=1,说明直线AB过定点D,D点坐标为(0,1).
∵∠DCO=90°,DO=1,
∴点C是在以DO为直径的圆上运动,
∴当点C到y轴距离为=时,点C到y轴距离的最大.
故选:A.
9.解:①∵图象与x轴的交点A,B的横坐标分别为﹣1,3,
∴AB=4,
∴对称轴x==1,
即2a+b=0;
故①正确;
②由抛物线的开口方向向上可推出a>0,而>0
∴b<0,
∵对称轴x=1,
∴当x=1时,y<0,
∴a+b+c<0;
故②错误;
③∵图象与x轴的交点A,B的横坐标分别为﹣1,3,
∴a﹣b+c=0,9a+3b+c=0,
∴10a+2b+2c=0,
∴5a+b+c=0,
∴a+4a+b+c=0,
∵a>0,
∴4a+b+c<0,
故③错误;
④要使△ABD为等腰直角三角形,必须保证D到x轴的距离等于AB长的一半;
D到x轴的距离就是当x=1时y的值的绝对值.
当x=1时,y=a+b+c,
即|a+b+c|=2,
∵当x=1时y<0,
∴a+b+c=﹣2,
又∵图象与x轴的交点A,B的横坐标分别为﹣1,3,
∴当x=﹣1时y=0即a﹣b+c=0;
x=3时y=0.
∴9a+3b+c=0,
解这三个方程可得:b=﹣1,a=,c=﹣;
⑤要使△ACB为等腰三角形,则必须保证AB=BC=4或AB=AC=4或AC=BC,
当AB=BC=4时,
∵AO=1,△BOC为直角三角形,
又∵OC的长即为|c|,
∴c2=16﹣9=7,
∵由抛物线与y轴的交点在y轴的负半轴上,
∴c=﹣,
与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=;
同理当AB=AC=4时,
∵AO=1,△AOC为直角三角形,
又∵OC的长即为|c|,
∴c2=16﹣1=15,
∵由抛物线与y轴的交点在y轴的负半轴上,
∴c=﹣
与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=;
同理当AC=BC时
在△AOC中,AC2=1+c2,
在△BOC中BC2=c2+9,
∵AC=BC,
∴1+c2=c2+9,此方程无解.
经解方程组可知只有两个a值满足条件.
故⑤错误.
故答案为:①④.
10.解:∵抛物线的开口向上,
∴a>0;
∵对称轴为x=<0,
∴a、b同号,即b>0.
∴一次函数y=ax+b的图象不经过第四象限.
11.解:设正方形OABC的边长为m,DE=n,CD=EF=2n,
∵点M为OC的中点,
∴点M为(0,m)、点B为(m,m)和点E为(2n,m+n),
∵抛物线y=ax2+b经过M,B,E三点,
∴m=am2+,
解得:a=,
∴抛物线y=x2+,
把点E(2n,m+n)代入抛物线得
m+n= 4n2+,
解得:m=(﹣1)n或m=(﹣﹣1)n不合题意,舍去),
∴==.
12.解:抛物线开口向下,因此a<0,对称轴为x=1>0,因此a、b异号,所以b>0,抛物线与y轴交点在正半轴,因此c>0,所以abc<0,于是①正确;
抛物线的对称轴为直线x=﹣=1,因此有2a+b=0,故④正确;
当x=﹣1时,y=a﹣b+c<0,而2a+b=0,所以3a+c<0,故②不正确;
抛物线与x轴有两个不同交点,因此b2﹣4ac>0,即b2>4ac,故⑤正确;
抛物线的对称轴为x=1,与x轴的一个交点在﹣1与0之间,因此另一个交点在2与3之间,于是当x=2时,y=4a+2b+c>0,因此③正确;
综上所述,正确的结论有:①③④⑤,
故答案为:4.
13.解:∵由表可知,当x=﹣1时,y=10,当x=0时,y=5,当x=1时,y=2,
∴,解得,
∴抛物线的解析式为y=x2﹣4x+5,
∴其对称轴为直线x=﹣=﹣=2.
∵x≥1,
∴当x=2时,y最小===1.
故答案为:1.
14.解:∵M、N两点关于y轴对称,
∴M坐标为(a,b),N为(﹣a,b),分别代入相应的函数中得,b=①,a+3=b②,∴ab=,(a+b)2=(a﹣b)2+4ab=11,a+b=±,
∴y=﹣x2±x,
∵=±,=,
∴顶点坐标(,)或(﹣,).
故答案为:(,)或(﹣,).
15.解:(1)∵四边形ABCD是正方形,
∴AB=AD=2,∠A=∠D=90°,
∵BE=,
∴AE===1,
∴DE=AD﹣AE=2﹣1=1,
∴EC2=DE2+CD2=12+22=5,
∴正方形CEFG的面积=EC2=5.
故答案为5;
(2)连接DF,DG.设DE=x,则CE=,
∵S△DEC+S△DFG=S正方形ECGF,
∴S△DFG=(x2+4)﹣×x×2
=x2﹣x+2
=(x﹣1)2+,
∵>0,
∴x=1时,△DFG的面积的最小值为.
故答案为.
16.解:∵菱形顶点都落在矩形边上,
∴菱形的高为b,
当底最长时菱形面积最大,
此时菱形两个顶点与矩形顶点重合,如图,
设BF=DF=x,则CF=a﹣x,
在Rt△CDF中,由勾股定理得:
FC2+CD2=DF2,
即(a﹣x)2+b2=x2,
解得x=,
∴S菱形BFDE=BF CD=.
故答案为:.
17.解:∵函数y=﹣x2﹣2mx+2n+1=﹣(x+m)2+m2+2n+1,
∴该函数图象开口向下,对称轴为直线x=﹣m,
∵当﹣1≤x≤1时,函数y=﹣x2﹣2mx+2n+1的最小值是﹣4,最大值是0,
∴当﹣m<﹣1时,m>1,当x=﹣1时,y=0,当x=1时,y=﹣4,
即,解得,不符合m>1,故此种情况不存在;
当﹣1≤﹣m≤1时,﹣1≤m≤1,x=﹣m时,y=0,当x=﹣1时y=﹣4或x=1时y=﹣4,
即或,
解得或;
当﹣m>1时,m<﹣1,当x=1时,y=0,x=﹣1时,y=﹣4,
即,
解得,不符合m<﹣1,故此种情况不存在;
由上可得,m、n的值分别是﹣1,﹣1或1,﹣1,
故答案为:﹣1,﹣1或1,﹣1.
18.解:(1)把B(﹣2,6),C(2,2)两点坐标代入得:,
解这个方程组,得 ,
∴抛物线的解析式为y=x2﹣x+2;
∵y=x2﹣x+2=(x﹣1)2+,
∴顶点D(1,),
∵B(﹣2,6),C(2,2),
∵直线BC为y=﹣x+4,
∴对称轴与BC的交点H(1,3),
∴S△BDC=S△BDH+S△DHC=×(3﹣) 3+×(3﹣) 1=3.
(2)由消去y得到x2﹣x+4﹣2b=0,
当Δ=0时,直线与抛物线相切,1﹣4(4﹣2b)=0,
∴b=,
当直线y=﹣x+b经过点C时,b=3,
当直线y=﹣x+b经过点B时,b=5,
∵直线y=﹣x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,
∴<b≤3.
19.解:(1)①当t<0时,OQ=﹣t,PQ=﹣t+2,
∴S= (﹣t)(﹣t+2)=t2﹣t;
②当0<t<4时,OQ=t,PQ=﹣t+2,
∴S= t(﹣t+2)=﹣t2+t;
③当t>4时,OQ=t,PQ=﹣(﹣t+2)=t﹣2,
∴S= t(t﹣2)=t2﹣t;
④当t=0或4时,S=0;
于是,S=;
(2)S=
下图中的实线部分就是所画的函数图象.
观察图象可知:
当0<a<1时,符合条件的点P有四个;
当a=1时,符合条件的点P有三个;
当a>1时,符合条件的点P只有两个.
20.解:(1)把x=3代入y=x+1,y=3+1=4,∴点B的坐标为B(3,4);
(2)由题意:线段ABy=x+1(0≤x≤3),
∵y=ax2﹣4ax+4a﹣1=a(x﹣2)2﹣1,
∴抛物线的对称轴为直线x=2,顶点坐标为(2,﹣1),
∵点A(0,1),点B(3,4),
∵当抛物线y=ax2﹣4ax+4a﹣1(a>0)与线段AB有唯一公共点时,
∴①或②
解①得≤a<5,②无解,
综上所述,当≤a<5时,抛物线与线段AB有一个公共点.
21.解:(1)矩形ABCD中,BD===5,
过点P作PM⊥BC,垂足为M,
∴△BPM∽△BDC
∴,
∴PM=(5﹣t),
∴S=t×(5﹣t)=﹣(t﹣)2+,
∴当t=时,S有最大值;
(3)①当BP=BQ时,5﹣t=t,
∴t=,
②当BQ=PQ时,作QE⊥BD,垂足为E,
此时,BE=BP=,
∴△BQE∽△BDC
∴即,
∴t=.
③当BP=PQ时,作PF⊥BC,垂足为F,
此时,BF==t,
∴△BPF∽△BDC
∴即,
∴t=.
∴t=或或均使△PBQ为等腰三角形.
22.解:(1)将点A(﹣1,0),B(3,0)代入抛物线y=x2+bx+c,
得,解得:;
(2)由(1)可知抛物线解析式为y=x2﹣2x﹣3=(x﹣1)2﹣4,即抛物线对称轴为x=1,
所以当x=1时,ymin=﹣4;当x=4时,ymax=5;
而由已知知:0<x<4,所以此时y的范围为﹣4≤y<5;
(3)当点P在抛物线顶点(1,﹣4)时S△PAB最大,
最大面积为S△PAB=AB |yP|=×4×4=8.
23.解:(1)∵y=﹣x2﹣x+,
∴当y=0时,﹣x2﹣x+=0,
解得x1=﹣,x2=1,
∴A点的坐标为(1,0).
将A(1,0)代入y=x+b,
得0=×1+b,
解得b=﹣,
∴直线的解析式为y=x﹣.
由,解得,,
∴B点的坐标为(﹣5,﹣3);
(2)设P(x,﹣x2﹣x+),则C(x,x﹣),
∴PC=(﹣x2﹣x+)﹣(x﹣)=﹣x2﹣4x+5,
∴S△APB=PC |xA﹣xB|
=(﹣x2﹣4x+5)×(1+5)
=﹣3x2﹣12x+15
=﹣3(x+2)2+27,
当x=﹣2时,△APB面积最大,最大值为27,此时点P的坐标为(﹣2,).
一.选择题(共8小题)
1.如图,抛物线y=ax2+bx+c的对称轴为x=﹣1,且过点(,0),有下列结论:
①abc>0; ②a﹣2b+4c>0;③25a﹣10b+4c=0;④3b+2c>0;
其中所有正确的结论是( )
A.①③ B.①③④ C.①②③ D.①②③④
2.如图,函数y=ax2+bx+c的图象过点(﹣1,0)和(m,0),请思考下列判断:
①abc<0;②4a+c<2b;③=1﹣;④am2+(2a+b)m+a+b+c<0;⑤|am+a|=正确的是( )
A.①③⑤ B.①②③④⑤ C.①③④ D.①②③⑤
3.已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )
A.abc>0 B.b2﹣4ac<0 C.9a+3b+c>0 D.c+8a<0
4.如图在平面直角坐标系中,一次函数y=mx+n与x轴交于点A,与二次函数交于点B、点C,点A、B、C三点的横坐标分别是a、b、c,则下面四个等式中不一定成立的是( )
A.a2+bc=c2﹣ab B.=
C.b2(c﹣a)=c2(b﹣a) D.=+
5.如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(﹣4,0)、B(0,3),抛物线y=﹣x2+2x+1与y轴交于点C,点E在抛物线y=﹣x2+2x+1的对称轴上移动,点F在直线AB上移动,CE+EF的最小值是( )
A.1.4 B.2.5 C.2.8 D.3
6.已知,平面直角坐标系中,直线y1=x+3与抛物线y2=﹣+2x的图象如图,点P是y2上的一个动点,则点P到直线y1的最短距离为( )
A. B. C. D.
7.若抛物线y=(x﹣m)(x﹣m﹣3)经过四个象限,则m的取值范围是( )
A.m<﹣3 B.﹣1<m<2 C.﹣3<m<0 D.﹣2<m<1
8.设O为坐标原点,点A、B为抛物线y=x2上的两个动点,且OA⊥OB.连接点A、B,过O作OC⊥AB于点C,则点C到y轴距离的最大值( )
A. B. C. D.1
9.如图,二次函数y=ax2+bx+c(a≠0)图象的顶点为D,其图象与x轴的交点A,B的横坐标分别为﹣1,3,与y轴负半轴交于点C.下面五个结论:
①2a+b=0;②a+b+c>0;③4a+b+c>0;④只有当a=时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值可以有三个.
那么,其中正确的结论是 .
10.若函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b的图象不经过第 象限.
11.如图,正方形OABC和矩形CDEF在平面直角坐标系中,CD=2DE,点O、C、F在y轴上,点A在x轴上,O为坐标原点,点M为线段OC的中点,若抛物线y=ax2+b经过M、B、E三点,则的值等于 .
12.已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:①abc<0;②3a+c>0;③4a+2b+c>0;④2a+b=0;⑤b2>4ac.其中正确的结论有 个.
13.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:
x … ﹣1 0 1 4 …
y … 10 5 2 5 …
则当x≥1时,y的最小值是 .
14.已知M、N两点关于y轴对称,且点M在双曲线上,点N在直线y=﹣x+3上,设点M坐标为(a,b),则y=﹣abx2+(a+b)x的顶点坐标为 .
15.如图,正方形ABCD的边长为2,E为边AD上一动点,连接BE、CE,以CE为边向右侧作正方形CEFG.
(1)若BE=,则正方形CEFG的面积为 ;
(2)连接DF、DG,则△DFG面积的最小值为 .
16.已知矩形长与宽分别为a、b(a>b),截一个面积最大的菱形,使菱形的顶点落在矩形的边上,该菱形最大面积为 .
17.当﹣1≤x≤1时,函数y=﹣x2﹣2mx+2n+1的最小值是﹣4,最大值是0,则m、n的值分别是 .
18.在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(﹣2,6),C(2,2)两点.
(1)记抛物线顶点为D,求△BCD的面积;
(2)若直线y=﹣x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.
19.如图,函数y=﹣x+2的图象交y轴于M,交轴于N,点P是直线MN上任意一点,PQ⊥x轴,设Q是垂足,设点Q的坐标为(t,0),△POQ的面积为S(当点P与M、N重合时,其面积记为0).
(1)试求S与t之间的函数关系式;
(2)在如图所示的直角坐标系内画出这个函数的图象,并利用图象求使得s=a(a>0)的点P的个数.
20.在平面直角坐标系xOy中,直线y=x+1与y轴交于点A,并且经过点B(3,n).
(1)求点B的坐标;
(2)如果抛物线y=ax2﹣4ax+4a﹣1(a>0)与线段AB有唯一公共点,求a的取值范围.
21.如图,在矩形ABCD中,AB=3cm,BC=4cm.设P,Q分别为BD,BC上的动点,在点P自点D沿DB方向作匀速移动的同时,点Q自点B沿BC方向向点C作匀速移动,移动的速度均为1cm/s,设P,Q移动的时间为t秒(0<t≤4).
(1)写出△PBQ的面积S(cm2)与时间t(s)的函数关系式,当t为何值时,S有最大值,最大值是多少?
(2)当t为何值时,△PBQ为等腰三角形?
22.如图,已知抛物线y=x2+bx+c经过A(﹣1,0),B(3,0)两点.
(1)求b和c;
(2)当0<x<4时,求y的取值范围;
(3)点P为x轴下方抛物线上一点,试说明P点运动到哪个位置时S△PAB最大,并求出最大面积.
23.如图,在平面直角坐标系中,抛物线y=﹣x2﹣x+与直线y=x+b交于A、B两点,其中点A在x轴上,点P是直线AB上方的抛物线上一动点(不与点A、B重合)过P作y轴的平行线交直线于点C,连接PA、PB.
(1)求直线的解析式及A、B点的坐标;
(2)当△APB面积最大时,求点P的坐标以及最大面积.
参考答案
1.解:①观察图象可知:
a<0,b<0,c>0,∴abc>0,
所以①正确;
②当x=时,y=0,
即a+b+c=0,
∴a+2b+4c=0,
∴a+4c=﹣2b,
∴a﹣2b+4c=﹣4b>0,
所以②正确;
③因为对称轴x=﹣1,抛物线与x轴的交点(,0),
所以与x轴的另一个交点为(﹣,0),
当x=﹣时,a﹣b+c=0,
∴25a﹣10b+4c=0.
所以③正确;
④当x=时,a+2b+4c=0,
又对称轴:﹣=﹣1,
∴b=2a,a=b,
b+2b+4c=0,
∴b=﹣c.
∴3b+2c=﹣c+2c=﹣c<0,
∴3b+2c<0.
所以④错误.
或者∵当x=1时,a+b+c<0,
∴c<﹣a﹣b,
又∵b=2a,
∴a=b,
∴c<﹣b,
∴2c<﹣3b,
∴2c+3b<0,
∴结论④错误
故选:C.
2.解:∵抛物线开口向下,
∴a<0,
∵抛物线交y轴于正半轴,
∴c>0,
∵﹣>0,
∴b>0,
∴abc<0,故①正确,
∵x=﹣2时,y<0,
∴4a﹣2b+c<0,即4a+c<2b,故②正确,
∵y=ax2+bx+c的图象过点(﹣1,0)和(m,0),
∴﹣1×m=,am2+bm+c=0,
∴++=0,
∴=1﹣,故③正确,
∵﹣1+m=﹣,
∴﹣a+am=﹣b,
∴am=a﹣b,
∵am2+(2a+b)m+a+b+c
=am2+bm+c+2am+a+b
=2a﹣2b+a+b
=3a﹣b<0,故④正确,
∵m+1=|﹣|,
∴m+1=||,
∴|am+a|=,故⑤正确,
故选:B.
3.解:A.∵二次函数的图象开口向下,图象与y轴交于y轴的正半轴上,
∴a<0,c>0,
∵抛物线的对称轴是直线x=1,
∴﹣=1,
∴b=﹣2a>0,
∴abc<0,故本选项错误;
B.∵图象与x轴有两个交点,
∴b2﹣4ac>0,故本选项错误;
C.∵对称轴是直线x=1,与x轴一个交点是(﹣1,0),
∴与x轴另一个交点的坐标是(3,0),
把x=3代入二次函数y=ax2+bx+c(a≠0)得:y=9a+3b+c=0,故本选项错误;
D.∵当x=3时,y=0,
∵b=﹣2a,
∴y=ax2﹣2ax+c,
把x=4代入得:y=16a﹣8a+c=8a+c<0,
故选:D.
4.解:一次函数y=mx+n与x轴的轴交于点A,故点(a,0),
将点A(a,0)坐标代入一次函数表达式得:0=am+n,
解得:n=﹣am,
故一次函数的表达式为y=mx﹣am,
∵点B、C在一次函数上,故点B、C的坐标分别为(b,mb﹣ma)、(c,mc﹣ma),
设二次函数的表达式为y=Ax2,
点B、C在该二次函数上,则,
(1)②﹣①得:A(b2﹣c2)=m(c﹣b),等式两边同除以Ab2得,,即,故B正确,不符合题意;
(2)①÷②得:③,即C正确,不符合题意;
(3)化简③得:a=,即=,故D正确,不符合题意;
(4)化简A得:a2﹣c2=﹣bc﹣ab,化简得:a+b=c,而从上述各式看,该式不一定成立,故A符合题意,
故选:A.
5.解:如图,设C点关于抛物线对称轴的对称点为C′,由对称的性质可得CE=C′E,
∴CE+EF=C′E+EF,
∴当F、E、C′三点一线且C′F与AB垂直时CE+EF最小,
由题意可得,解得,
∴直线解析式为y=x+3;
∵C(0,1),
∴C′(2,1),
∴直线C′F的解析式为y=﹣x+,
由,解得,
∴F(,),
∴C′F==
即CE+EF的最小值为.
故选:C.
6.解:设过点P平行直线y1的解析式为y=x+b,
当直线y=x+b与抛物线只有一个交点时,点P到直线y1的距离最小,
由,消去y得到:x2﹣2x+2b=0,
当Δ=0时,4﹣8b=0,
∴b=,
∴直线的解析式为y=x+,
如图设直线y1交x轴于A,交y轴于B,直线y=x+交x轴于C,作CD⊥AB于D,PE⊥AB于E,则A(﹣3,0),B(0,3),C(﹣,0)
∴OA=OB=3,OC=,AC=,
∴∠DAC=45°,
∴CD==,
∵AB∥PC,CD⊥AB,PE⊥AB,
∴PE=CD=,
故选:B.
7.解:令y=0,得 (x﹣m)(x﹣m﹣3)=0,
解得x1=m,x2=m+3,
∴抛物线与x轴的两个交点为(m,0 )和(m+3,0),
∵抛物线经过四个象限,
∴(m,0 )和(m+3,0)分别位于原点两侧,
即 m<0<m+3,
∴﹣3<m<0,
故选:C.
8.解:如图,分别作AE、BF垂直于x轴于点E、F,
设OE=a,OF=b,由抛物线解析式为y=x2,
则AE=a2,BF=b2,
作AH⊥BF于H,交y轴于点G,连接AB交y轴于点D,
设点D(0,m),
∵DG∥BH,
∴△ADG∽△ABH,
∴,即.
化简得:m=ab.
∵∠AOB=90°,
∴∠AOE+∠BOF=90°,
又∠AOE+∠EAO=90°,
∴∠BOF=∠EAO,
又∠AEO=∠BFO=90°,
∴△AEO∽△OFB.
∴,
即,
化简得ab=1.
则m=ab=1,说明直线AB过定点D,D点坐标为(0,1).
∵∠DCO=90°,DO=1,
∴点C是在以DO为直径的圆上运动,
∴当点C到y轴距离为=时,点C到y轴距离的最大.
故选:A.
9.解:①∵图象与x轴的交点A,B的横坐标分别为﹣1,3,
∴AB=4,
∴对称轴x==1,
即2a+b=0;
故①正确;
②由抛物线的开口方向向上可推出a>0,而>0
∴b<0,
∵对称轴x=1,
∴当x=1时,y<0,
∴a+b+c<0;
故②错误;
③∵图象与x轴的交点A,B的横坐标分别为﹣1,3,
∴a﹣b+c=0,9a+3b+c=0,
∴10a+2b+2c=0,
∴5a+b+c=0,
∴a+4a+b+c=0,
∵a>0,
∴4a+b+c<0,
故③错误;
④要使△ABD为等腰直角三角形,必须保证D到x轴的距离等于AB长的一半;
D到x轴的距离就是当x=1时y的值的绝对值.
当x=1时,y=a+b+c,
即|a+b+c|=2,
∵当x=1时y<0,
∴a+b+c=﹣2,
又∵图象与x轴的交点A,B的横坐标分别为﹣1,3,
∴当x=﹣1时y=0即a﹣b+c=0;
x=3时y=0.
∴9a+3b+c=0,
解这三个方程可得:b=﹣1,a=,c=﹣;
⑤要使△ACB为等腰三角形,则必须保证AB=BC=4或AB=AC=4或AC=BC,
当AB=BC=4时,
∵AO=1,△BOC为直角三角形,
又∵OC的长即为|c|,
∴c2=16﹣9=7,
∵由抛物线与y轴的交点在y轴的负半轴上,
∴c=﹣,
与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=;
同理当AB=AC=4时,
∵AO=1,△AOC为直角三角形,
又∵OC的长即为|c|,
∴c2=16﹣1=15,
∵由抛物线与y轴的交点在y轴的负半轴上,
∴c=﹣
与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=;
同理当AC=BC时
在△AOC中,AC2=1+c2,
在△BOC中BC2=c2+9,
∵AC=BC,
∴1+c2=c2+9,此方程无解.
经解方程组可知只有两个a值满足条件.
故⑤错误.
故答案为:①④.
10.解:∵抛物线的开口向上,
∴a>0;
∵对称轴为x=<0,
∴a、b同号,即b>0.
∴一次函数y=ax+b的图象不经过第四象限.
11.解:设正方形OABC的边长为m,DE=n,CD=EF=2n,
∵点M为OC的中点,
∴点M为(0,m)、点B为(m,m)和点E为(2n,m+n),
∵抛物线y=ax2+b经过M,B,E三点,
∴m=am2+,
解得:a=,
∴抛物线y=x2+,
把点E(2n,m+n)代入抛物线得
m+n= 4n2+,
解得:m=(﹣1)n或m=(﹣﹣1)n不合题意,舍去),
∴==.
12.解:抛物线开口向下,因此a<0,对称轴为x=1>0,因此a、b异号,所以b>0,抛物线与y轴交点在正半轴,因此c>0,所以abc<0,于是①正确;
抛物线的对称轴为直线x=﹣=1,因此有2a+b=0,故④正确;
当x=﹣1时,y=a﹣b+c<0,而2a+b=0,所以3a+c<0,故②不正确;
抛物线与x轴有两个不同交点,因此b2﹣4ac>0,即b2>4ac,故⑤正确;
抛物线的对称轴为x=1,与x轴的一个交点在﹣1与0之间,因此另一个交点在2与3之间,于是当x=2时,y=4a+2b+c>0,因此③正确;
综上所述,正确的结论有:①③④⑤,
故答案为:4.
13.解:∵由表可知,当x=﹣1时,y=10,当x=0时,y=5,当x=1时,y=2,
∴,解得,
∴抛物线的解析式为y=x2﹣4x+5,
∴其对称轴为直线x=﹣=﹣=2.
∵x≥1,
∴当x=2时,y最小===1.
故答案为:1.
14.解:∵M、N两点关于y轴对称,
∴M坐标为(a,b),N为(﹣a,b),分别代入相应的函数中得,b=①,a+3=b②,∴ab=,(a+b)2=(a﹣b)2+4ab=11,a+b=±,
∴y=﹣x2±x,
∵=±,=,
∴顶点坐标(,)或(﹣,).
故答案为:(,)或(﹣,).
15.解:(1)∵四边形ABCD是正方形,
∴AB=AD=2,∠A=∠D=90°,
∵BE=,
∴AE===1,
∴DE=AD﹣AE=2﹣1=1,
∴EC2=DE2+CD2=12+22=5,
∴正方形CEFG的面积=EC2=5.
故答案为5;
(2)连接DF,DG.设DE=x,则CE=,
∵S△DEC+S△DFG=S正方形ECGF,
∴S△DFG=(x2+4)﹣×x×2
=x2﹣x+2
=(x﹣1)2+,
∵>0,
∴x=1时,△DFG的面积的最小值为.
故答案为.
16.解:∵菱形顶点都落在矩形边上,
∴菱形的高为b,
当底最长时菱形面积最大,
此时菱形两个顶点与矩形顶点重合,如图,
设BF=DF=x,则CF=a﹣x,
在Rt△CDF中,由勾股定理得:
FC2+CD2=DF2,
即(a﹣x)2+b2=x2,
解得x=,
∴S菱形BFDE=BF CD=.
故答案为:.
17.解:∵函数y=﹣x2﹣2mx+2n+1=﹣(x+m)2+m2+2n+1,
∴该函数图象开口向下,对称轴为直线x=﹣m,
∵当﹣1≤x≤1时,函数y=﹣x2﹣2mx+2n+1的最小值是﹣4,最大值是0,
∴当﹣m<﹣1时,m>1,当x=﹣1时,y=0,当x=1时,y=﹣4,
即,解得,不符合m>1,故此种情况不存在;
当﹣1≤﹣m≤1时,﹣1≤m≤1,x=﹣m时,y=0,当x=﹣1时y=﹣4或x=1时y=﹣4,
即或,
解得或;
当﹣m>1时,m<﹣1,当x=1时,y=0,x=﹣1时,y=﹣4,
即,
解得,不符合m<﹣1,故此种情况不存在;
由上可得,m、n的值分别是﹣1,﹣1或1,﹣1,
故答案为:﹣1,﹣1或1,﹣1.
18.解:(1)把B(﹣2,6),C(2,2)两点坐标代入得:,
解这个方程组,得 ,
∴抛物线的解析式为y=x2﹣x+2;
∵y=x2﹣x+2=(x﹣1)2+,
∴顶点D(1,),
∵B(﹣2,6),C(2,2),
∵直线BC为y=﹣x+4,
∴对称轴与BC的交点H(1,3),
∴S△BDC=S△BDH+S△DHC=×(3﹣) 3+×(3﹣) 1=3.
(2)由消去y得到x2﹣x+4﹣2b=0,
当Δ=0时,直线与抛物线相切,1﹣4(4﹣2b)=0,
∴b=,
当直线y=﹣x+b经过点C时,b=3,
当直线y=﹣x+b经过点B时,b=5,
∵直线y=﹣x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,
∴<b≤3.
19.解:(1)①当t<0时,OQ=﹣t,PQ=﹣t+2,
∴S= (﹣t)(﹣t+2)=t2﹣t;
②当0<t<4时,OQ=t,PQ=﹣t+2,
∴S= t(﹣t+2)=﹣t2+t;
③当t>4时,OQ=t,PQ=﹣(﹣t+2)=t﹣2,
∴S= t(t﹣2)=t2﹣t;
④当t=0或4时,S=0;
于是,S=;
(2)S=
下图中的实线部分就是所画的函数图象.
观察图象可知:
当0<a<1时,符合条件的点P有四个;
当a=1时,符合条件的点P有三个;
当a>1时,符合条件的点P只有两个.
20.解:(1)把x=3代入y=x+1,y=3+1=4,∴点B的坐标为B(3,4);
(2)由题意:线段ABy=x+1(0≤x≤3),
∵y=ax2﹣4ax+4a﹣1=a(x﹣2)2﹣1,
∴抛物线的对称轴为直线x=2,顶点坐标为(2,﹣1),
∵点A(0,1),点B(3,4),
∵当抛物线y=ax2﹣4ax+4a﹣1(a>0)与线段AB有唯一公共点时,
∴①或②
解①得≤a<5,②无解,
综上所述,当≤a<5时,抛物线与线段AB有一个公共点.
21.解:(1)矩形ABCD中,BD===5,
过点P作PM⊥BC,垂足为M,
∴△BPM∽△BDC
∴,
∴PM=(5﹣t),
∴S=t×(5﹣t)=﹣(t﹣)2+,
∴当t=时,S有最大值;
(3)①当BP=BQ时,5﹣t=t,
∴t=,
②当BQ=PQ时,作QE⊥BD,垂足为E,
此时,BE=BP=,
∴△BQE∽△BDC
∴即,
∴t=.
③当BP=PQ时,作PF⊥BC,垂足为F,
此时,BF==t,
∴△BPF∽△BDC
∴即,
∴t=.
∴t=或或均使△PBQ为等腰三角形.
22.解:(1)将点A(﹣1,0),B(3,0)代入抛物线y=x2+bx+c,
得,解得:;
(2)由(1)可知抛物线解析式为y=x2﹣2x﹣3=(x﹣1)2﹣4,即抛物线对称轴为x=1,
所以当x=1时,ymin=﹣4;当x=4时,ymax=5;
而由已知知:0<x<4,所以此时y的范围为﹣4≤y<5;
(3)当点P在抛物线顶点(1,﹣4)时S△PAB最大,
最大面积为S△PAB=AB |yP|=×4×4=8.
23.解:(1)∵y=﹣x2﹣x+,
∴当y=0时,﹣x2﹣x+=0,
解得x1=﹣,x2=1,
∴A点的坐标为(1,0).
将A(1,0)代入y=x+b,
得0=×1+b,
解得b=﹣,
∴直线的解析式为y=x﹣.
由,解得,,
∴B点的坐标为(﹣5,﹣3);
(2)设P(x,﹣x2﹣x+),则C(x,x﹣),
∴PC=(﹣x2﹣x+)﹣(x﹣)=﹣x2﹣4x+5,
∴S△APB=PC |xA﹣xB|
=(﹣x2﹣4x+5)×(1+5)
=﹣3x2﹣12x+15
=﹣3(x+2)2+27,
当x=﹣2时,△APB面积最大,最大值为27,此时点P的坐标为(﹣2,).
